Предыстория

Будучи студентом, я решил в качестве курсовой разработать бота для поиска цепочки друзей для соцсети. Мне это показалось достаточно интересным, начал поиск информации на эту тему. В итоге я наткнулся на статью о теория шести рукопожатий, там была описана идея двунаправленного поиска, что показалось мне самым лучшим решением для такой задачи. Вот только никакого алгоритма и его реализации я не обнаружил, поэтому решил разработать свой вариант алгоритма. Теперь же хочу поделиться алгоритмом, который мне удалось разработать.

Обозначения

(source) — id первого пользователя
(source friends) — список id друзей первого пользователя
(target) — id второго пользователя
(target friends) — список id друзей второго пользователя
(mutual friend) — самый дальний общий знакомый, т.е. расстояние от до и расстояние от до равны либо отличаются на 1

Алгоритм

0. Находим списки друзей дляии рассматриваем следующие варианты:
1*. Еслиили, то выводим цепочку
2*. Если, то выводим цепочку, где— любое id из
3*. Если не выполнено 1* и 2*, то переходим к шагу 1

1. Исследуем новый уровень друзей для, т.е. смотрим, где. Если находится такой, что, тогда и переходим к шагу 3, иначе
и переходим к шагу 2

2. Исследуем новый уровень друзей для, т.е. смотрим, где. Если находится такой, что, тогда и переходим к шагу 3, иначе
и переходим к шагу 1

3. Найден, тогда цепочка будет иметь вид. Рассмотрим подцепочки иПроделаем шаг 1 для пари,и. Тогда получимдля парыи,для парыи.

4. Найденыи, тогда цепочка будет иметь вид. Тогда проделаем шаг 1 для пар и,и,и,и. Тогда получим для парыи,для парыи,для парыи,для парыи.

5. Найдены ,,,, тогда цепочка будет иметь вид .
Проделаем шаг 1 для пари,...,и.

И т.д. пока все новые, найденные на -ом шаге, не станут равны .

Графическая интерпретация алгоритма

Шаг 0 (Находим списки друзей дляи)

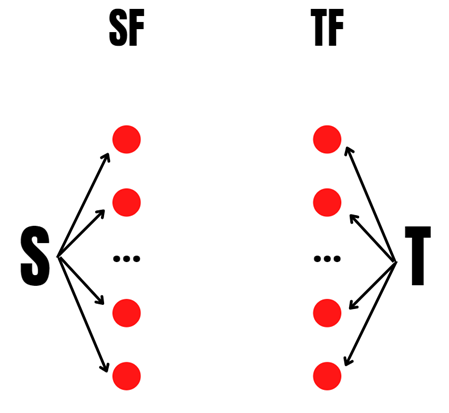
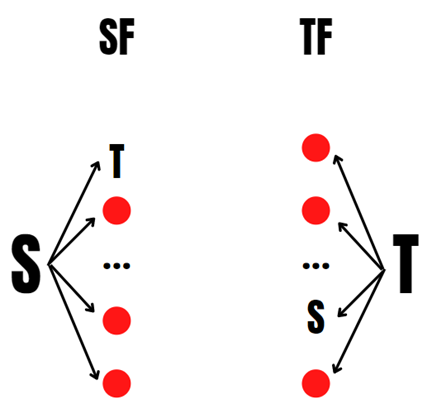
Шаг 0.1* (Еслиили )

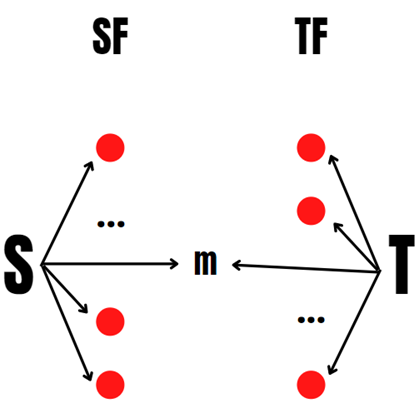
Шаг 0.2* (Если )

Шаг 0.3* (Не выполнены шаги 1* и 2*, значит переходим к шагу 1)

Шаг 1

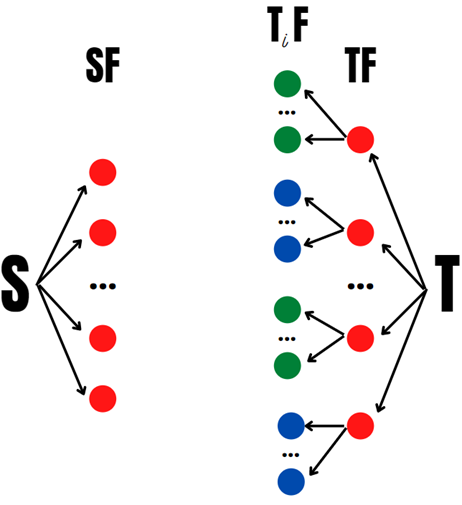
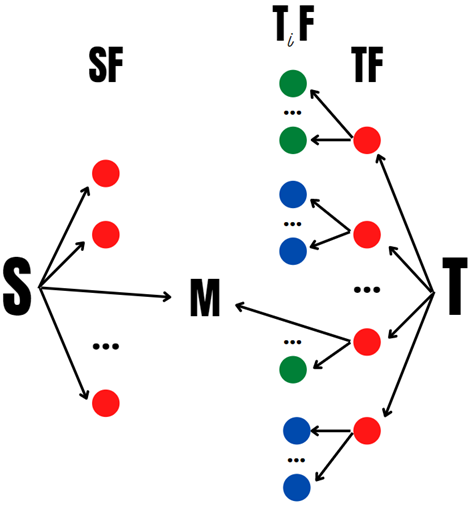
Шаг 2

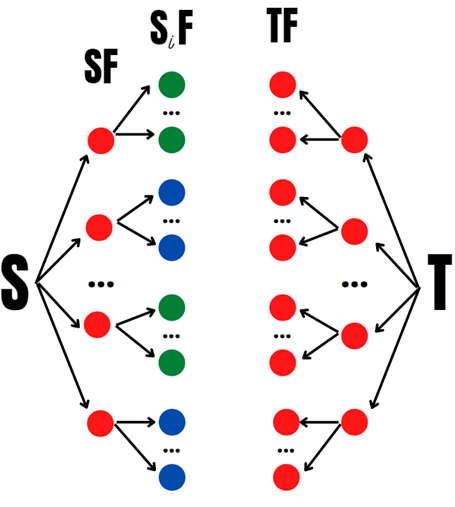
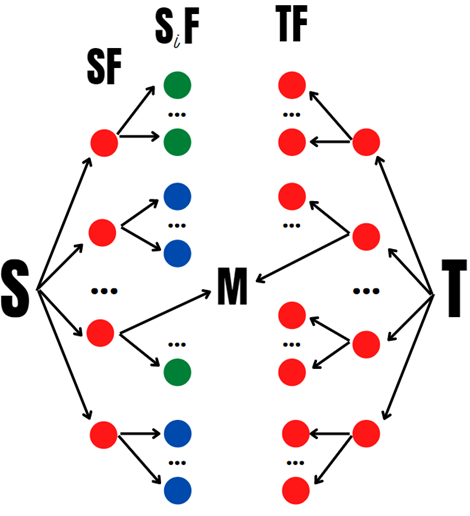
Шаг 2 Шаг 1 (Для наглядности посмотрим, что происходит при переходе с шага 2 на шаг 1)

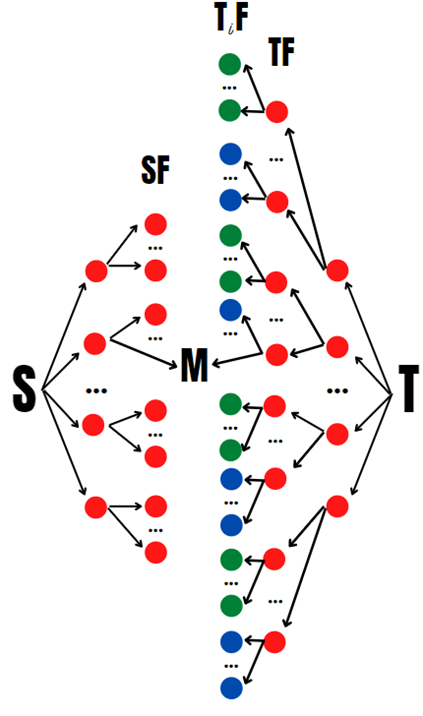
Шаг 3 (. Проделаем шаг 1 для пари, и)

Параи

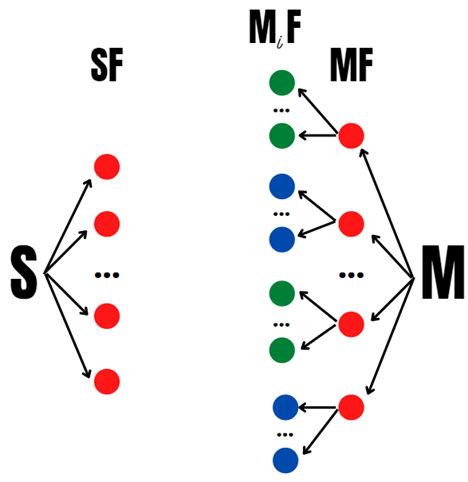
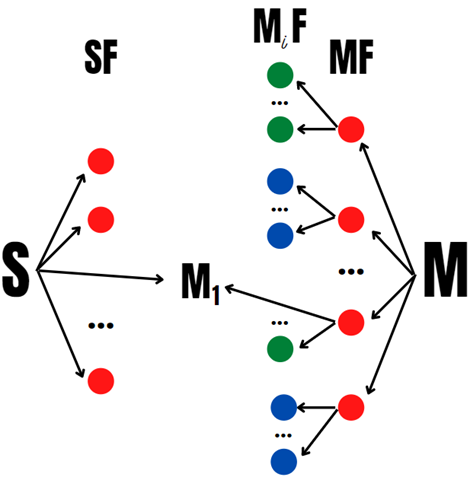
Параи

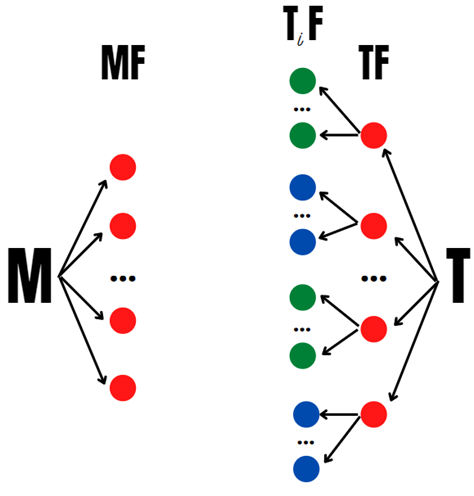
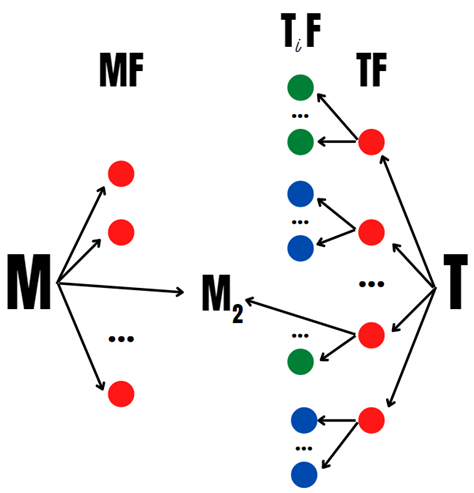
Последующие шаги понятны, поэтому в графической интерпретации не нуждаются.

Замечание

Если посмотреть на шаги, на которых находим, то можно заметить момент, который оптимизирует алгоритм. Когда проходим по-ому другу изи находим для его спискапересечение c, то можно возвращать не только, но и этого
-ого друга. Таким образом, за каждую итерацию находим 2 последовательных элемента цепочки, т.е. вместополучаемлибо.

Реализация

Функция для поиска

# source и target - id пользователей S и T
# limit - флаг ограничения по количеству проверяемых пользователей в списках друзей 
def find_mutual_friend(source, target, limit=False):
	# Ограничение по количеству проверяемых пользователей в списках друзей
    FRIENDS_COUNT = 100

	if source == target:
		return None, None, None

	if None in [source, target]:
		return None, None, None

    # Получаем списки друзей для S и T
	source_friends = get_friends(source)
	target_friends = get_friends(target)

	if source in target_friends or target in source_friends:
		return None, None, None
	
	mutual_friends = intersection(source_friends, target_friends)
	if mutual_friends:
		return None, None, mutual_friends[0]

	source_friends = get_friends(source) if not limit else get_friends(source, count=FRIENDS_COUNT)
	target_friends = get_friends(target) if not limit else get_friends(target, count=FRIENDS_COUNT)

	# 0 - достраиваем уровень друзей для T
	# 1 - достраиваем уровень друзей для S
	i = 0
	last_source_level = source_friends
	last_target_level = target_friends
	while True:
        # Обновление SF как более глубокий уровень друзей для S
		if i:
			next_source_level = []

			for friend in last_source_level:
				friends = get_friends(friend, count=FRIENDS_COUNT)
				if not friends:
					continue
				mutual_friends = intersection(last_target_level, friends)					
				
				if mutual_friends:
					return i, friend, mutual_friends[0]

				next_source_level = union(next_source_level, friends)
				
			last_source_level = next_source_level
			i = 0
			continue

        # Обновление TF как более глубокий уровень друзей для T
		next_target_level = []

		for friend in last_target_level:
			friends = get_friends(friend, count=FRIENDS_COUNT)
			if not friends:
				continue
			mutual_friends = intersection(last_source_level, friends)

			if mutual_friends:
				return i, friend, mutual_friends[0]
					
			next_target_level = union(next_target_level, friends)
				
		last_target_level = next_target_level
		i = 1

Функция для формирования цепочки друзей дляи

# source и target - id пользователей S и T
def create_chain(source, target):
    # Шаг 0
    # Получаем списки друзей для S и T
	source_friends = get_friends(source)
	target_friends = get_friends(target)

    # Если |TF| > |SF|, то лучше поменять пользователей S и T местами
    # Это связано с тем, что в алгоритме поиск начинается с пользователя T
	if len(target_friends) > len(source_friends):
		temp = source
		source = target
		target = temp

    # Находим M и m (про это описано в замечании)
    # i - указатель стороны, с которой находится пользователь m
    # friend - m
    # mutual_friend - M
	i, friend, mutual_friend = find_mutual_friend(source, target)

    # Шаг 0.1
    # Пользователи S и T являются друзьями 
	if mutual_friend is None:
		return [source, target]

	chain = [source, mutual_friend, target]

    # Шаг 0.2
    # Нет пользователя m, значит возаращаем цепочку [S, M, T]
	if not friend:
		return chain

    # Шаг 0.3
    # Определяем начальную цепочку, которую будет достраивать
	chain = [source, friend, mutual_friend, target] if i else [source, mutual_friend, friend, target]
	while True:
		new_chain = []
		new_mutual_friends = []

        # Находим M и m для пар пользователей из уже составленной цепочки
		for i in range(len(chain) - 1):
			j, friend, mutual_friend = find_mutual_friend(chain[i], chain[i + 1], limit=True)

			new_mutual_friends.append(mutual_friend)

            # Составление подцепочки в формате [S, M, T], либо [S, M, m, T], либо [S, m, M, T] 
			new_chain.append(chain[i])
			if friend not in chain:
				if j:
					new_chain += [friend, mutual_friend]
				else:
					new_chain += [mutual_friend, friend]
			else:
				if mutual_friend:
					new_chain.append(mutual_friend)

        # Дополняем цепочку новыми промежуточными пользователями
		chain = new_chain + [chain[-1]]

        # Проверка на то, что все новые M являются None
		if new_mutual_friends.count(None) == len(new_mutual_friends):
			break

    # Избавляемся от значений None в итоговой цепочке
    # None появляется как M для некоторой пары пользователей, которые являются друзьями
	return remove_None(chain)

Заключение

Алгоритм получился достаточно интересным, но его ещё можно улучшить. Он не является оптимальным, т.к. находит хотя бы какую-то цепочку друзей. Также пользователи могут встречаться не один раз, что приводит к выполнению лишних проверок.

Надеюсь, что данная статья будет кому-нибудь полезна, и жду предложений по оптимизации в комментариях.