
Сегодняшние задачки посвящены победе Аргентины на ЧМ по футболу. Их создатель – Родолфо Курчан, всемирно известный изобретатель головоломок и автор из Буэнос-Айреса.
1. Математика от Месси
Замените буквы в нижеприведённой сумме цифрами от 0 до 9 так, чтобы пример был верным. Каждая буква соответствует уникальной цифре. У задачки есть два решения – найдите то, сумма в котором наибольшая.

Решение
92335 + 92335 = 184670
(Второе решение: 52339 + 52339 = 104678)
Один из способов найти решение следующий. Мы ищем наибольший возможный результат для Messi. Допустим, M = 9. Тогда F = 1 и U = 8. E + E должно быть меньше 10 (переноса нет), поэтому E = 0, 2, 3 или 4. E не может равняться 0, поскольку тогда T равнялось бы 0 или 1 – а это невозможно. E также не может равняться 4, поскольку тогда T равнялось бы 8 или 9, что тоже невозможно. Получается, E = 2 или 3.
S не может быть 0, поскольку тогда O или B тоже 0. Не может быть нулём и I, поскольку тогда L тоже должна быть нулём. Не может быть нулём и T, поскольку тогда пришлось бы делать перенос в столбец M. B и O тоже не могут быть нулём – тогда S=5, но этого не может быть, поскольку тогда B=1, а 1 уже занята. Тогда L = 0, а следовательно I = 5.
Мы знаем, что E = 2 или 3. Допустим, E = 3. Тогда T = 6 или 7. Если T = 6, тогда 2, 4 и 7 никак не получится распределить по оставшимся буквам. Не получится это и в случае, когда T = 7. Поэтому E не равно 3.
Допустим, E = 2. Тогда T = 4, и тогда мы финишируем, так же красиво, как Месси, с S = 3, O = 7 и B = 6.
(Второе решение: 52339 + 52339 = 104678)
Один из способов найти решение следующий. Мы ищем наибольший возможный результат для Messi. Допустим, M = 9. Тогда F = 1 и U = 8. E + E должно быть меньше 10 (переноса нет), поэтому E = 0, 2, 3 или 4. E не может равняться 0, поскольку тогда T равнялось бы 0 или 1 – а это невозможно. E также не может равняться 4, поскольку тогда T равнялось бы 8 или 9, что тоже невозможно. Получается, E = 2 или 3.
S не может быть 0, поскольку тогда O или B тоже 0. Не может быть нулём и I, поскольку тогда L тоже должна быть нулём. Не может быть нулём и T, поскольку тогда пришлось бы делать перенос в столбец M. B и O тоже не могут быть нулём – тогда S=5, но этого не может быть, поскольку тогда B=1, а 1 уже занята. Тогда L = 0, а следовательно I = 5.
Мы знаем, что E = 2 или 3. Допустим, E = 3. Тогда T = 6 или 7. Если T = 6, тогда 2, 4 и 7 никак не получится распределить по оставшимся буквам. Не получится это и в случае, когда T = 7. Поэтому E не равно 3.
Допустим, E = 2. Тогда T = 4, и тогда мы финишируем, так же красиво, как Месси, с S = 3, O = 7 и B = 6.
2. Игра в четыре части
В каждой из пяти подзадач нужно разделить квадрат на четыре части одинаковой формы, размер которых определяется следующими утверждениями:
1) Все четыре части одного размера.
2) Только три части имеют один размер.
3) У двух частей один размер, а у двух оставшихся тоже одинаковый размер (но не такой, как у первых двух).
4) Две части одного размера, а оставшиеся две – разных размеров.
5) Все части имеют разный размер.
Первая подзадача решается так: делим квадрат на четыре треугольника – одной формы и одного размера.

Уточнение: в каждой из подзадач все части должны иметь одну форму, меняется только размер. Но в разных подзадачах могут быть части разного размера. Одно решение хорошо ложится на сетку 12х12, одно на сетку 10х10, а в одном используются треугольники. Подзадача 5) самая сложная.
Решение
Задачи 2) и 3)
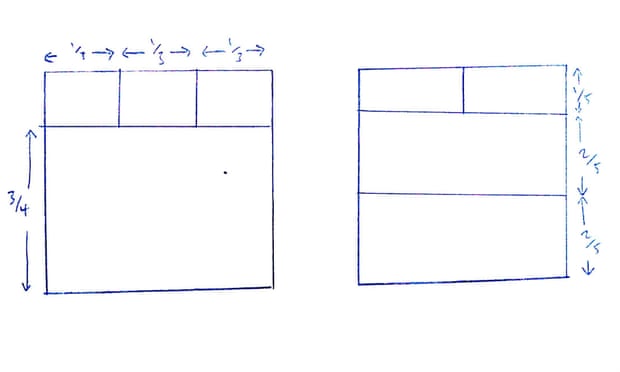
Левое решение укладывается на сетку 12х12, поскольку одну сторону нужно поделить на 4, а другую на 3. Правое укладывается на 10х10, потому что одну сторону надо поделить на 5, а другую на 2.
Задачи 4) и 5)

Пятое решение обнаружил Пабло Милруд

Левое решение укладывается на сетку 12х12, поскольку одну сторону нужно поделить на 4, а другую на 3. Правое укладывается на 10х10, потому что одну сторону надо поделить на 5, а другую на 2.
Задачи 4) и 5)

Пятое решение обнаружил Пабло Милруд
3. Змейки
В этой задаче нужно построить путь на решётке размера 5х5 из цифр, которые растут от 1 до 5, а потом начинают опять с 1 – и так по кругу. Путь может начинаться с любой клетки и двигаться только по горизонтали и вертикали. Он не может идти по диагонали или пересекать себя. На одной вертикали или горизонтали не может быть двух одинаковых цифр (как в судоку). Вот пример пути длиной 12 клеток:

Змейка закончилась, потому что 3 нельзя поставить ни в одну клетку, не нарушив запрета на повтор цифр в одной колонке и в одной строке.
Задача: найдите путь длиной 19 клеток – максимально возможный при таких условиях.
Задача со звёздочкой: какой самый длинный путь возможен на решётке 7х7 клеток, цифры в котором начинаются с 1, растут до 7, и потом опять идут с 1, по кругу?
Решение

Один из способов построения пути на решётке 5х5

Самый длинный путь на решётке 7х7 длиной в 39 клеток

Один из способов построения пути на решётке 5х5

Самый длинный путь на решётке 7х7 длиной в 39 клеток


OlegIva
В 5 решении для игры в 4 части там 6 или b? Если это 6, то, очевидно, стороны у квадрата получаются неравные. Значит это b. Тогда задача не доведена до решения, пока это самое b не вычислено.