Подбор гиперпараметров модели – одна из самых распространенных задач в data science. Если заранее неизвестно, какими могут быть оптимальные значения, приходится искать по сетке значений. Если у нас есть m гиперпараметров и для каждого задано n возможных значений, то число вариантов равно mn и для каждого нужно обучить модель и определить ее точность. Если мы используем перекрестную проверку (cross-validation), то это число надо умножить на число частей, на которые мы разбиваем набор данных.

Есть ряд алгоритмов оптимизации поиска, например байесовский – «осмысленный» поиск, при котором рассматриваются не все возможные сочетания гиперпараметров.

Относительно недавно sklearn был реализован еще один метод – halving search.

Ссылка

Метод реализован для регрессии и классификации. Принцип работы обоих вариантов одинаков.

Halving здесь означает «уполовинивание», т.е. деление на две части, хотя на практике используется деление на произвольное число частей (чаще всего на три).

Ниже модели с разными наборами гиперпараметров будем называть «кандидатами».

Идея в том, что проверку можно ускорить, уменьшив число объектов в учебном наборе данных. Однако при этом снижается точность прогноза, поэтому для окончательного отбора кандидатов лучше использовать все имеющиеся данные. Метод основан на следующем предположении:

Предположение: совсем плохих кандидатов можно отсеять, используя только часть выборки.

Видна аналогия с соревнованиями по кубковой системе. В начале участников много и задания не очень сложные. На первом раунде отсеиваются самые слабые. Потом задания усложняются и т.д., пока в финал не выйдут самые сильные, которые будут соревноваться на самых сложных заданиях.

Так же и в данном методе. Главный параметр алгоритма – factor, что можно перевести на русский как кратность (изменения числа кандидатов и размера выборки).

В первом раунде делается обычный поиск по сетке (grid search) для всех кандидатов, но на уменьшенной выборке (ее размер задает параметр min_resorces). На следующем раунде алгоритм уменьшает количество кандидатов в factor раз и увеличивает размер в выборки тоже в тоже число раз. Если все спланировать правильно, то на последней итерации будет использована (почти) вся выборка и число оставшихся кандидатов будет не больше кратности. Т.е. если кратность = 3, то в финале останется два или три кандидата.

Количество кандидатов алгоритм рассчитывает исходя из сетки параметров (param_grid), которую мы задаем так же как в обычном GridSearchCV.

Исходное значение размера выборки для первой итерации задает параметр min_resources.

Важно! Исходный размер выборки и кратность должны быть увязаны друг с другом и с размером полной выборки, чтобы на последней итерации была использована вся выборка и число кандидатов было не больше кратности. Иначе может получиться так, что достигнут полный размер выборки, а число кандидатов все еще больше кратности. Это не так страшно, просто на последней итерации будет много кандидатов, т.е. время работы алгоритма сократится не так сильно, как могло бы. Может получиться и наоборот: на последней итерации число кандидатов будет оптимальным, но размер выборки будет в разы меньше полного, что гораздо хуже.

Минимальный размер выборки можно и не задавать, например указав min_resources='exhaust'. Тогда алгоритм сам подберет мин. размер так, чтобы на последней итерации получилось оптимальное сочетание.

Единственная возможная проблем здесь в том, что тогда на первой итерации будет слишком маленький размер выборки, для того чтобы сравнение кандидатов давало надежные результаты (или вообще рассчитанный размер выборки будет меньше единицы). В этом случае можно задать параметр aggressive_elimination=True и указать некоторый разумный минимальный размер выборки. Тогда на первых нескольких итерациях будет использован этот минимальный размер, пока размер, рассчитанный алгоритмом, не превысит это значение.

Пример. Полный размер выборки 14580 элементов. Задаем min_resources=1620.

Расчет размеров выборки по итерациям:

Минимальный размер выборки, рассчитанный алгоритмом для первой итерации, 20, но это слишком мало. Однако, поскольку мы задали aggressive_elimination=True и min_resources=1620, вплоть до 4-й итерации будет использовано значение 1620, и только потом оно будет расти, каждый раз увеличиваясь путем умножения на кратность.

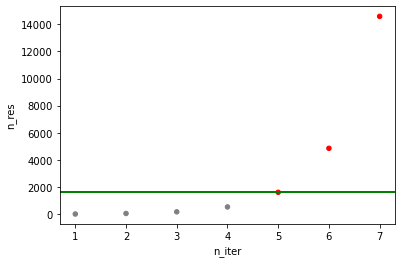
Важное замечание: размер выборки, используемой на последней итерации всегда кратен min_resources!

Например, у меня был набор данных размером 42100 объектов. Если задать мин. размер 2000 и кратность 3, то итоге на последней итерации алгоритм будет использовать всего 18000 объектов, т.е. меньше половины выборки (2000 * 3 = 6000; 6000 * 3 = 18000).

В этом случае можно изменить мин. размер на 5262 и кратность на 2, тогда на последней итерации будут использованы почти все объекты – 42096. Также можно задать мин. размер 4677 и кратность 3 (42093 на последней итерации).

Получается, при делении на учебную и валидационную выборки (train_test_split) лучше подбирать размер учебной выборки под кратность и размер минимальной выборки.

Еще одно замечание. Выше в качестве параметра, определявшего сложность каждого раунда «соревнования» между кандидатами, был использован размер выборки. Однако можно использовать и другой параметр (в этом алгоритме его называют «ресурс»), например число деревьев (n_estimators) случайного леса. Для этого указываем resource=n_estimators (по умолчанию число элементов – n_samples).

Прочие параметры аналогичны алгоритму GridSearchCV.

Сравнение с обычным поиском по сетке

Для сравнения был использован набор данных по отмене бронирования в гостиницах из соревнования на Kaggle (https://www.kaggle.com/competitions/playground-series-s3e7).

Классификатор – xgoost.

Метрика – ROC AUC на кросс-валидации (cv=5).

Для корректности сравнения во всех случаях в классификаторе задавал n_jobs=-1, в алгоритмах поиска n_jobs=1. GPU не использовал.

Сетка гиперпараметров логарифмическая, за исключением max_depth.

Команда для задания сетки:

params = {

    'n_estimators': np.logspace(1, 3, num=5, endpoint=True, base=10.0, dtype=int).tolist(),

    'max_depth': [2, 3, 4, 5],

    'learning_rate': np.logspace(-1, 0, num=5, endpoint=True, base=10.0).tolist(),

    'reg_alpha': np.logspace(-4, 0, num=5, endpoint=True, base=10.0).tolist(),

    'reg_lambda': np.logspace(-4, 0, num=5, endpoint=True, base=10.0).tolist()

}

В итоге имеем

{'n_estimators': [10, 31, 100, 316, 1000],

 'max_depth': [2, 3, 4, 5],

 'learning_rate': [0.1,

  0.1778279410038923,

  0.31622776601683794,

  0.5623413251903491,

  1.0],

 'reg_alpha': [0.0001, 0.001, 0.01, 0.1, 1.0],

 'reg_lambda': [0.0001, 0.001, 0.01, 0.1, 1.0]}

GridSearchCV

Обычный поиск по сетке с помощью функции GridSearchCV из библиотеки sklearn завершился за 5 часов 55 минут с результатом ROC AUC=0.8996.

Halving Search

Функция HalvingGridSearchCV тоже из sklearn.

Главный риск – упустить наилучший набор гиперпараметров на начальном этапе, из-за того что выборка слишком маленькая, поэтому важно осторожно выбирать min_resources.

При кратности 3 и min_resources=4677 поиск завершился за 1 час 6 минут с результатом чуть хуже, чем у «полного» поиска – 0.8887.

Если уменьшить начальный размер выборки до 1559 время поиска сокращается в два раза – до 30 мин. Площадь под кривой уменьшилась незначительно – до 0.8827.

Сравнение с другими алгоритмами

Сравнение с Optuna и т.п. не проводил, так как это инструменты другого уровня.

Напрашивается сравнение с байесовским поиском, хотя при использовании байесовских алгоритмов пользователь сам регулирует время поиска, задавая число итераций: чем больше число итераций, тем дольше поиск, но, скорее всего, выше достигнутая точность (заранее, однако, неизвестно, сколько именно потребуется итераций). Можно попробовать сравнить время, необходимое для достижения аналогичного уровня точности.

Испльзовал BayesSearchCV из библиотеки scopt. Пространство гиперпараметров:

space = {

    'n_estimators': Integer(10, 10000, prior='log-uniform', base=10),

    'max_depth': Integer(2, 5, prior='uniform'),

    'learning_rate': Real(1e-1, 1, prior='log-uniform', base=10),

    'reg_alpha': Real(1e-4, 1, prior='log-uniform', base=10),

    'reg_lambda': Real(1e-4, 1, prior='log-uniform', base=10)

}

На 100 итераций потребовался 1 час 22 мин. ROC AUC = 0.8994.

Ноутбук со сравнением выложен по ссылке.