Задача проверки корневых (под)деревьев на изоморфизм является достаточно известной в рамках олимпиадного мира, однако представленная большинством авторов реализация основывается на неэффективном полиномиальном хэшировании. Проблема данного метода заключается в возможных возникновениях коллизий. Согласно парадоксу дней рождений нам достаточно sqrt(mod) вершин, чтобы добиться вероятности коллизии в 50%. В данной статье описан более простой метод, использующий красно-черное дерево (в народе std::map) за ту же асимптотику.

Что такое изоморфизм графов?

Изоморфизм - логико-математическое понятие, выражающее одинаковость строения графов. Графы считаются изоморфными в том случае, если они имеют одинаковую структуру, но различный внешний вид - нумерацию вершин. Например, приведенные ниже графы изоморфны, и это несложно доказать:

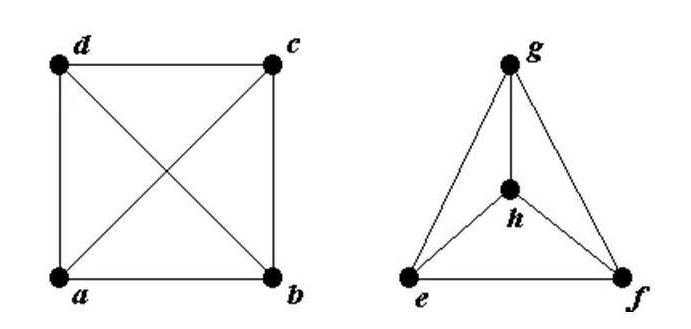
Насколько мне известно, решение задачи о проверке двух произвольных графов на изоморфизм за полиномиальное на данный момент является неизвестным. Несмотря на это, до сих пор не доказано, является ли она NP-полной.

Изоморфизм корневых деревьев

Для графов-деревьев существует эффективное решение, работающее за O(nlogn). Более того, оно легко модифицируется для проверки изоморфности поддеревьев за ту же асимптотику.

Обозначим n - размер деревьев (не берем в расчет случаи, когда размеры различны), r1 - корень первого дерева, r2 - корень второго дерева. Предположим, что деревья изначально изоморфны, следовательно, вершина r1 однозначно переходит в r2. Осталось лишь проверить соответственность детей данных вершин. Если существует отображение множества детей вершины r1 в r2, то наши деревья действительно изоморфны. Благодаря данному утверждению у нас появляется прекрасная возможность создания рекурсивного алгоритма:

1. Запускаемся из некоторой вершины v. Изначально v - корень дерева.

2. Проходимся по всем детям и получаем их хеш. Делаем это с помощью рекурсивного вызова исходной функции. Хешом в данном случае будем называть уникальный номер, характеризующий строение всех поддеревьев вершины.

3. На базе хешей детей получим хеш текущей вершины.

4. Сравним hash(r1) и hash(r2). Результат сравнения - изоморфность деревьев в данных корнях.

А как считать хеш?

Вместо того, чтобы использовать полиномиальное хеширование, описанное в статье на Алгоритмике, существует более простая эвристика. Для каждой вершины будем хранить множество хешей всех его непосредственных детей. Очевидно, что у изоморфных поддеревьев с корнями в вершинах v и u справедливо: hash(v) = hash(u). Поэтому просто будем хранить все существующие в дереве множества хешей детей и их уникальный номер. Для этого хорошо подходит структура данных std::map, осуществляющая все необходимые операции за O(logn).

Итоговый псевдокод

map<vector<int>, int> hashes;
vector<int> hsh_v;

int getHash(vector<int>& v) {
    if (hashes.find(v) == hashes.end())
        hashes[v] = (int)hashes.size();
    return hashes[v];
}

int dfs(int v, int p, graph& g) {
    vector<int> children;
    for (auto u : g[v]) {
        if (u != p) children.pb(dfs(u, v, g));
    }
    sort(all(children));
    return hsh_v[v] = getHash(children);
}

void solve() {
    int n;
    cin >> n;
    int r1, r2;
    cin >> r1 >> r2;
    graph g1(n + 1), g2(n + 1);
    forn(i, 0, n - 1) {
        int v, u;
        cin >> v >> u;
        make_edge(v, u, g1);
    }
    forn(i, 0, n - 1) {
        int v, u;
        cin >> v >> u;
        make_edge(v, u, g2);
    }

    hashes.clear();
    hsh_v.assign(n + 1, -1);
    int h1 = dfs(r1, -1, g1);
    hashes.clear();
    hsh_v.assign(n + 1, -1);
    int h2 = dfs(r2, -1, g2);
    
    cout << (h1 == h2 ? "YES" : "NO");
}

Массив hsh_v необходим для проверки поддеревьев на изоморфизм. Это можно применить, например в этой задаче.

Так как суммарная длина всех векторов O(n), то асимптотика O(nlogn).

А что если корни неизвестны?

Поскольку изоморфные деревья различаются исключительно порядком нумерации вершин, центроидные вершины не меняются. Центроидом дерева называется такая вершина v, что если подвесить дерево за эту вершину, то размер поддеревьев всех её сыновей будет не больше n/2. Можно доказать, что в каждом дереве не больше двух центроидов. Следовательно, нам достаточно найти центроиды первого дерева - c1 и второго - c2, а затем запустить вышеописанный алгоритм на каждой паре вершин. Деревья изоморфны, если хотя бы в одном из запусков был получен результат YES. Алгоритм поиска центроидов дерева хорошо описан в следующей статье.

Примеры задач для практики

• https://codeforces.com/contest/1800/problem/G

• https://www.eolymp.com/ru/problems/3680 (из России работает только с VPN)

• https://codeforces.com/contest/763/problem/D

• https://open.kattis.com/problems/twochartsbecomeone

Литература

• https://ru.wikipedia.org/wiki/Изоморфизм_графов

• Tinkoff generation - https://youtu.be/fF-27yUEuvA

• https://codeforces.com/blog/entry/113465