Цефеиды

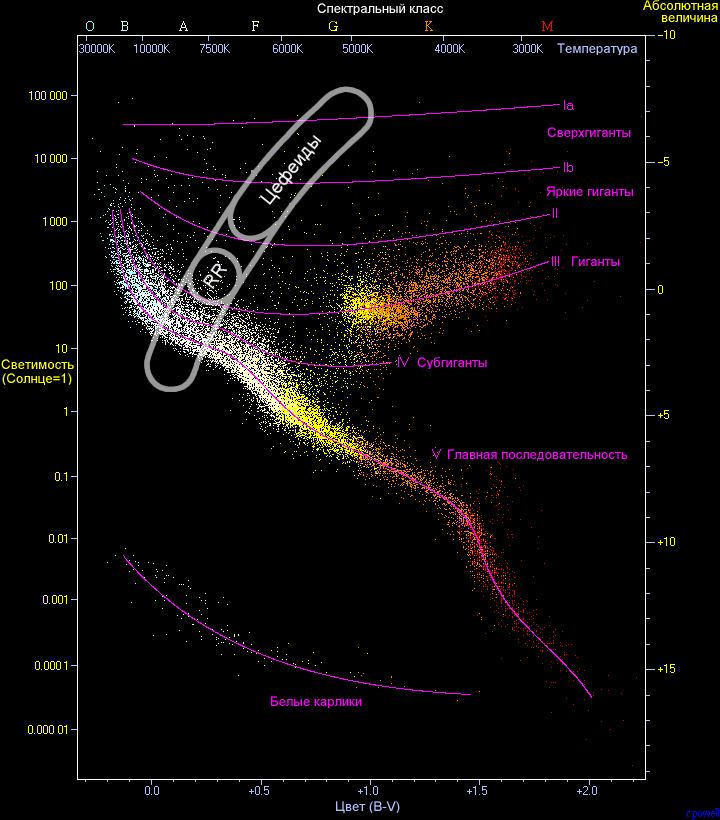
Переменная цефеида — это тип меняющей яркость звезды, пульсирующей радиально, и изменяющей как свой диаметр, так и температуру. При этом яркость звезды меняется с чётко определённым стабильным периодом и на определённую величину.

Цефеиды служат важными космическими ориентирами для определения галактических и межгалактических расстояний. Это возможно благодаря тому, что между светимостью переменной цефеиды и периодом её пульсации существует чёткая прямая зависимость. А зная собственную яркость объекта, можно вычислить расстояние до него, поскольку яркость убывает по закону обратных квадратов. В результате цефеиды служат т.н. «стандартными свечами».

10 сентября 1784 года английский астроном Эдвард Пиготт обнаружил, что тройная звезда Эта Орла меняет свою яркость. Она стала первым представителем класса классических переменных цефеид. Несколько месяцев спустя английский астроном-любитель Джон Гудрик обнаружил переменность, давшей этому классу название звезды Дельта Цефея. К концу XIX века число известных подобных переменных звёзд выросло до нескольких десятков, и их стали называть цефеидами. Большинство цефеид были известны по характерным формам кривой блеска с быстрым увеличением яркости и горбом на графике, а некоторые звёзды, с более симметричными кривыми блеска, называли геминидами по имени прототипа, Дзеты Близнецов.

Связь между периодом и светимостью для классических цефеид обнаружила в 1908 году Генриетта Суон Ливитт в ходе исследования тысяч переменных звёзд в Магеллановых Облаках. Она работала в обсерватории Гарвардского колледжа на должности ассистента профессора астрономии Эдуарда Чарльза Пикеринга, а также выполняла обязанности вычислителя. Опубликовала свою работу она в 1912 году с вместе дополнительными доказательствами. Она обнаружила, что у переменных Цефеид изменение радиальной скорости происходит с тем же периодом, что и изменение светимости. Первоначально это интерпретировали как доказательство того, что эти звезды — часть двойной системы. Однако в 1914 году Харлоу Шепли показал, что от этой идеи следует отказаться. Два года спустя Шепли и другие исследователи обнаружили, что переменные Цефеиды меняют свои спектральные типы в течение цикла.

В 1913 году Эйнар Герцшпрунг попытался найти расстояния до 13 цефеид, используя их движение по небу (впоследствии полученные им результаты пришлось пересмотреть). В 1918 году Харлоу Шепли использовал цефеиды, чтобы наложить первоначальные ограничения на размер и форму Млечного Пути и на расположение Солнца в нем. В 1924 году Эдвин Хаббл определил расстояние до классических переменных цефеид в галактике Андромеды, до тех пор известной как «Туманность Андромеды», и показал, что эти переменные звёзды лежат за пределами Млечного Пути. Выводы Хаббла разрешили вопрос, поднятый в «Великих дебатах» о том, представляет ли Млечный Путь всю Вселенную или является лишь одной из многих галактик во Вселенной.

В 1929 году Хаббл и Милтон Л. Хьюмасон сформулировали эмпирическое правило, известное сегодня как закон Хаббла, объединив расстояния между цефеидами и несколькими галактиками с измерениями скоростей, с которыми эти галактики удаляются от нас (измерения эти проводил Весто Мелвин Слайфер). Они обнаружили, что Вселенная расширяется, подтвердив тем самым теории Жоржа Леметра.

В середине 20 века значительные проблемы со шкалой астрономических расстояний были решены путём разделения цефеид на различные классы с очень разными свойствами. В 1940-х годах Уолтер Бааде понял, что существуют две отдельные популяции цефеид (классические и типа II). Классические цефеиды — это более молодые и массивные звезды популяции I, тогда как цефеиды типа II — это более старые и тусклые звезды популяции II. Они отличаются друг от друга зависимостями между периодом и светимостью.

Светимость цефеид II типа в среднем меньше, чем классических цефеид, примерно на 1,5 звёздной величины. Важнейшее открытие Бааде привело к двукратному увеличению оценки расстояния до М31 и внегалактической шкалы расстояний в целом.

Принятое объяснение механизма пульсации цефеид называется клапаном Эддингтона, или "κ-механизмом", где греческая буква κ (каппа) – обычное обозначение непрозрачности газа. Считается, что основным движителем этого процесса служит гелий. Дважды ионизированный гелий (гелий, в атомах которого отсутствуют оба электрона) более непрозрачен, чем однократно ионизированный гелий. Чем сильнее нагревается гелий, тем более ионизированным он становится. В самой тусклой части цикла Цефеиды ионизированный газ во внешних слоях звезды непрозрачен, поэтому он нагревается излучением звезды и из-за повышения температуры начинает расширяться. По мере расширения он охлаждается и становится менее ионизированным и, следовательно, более прозрачным, что позволяет излучению выходить наружу. Затем расширение останавливается, и под действием гравитационного притяжения звезды происходит обратное движение. После этого процесс повторяется.

Червоточины

Червоточина — это гипотетический туннель, соединяющий удалённые точки пространства-времени. Её существование можно теоретически вывести на основании специального решения уравнений поля Эйнштейна.

Червоточины согласуются с общей теорией относительности, но существуют ли червоточины на самом деле, пока неизвестно. Многие учёные предполагают, что червоточины — лишь проекции четвёртого пространственного измерения, которое мы не можем воспринимать — так, как двумерные существа могли бы воспринимать только отдельные срезы трёхмерных объектов.

В 1995 году Мэтт Виссер предположил, что во Вселенной может существовать множество червоточин, если в ранней Вселенной возникли космические струны с отрицательной массой. Некоторые физики, например, Кип Торн, предложили способы искусственного создания червоточин.

Для упрощённого представления о червоточине представим пространство в виде двумерной поверхности. В этом случае червоточина выглядела бы как отверстие в этой поверхности, ведущее в трёхмерную трубу, выходящую в другом месте двухмерной поверхности. У реальной червоточины будет просто на одно пространственное измерение больше. Например, вместо круглых отверстий на двумерной плоскости мы можем представить себе вход и выход из червоточины в виде сферических отверстий в трёхмерном пространстве, ведущих в четырёхмерную «трубу», похожую на сфериндер.

Червоточины Шварцшильда

Первым обнаруженным (на бумаге) типом червоточины была червоточина Шварцшильда, присутствующая в метрике Шварцшильда, описывающей вечную чёрную дыру. Однако из вычислений получалось, что она разрушается слишком быстро для того, чтобы через неё можно было пройти с одного конца на другой. Считалось, что червоточины, которые можно пройти в обоих направлениях (проходимые), возможны только в том случае, если для их стабилизации будет использована экзотическая материя с отрицательной плотностью энергии. Однако позже физики сообщили, что микроскопические проходимые червоточины возможны и не требуют никакой экзотической материи, вместо этого требуется только электрически заряженная фермионная материя с достаточно малой массой, чтобы она не могла коллапсировать в заряженную чёрную дыру.

Хотя такие червоточины, если они возможны, могут иметь ограниченные возможности – к примеру, передавать только информацию — преодолимые человеком червоточины тоже могут существовать, если наша реальность описывается второй моделью Рэндалла-Сундрума, теорией, использующей браны.

Мосты Эйнштейна-Розена

Червоточины Шварцшильда, также известные как мосты Эйнштейна-Розена — это связь между разными областями пространства, возникающая в вакуумных решениях уравнений поля Эйнштейна. По современным представлениям они неотъемлемая часть максимально расширенной версии метрики Шварцшильда, описывающей вечную чёрную дыру без заряда и вращения. Под «максимальной расширенностью» тут имеется в виду идея о том, что у пространства-времени нет «краёв»: любую возможную траекторию свободно падающей частицы (следующей по геодезической кривой в пространстве-времени) можно продолжить произвольно далеко в будущее или прошлое частицы.

Чтобы удовлетворить это требование, в дополнение к внутренней области чёрной дыры, в которую попадают частицы при падении через горизонт событий, должна существовать отдельная внутренняя область «белой дыры», которая позволяет нам экстраполировать траектории частиц, которые внешний наблюдатель видит поднимающимися вверх от горизонта событий.

Мост Эйнштейна-Розена открыл Людвиг Фламм в 1916 году, через несколько месяцев после того, как Шварцшильд опубликовал своё решение. Затем его вновь открыли Альберт Эйнштейн и его коллега Натан Розен, которые опубликовали свой результат в 1935 году. Однако в 1962 году Джон Арчибальд Уилер и Роберт У. Фуллер опубликовали работу, в которой показали, что этот тип червоточины нестабилен, если он соединяет две части одной и той же вселенной, и что он будет слишком быстро сокращаться для того, чтобы свет (или любая частица, движущаяся медленнее света), приходящий из одной области пространства-времени, мог попасть в другую его область.

Согласно общей теории относительности, гравитационный коллапс достаточно компактной массы образует сингулярную чёрную дыру Шварцшильда. Но в теории гравитации Эйнштейна-Картана-Сиама-Киббла она образует обычный мост Эйнштейна-Розена. В этой теории коллапсирующая материя достигает огромной, но конечной плотности, и не доходит до сингулярности, образуя вместо этого мост.

Хотя червоточины Шварцшильда не проходимы в обоих направлениях, их существование вдохновило Кипа Торна представить себе проходимые червоточины, которые можно создать через открытия «горла» червоточины Шварцшильда экзотической материей с отрицательной массой/энергией.

Проходимые червоточины

Из эффекта Казимира следует, что квантовая теория поля позволяет плотности энергии в определённых областях пространства быть отрицательной по отношению к обычной энергии вакуума материи, и теоретически было показано, что квантовая теория поля допускает состояния, когда энергия может быть произвольно отрицательной в данной точке. Многие физики (в частности, Стивен Хокинг и Кип Торн) утверждали, что такие эффекты могут сделать возможной стабилизацию проходимой червоточины.

Единственный известный естественный процесс, который теоретически предсказывает образование червоточины в контексте общей относительности и квантовой механики, был предложен Леонардом Сасскиндом в его гипотезе ER = EPR. Гипотеза квантовой пены иногда используется для предположения, что крошечные червоточины могут спонтанно появляться и исчезать на планковских масштабах, а стабильные версии таких червоточин были предложены в качестве кандидатов на тёмную материю. Также было высказано предположение, что если бы крошечная червоточина, удерживаемая открытой космической струной с отрицательной массой, появилась во время Большого взрыва, она могла бы раздуться до макроскопических размеров в результате космической инфляции.

Лоренцевы проходимые червоточины позволяли бы очень быстро перемещаться в обоих направлениях из одной части Вселенной в другую часть той же Вселенной или позволяли бы путешествовать из одной Вселенной в другую. Возможность существования проходимых червоточин в общей теории относительности была впервые продемонстрирована в работе Гомера Эллиса в 1973 году и независимо в работе К. А. Бронникова в 1973 году.

Кип Торн и его аспирант Майк Моррис независимо друг от друга обнаружили в 1988 году теоретическую возможность существования червоточин Эллиса и выступили за её использование в качестве инструмента для преподавания общей теории относительности. По этой причине предложенный ими тип проходимой червоточины, удерживаемой открытой сферической оболочкой из экзотической материи, также известен как червоточина Морриса-Торна.

Позже были открыты другие типы проходимых червоточин как допустимые решения уравнений общей теории относительности, включая разновидность, проанализированную в работе Мэтта Виссера 1989 года, в которой путь через червоточину может быть проложен так, чтобы он не проходил через область экзотической материи.

Червоточины для путешествий во времени

Червоточины соединяют две точки в пространстве-времени, что означает, что они в принципе позволяют путешествовать как во времени, так и в пространстве. В 1988 году Моррис, Торн и Юртсевер придумали, как преобразовать червоточину, проходящую через пространство, в червоточину, проходящую через время, путём ускорения одного из двух её входов.

Предлагаемая машина для путешествий во времени, использующая проходимую червоточину, гипотетически может работать следующим образом: один конец червоточины ускоряется до некоторой скорости, сравнимой со скоростью света, (возможно, с помощью продвинутой двигательной системы), а затем возвращается в исходную точку. Альтернативный способ заключается в том, чтобы взять один вход в червоточину и переместить его в гравитационное поле объекта, который имеет более высокую гравитацию, чем другой вход, а затем вернуть его в положение рядом с другим входом. При обоих этих методах замедление времени приводит к тому, что конец червоточины, который был перемещён, стареет меньше, или становится «моложе», чем неподвижный конец, с точки зрения внешнего наблюдателя; однако течение времени внутри червоточины из-за этого не меняется, так что синхронизированные часы на обоих её концах всегда будут оставаться синхронизированными с точки зрения наблюдателя, проходящего через неё.

В результате, наблюдатель, вошедший в «младший» конец червоточины, выйдет из «старшего» конца в тот момент времени, когда возраст старшего конца совпадал с возрастом младшего – то есть, фактически вернётся назад во времени, с точки зрения внешнего наблюдателя. Одно существенное ограничение такой машины времени заключается в том, что вернуться в прошлое можно не ранее момента первоначального создания машины — получается скорее временной путь, чем устройство, движущееся назад во времени. Тем не менее, временные парадоксы, связанные с такими путешествиями, всё равно могут возникнуть.

Возможное решение парадоксов, возникающих в результате путешествий во времени с помощью червоточин, основывается на многомировой интерпретации квантовой механики. Судя по некоторым работам, тела, преодолевающие подобную «временную червоточину», окажутся не в прошлом своей вселенной, а в параллельной вселенной.