Недавно Youtube (*сайт, нарушающий закон РФ) порекомендовал мне любопытный с различных сторон видеоролик. В нём рассматривалась задача, которую, по словам автора, задали его знакомому на собеседовании при приёме на работу в Apple. Эту задачу его знакомый решить не смог.
Сама задача такая. Имеем структуру данных, представляющую собой односвязный список. В каждом узле списка располагается его уникальный номер (не обязательно в порядке связности списка) и указатель на следующий узел. Необходимо определить, есть ли в этом списке цикл (очевидно, что цикл в односвязном списке может быть максимум один) и если есть, то напечатать номер первого узла этого цикла в порядке обхода списка.
Это было проиллюстрировано следующей картинкой:
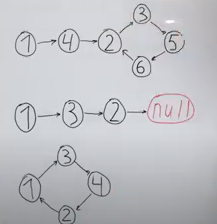
Очевидно, в данных трёх вариантах ответы будут, соответственно, "2", "нет" и "1".
Здесь читателям предлагается придумать свой алгоритм, посмотрев пока на картинку для привлечения внимания.

Следующим шагом зрителям в ролике давалась подсказка: если кто придумал сохранять пройденные узлы в какой-то своей структуре данных и проверять каждый новый узел на присутствие в этой структуре, то такое решение плохое, так как алгоритм не должен требовать O(n) дополнительной памяти.

Настоящим шоком для меня оказалось следующее: больше половины из отметившихся под роликом комментаторов не только не смогло найти решение при указанном ограничении, но и вообще сочло такую задачу имеющей неподъёмную сложность и лишённой практического смысла. По мнению этих людей, данная задача далеко превосходит по своей сложности всё, что когда-либо может понадобиться программисту в жизни.
Это было первое, чем я хотел бы поделиться с читателями. Я просто не могу держать такое знание в себе. Мои представления о типичном уровне людей, профессионально занимающихся программированием, сильно изменились. Конечно, далеко не все смотрят такие ролики, но и не все, наверняка, нашли в себе смелость написать, что они ничего не понимают.
Теперь перейдём к предложенному автором ролика (и, видимо, сообщённому в Apple неудачному претенденту) решению задачи.
Предлагается завести два указателя по схеме "черепаха и кролик", первый из которых продвигается от начала списка со скоростью 1 узел за шаг, а второй – со скоростью 2 узла за шаг. Если список линейный, то второй указатель рано или поздно выйдет на его конец, а если циклический – то указатели рано или поздно встретятся. Далее более тонкими рассуждениями можно показать, что после встречи, если продвигать два указателя по 1 узлу за шаг, начав от начала списка и от места встречи соответственно, то эти указатели встретятся в начале цикла.
Это весьма остроумный алгоритм, однако оправдан ли он? Тут в комментариях развернулись споры между той частью мыслящего меньшинства, которая самостоятельно пришла к такому же алгоритму, и другой частью мыслящего меньшинства, предлагающей метить узлы.
Действительно, более простым решением в предложенной постановке задачи будет такое. Использовать один указатель, и в каждом пройденном узле менять, например, значение номера на отрицательное. Как только мы встретили отрицательное число – это и есть первый узел цикла. Если почему-то мы не хотим жертвовать знаковым битом номера узла, то можем использовать, например, младший или старший биты указателя на следующий узел.
Если нам требуется сохранить список в исходном виде (о чём, заметим, в постановке задачи ничего не сказано), то мы можем сделать дополнительный проход для восстановления наших битиков.
Конечно, возникает некоторое внутреннее сопротивление к модификации списка, переданного в качестве входного параметра. Но заметим, что классики вроде Кнута и Дейкстры зачастую учили программировать именно так, приводя алгоритмы с временным обращением направления связей и тому подобными приёмами.
Сравним эффективность алгоритма кролика-черепахи и алгоритма с маркировкой.
Алгоритм кролика-черепахи не гарантирует нам, что указатели встретятся на первом же обороте цикла, быстрый указатель может сначала перескочить медленный. Поэтому у нас может образоваться лишний проход быстрого указателя по циклу. Поскольку нам надо проводить по списку два указателя, то количество операций доступа к памяти и проверки в среднем навскидку где-то около 2*N + 1.5*L, где N – длина списка, а L – длина цикла. Всё это будут операции чтения.
Алгоритм с маркировкой требует только одного указателя и гарантированно находит начало цикла сразу, поэтому количество операций доступа к памяти и проверки будет N, если мы не восстанавливаем список, и 2*N, если восстанавливаем. Но доступ в данном случае состоит из чтения и записи.
Проверим наши соображения на практике. Запрограммируем алгоритмы на языке Си. В алгоритме кролика и черепахи немножко облегчим себе жизнь и начнём движение указателей сразу со второго шага, чтобы не утяжелять проверку в цикле начальным равенством указателей. Для простоты отрицательный ответ обозначим номером вершины 0.
Алгоритм кролика и черепахи:
#include <stdio.h>
#include <time.h>
int main () {
#define SIZE 100000000
struct Node {
long num;
struct Node *next;
};
static struct Node array [SIZE];
long i, time1, time2, loopnode;
struct Node *ptr1, *ptr2;
for (i=0; i<SIZE-1; i++) {
array [i].num = i+1;
array [i].next = &array[i+1];
}
array [SIZE-1].num = SIZE-1;
array [SIZE-1].next = &array[1];
time1 = clock();
ptr1 = &array[1];
ptr2 = &array[2];
while ((ptr2 != NULL) &&
(ptr2->next != NULL) &&
(ptr1 != ptr2)) {
ptr1 = ptr1->next;
ptr2 = ptr2->next->next;
}
if (ptr1 != ptr2)
loopnode = 0;
else {
ptr1 = &array[0];
while (ptr1 != ptr2) {
ptr1 = ptr1->next;
ptr2 = ptr2->next;
}
loopnode = ptr1->num;
}
time2 = clock();
printf ("Loopnode is %ld, time is %ld\n",
loopnode, time2-time1);
return 0;
}Алгоритм с маркировкой:
#include <stdio.h>
#include <time.h>
int main () {
#define SIZE 100000000
#define RESTORE Y
struct Node {
long num;
struct Node *next;
};
static struct Node array [SIZE];
long i, time1, time2, loopnode;
struct Node *ptr1, *ptr2;
for (i=0; i<SIZE-1; i++) {
array [i].num = i+1;
array [i].next = &array[i+1];
}
array [SIZE-1].num = SIZE-1;
array [SIZE-1].next = &array[1];
time1 = clock();
ptr1 = &array[0];
while ((ptr1->num > 0) && (ptr1->next != NULL)) {
ptr1->num = -ptr1->num;
ptr1 = ptr1->next;
}
if (ptr1->next == NULL)
loopnode = 0;
else
loopnode = -ptr1->num;
#ifdef RESTORE
ptr1 = &array [0];
while ((ptr1 != NULL) && (ptr1->num < 0)) {
ptr1->num = -ptr1->num;
ptr1 = ptr1->next;
}
#endif
time2 = clock();
printf ("Loopnode is %ld, time is %ld\n",
loopnode, time2-time1);
return 0;
}Откомпилируем их при помощи Apple clang 14.0.3 и посчитаем время выполнения на Mac mini с процессором Intel Core i3 3.6 GHz.
оптимизация -O0 |
оптимизация -O3 |
|
Кролик и черепаха |
522082 |
347758 |
Маркировка с восстановлением |
726725 |
340528 |
Маркировка без восстановления |
363929 |
171820 |
Таким образом, более простой алгоритм маркировки с восстановлением не только существенно не уступает кролику и черепахе по производительности, но и в ряде случаев превосходит. А маркировка без восстановления лучше кролика и черепахи вдвое (так как зарплату платить надо одной черепахе).
Какие мысли имеются у читателей по данному поводу?
P.S. Слава богу, есть на свете много умных людей, судя по комментариям. А то я реально испугался, глядя на ютуб.
Комментарии (135)

OldFisher
23.06.2023 10:48+5Алгоритм кролика-черепахи не гарантирует нам, что указатели встретятся на первом же обороте цикла, быстрый указатель может сначала перескочить медленный. Поэтому у нас может образоваться лишний проход по циклу.
Но ведь прыжок "кролика" на 2 шага - не атомарная операция, и ему ничто не помешает проверять совпадение и на промежуточном узле тоже.

vadimr Автор
23.06.2023 10:48Справедливое замечание.
Но в смысле производительности это не особенно влияет.

pda0
23.06.2023 10:48Не на промежуточном. Вместо скорости черепаха - 1, кролик - 2, использовать черепаха - 0.5, кролик - 1. Т.е. каждый цикл сдвигаем указатель кролика, а черепаший только каждую чётную (или не чётную) итерацию. Прос их скорость работы можно попробовать выровнять дополнительным указателем пометки. Помечаем позицию кролика, затем не трогаем её, пока её не догонит черепаха. Если догнала, то помечаем текущее положение кролика. А критерием остановки станет: 1. если достигнут конец незамкнутого списка. 2. кролик на первом элементе списка (кольцо). 3. кролик догнал черепаху. 4. кролик догнал помеченный указатель.
Чисто на пальцах тогда кол-во операций на поиск петли устремиться в 1.5*N в среднем...

vadimr Автор
23.06.2023 10:481 и 2 – это по сути то же самое, что 0.5 и 1.
А если кролик будет двигаться с переменной скоростью, тогда я не представляю, как искать точку входа в цикл. В текущем алгоритме всё построено на том, что кролик – как бы вторая гармоника черепахи, находится с ней в резонансе.

SiGGthror
23.06.2023 10:48На самом деле алгоритм как раз гарантирует встречу на первом проходе черепахи, оптимизация не нужна

vadimr Автор
23.06.2023 10:48Как он может это гарантировать? Всё зависит от чётности длины пути.

SiGGthror
23.06.2023 10:48
vadimr Автор
23.06.2023 10:48Я не знаю, что вы этим хотите сказать, но если вы банально разберёте по шагам третий пример на картинке, то там кролик перепрыгивает черепаху и обегает цикл два раза, прежде чем встретится с черепахой.

SiGGthror
23.06.2023 10:48Я хочу сказать именно то что и написал - гарантируется что за первый проход черепахи по циклу кролик ее встретит. Доказательство - по ссылке. Третий пример вырожденный, потому что там "хвост" = 0, очевидно что он ее перескочит, т.к. мы уже находимся в цикле.

vadimr Автор
23.06.2023 10:48Оптимизация нужна для того, чтобы кролик встретил черепаху за первый свой совместный с черепахой проход по циклу, а не первый проход черепахи. За один проход черепахи кролик успевает обернуться два раза, это в наихудшем случае лишние L*1.5 операций по сравнению с неоптимизированной версией (лишние полкруга проходит черепаха и лишний круг проходит кролик).

SiGGthror
23.06.2023 10:48Оптимизация нужна для того, чтобы кролик встретил черепаху за первый свой проход по циклу, а не первый проход черепахи
Тогда у меня вопрос - как найти начало цикла в вашей оптимизированной версии?

vadimr Автор
23.06.2023 10:48Это не моя оптимизированная версия, но ответ простой – отъехать кроликом на одну клетку назад (т.е. на место встречи, которое он перепрыгнул бы), а черепахой на одну клетку вперёд (т.е. начать во второй раз черепахой со второго узла), чтобы скомпенсировать изменившуюся чётность:
while ((ptr2 != NULL) && (ptr2->next != NULL) && (ptr1 != ptr2) && (ptr1 != ptr2->next)) { ptr1 = ptr1->next; ptr2 = ptr2->next->next; } if (ptr1 == ptr2->next) { ptr2 = ptr1; ptr1 = &array[1]; } else ptr1 = &array[0]; if (ptr1 != ptr2) loopnode = 0; else { while (ptr1 != ptr2) { ptr1 = ptr1->next; ptr2 = ptr2->next; } loopnode = ptr1->num; }
SiGGthror
23.06.2023 10:48Дело - не в четности как таковой. Тот факт что X(n) = X(2n) дает гарантию, что после того как мы скинем один из указателей на начало списка встреча произойдет в начале цикла. Есть ли такая гарантия после оптимизации?

vadimr Автор
23.06.2023 10:48Да, может я и неправ.
Тогда получается, что алгоритм неоптимизируемо содержит дофига лишних операций.

SiGGthror
23.06.2023 10:48Я бы не назвал это "лишними операциями". Задача стоит в поиске такой ноды, в которой черепаха равноудалена от начала, а кролик равноудален от черепахи. После ее нахождения мы точно:
можем сказать, что в списке есть цикл
найти начало цикла
вычислить его длину
При этом гарантируется, что при наличии цикла такая нода встретится при первом проходе черепахи по нему. На мой взгляд это крайне изящный алгоритм)

vadimr Автор
23.06.2023 10:48Алгоритм с маркировкой позволяет всего этого достичь ровно за N*2 обращений к вершинам (если мы восстанавливаем исходную структуру), что в наиболее неудачном случае на 75% быстрее.

sepulkary
23.06.2023 10:48+2Эта задача помечена как "Easy" на Leetcode. Там же, в разделе "Solutions" описаны примерно 8000 решений с использованием широкого спектра языков программирования и алгоритмических подходов.

vadimr Автор
23.06.2023 10:48+1По ссылке приведена более простая задача, где требуется просто обнаружить наличие цикла. Если действовать методом кролика и черепахи, то основная сложность состоит в рассуждении, необходимом для поиска начала цикла.

Akina
23.06.2023 10:48Это сложность выбранного способа решения, а не собственно задачи.
Но она действительно сложнее литкодовской. А более сложная эта задача потому, что поставлено дополнительное условие не использовать дополнительную память для накопления списка пройденных узлов. Без этого условия задача становится чуть ли не тривиальной, и необходимость найти начало цикла её почти не усложняет.

Politura
23.06.2023 10:48В самом низу задачки:
Follow up: Can you solve it using
O(1)(i.e. constant) memory?

datacompboy
23.06.2023 10:48+4А где, кстати, доказательство что движение из точки встречи приведёт именно к началу цикла? Самое важное в посте отсутствует :)

vadimr Автор
23.06.2023 10:48Если вообще они встретятся, двигаясь оба с одинаковой единичной скоростью, то не могут первоначально встретиться ни в каком другом месте, кроме начала цикла, так как это точка объединения их траекторий.

avdx
23.06.2023 10:48+1"Далее более тонкими рассуждениями можно показать, что после встречи, если продвигать два указателя по 1 узлу за шаг, начав от начала списка и от места встречи соответственно, то эти указатели встретятся в начале цикла."
Насколько я могу судить, это неверно. На мой взгляд правильное решение, это делать по одному шагу из начала списка, и после каждого такого шага делать полный круг из точки встречи.

SiGGthror
23.06.2023 10:48+2Это абсолютно точно верно. Вообще об этой задаче проще становится думать (по крайней мере лично мне) когда ты цикл представляешь в виде бесконечной числовой последовательности, часть которой постоянно повторяется. Место их встречи - это некое количество шагов, которое прошла черепаха и по свойствам цикла это количество делится нацело на длину цикла. Если вернуть черепаху в начало то разница в расстояниях между ними - это удвоенное расстояние которое прошла черепаха, но которое все еще делится нацело на длину цикла. А значит, что как только черепаха, двигаясь от начала, попадет на начало цикла кролик будет там же.

datacompboy
23.06.2023 10:48Даже если расстояние до начала цикла взаимопростое с длиной цикла?
Кстати, оптимизация "заец проверяет пересечение когда бежит" ломает гарантию встречи вначале

SiGGthror
23.06.2023 10:48Я ни про какие оптимизации не говорил, я про классический вариант алгоритма. Расстояние до начала цикла особо не имеет значения, оно влияет только на количество шагов до встречи черепахи и кролика в первый раз, свойства алгоритма от этого не меняются

datacompboy
23.06.2023 10:48Я про кратность расстояния - не понимаю как оно гарантирует встречу в начале цикла.
А оптимизация это мысли вслух по поводу

SiGGthror
23.06.2023 10:48У самого цикла есть характеристика - его длина. И есть свойство - если мы выберем любую ноду внутри цикла и пройдем число шагов кратное его длине мы окажемся в том же месте. Т.к. расстояние между черепахой и кроликом как раз такое число, то если мы начнем бежать черепахой сначала списка, то начало цикла как раз и есть первая нода, в которой они встретятся.

qw1
23.06.2023 10:48+3Обозначим
r — "длина ручки", оно же число узлов до входа в цикл.
L — длина цикла.Пусть до первой встречи черепаха прошла r+t шагов, то есть r шагов вне цикла, t — внутри цикла. Черепаха стоит на позиции цикла
r+t-r (mod L) = t (mod L)
(считаем, что начальная нода цикла имеет номер 0).Заяц за это время прошёл 2(r+t) шагов и стоит на позиции цикла
2(r+t)-r (mod L) = r+2t (mod L)Т.к. позиции одинаковые,
t = r+2t (mod L)
r+t = 0 (mod L)То есть, от той позиции t (mod L), где сейчас стоит черепаха, до стартовой позиции цикла 0, нужно сделать r шагов.
Запускаем зайца с начала "хвостика" с единичной скоростью, он делает r шагов по хвостику до входа в цикл. Черепаха делает за это время те же r шагов, и они встречаются в начале цикла.

datacompboy
23.06.2023 10:48Черепаха стоит на позиции цикла
r+t-r (mod L) = t (mod L)
Так вот это утверждение и требует доказательства...

qw1
23.06.2023 10:48Это равенство было лишним (в левой части подсчёт шагов с начала движения, в правой части — с момента входа в цикл).
Достаточно было просто написать:
Пусть t — число шагов, которое черепаха прошла внутри цикла. Тогда она стоит на позиции цикла t (mod L)

SiGGthror
23.06.2023 10:48На сколько я помню, до гарантируется, что первое r + t:
r < r + t < r + L
0 < t < L
Т.е. остаток от деления здесь тоже лишний

vadimr Автор
23.06.2023 10:48+1Он не лишний в том смысле, что задаёт формализм рассмотрения. То есть это арифметика по модулю, а не операция нахождения остатка.
В частном случае операции +mod и =mod могут совпадать с + и =, но нам это неважно.

qw1
23.06.2023 10:48гарантируется, что первое r + t: 0 < t < L
Для меня не очевидно, что заяц не обгонит черепаху на первом круге, а точно в неё попадёт. Если это так, надо доказывать.
Строго говоря, надо доказывать, что позиция когда-нибудь совпадёт. Это так, потому что скорости, 1 и 2, взаимно простые (upd. если точнее, необходимо, чтобы разница скоростей была взаимно простой с L)

datacompboy
23.06.2023 10:48Более того, тривиально привести пример когда не встретятся на первом круге

SiGGthror
23.06.2023 10:48+1Строго говоря, надо доказывать, что позиция когда-нибудь совпадёт. Это так, потому что скорости, 1 и 2, взаимно простые.
Свойство цикла: X(n) = X (n + k * L), где k - натуральное число, а L - длина цикла. Словами: если мы из любой ноды пройдем количество шагов кратное циклу мы окажемся в ней же.
В случае если X(n) = X(2n), то n (mod L) = 0 из свойства выше, т.е. n = k * L.
Теперь можно показать, если n - первое такое число (их больше чем одно), то r < n < r + L
n > r - т.к. такое X(n) = X(2n) справедливо только для нод внутри цикла.Теперь покажем что r + L > n
r = z * L + y, где y = r (mod L) и принадлежит натуральным числам.
Пусть первым n, которое больше r и делится без остатка на L будет r + t, или
z * L + y + t
Т.к. n (mod L) = 0, то y + t = L, или t = L - y
Получается что:
r + L > r + L - yНеравенство выполняется, потому что y - натуральное число
Выходит что r < n < r + L

qw1
23.06.2023 10:48Довольно сложное (как по мне) доказательство, но ошибок я не нашёл.
Ключевой момент тут
X(n) = X(2n) ↔ n = 0 (mod L)
импликация работает в обе стороны.Это значит, подходящее число n повторяется каждые L шагов, и на цикле длины L оно встретится на первом круге.

SiGGthror
23.06.2023 10:48Вы все верно ухватили, у Кнута именно это и было написано, дальше я лишь доказал тот факт, что если мы ищем ближайшее к r число которое делится на L без остатка, то оно будет лежать в промежутке от r до r + L

SiGGthror
23.06.2023 10:48То есть, от той позиции t (mod L), где сейчас стоит черепаха, до стартовой позиции цикла 0, нужно сделать r шагов.
Я бы только уточнил, что до позиции цикла 0 будет
L - t шагов, но при этом есть гарантия, что если мы стоя на позиции t пройдем r шагов - мы попадем в начало цикла.

SiGGthror
23.06.2023 10:48+1Если мне не изменяет память, то позицию черепахи надо бы сбросить на начало списка, тогда их встреча будет в начале

KongEnGe
23.06.2023 10:48+11Если кандидат предложит вам решение на базе модификации указателй -- гоните его в шею, это человек без внутренних тормозов, который и в прод такую чернуху протянет потом :)

vadimr Автор
23.06.2023 10:48+2Есть сермяжная правда в ваших словах, но в системном программировании такое встречается :)
В частности, в сборщиках мусора любимое дело размещать свои временные данные в собираемом мусоре.

kinh
23.06.2023 10:48Я часто использую модификацию указателей. Если адрес выровнен на границе 4 байт, то это значит, что младшие 2 бита указателя всегда 0, и их можно использовать в качестве битовых флагов. В задаче из статьи один из битов можно использовать для пометки того, что элемент уже пройден. Если нам попадётся элемент с этим установленным битом, то в списке - цикл.
// Распределение блока памяти, всегда выровненного на границе 4 байт unsigned char *real_block = (unsigned char *)malloc(num_bytes); // контейнер для блока unsigned char *aligned_block; // выровненный блок if((((size_t)real_block) & 3) == 0) { aligned_block = real_block; } else { // здесь можно использовать _expand(...), но я не стал усложнять пример free(real_block); real_block = (unsigned char *)malloc(num_bytes + 3); size_t correction = (-(int)(size_t)real_block) & 3; aligned_block = real_block + correction; }В качестве блока можно рассматривать массив элементов, используемый для контейнера hive/colony. Из этого контейнера распределяются элементы для списка, и каждый из них будет выровнен на 4 байта.
А для навигации по списку используются методы, а не прямой доступ к полям:
struct ListItem { size_t next_with_flags; int data; ListItem* next() {return (ListItem *)(next_with_flags & (size_t)(ptrdiff_t)~3);} unsigned flags() {return (unsigned)next_with_flags & 3;} };
bay73
23.06.2023 10:48+2Ага, а параллельно этот список читает ещё сотня потоков, которые будут очень рады его модификации.

ZyXI
23.06.2023 10:48Достаточно одного потока и связного списка определённого в виде
struct linked_list; int linked_list_node_number(const struct linked_list *); const struct linked_list *linked_list_next(const struct linked_list *); extern const struct linked_list *start;Попробуйте помодифицировать что‐то, не получив Undefined Behaviour. Для разумных программистов можно даже удалить все
const— одной инкапсуляции достаточно.

Akina
23.06.2023 10:48Алгоритм кролика-черепахи не гарантирует нам, что указатели встретятся на первом же обороте цикла, быстрый указатель может сначала перескочить медленный
Текущий алгоритм с кроликом и черепахой, как я понимаю, двигает и кролика, и черепаху, а затем сравнивает местоположения.
Если же после каждого прыжка хоть кого-то сравнивать местоположения, то никакого "перепрыгнет" не будет. И соответственно не будет потенциального "второго оборота".
В этих условиях при проверке на каждом прыжке можно кролику прыгать не на 2, а на 3 узла. Всё равно мимо не проскочит.

datacompboy
23.06.2023 10:48+2Но при этом возможна лишняя бегодня кролика по циклу, к которому ползёт черепаха

Alexandroppolus
23.06.2023 10:48В этих условиях при проверке на каждом прыжке можно кролику прыгать не на 2, а на 3 узла. Всё равно мимо не проскочит.
Если кролик и черепаха стартуют от двух соседних элементов, как в статье, то попадают на бесконечный цикл, при условии, что длина цикла в списке равна равна 6*n

vadimr Автор
23.06.2023 10:48В статье просто начинаем цикл со второго шага. На первом оба были в нуле.

Alexandroppolus
23.06.2023 10:48Алгоритм кролика и черепахи:
...
ptr1 = &array[1];
ptr2 = &array[2];Я вот об этом.

vadimr Автор
23.06.2023 10:48Именно. Это их позиции на втором шаге. Кролик продвинулся с 0 на 2, а черепаха - с 0 на 1.

Alexandroppolus
23.06.2023 10:48Если что, в этой ветке комментов обсуждается идея двигать зайца не на 2, а на 3 шага.

mpa4b
23.06.2023 10:48+1В приведённых примерах оказывается, что элемены списка лежат подряд, и хождение по нему оказывается равносильно линейному чтению памяти. Для более релевантных результатов хорошо бы для начала "перемешать" список: так, чтобы прыжки по .next были бы в рандомные позиции. И время создания/перемешивания тоже не измерять, а только целевую задачу.

vadimr Автор
23.06.2023 10:48+1Что касается расположения элементов списка, я думал об этом, но в любом случае это вряд ли сильно изменит сравнительную картину – просто возрастут оба времени. Кроме того, вообще не очень очевидно, что рандомные позиции релевантнее последовательных.
Меня в измерениях беспокоил, в основном, ответ на вопрос, не просядет ли производительность из-за операций записи. И на другом процессоре, образца 12-летней давности, она действительно заметно просаживается.
А что касается времени создания, то оно не учитывается.

mpa4b
23.06.2023 10:48+1Интересное наблюдение: первый алгоритм делает 4 прохода по массиву от начала до конца: сначала 3 прохода до совпадения указателей, потом ещё один для нахождения 1ого элемента (один потому что ввиду построенного списка, где конец указывает на 2ой элемент, ptr1 и ptr2 оказываются недалеко друг от друга, и зафетченное в кеш для "спешащего" указателя пригождается чуть позже "опаздывающему"). Второй алгоритм (с восстановлением) тоже делает 4 прохода: один раз вычитывает всю память, тут же (с лагом в размер кеша, предполагая что тот writeback) отписывает обратно, потом ещё раз делает то же самое (для восстановления). Последний алгоритм делает лишь 2 прохода.
По скорости выполнения ровно то и выходит -- 1ый и 2ой время примерно одинаковое, у 3его в 2 раза быстрее.

guryanov
23.06.2023 10:48+2Тут смысл задачи в том, что в элементах списка нельзя ничего хранить.

mpa4b
23.06.2023 10:48+4И тогда получается типичная задача на собеседовании: если не знать подхода, не решишь, если знаешь трюк про шаг по 1 и по 2 -- решишь. По подходу ничем особо не отличается от "почему люки круглые" :)

vadimr Автор
23.06.2023 10:48В таком условии нет особого содержательного смысла. Почему нельзя?
Почему может не хватать лишней памяти – это объяснимо. А тут было бы искусственное ограничение, на мой взгляд.

unreal_undead2
23.06.2023 10:48Почему нельзя?
Например у нас 32битное приложение на 64битной системе (соответственно, практически всё адресное пространство может быть использовано, лишнего бита в адресе нет), а номер элемента - unsigned short (и допустимы списки до 65535 элементов), то есть там тоже битика не найдётся.

vadimr Автор
23.06.2023 10:48+1Даже при таких замороченных условиях будет лишний младший бит адреса, так как 6- или 8- байтовые структуры на практике будут выравнены на 2.

unreal_undead2
23.06.2023 10:48Ok, предположим что у нас используется кастомный аллокатор, который может и нечётные адреса выдавать (на интеловской архитектуре выравнивание не требуется).
Причём всё это может вылезти не сразу, а после того, как код с модификацией протестировали в "обычных" условиях, закоммитили в продукт, странное поведение началось через пару лет, когда автор давно уволился.

vadimr Автор
23.06.2023 10:48Уже многовато героических задач нужно решить простому солдату израильской армии :) По сути, четырёхслойная 8-16-32-64 архитектура.

code_panik
23.06.2023 10:48
code_panik
23.06.2023 10:48+2Можно рассуждать так. Пусть цикл есть. Пусть r - длина ручки списка (число шагов до первого узла в цикле), m - длина цикла. Тогда черепаха делает r + k шагов, где k шагов в цикле. Заяц делает r + t * m + k = 2 * (r + k), где t - полное число проходов по циклу, и т.к. на каждый шаг черепахи 2 шага зайца. Поэтому r + k = t * m, r = t * m - k. Пусть оба встречаются в некотором узле А цикла, тогда после встречи пусть одна черепаха бежит из начала списка, друга из узла А. Тогда они встретятся в искомом узле (начале цикла), потому что пока одна пробегает длину ручки, другая пробегает остаток цикла m - k и делает несколько полных оборотов - число кратное m, если t > 0 это t - 1.

squaremirrow
23.06.2023 10:48+1Как насчет такого ненормального подхода?
Т.к. значение каждого узла ограничено -10^5 <= Node.val <= 10^5, значит можно каждому такому числу сопоставить некое простое число, не превышающее какой-то фиксированный размер в памяти, например взять простое число под номером 2*abs(Node.val) + (sign(Node.val) + 1)//2. При проходе по листу, считаем бегущее произведение прошлых простых чисел, и если простое число, соответствующее текущему Node.val делит это произведение без остатка, значит мы оказались в узле, в котором мы уже раньше были.

code_panik
23.06.2023 10:48Если правильно понял, для этого нужно взаимно-однозначное соответствие между узлами и простыми числами. По ссылке длина списка до 10^4, то есть в случае отсутствия цикла у нас в итоге будет произведение 10^4 первых простых чисел. Множество чисел изначально слишком большое и произведение будет слишком большое. Десятитысячное простое число больше 100000.

rukhi7
23.06.2023 10:48+2Задача действительно лишена практического смысла так как следить за отсутствием циклов в списке надо на этапе создания списка. Если есть вероятность появления такого списка в какой-то реальной программе программу надо переписывать, она не то что не будет работать, она вполне может предстовлять опасность.
Получается это задача о том как правильно подставить костыль. А надо писать так чтобы костыли были не нужны.

vadimr Автор
23.06.2023 10:48Мы ж не знаем прикладного назначения этой структуры данных. Может, она как раз и предназначена для каких-то циклических вещей.

khajiit
23.06.2023 10:48+4В этом случае в структуре должно быть записано где и как она хитровыделана, потому что это напрямую влияет на ее обработку.
UPD: задача, на самом деле, не то что нереалистичная, просто она из серии как сделать через жопу а потом рвать на жопе волосся, героически превозмогая.

rukhi7
23.06.2023 10:48Мы ж не знаем прикладного назначения этой структуры данных
и из этого также следует бесполезность решения любых задач на основе такой структуры данных. Раз мы не знаем прикладного назначения мы ни как не достигнем этого прикладного назначения.

vadimr Автор
23.06.2023 10:48Допустим, вам скажут, что это номера авторитетных инстанций, без согласования которых по правилам нельзя подписать какой-то документ. И мы хотим на всякий случай проверить, что реально существующая в физическом мире цепочка согласований не циклична.

khajiit
23.06.2023 10:48+3А для такой задачи вот это допусловие
Следующим шагом зрителям в ролике давалась подсказка: если кто придумал сохранять пройденные узлы в какой-то своей структуре данных и проверять каждый новый узел на присутствие в этой структуре, то такое решение плохое, так как алгоритм не должен требовать O(n) дополнительной памяти.
не имеет смысла. Если это единичная проверка входных данных, которая отрабатывает раз в год, то она должна в первую очередь проверять данные, во вторую — быть понимаемой, читаемой и редактируемой, а заниматься хитрыми извращениями — в самую распоследнюю.

rukhi7
23.06.2023 10:48+1и при чем тогда здесь указатели, и связанный список?
Потом вы допустили одно, он другое, кто то третье, решать будем что-то в среднем что ли? Вы считаете это имеет смысл?

code_panik
23.06.2023 10:48+1Задача действительно лишена практического смысла
Нет. Пусть есть последовательность зависимостей, которую нужно проверить на отсутствие циклов. Циклы могут образовывать зависимости, например, в программных файлах, включаемых друг в друга, или в вызывающих друг друга функциях. Тут https://youtu.be/Qc8zuhaqWPM?t=457 Тим Кейн рассказывает о таком случае в разработке Arcanum. Он решает её добавлением ограничения на количество вложенных вызовов. Эта задача - разновидность задачи поиска цикла в графе. Она возникает в самых разных местах. Именно о задаче из статьи впервые услышал на лекции Степанова А.А. в Яндексе. Яндекс, кажется, местами отмирает - не могу найти ссылку на лекцию, а та что есть не работает.

rukhi7
23.06.2023 10:48Пусть есть последовательность зависимостей
Если можно начать с "Пусть", я предпочту начать так:
(А-) Пусть ее НЕТ, этой последовательности зависимостей ...
В том смысле, например, что давайте не будем ее допускать по мере формирования списка, список то в памяти все равно как то формируется, а не из сферической реальности прилетает!
Гоголь когда-то написал:
Тогдашний род учения страшно расходился с образом жизни: эти схоластические, грамматические, реторические и логические тонкости решительно не прикасались ко времени, никогда не применялись и не повторялись в жизни. Учившиеся им ни к чему не могли привязать своих познаний, хотя бы даже менее схоластических. Самые тогдашние ученые более других были невежды, потому что вовсе были удалены от опыта.

qw1
23.06.2023 10:48реторические
Эх, Гоголь, Гоголь...

vadimr Автор
23.06.2023 10:48+2Тут смешно. По старой орфографии действительно было “реторическiя” и затем “реторические”. Процитировано, видимо, по изданию 1933 года.

rukhi7
23.06.2023 10:48Здорово! Там где рассуждают о том кто быстрее черепаха или кролик или когда они встретятся бегая в лабиринте, не грех и орфографию Гоголя обсудить!
Я то, понятно, орфографию не проверял, скопировал откуда-то изначально, пол года назад, сыну показать. Не как не думал что возможны такие нюансы :) .

andybiiig
23.06.2023 10:48+1Если модификация списка не запрещена, есть один вариант, только я его до конца не додумал. Таки да, на первом проходе надо указатели разворачивать, тогда или (1) список закончится (циклов нет), или (2) мы вернёмся к его началу. При этом надо считать количество шагов L. При исходе (1) можно список развернуть обратно. При исходе (2) у нас будет элемент в позиции L/2, который является самой дальней точкой и находится точно в середине цикла (или два элемента, с учётом четности L). Нам нужно дойти до него (опять же, разворачивая указатели) и дальше идти по обеим веткам обратно, пока указатели не укажут на один элемент, это и будет начало цикла. При этом ветку, которая идёт "вперёд", надо разворачивать, а ветку, которая идёт "назад" и по которой мы пришли в L/2, разворачивать не надо. Тогда после завершения поиска у нас список вернется в исходное состояние.
Возможно, я сейчас изобрёл велосипед, который описан где-то в умных книгах. Зато сам)

shasoftX
23.06.2023 10:48+2В каждом узле списка располагается его уникальный номер (не обязательно в порядке связности списка)
А обязательно ли нумерация начинается с 1 и нет пропусков в нумерации? А то ведь можно просто считать максимум и количество пройденных узлов. Как только превышение, значит мы на первом узле кольца. Само собой если встретили null, то кольца нет


rukhi7
23.06.2023 10:48+1осталось только выяснить откуда взять количество узлов в списке, когда список зациклен их посчитать не получится.
Как я уже писал выше:
Задача действительно лишена практического смысла так как следить за отсутствием циклов в списке надо на этапе создания списка. Если есть вероятность появления такого списка в какой-то реальной программе программу надо переписывать, она не то что не будет работать, она вполне может предстовлять опасность.

shasoftX
23.06.2023 10:48откуда взять количество узлов в списке
Так посчитать можно.
int count = 0; int maxId = 0; Node *item = <первый элемент>; while(item!=null) { maxId = max(maxId, item->info); count++; if(count > maxId) { printf("Первый элемент цикла %i",item->info); break; } item = item->link; } if(head==null) { printf("Нет циклов"); }Если начинается всегда с 1-го номера и без пропусков, то даже если они не по порядку, то алгоритм будет работать.

rukhi7
23.06.2023 10:48Проблема в том что постоянно вылезают какие-то "если"!
если у item есть item->info
если определена операция max() для (maxId, item->info)
Это только то что вы придумали, выше смотрите другие варианты!
При таком количестви "если" это превращается в какой-то маразматический перебор для всех "если" и "не-если".
Лично я вот, очень не люблю маразматические переборы, и к тем кто их устраиваевает отношусь с недоверием, мягко говоря.

vadimr Автор
23.06.2023 10:48+1Я считаю, что задача для интервью должна решаться в том виде, в каком она была поставлена. Если человек нарисовал в качестве примеров три схемы с последовательными натуральными числами и ничего больше не сказал, то имеет право получить решение в соответствии со своим ТЗ. Поэтому, с моей точки зрения, важен приведённый скриншот.

shasoftX
23.06.2023 10:48+2если у item есть item->info
если определена операция max() для (maxId, item->info)
Вот это не предположение, а 100% верно исходя из условия задачи. Тут я ничего не придумываю.
"Если" тут только относится к нумерации с 1 и предположения что нумерация идет без пропусков. Про это в условии задачи ничего нет и требуется уточнение. Не "маразматический перебор", а уточнение у постановщика. Вполне допускаю что суть задачи не только в решении, а ещё и в правильно заданном вопросе.

squaremirrow
23.06.2023 10:48+3upd: слишком долго писал комментарий, shasoftX меня опередил
Если мы знаем, что все уникальные номера узлов находятся в пределах от 1 до N, где N — число элементов списка, то есть решение, которое требует одного "прогона" и не меняет исходный список.
Заводим два числа:
- Счетчик количества узлов с начала
- Бегущий максимум встреченных значений элементов
Как только 1-е число оказывается строго больше 2-го, значит мы находимся на искомом элементе входа в "цикл" (если мы конечно не придем в null до этого).
Почему это работает? Потому что максимум инвариантен к перестановкам в списке, и при проходе всех элементов списка мы обязательно получим 2-е число равное N. Поэтому, как только мы вернемся в элемент, который уже посещали до этого, т.е. перейдем в N+1 элемент по счету, мы получим выполнение условия на выход из цикла.

pda0
23.06.2023 10:48+1Если нам во время проверки не требуется читать список из другого потока и временно можно его модифицировать, то возможен другой неожиданный способ - инвертировать список.
Т.е. проходимся по списку, меняем направление ссылки с потомка на родителя. В списке без петель новой головой списка станет хвост. В списке с петлёй мы придём к голове.
Т.е. 1. Инвертируем список. 2. Проверяем равна ли новая голова старой. 3. Восстанавливаем список, снова инвертируя его, относительно новой головы.
Набросал быстро программку для проверки идеи. Вроде работает. Проверить можно здесь.
Что было под рукой...
{$MODE OBJFPC}{$H+} {$R+} type PListNode = ^TListNode; TListNode = record Next: PListNode; Id: Integer; end; function AddNode(PrevNode: PListNode; Id: Integer): PListNode; begin New(Result); Result^.Next := nil; Result^.Id := Id; if PrevNode <> nil then PrevNode^.Next := Result; end; procedure DeleteList(FirstNode, LastNode: PListNode); var DelNode: PListNode; begin repeat DelNode := FirstNode; FirstNode := FirstNode^.Next; if FirstNode = LastNode then FirstNode^.Next := nil; Write(DelNode^.Id, ' '); Dispose(DelNode); until FirstNode = nil; Writeln; end; function InvertList(FirstNode: PListNode): PListNode; var PrevNode, CurrNode, NextNode: PListNode; FirstPass: Integer; begin PrevNode := nil; CurrNode := FirstNode; NextNode := CurrNode^.Next; FirstPass := 0; repeat if CurrNode = FirstNode then FirstPass := FirstPass + 1; CurrNode^.Next := PrevNode; PrevNode := CurrNode; CurrNode := NextNode; if CurrNode <> nil then NextNode := CurrNode^.Next; until (CurrNode = nil) or ((FirstPass = 2) and (PrevNode = FirstNode)); if CurrNode = nil then Result := PrevNode else Result := CurrNode; end; function CheckLoop(FirstNode: PListNode): Boolean; var NewFirstNode: PListNode; begin if FirstNode^.Next <> nil then begin if FirstNode^.Next <> FirstNode then begin NewFirstNode := InvertList(FirstNode); Result := NewFirstNode = FirstNode; InvertList(NewFirstNode); end else Result := True; end else Result := False; end; procedure WriteBool(Value: Boolean); begin if Value then Writeln('True') else Writeln('False'); end; var N1_1, N1_2, N1_3, N1_4, N1_5, N1_6, N2_1, N2_3, N2_2, N3_1, N3_2, N3_3, N3_4: PListNode; begin N1_1 := AddNode(nil, 1); N1_4 := AddNode(N1_1, 4); N1_2 := AddNode(N1_4, 2); N1_3 := AddNode(N1_2, 3); N1_5 := AddNode(N1_3, 5); N1_6 := AddNode(N1_5, 6); N1_6^.Next := N1_2; N2_1 := AddNode(nil, 1); N2_3 := AddNode(N2_1, 3); N2_2 := AddNode(N2_3, 2); N3_1 := AddNode(nil, 1); N3_3 := AddNode(N3_1, 3); N3_4 := AddNode(N3_3, 4); N3_2 := AddNode(N3_4, 2); N3_2^.Next := N3_1; WriteBool(CheckLoop(N1_1)); WriteBool(CheckLoop(N2_1)); WriteBool(CheckLoop(N3_1)); DeleteList(N1_1, N1_6); DeleteList(N2_1, N2_2); DeleteList(N3_1, N3_2); end.

VBKesha
23.06.2023 10:48+4Я не смотрел оригинальное видео и не знаю как там преподносится, но я просто обожаю такие варианты постановки задачи, а именно:
- Вот задача и у вас развязаны руки
- А нет не развязаны, а немного связаны(так как алгоритм не должен требовать O(n) дополнительной памяти), почему сразу это не озвучить
- Подсказка никак не выплывающая из постановки задачи(Использовать один указатель, и в каждом пройденном узле менять, например, значение номера на отрицательное) Оказывается можем колбасить список как ходим.
Да какогож хрена я должен догадаться до пункта два и пункта три.
С такими подходами может от меня ждут что я вообще при помощи файловой системы это решить должен?
pda0
23.06.2023 10:48Да какогож хрена я должен догадаться до пункта два и пункта три.
Ни с какого. Так в общем случае делать нельзя. Такой подход называется "тегирование", но его применение допустимо, лишь если у вас есть дополнительные гарантии. В данном случае, что все числа не отрицательные.
А то так-то и верхний бит указателей на следующий узел можно использовать для пометки.

Zara6502
23.06.2023 10:48Есть универсальное решение, а есть контекстно-зависимое, с оптимизацией под конкретные данные. Так как в задаче про конкретные данные ничего не сказано, то и решение должно быть универсальное. Так как я могу на том же собеседовании сказать, что это поиск петли в readonly БД на 45 петабайт и вся эта маркировка канет в лету.

vadimr Автор
23.06.2023 10:48Если это поиск во внешней памяти, то мы не только вправе, но и обязаны строить кеш в оперативке. Не бывает универсальных решений.

Zara6502
23.06.2023 10:48Если это поиск во внешней памяти, то мы не только вправе, но и обязаны строить кеш в оперативке
нет оперативки
Не бывает универсальных решений
все библиотеки всех языков программирования разом заорали - ведь они, оказывается, не существуют. По-вашему этого просто не существует?

vadimr Автор
23.06.2023 10:48Это существует, но это далеко не универсальный метод. Попробуйте так отсортировать магнитную ленту.

Zara6502
23.06.2023 10:48Это проблема не метода и не реализации, это вопрос организации доступа к оборудованию. Например я пользовался стиммерами HP еще в 2008 году, там всё делала сама железка и софтовая часть в ядре, для Oracle *nix работа ничем не отличалась от работы с SAS СХД или HDD. Соответственно и Sort будет работать, а вопрос эффективности - уже находится в категории "контекстно-зависимое решение".

vadimr Автор
23.06.2023 10:48В принципе будет работать, а практически результата вы не дождётесь.

Zara6502
23.06.2023 10:48прочтите один раз что я написал изначально, потому что вы своими выводами и пришли к моим словам. если вам органически не нравится слово - универсальный, то читайте его как - базовый, будет то же яйцо только вид сбоку.

agalakhov
23.06.2023 10:48+2Метод маркировки (сменой знака) требует O(n) дополнительной памяти. Он возможен в тех случаях, когда в списке изначально присутствуют пустые места, например, пустой знаковый бит. В остальных случаях он нерабочий.

vadimr Автор
23.06.2023 10:48Это игра словами. В любом случае, приводившийся выше в комментариях метод маркировки сменой направления указателя не требует дополнительной памяти даже в вашем определении. При этом он использует меньше проходов по узлам даже в том случае, когда мы восстанавливаем исходное состояние.

qw1
23.06.2023 10:48+1Это игра словами
Это у вас игра словами. Если забывать "мелочи" на расходы памяти, можно написать идеальный архиватор, который любой файл гарантированно уменьшает на 1 байт, перенося этот байт в имя файла. Трюк с записью неиспользуемых бит в указателе примерно такого же рода читерство.
В любом случае, приводившийся выше в комментариях метод маркировки сменой направления указателя не требует дополнительной памяти
Формально, это не метод маркировки, это другой алгоритм. И он по нескольким причинам хуже "зайца и черепахи", потому что
1) требует 2 раза пройти и хвостик, и петлю, восстанавливая указатели как было
2) не находит позицию входа в петлю.
(не говоря уже о модификации данных)
vadimr Автор
23.06.2023 10:48Если забывать "мелочи" на расходы памяти, можно написать идеальный архиватор, который любой файл гарантированно уменьшает на 1 байт, перенося этот байт в имя файла.
Это вполне нормальный ход, если стоит именно такая задача.
Алгоритм с битовой маркировкой имеет заданный вход, заданный выход, заданный расход рабочей памяти и заданный результат работы. Какие вопросы?
Если нам дали на вход структуру данных, содержащую пустые места, это наша законная добыча.
Формально, это не метод маркировки, это другой алгоритм. И он по нескольким причинам хуже "зайца и черепахи", потому что 1) требует 2 раза пройти и хвостик, и петлю,
Алгоритм кролика и черепахи требует от 2 до 3.75 раз пройти все узлы. Указателя-то два.
2) не находит позицию входа в петлю.(не говоря уже о модификации данных)
В этом комментарии намечено, как в таком случае найти точку входа. Хотя это опять-таки лишняя работа.

Andrey_Solomatin
23.06.2023 10:48+1Как вы решали бы эту задачу?
Тестовая задача обычно рассматривается в контексте интервью. В опросе нет ни одного правильного варианта.
Кроме решения задачи, на интервью, смотрят на то, как вы работаете с требованиями и рассуждаете.
Если вы после получения задачи замолчите и вернётесь с идеальным техническим решением, то вы провалили интервью. Пожалуйста, не далайте этой ошибки.
На своём опыте, я бы порекомендовал такую стратегию:
- Проговорить несколько вариантов, хэш, зайц и черепах, маркировка. Объяснить плюсы и минусы (сложность по памяти, сложность выполнения, сложность реализации). В процессе этого уточнять требования, типа: "Подойдёт ли решение O(n) по памяти?" (если вы на сеньёра, то скорее всего нет) или "Влезут ли данне в хэшмэпу?" (она большая, но не бесконечная). "Можно ли мутировать?" (без этого вопроса, предлагать вариант с мутацией, это путь к провалу).
И после этого договориться с интервьюером, какой вариант вы будете решать. По возможности стоит попробовать подтолкнуть интервьюера, к решению, которое вам кажется более простым в реализации.
Этим вы покажете ширину своих знаний и инженерный подход к решению задач. И пойметё, что решаете ту задачу которую нужно. Я как-то похоже на собеседовании сделал, https://habr.com/ru/articles/743514/#comment_25682476, не перезвонили.

igorekudashev
23.06.2023 10:48+1вызвать метод для получения количества элементов в структуре и цикле пройти n + 1 элементов

vadimr Автор
23.06.2023 10:48Если б был метод для получения количества элементов, не было б задачи.

datacompboy
23.06.2023 10:48Это литкод изи... Плюс, не надо недооценивать как много людей могут провалить даже такую реализацию

Andrey_Solomatin
23.06.2023 10:48Нет, изи это просто проверить, что цикл есть, эта задача средняя.
https://leetcode.com/problems/linked-list-cycle-ii/



just-a-dev
А если там unsigned int?
vadimr Автор
Очевидно, надо уточнять условия задачи при её постановке. Но в целом место для лишнего битика мы обычно можем найти, если не в номере ноды, то в указателе.
В любом случае адресуемая память не может вместить столько узлов нашей структуры, сколько возможно адресов. Поэтому место всегда есть.
Правда, баловство с указателями трудноисполнимо в системах программирования со сборщиком мусора.
unreal_undead2
Это если мы чётко знаем, что какие то биты виртуального адреса не используются. А то может оказаться, что памяти выделено меньше, но мапится на разбросанные диапазоны с разными битовыми сочетаниями.
Но я бы скорее о многопотоковости задумался, мало ли кто кроме нас по этому списку ходит...
RomeoGolf
Вопрос даже не в том, есть ли место. Вопрос — не занято ли место? Если номер узла уникальный и не обязательно в порядке узлов, то неизвестно, не встретится ли отрицательный номер в нормальной немаркированной нумерации. Это ведь тоже в условии не запрещено. Возможны ложные срабатывания.
RomeoGolf
И вообще, насчет маркировки с изменением имеющихся данных. В синтетических задачах на голые алгоритмы этот финт ушами выглядит изящно и показывает нестандартность мышления. В реальности имеющиеся в нодах данные могут использоваться кем-то еще в параллельном потоке или по прерываниям, а мы тут их портим внезапно...
unreal_undead2
В реальности я бы запользовал хеш таблицу, а дальше смотрел, насколько проблемно выделение дополнительной памяти на реальных данных.
vadimr Автор
Допустим, хеш совпал. Что это нам даёт?
Это ведь может быть и случайное совпадение.
unreal_undead2
Под хешом имелся в виду std::unordered_map, оно коллизии само обработает.
LedIndicator
Не знаю как у вас в сишечке, а у нас в жаве, если хэш коды совпадают, ноды в HashMap (в нашем случае в HashSet, но неважно) попадают в один бакет, и там хранятся в виде списка или дерева. При доставании ноды с одним хэш кодом сравниваются методом equals. Есть реализация хэш структур со сдвигом, open addressing, так называемый. Там в случае коллизии просто ищется свободный слот.
В реальной жизни в Java я бы тоже применил хэшсет. Не говоря уж о том, что менять на лету айди (а этот инт в узле это именно айди) на отрицательный и обратно так себе идея и, обычно, просто невозможно.
Устройство HashMap это, кстати, любимый вопрос на собеседованиях по Java. Просто всегда задают. Ну, по крайней мере, раньше спрашивали.
vadimr Автор
Чтобы сравнивать сами значения в случае равенства хеш кодов, нужно хранить эти значения, а это запрещено условиями задачи.