Будет 5 статей по темам:

• Последовательные контейнеры

• Ассоциативные контейнеры(Вы тут)

• Стеки и очереди - они же адаптеры

• Функциональные объекты

• Основные алгоритмы - последние будут иногда проскакивать во всех статьях выше

Наполнение статьи про ассоциативные контейнеры:

1) Множества 

• std::set

• std::unordered_set

• std::multiset

2) Словари(ХЭШ-МАПЫ)

• std::map

• std::unordered_map

• std::multimap

Предисловие:

Начиная разбираться в ассоциативных контейнерах нужно обговорить, что вообще такое ассоциативность - если вы в детстве играли в "Ассоциации", то для вас все почти очевидно, ведь для каждого объекта обговариваемого в периоде игры - нужно найти что-то связанное с этим объектом.

Компилятор с вами играть ни во что не собирается и хранит пары ключ-значения, но есть небольшая разница между std::set и std::map.

В std::set мы храним уникальные значения и поэтому эти значения, то есть ваши объекты - числа, строки, буквы, объекты собственных типов - внутри std::set являются как ключами, так и значениями. И std::set гарантирует нам, что все значения уникальны, то ничто не помешает вам сделать ваш УНИКАЛЬНЫЙ объект - КЛЮЧОМ и ЗНАЧЕНИЕМ.

В std::map не предоставляет гарантии о том, что все значения уникальны и как раз там все ваши объекты занумеровываются под некие индексы обычно от нуля до n. Благодаря этому вы получаете быстрый доступ к элементам O(log n).

std::unordered_map, std::map, std::unordered_set - одни из самых часто встречающихся при решении задач на LeetCode. Их использование сильно упрощает вам жизнь и не приходится каждый раз ковыряться в std::vector и дописывать какие-то функции удаления одинаковых элементов, которые все равно работают медленнее, чем ассоциативные контейнеры.

Пропустите этот пассаж до {1) Начиная диалог о множествах} и не обращайте на него внимания, если вам просто нужен конспект для решения задач - это вообще никак не поможет вам в решении задач.

Если вы уже продвинулись в C++, то в курсе про существование std::multiset, где могут храниться одинаковые элементы, хотя в std::set такого быть не может, но как тогда на основе этого можно построить красно-черное дерево.

Конечно нельзя добавлять одинаковые элементы в красно-черное дерево, но внутри std::multiset для одинаковых элементов заводится вектор, куда ваши одинаковые элементы складываются. То есть когда вы вызовете функцию count(), то он найдет ваше значение в красно-черном дереве и если ваш_вектор_с_копиями больше 1 - вы получите длину этого вектора. Все круто, логично и не нарушает красно-черное дерево!

Оговорка: если вы не знаете, что такое красно-черное дерево, то представляйте его как бинарное дерево поиска, если не знаете, что такое двоичное дерево поиска, то представляйте его так:

• забудьте про цвета;

• забудьте про вставку и удаление, там для балансировки нужны будут повороты;

• вы можете взять и четное количество элементов, но тогда у вас появятся не до конца заполненные ветки (в красно-черном дереве они бы отмечались как NIL).

И так, у вас есть упорядоченный набор чисел [от 1 ... до 7] включительно.

Как бы мы укомплектовали это в дерево максимально эффективно?

1) Набор чисел отсортирован по возрастанию и все что нам нужно - это взять элемент по середине {1,2,3,4,5,6,7} - нашли его это 4. Поэтому ставим его на самый верх.

2) После этого мы сохраняем числа левее 4 в вектор {1,2,3} и правее числа 4 в вектор {5, 6, 7}.

3) Оба получившихся вектора сортируем по возрастанию или убыванию.

4) В каждом из этих векторов по отдельности находим число со средним индексом - 2 и 6.

5) Число меньшее нашего верхнего узла 4, а именно 2 помещаем в левый узел, а 6 в правый.

6) Составляем два вектора {1,3} и {4,6} - средний индекс получить не получится, поэтому относительно 2 распределяем 1 и 3, и относительно 6 распределяем 5 и 7.

Поздравляю, вы получили первое бинарное дерево и можете попытаться закодировать его в виде двумерного массива векторов, попробуйте сделать его с четным количеством элементов:

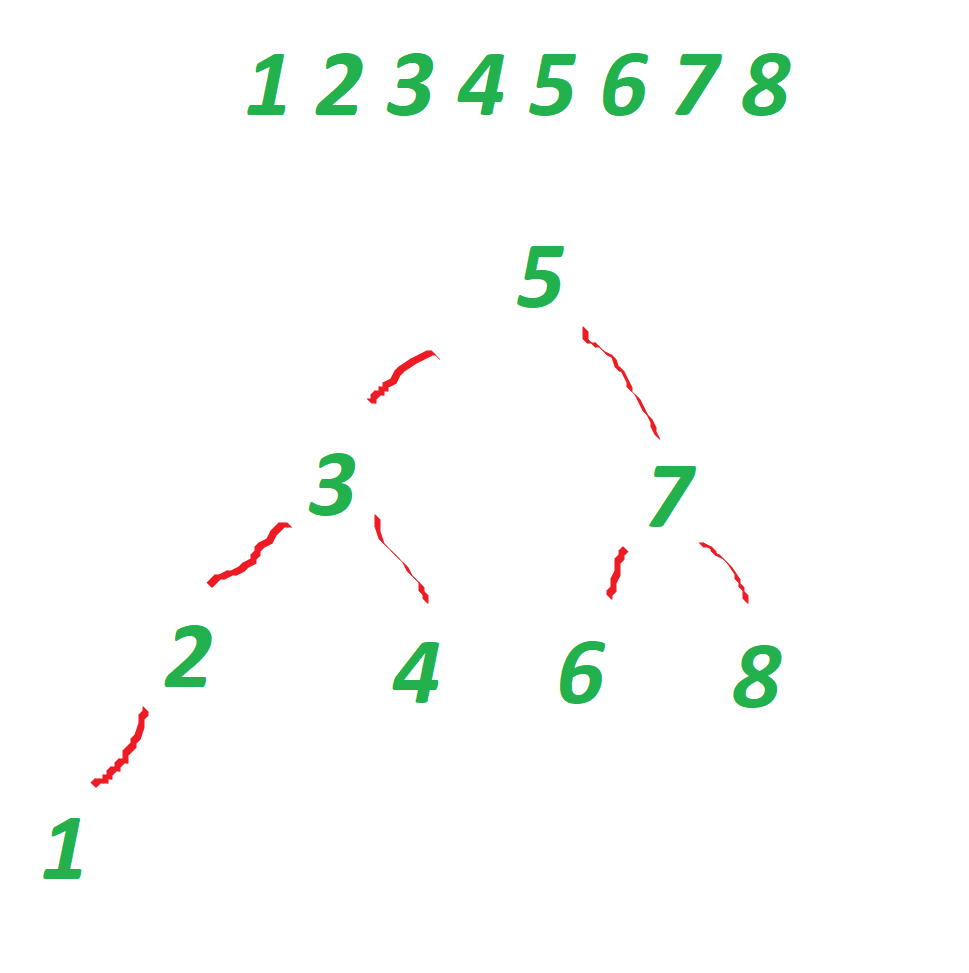
Небольшая подсказка, тому кто попытается это сделать - в первом примере число элементов было специально подобрано так, чтобы не попадать в неопределенность (7 элементов), то есть на каждом шаге кроме последнего из двух элементов, общее число элементов было нечетным. Но в примере выше вы попадете в такую неопределенность при первом разбиении, где вам нужно будет среди {4,5} - выбрать наибольшее.

Соответственно выбрав 5, вы получите два вектора {1,2,3,4} и {6,7,8}.

В первом векторе {1,2,3,4} из {2,3} - снова выбираете 3 и получаете сбалансированное дерево.

Если вы достаточно внимательны, то такая неопределенность не привязана к общему четному количеству чисел и вы с ней встретитесь даже в таком векторе, где общее количество чисел 9 == {1,2,3,4,5,6,7,8,9}

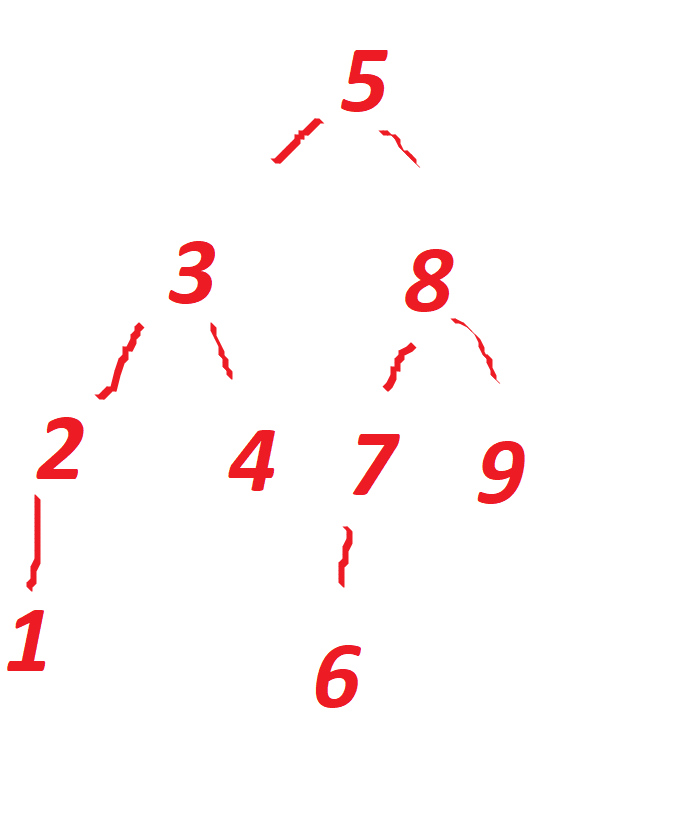
В принципе если суть вы поняли, то рисунок вам не понадобится, но лучше перестрахуемся.

Не воспринимайте этот пассаж, как гайд по деревьям - это ни в коем случае не он, просто нужно осознать принцип оформления этого дерева.

1) Уникальный и сортирующий – std::set

Краткое описание: упорядоченное множество уникальных элементов. Основан на структуре красное-черное дерево и после каждого добавления/удаления элемента сортирует все элементы в порядке возрастания. Благодаря отсутствию уникальных элементов и постоянных сортировок элементы располагаются строго монотонно.
 
Поскольку он постоянно сортирует себя в порядке возрастания – индексы в нем отсутствуют, так как неясно где какой элемент находится, но set гарантирует нам что первый элемент гарантировано меньше [n + C], где C < set.size() - 1, и обратно.

Памятка по функциям:

insert() – добавляет элемент в set, если нету его абсолютной копии.
 
erase(key_number) – удаляет элемент из set’а, поскольку отсутствует доступ по индексу, то erase производит поиск по значению и удаляет элемент в последствии красно-черное дерево пересобирается.
 
find(key_number) – осуществляет поиск по значению в set’е, если key_number не найдено – find() вернет set.end(), в противном случае *find(key_number) == key_number.
 
поиски по диапазону в отсортированном set’е:

lower_bound(key_number) – возвращает итератор на значение, которое меньше чем lower_bound(key_number).
 
upper_bound() – возвращает итератор на значение, которое больше чем upper_bound(key_number).
 
count(key_number) – Возвращает количество элементов равных key_number.

Пример кода не вижу смысла вставлять, функции довольно очевидные, ниже будут примеры с теми на которые стоит обратить внимание при работе с std::set и почти ему подобными.

Операции над множествами:

(1) Пересечение или же S * T = I:

Находит одинаковые элементы в указанных промежутках двух множеств и оставляет один уникальный элемент в новом множестве I. Результат{10, 20, 30}.
 
 set_intersection( S.begin(), S.end(),  T.begin(), T.end(),  inserter(I, I.begin()));

set<int> set1 = {10, 20, 30};
set<int> set2 = {10, 20, 30, 40, 50};
set<int> exposition;
set_intersection(set1.begin(), set1.end(), set2.begin(), set2.end(), inserter(exposition, exposition.begin()));
 
(2) Объединение или же S + T = I:

Берутся 2 множества и добавляются все элементы из двух множеств, далее удаляются дубликаты. Результат{10, 20, 30, 40, 50}.

set_union( S.begin(), S.end(),  T.begin(), T.end(),  inserter(I, I.begin()));
 
 
 
 

//Тут set1 и set2 остались при своих элементах
set<int> set1 = {10, 20, 30};
set<int> set2 = {10, 20, 30, 40, 50};
set<int> exposition;
set_union(set1.begin(), set1.end(), set2.begin(), set2.end(), inserter(exposition, exposition.begin()));

// Более красивый вариант, если позволяет реализация - он быстрее
set<int> set1 = {10, 20, 30};
set<int> set2 = {10, 20, 30, 40, 50};
set1.merge(set2); // после этой операции set2 пустой 

Скорости:

Вставка - O(log n), где n - количество элементов в контейнере.

Удаление - O(log n), где n - количество элементов в контейнере.

upper_bound и lower_bound - O(log n), где n - количество элементов в контейнере.

find(key_number) - O(log n), где n - количество элементов в контейнере.

Пересечение - O(n), где n - общее число элементов в двух контейнерах и оба контейнера одинакового размера.

Объединение - O(n), где n - общее число элементов в двух контейнерах и оба контейнера одинакового размера.


2) У нас появились копии, но мы еще на красно-черном дереве и, возможно, с векторами копий - std::multiset

Краткое описание: благодаря чуду инженерной техники мы получили возможность хранить копии в std::multiset, что невозможно в std::set. Честно ни разу не видел его в чужих решениях на LeetCode и никогда нигде не использовал, мне кажется, что он существует только как реализация хранения копий в красно-черном дереве и если посидеть подумать, то в некоторых ситуациях он будет лучше чем просто std::map.

Если вы его используете и вам нужно получить количество одинаковых элементов, то используйте count(key_number) - в этом лучший.

Можно получить промежуток с помощью:

pair equal_range(const key_type& x)  const – он вернет {i, j} промежуток из значений.

std::multiset<int> mySet = {1, 2, 3, 3, 3, 4};

//вы пробежитесь по дереву и найдете вектор с вашими числами
//собственно, это метод как получить числа из этого вектора
//count() - вернет вам количество этих чисел
auto range = mySet.equal_range(3);

//выводить так
for (auto it = range.first; it != range.second; ++it) {
    if (it != range.first) {
      std::cout << ", ";
    }
    cout << *it;
  }
  cout<<endl;

3) Теперь мы не на красно-черном дереве, а в хэш-мапе - std::unordered_set

Краткое описание: в std::set мы получали постоянно сортирующуюся коллекцию элементов, но в unordered-варианте мы остались без сортировки и оно к лучшему, потому что нам не всегда нужно сортировать элементы - красно-черное дерево лежащее в основе std::set постоянно балансировало и сортировало элементы, чтобы избежать сортировки в основе std::unordered_set лежит хэш-таблица с ключами и значениями, где ключ и значение одно и тоже, только теперь нам не приходится сортировать наш контейнер по возрастанию. Копии тут отсутствуют - не путать с std::multiset.

Горячо приветствую тех, кто дожил до словарей или просто перемотал сюда в поиске нужных ему функций.

Предисловие: хранит если вы решали задачу 1.Two Sum на LeetCode, то одно из наиболее быстрых решений лежит через std::unordered_map и невооруженным глазом видно, что там какая-то игра из значений и итераторов:

Дается вектор целых чисел nums и целое число target, верните индексы двух чисел, которые в сумме дают target.

vector<int> twoSum(vector<int>& nums, int target) {

        unordered_map<int, int> mp;

        for (int i = 0; i < nums.size(); i++) {

            int required = target - nums[i];

            if (mp.find(required) != mp.end()) {

                return {i, mp[required]};

            }

            mp[nums[i]] = i;//совсем не типичная инициализация

        }

        

        return {-1, -1};

    }

mp[nums[i]] = i; - В данном варианте, внутри unordered_map<int>mp происходит следующее:

nums[i] - становится ключом данного элемента mp.
i - становится значением.

ВНИМАНИЕ: nums[i] - это ключ, а i - это значение, если мы находим ключ, то возвращаем индекс - так как этого требует задача, и не имеет смысла делать наоборот, так как по значению вы ключ не найдете. Перечитайте условие задачи, если запутались.

функция find() - производит поиск по ключу, а именно не по текущему индексу i - значение, а по nums[i] добавляемому в качестве ключа.

Если попросить значение у mp[nums[i]] - мы получим итератор числа при складывании которого с еще одним любым числом - мы получим искомый target.

Я думаю найдутся люди, которые не знают почему возвращаемое значение в {}.

Вспомните инициализацию вектора из первой части {1,2,3} - вот это она есть, только местечковая и не факт, что это вектор.

В C++ присутствует такой класс как std::pair - пара значений и такой вызов {1,2} - может считаться как пара, поэтому нужно смотреть на возвращаемый тип функции. Не может быть пары из 3-ех значений, но может быть такая сигнатура pair<int, pair<int, int>>, тогда возвращаемое значение будет выглядеть так {int, {int, int}};

Кстати если вы хотите вернуть двумерный вектор в таком виде или прочитать его, то получите что-то около этого {{1,2,3}}, то есть у вас получится 1 строка и 3 столбца, но все зависит от того как это выводить.

Собственно - это все, что вам нужно знать про данный тип ассоциативных контейнеров, остальное расскажу далее.

1) я хочу хранить, удалять, вставлять и находить - быстро и сразу: std::map

Краткое описание:  В его основе лежит бинарное дерево, где элементы лежащие в этом дереве - это ключи(Разбирать также как с std::set считаю нецелесообразным). хранит пары ключ-значение, где ключи уникальны и отсортированы по возрастанию. Благодаря такой системе очень быстро позволяет вставлять и удалять элементы, производя поиск по ключу.
Ключи в std::map уникальны и элементы сортируются по ключу.

Памятка по функциям:

3 варианта insert() - добавляет элемент:
1)insert(std::make_pair(ключ, значение))
2)insert({ключ, значение})
3)map[ключ] = значение;

erase(ключ) - удаляет элемент по ключу.

find(ключ) - производит поиск по ключу, если подзабыли, то перечитайте разбор первой задачи в предисловии.

В случае, если элемент не найден возвращает итератор на map.end():
if (mp.find(required) != mp.end()) - здесь происходит проверка на наличие элемента по ключу, а именно проверка наличие разности target - nums[i] в нашем map.

size() - возвращает реальный размер.

Ключи ни в коем случае не являются размером вектора, да вы можете занумеровать их от нуля до n, но это не размер.

count(ключ) - производит поиск на наличие элемента с заданным ключом.

Если число существует, то возвращает 1, если нет, то 0.

if (map.count(1000) > 0) - так выглядит обычная проверка на наличие элемента.

Скорости:

Вставка - O(log n), где n - количество элементов в контейнере(может быть выше из-за дерева).

Удаление - O(log n), где n - количество элементов в контейнере(может быть выше из-за дерева).

find(key_number) - O(log n), где n - количество элементов в контейнере(может быть выше из-за дерева).

2) Теперь по одному ключу мы можем хранить несколько значений по одному ключу - std::multimap

Краткое описание: Создается бинарное дерево и к одинаковому ключу создается вектор из значений. Ключи в std::map уникальны и элементы сортируются по ключу.

Функции абсолютно такие же, но остается вопрос как получить несколько значений по одному ключу?

multimap<int, int> multimap;
multimap.insert({1, 100});
multimap.insert({1, 200});
multimap.insert({1, 300});
multimap.insert({1, 400});
multimap.insert({1, 500});

// Получаем диапазон с ключом 1
auto range = multimap.equal_range(1);

// Вывод
for (auto it = range.first; it != range.second; ++it) {
  cout << it->second << endl;
}

С функцией equal_range() мы уже встречались когда говорили выше про std::multiset

3) Ключи уникальны, но они не сортируются, хотя правильнее сказать - std::unordered_map

Краткое описание: встречались поскольку сортировки ключей нету, то там они лежат в порядке того как вы заполняете его и зависит от такого, как вы их удаляете, то есть прямое хэширование и никаких бинарных деревьев внутри него нету. Ключи полностью уникальны и вызов функции equal_range(ключ) - вернет одно значение.

Скорости:

Вставка - O(log n), где n - количество элементов в контейнере.

Удаление - O(log n), где n - количество элементов в контейнере.

find(key_number) - O(log n), где n - количество элементов в контейнере.

Спасибо тем, кто дочитал.