Во все времена люди пытались найти способ безопасной передачи информации, метод, при котором зашифрованное сообщение мог прочитать только тот, кому оно было адресовано. В современном мире шифры используют повсюду: от мессенджеров и банков до блокчейнов. Происходит непрекращаемое улучшение алгоритмов шифровки: создаются новые методы, находятся уязвимости в прошлых решениях.
Предлагаю рассмотреть разные методы шифрования и проследить за их развитием на протяжении нескольких тысяч лет.
Атбаш
Атбаш — простой шифр подстановки, который можно встретить в священных иудейских книгах VI век до н. э. Правило шифрования состоит в замене i-й буквы алфавита буквой с номером , где
— число букв в алфавите. Пример для латинского алфавита выглядит так: при исходном тексте abcdefghijklmnopqrstuvwxyz шифр будет таким — zyxwvutsrqponmlkjihgfedcba.
Безусловно, такой алгоритм нельзя назвать надежным. Человеку, желающему узнать переданную информацию, необходимо было лишь знать, какой алгоритм использовал шифровщик. Используя эти знания, он мог с легкостью расшифровать сообщение.
Шифр Цезаря
Суть алгоритма заключалась в сдвиге алфавита на целое количество символов (для алфавита а,б,в…,ю,я при сдвиге на 1 символ вправо результат был бы — я,а,б...,ю).
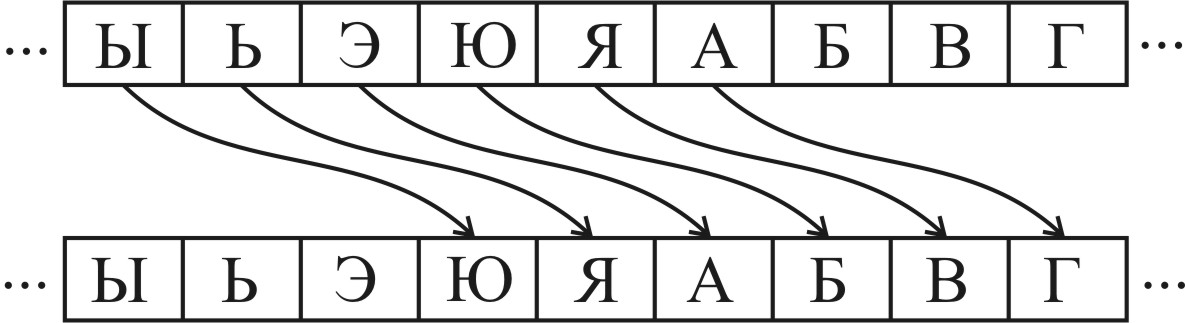
Стоит признать, что этот метод был уже менее тривиальным. Несмотря на это, третья сторона, зная, что вы использовали шифр Цезаря, могла расшифровать сообщение, перебрав разные «сдвиги» — даже вручную это не занимало много времени. Что дальше?
Пляшущие человечки и другие алгоритмы сопоставления букв символам/знакам
При переборе «в лоб» мы имеем нерешаемую задачу, так как приходится перебирать порядка вариантов (если брать 30 букв за средний размер алфавита) — на первый знак есть 30 вариантов заменяемой его буквы, на второй знак — 29 букв и так далее; то есть
. Это огромное число, которое с трудом обработает даже современный компьютер. Казалось бы, рабочий алгоритм!

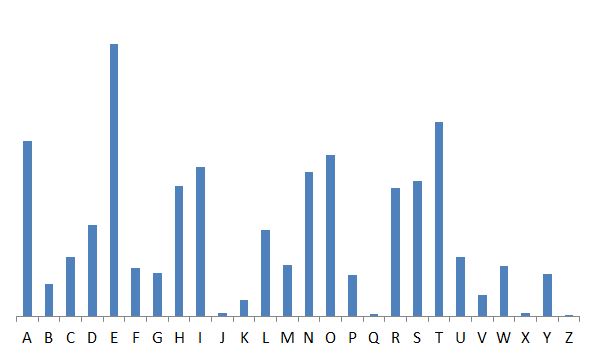
Но лингвистика и статистика тоже не стояли на месте: появился такой термин, как «число вхождений» буквы в текст. Соответственно, впервые расшифровав букву «а» или «о», мы знаем, как расшифровать ее еще несколько десятков раз в тексте. Это позволило значительно сократить величину перебора вариантов (уже не , а гораздо меньше).
Улучшенное сопоставление букв символам/знакам
Решили, что можно производить шифровку, заменяя не одну букву, а сочетание из двух-трех-четырех. Например — ab = @, bc = #, ac = $ и так далее. Ну и в чем здесь проблема?
Оказалось, что в этом способе было несколько несовершенств: во-первых, алгоритм был не таким удобным в использовании: процесс шифрования и расшифровки значительно усложнился. Во-вторых, статистический анализ текста, описанный в прошлом методе, давал возможность расшифровывать и этот алгоритм.
На помощь пришла теория чисел
Для начала предлагаю вспомнить ту математическую базу, которая понадобится для понимания процессов шифровки: о чем гласит теорема Эйлера и Эйлерова функция? Для составного числа можно посчитать функцию
, вычисляющую количество различных натуральных чисел, не превосходящих
и не имеющих общих делителей с
; так вот,
для всех
, взаимно простых с
— так и выглядит теорема Эйлера. Разбираемся дальше: если
— произведение
и
, то справедливо утверждение о том, что
— назовем эту величину
. Попытаемся подобрать два числа
и
так, чтобы
при t — любом целом числе.
Начинается магия — процесс шифрования
Как же в действительности все описанное работает? Предположим, нам необходимо безопасно передать другу важное послание. В первую очередь нужно, чтобы человек, который намерен переслать нам информацию, знал два числа: и
(эти данные можно передать как угодно — в любом мессенджере, например). Назовем передаваемую информацию буквой
. И дальше говорим отправителю, используя
, посчитать
, равное
и сообщить нам результат. Отлично,
мы знаем.
Внимательно следите за математикой: . Значит, посчитав остаток от деления
на
, мы узнаем исходную информацию. Соответственно, если мы возьмем
и
такими, чтобы
было громадным 700-значным числом, то алгоритм нам позволит «резать» информацию на части по 2 килобита информации. Круто, да?
Алгоритм RSA
Описанная мною математика — это то, как работает самый популярный в современном мире алгоритм шифрования RSA, который является одним из первых асимметричных алгоритмов.
Даже если мы открытым образом передаем информацию об и
, человеку, перехватившему эти данные, необходимо знать
, чтобы найти
. А для того чтобы посчитать
, ему нужно разложить на множители гигантское число
— а это не такая простая задача, как кажется. Еще не существует алгоритмов, способных разложить на множители 700-значное число за разумное время.
Подводя итог по RSA, не умея разложить на простые множители, вы никогда не сможете найти
и расшифровать информацию.
Применение шифрования в блокчейне
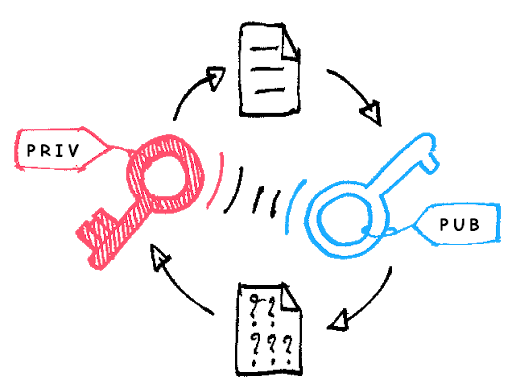
На мой взгляд, блокчейн — это вершина шифрования, так как децентрализация подразумевает под собой постоянное использование алгоритмов шифрования данных. Разберем один из примеров шифровки: при создании нового криптовалютного кошелька генерируется пара ключей (открытый и закрытый ключ). Для чего это нужно? С одной стороны есть публичный адрес, который генерируется с использованием открытого ключа и может безопасно передаваться другим; с другой стороны используется закрытый ключ для создания цифровых подписей и проверки транзакций. Как только транзакция была подтверждена путем валидации хэша, содержащегося в цифровой подписи, эта транзакция может быть добавлена в блокчейн-регистр.
Эта система проверки цифровой подписи гарантирует, что только лицо, у которого есть закрытый ключ, связанный с соответствующим криптовалютным кошельком, может выводить из него средства.

Заключение
Конечно, те алгоритмы, которые мы разобрали в этой статье — это далеко не всё, что придумало человечество. Я обошел стороной развивающийся алгоритм Elliptic Curve Digital Signature Algorithm (Алгоритм Цифровой Подписи Эллиптической Кривой, ECDSA), который может посоревноваться с RSA во многих аспектах. Но эллиптические кривые — это отдельная тема с суровой математикой и множеством нюансов.
Математика повсюду! Задумайтесь: математические теоремы, сформулированные в 17-18 веках, нашли свое применение через сотни лет в банковских системах, современных базах данных. И все эти системы можно взломать, лишь понимая, как устроены простые числа!
Комментарии (12)

ferumcl
29.08.2023 07:35Не совсем понял про
- почему именно так считается в третьем пункте?

derlugov Автор
29.08.2023 07:35Представьте, у нас есть алфавит из 30 букв и есть 30 символов, каждый из которых заменяет определенную букву. На первую букву есть 30 символов, которые могут заменить ее; на вторую букву остается 29 вариантов замены (так как 1 символ мы уже заняли). И так далее.
По сути, это число перестановок 30 символов - почитайте про это.
Советую вам ознакомиться с основами комбинаторики. Например, у Виленкина есть прекрасная книжка по этой теме. Я читал ее в бумажном формате, но есть и в электронном виде.

ferumcl
29.08.2023 07:35Интересно. Какие еще книги по математике можете посоветовать?

derlugov Автор
29.08.2023 07:35Конечно, все зависит от преследуемых целей. Для введения в математику могу посоветовать книжку Алексея Савватеева «Математика для гуманитариев» - она не для гуманитариев, просто материал изложен простым языком)
Если хочется почитать про прикладную математику, возьмите «Числа и фигуры» или комбинаторику Виленкина.Для глубокого погружения в теорию чисел всегда мне советовали Алфутову. Действительно, хорошая книга. Ну, а если целью является «нарешивание» задачек, тогда рекомендую сборники Шабунина, Сканави, Ткачука.
Как видите, четкого ответа дать не получилось))

ferumcl
29.08.2023 07:35Большое спасибо! Ознакомлюсь со всем.
Подскажите, а по алгоритмам что интересного есть?

derlugov Автор
29.08.2023 07:35По алгоритмам рекомендую посмотреть цикл лекций Тимофея Хирьянова - преподавателя МФТИ. Лекции в открытом доступе можно найти
По книгам точно сказать не могу. Давно еще читал «Олимпиадное программирование» Антти Лааксонена. Честно говоря, не очень понравилась


vilgeforce
По части RSA принято использовать другие обозначения, а именно: p, q, n, d, e
derlugov Автор
Спасибо, учту это