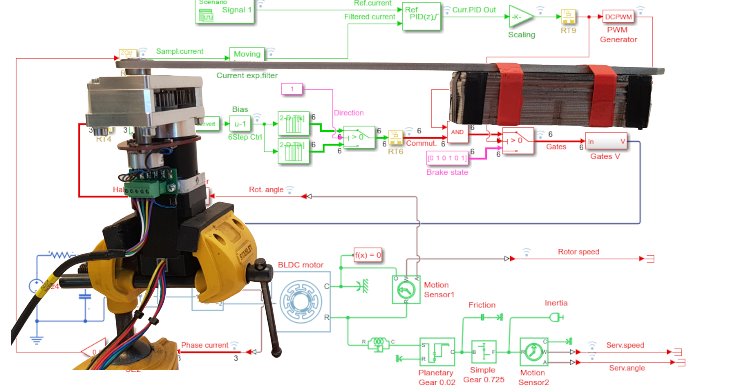
Продолжаем открытый проект сервоконтроллера MC50. 

В предыдущей статье была разработана архитектура управления и написана программа сервопривода. Но регулятор был вручную настроен на определенный тип нагрузки. А что делать если тип и динамика нагрузки неизвестны?

Предыдущие статьи по теме проекта MC50

• Схема и плата контроллера

• Первые шаги по программированию контроллера

• Развёртывание промежуточного программного обеспечения

• Отладка взаимодействия с интернетом

• 6-шаговая коммутация BLDC моторов

• Разработка сервопривода с BLDC мотором

В борьбе за робастность все средства хороши. Пробуем варианты и на реальном сервоприводе и на модели. При работе с железом можно за деревьями не увидеть леса. Т.е. за шумами и нелинейностями сенсоров и драйверов, мелкими багами в таймингах и гонках задач можно не увидеть действительно эффективные алгоритмы. Поэтому первым делом отдаём предпочтение разработке обобщённых моделей и симуляции, а потом уже проверке в железе.

В данном случае управляем низкоскоростным сервоприводом имеющим довольно инерционную нагрузку с люфтом и торсионной гибкостью. Торсионная гибкость вызывается в редукторе первой ступенью, поскольку в ней использованы пластиковые шестерни. Пластик имеет свойство сильно деформироваться. С одной стороны такое исполнение защищает от разрушения зубьев шестерён при ударных вращательных воздействиях на вал сервопривода. С другой стороны это сильно усложняют качественное управление скоростью вращения.

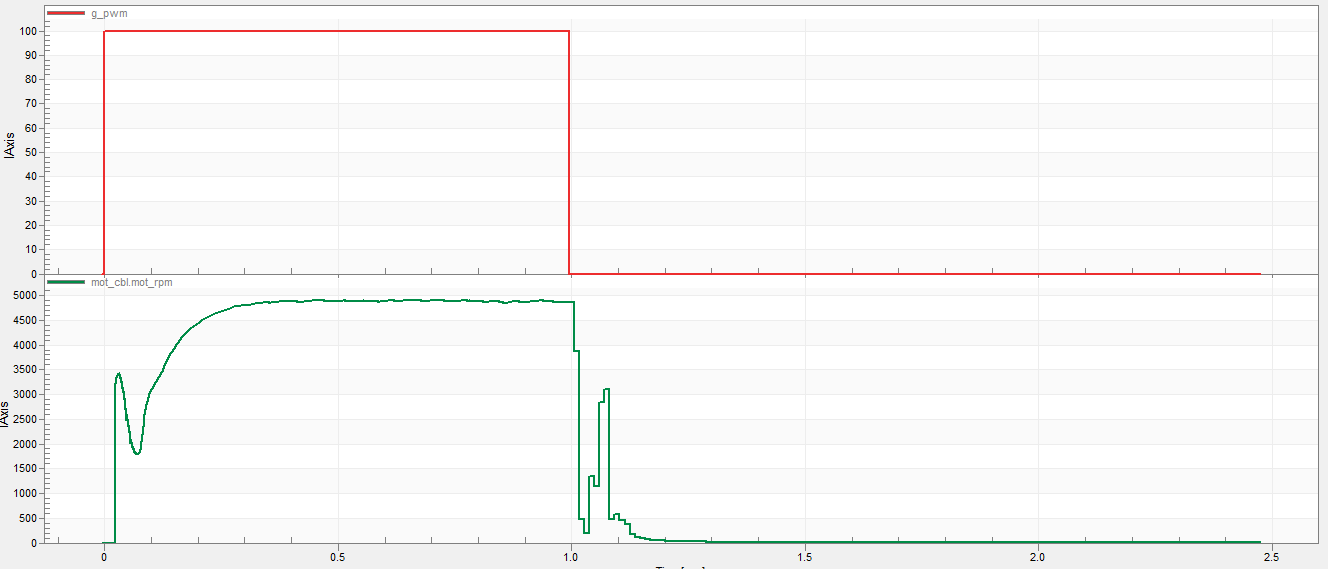
Начинаем с измерения реальной динамики скорости вращения ротора при подаче импульса полного напряжения (заполнение ШИМ 100%, т.е. модуляция отсутствует). Первое измерение с торможением обмотками и второе измерение без торможения обмотками. Измерение без торможение понадобилось чтобы лучше оценить инерцию системы. 

Как переносить данные из платы контроллера в MATLAB

В файле MC50_FreeMaster.pmpx находится проект FreeMaster предназначенный для снятия на PC графиков внутренних сигналов сервоконтроллера. 

Как это делается на анимации ниже

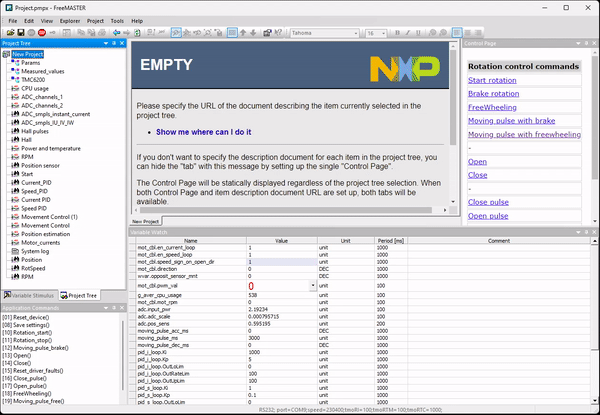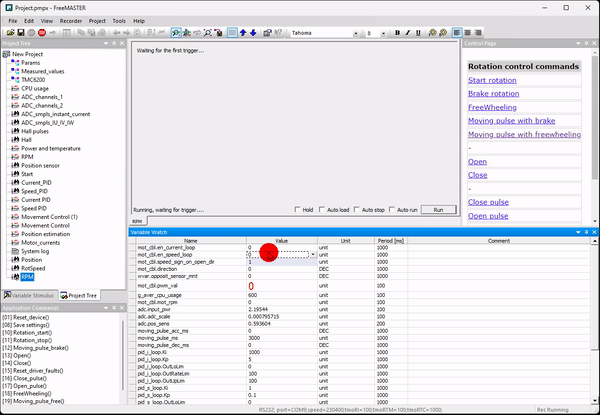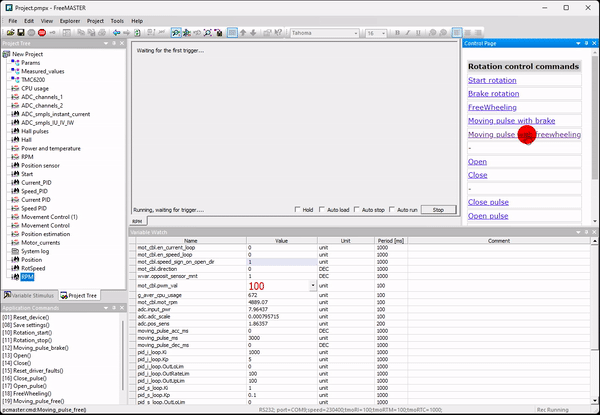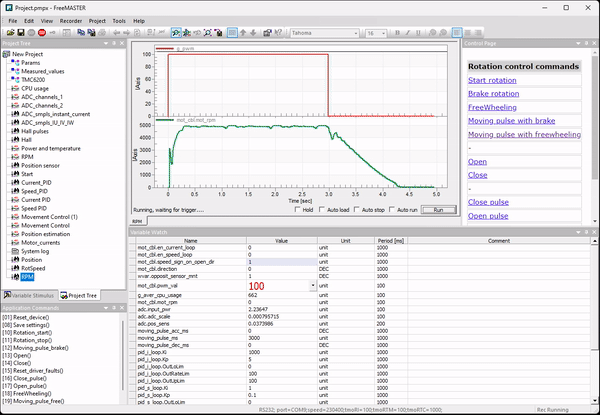
График переносится в MATLAB с помощью такого скрипта :

fmstr = actxserver ('MCB.PCM');
fmstr.GetCurrentRecorderData;
recdata=cell2mat(fmstr.LastRecorder_data);
recnames=fmstr.LastRecorder_serieNames;
fmstr.ReadVariable('adc.adc_scale');
adc_scale = fmstr.LastVariable_vValue; % Получим масштаб напряжения на АЦП
fmstr.ReadVariable('mot_cbl.pwm_freq');
pwm_frquency = fmstr.LastVariable_vValue; 
fmstr.GetCurrentRecorderData;
recdata=cell2mat(fmstr.LastRecorder_data);
recnames=fmstr.LastRecorder_serieNames;
smpls_num = length(recdata);
st= 10/pwm_frquency;
stop_time = st*smpls_num;
recdata = transpose(recdata);
x = transpose(linspace(0, st*(smpls_num-1),smpls_num ));
recdata = horzcat(x,recdata);
pwm_data = recdata(:,2);
speed_data = recdata(:,3);
scrsz = get(groot,'ScreenSize');
figure('OuterPosition',[1 50 scrsz(3) scrsz(4)-50]);
n = length(recnames);
ax = subplot(2,1,1);
plot(ax, x, pwm_data);
ax = subplot(2,1,2);
plot(ax, x, speed_data);

Скрипт находится в файле Import_from_FreeMaster_PWM_Speed.m

Создание адекватной модели

Рабочих моделей может быть создано много. Здесь приходится искать компромиссы. Сильно детализированные модели выполняются слишком медленно (десятки минут на одну секунду реального времени для модели с шагом в 0.1 мкс с точной моделью мотора и инвертора). Для ускорения вычислений модели приходится упрощать, но тогда теряется точность результата.  Простые модели используются для концептуального выбора и тюнинга системы управления. Детализированные модели используются для верификации.

Детализированная модель 6-шагового управления с механикой, инвертором и мотором

Вначале строим модель с точной по возможности структурой механической части (Servodriver_identification.mdl) Здесь учтены: торсионная гибкость, момент инерции, сухое и вязкое трение. Планетарный редуктор представлен двумя ступенями. Первая ступень пластиковая, вторая выполнена из металла, поэтому после первой ступени уже нет компонента торсионной гибкости.  В модели симулируется подача максимального скачка напряжения на мотор. В ответ тот начинает вращаться в режиме 6-шаговой коммутации. Через некоторое время напряжение в модели снимается и на графике наблюдаем спад скорости вращения до нуля.

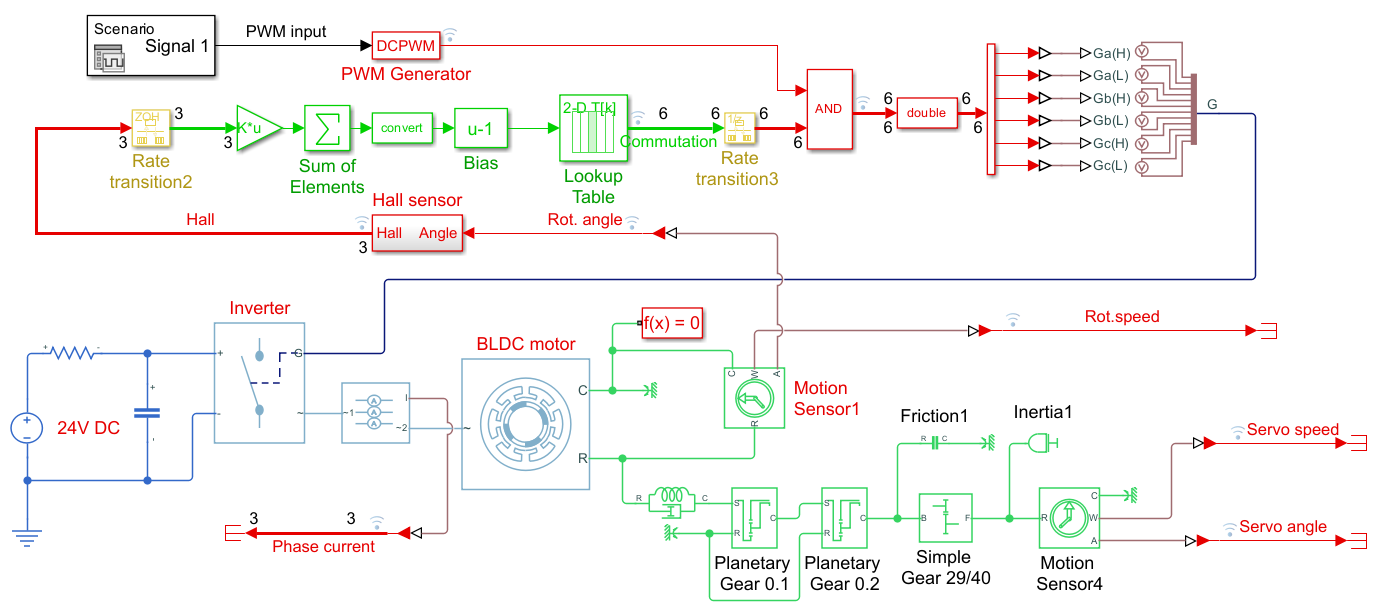
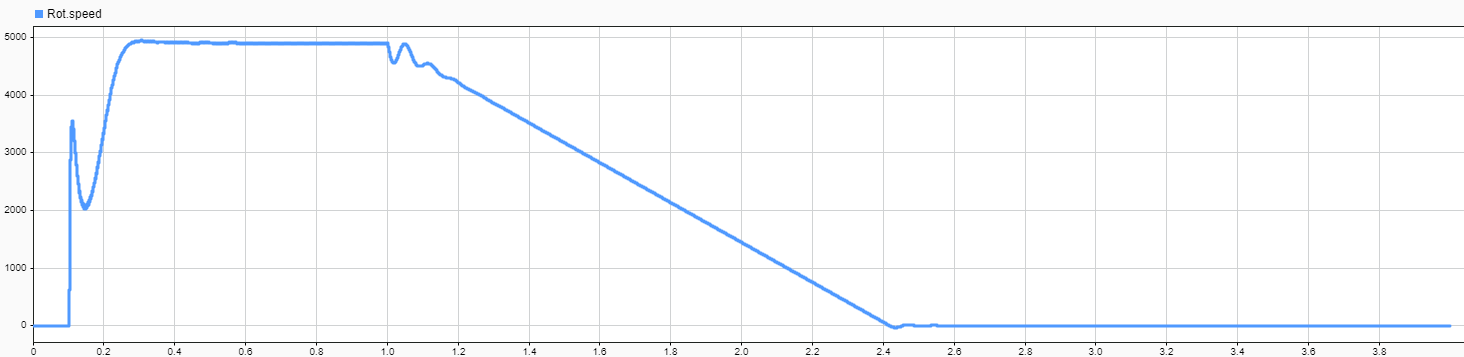
Регулировкой параметров механических компонентов добиваемся наилучшего совпадения с реальным графиком отклика скорости вращения ротора на импульс полного напряжения. 

Модель получилась медленная. Поэтому её упрощаем заменив редуктор на базовые элементы гибкости и трения. Получилась следующая модель (Servodriver_simple_PMSM.mdl): 

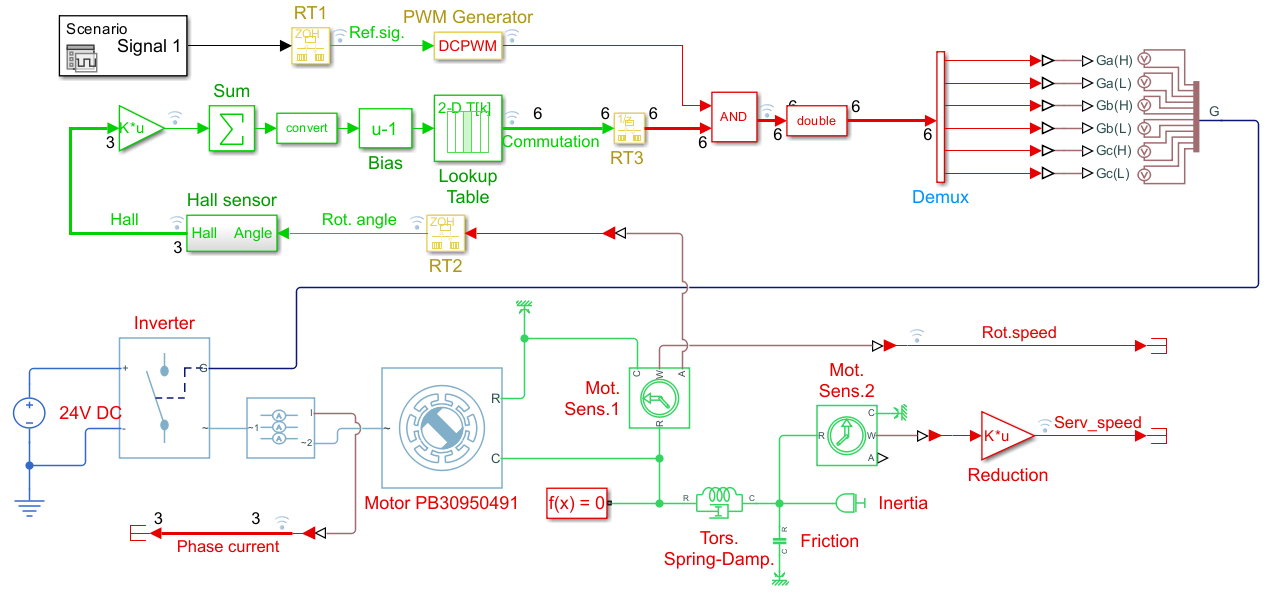
Построена вроде бы неплохо совпадающая с экспериментом модель, но она не годится для автоматического тюнинга систем управления в MATLAB. Её надо линеаризовать.  Но в модели драйвера много нелинеаризуемых элементов. Неплохо бы заменить целиком драйвер, мотор и механическую систему одним блоком переходной характеристики управляемой системы. Это на порядок повысило бы скорость симуляции, а главное дало возможность автоматически тюнинговать PID-ы или иные виды компенсаторов .

Концептуальная линеаризованная модель привода

Стремимся упростить модель до такого уровня, где концептуально могли бы сравнивать разные архитектуры управления не отвлекаясь на мелочи реализации 

Сначала упрощаем модель до такого вида

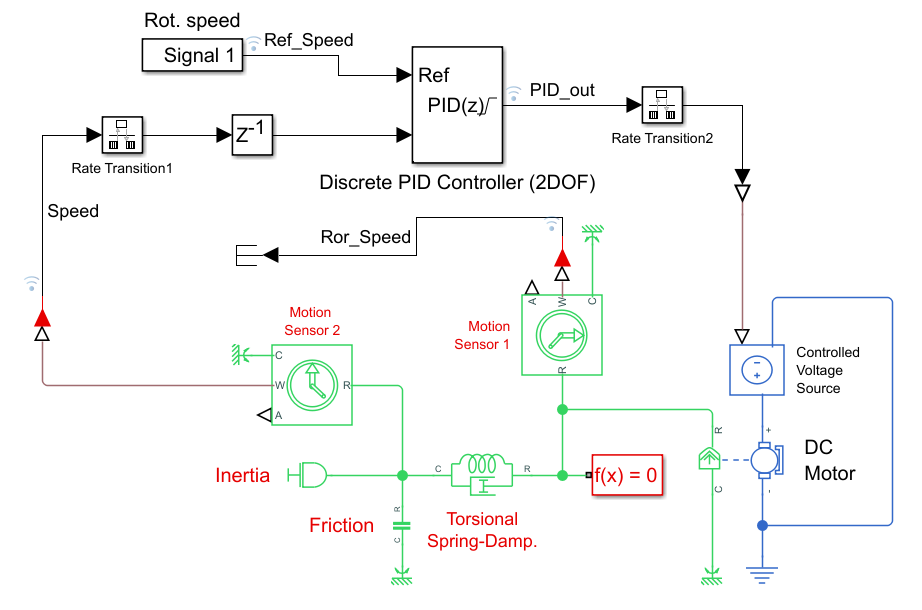
Здесь BLDC и все 6-шаговое управление упрощаются до двигателя постоянного тока управляемого напряжением. Без ШИМ, коммутатора и прочих деталей. Добиваемся отклика модели аналогичного реальному, как в предыдущей модели.  

Далее мотор и всю механику попытаемся заменить одной переходной характеристикой n-ого (пока не ясно какого) порядка. Для этого воспользуемся приложением MATLAB под названием System Identification. 

В файле Pulse_w_hard_stop_workspace.mat находятся все данные после импорта одной из записей сигнала отклика скорости вращения ротора на импульс полного напряжения с использованием торможения закорачиванием обмоток. 

Прежде чем приступить к идентификации немного преобразуем исходные записи сигналов. Во-первых, уберём паузу перед подачей полного напряжения. Во-вторых, уберём мёртвую зону в самом начале записи скорости, когда ротор не сделал полный оборот и данные о скорости недоступны. 

Заменим эту зону кубическим сплайном, как показано в скрипте ниже: (Файл скрипта Conditioning.m)

st_indx =find(pwm_data >0);
pwm_data = pwm_data(st_indx:size(pwm_data));
speed_data = speed_data(st_indx:size(speed_data));
% Убираем начальный участок для компенсации задержки измерения скорости
n =find(speed_data >0);
n = n(1);
aver_rpm=speed_data(n)/2;
hall_step_duration = 1/((aver_rpm/60)*24);
hall_meas_delay = hall_step_duration*12;
k = round(hall_meas_delay/st);
pwm_data = pwm_data(k:size(pwm_data));
speed_data = speed_data(k:size(speed_data));
n =find(speed_data >0);
n = n(1);
% Подменяем начальную часть графика скорости кубическим сплайном компенсируя
% неточность измерения
x = [-1 0 n-1];
y = [0 0 speed_data(n)];
xx = linspace(0,n-1,n-1);
st_spline = csapi(x,y,xx);
st_spline = st_spline';
speed_data = speed_data(n:size(speed_data));
speed_data = vertcat(st_spline, speed_data);
smpls_num = size(pwm_data,1);
stop_time = smpls_num*st;
clear st_spline xx x y n k hall_step_duration hall_meas_delay aver_rpm st_indx

Если не преобразовать таким образом сигнал, то идентификация даст сильно искажённую оценку.  

Идентификация системы

Готовая сессия идентификации находится в файле Identification_session.sid

Как загрузить сессию идентификации показано здесь:

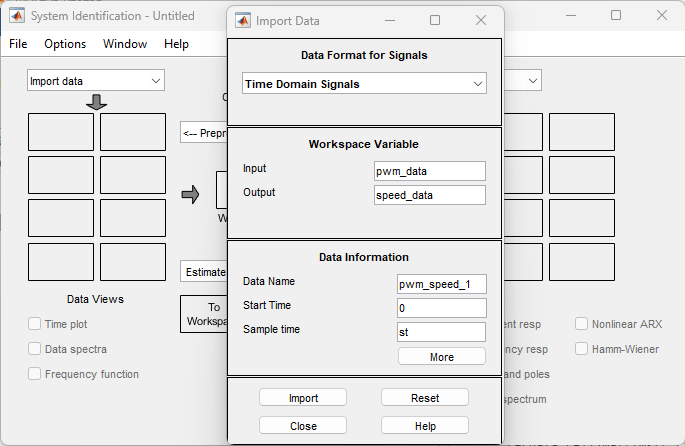
Если начинать идентификацию с нуля, то импортируем данные из рабочего пространства

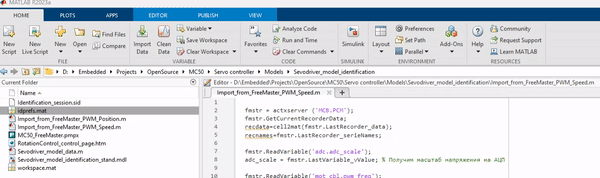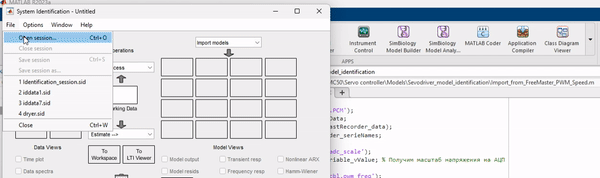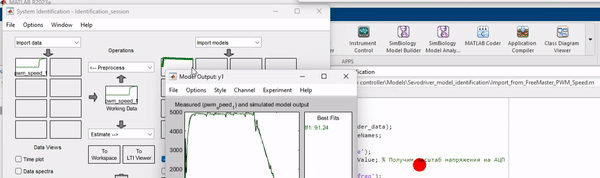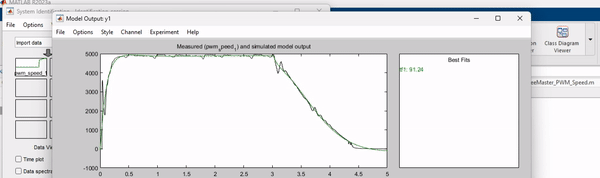
Идентифицируем  методом Transfer Function Models, поскольку сильных нелинейностей не ожидается.

Хорошие результаты показала идентификация функций передачи 7-го порядка с 4 и 5 нулями. 

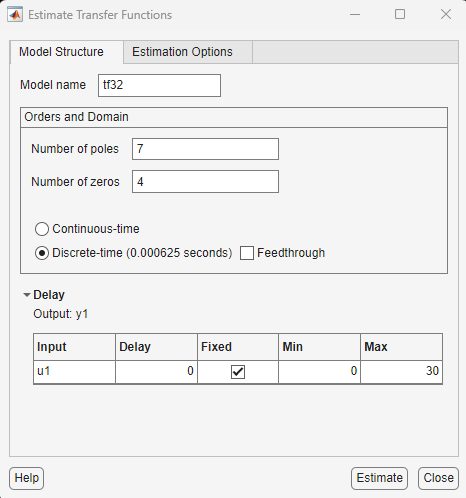
Выбираем характеристику 7-го порядка с 5-ю нулями. Порядок характеристики на первый взгляд кажется завышенным и присутствуют явно лишние артефакты в графике реакции на скачок управляющего воздействия.

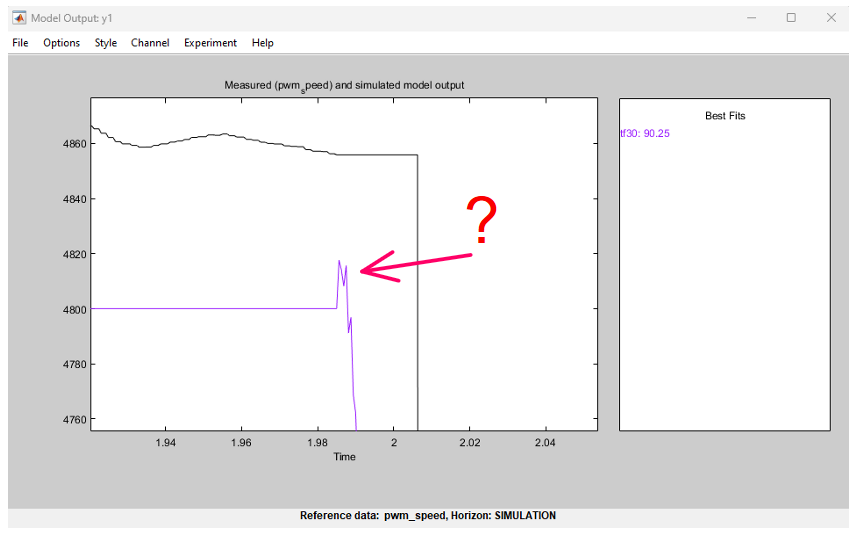
В этом случае можем воспользоваться приложением MATLAB под названием  Model Reducer. 

Экспортируем найденную переходную характеристику с названием tf в рабочее пространство MATLAB и загрузим её в Model Reducer.

На диаграмме нулей и полюсов отрезаем далеко ушедшие полюса и нули

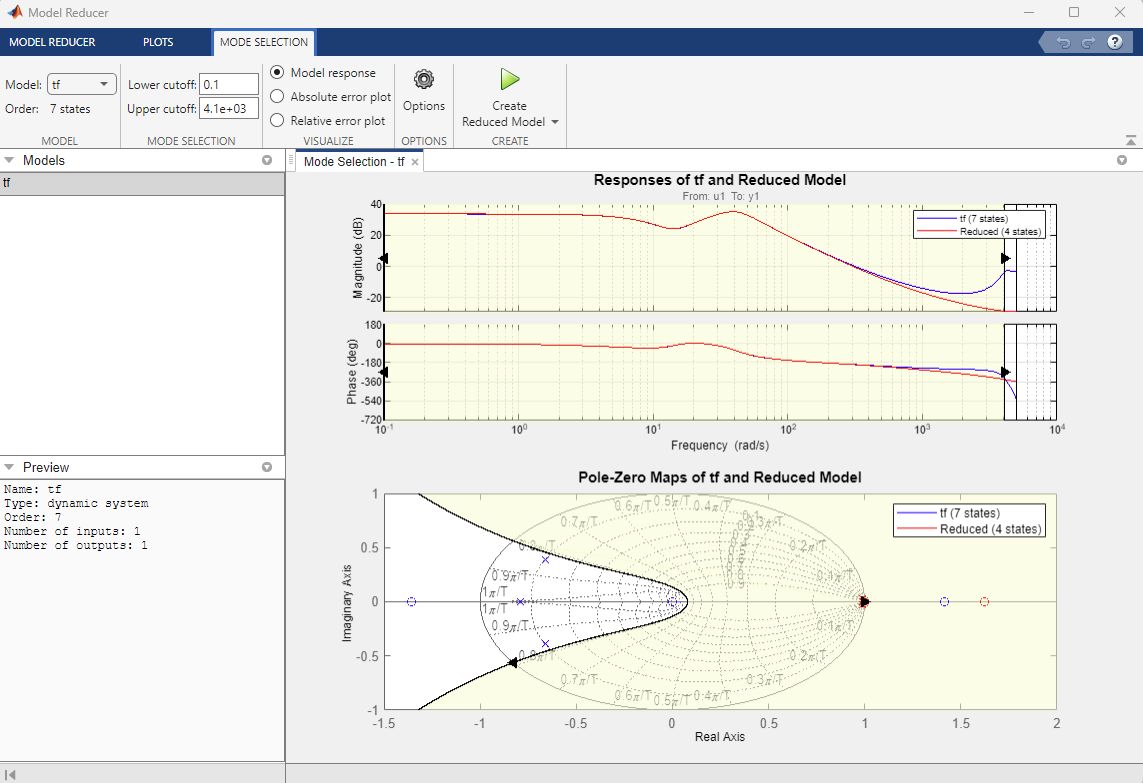
Получаем в результате модель 4-го порядка без лишних артефактов на переходной характеристике. 

Сессия Model Reducer находится в файле ModelReducerSession.mat

Экспортируем модель с названием tf_simple  в рабочее пространство MATLAB.

Перепроверка идентифицированной модели

Для перепроверки идентифицированной переходной характеристики была создана простая модель.

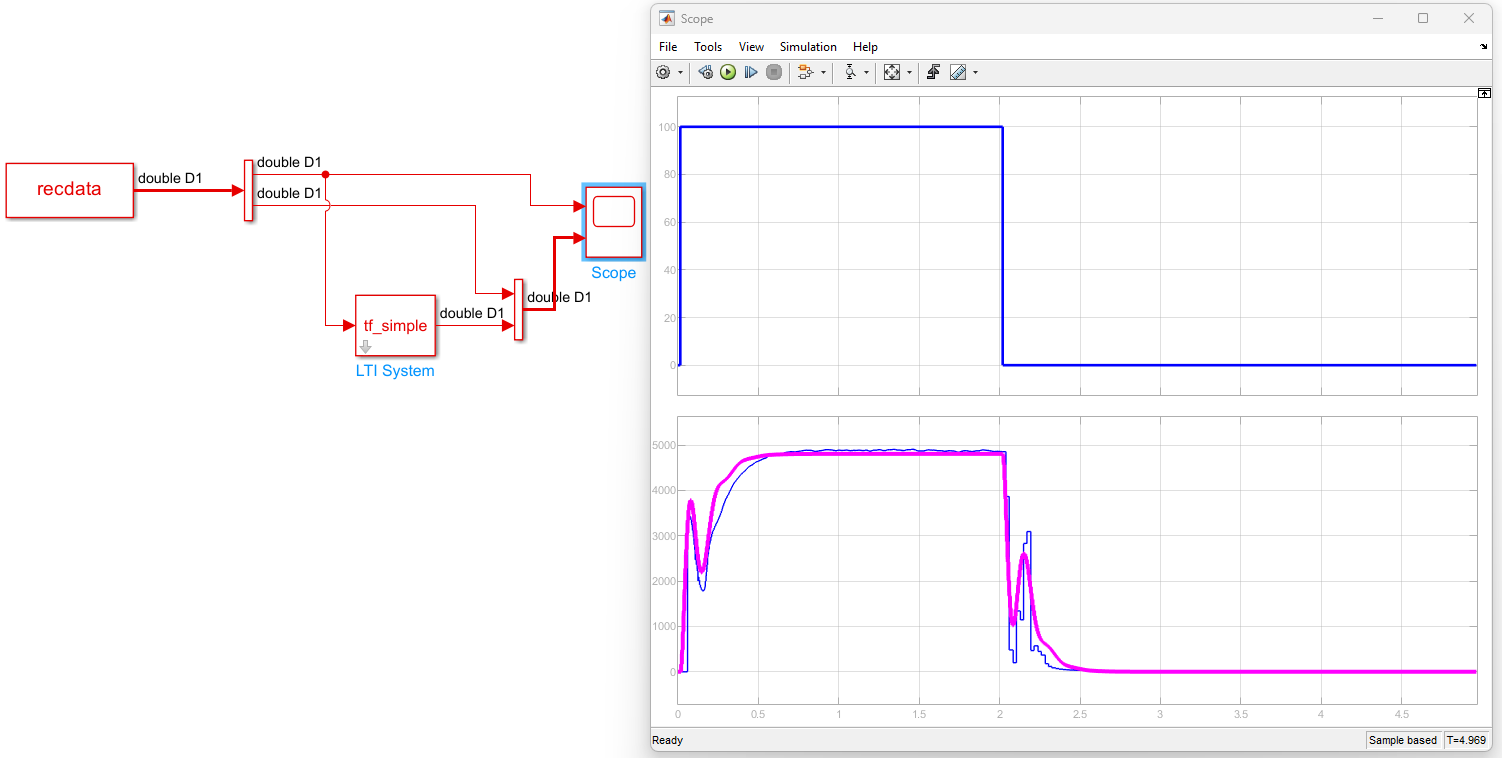
Модель сравнивает реальный отклик записанный с платы и отклик идентифицированной и редуцированной переходной характеристики. Отклики довольно схожи. Переходную характеристику принимаем в работу. 

Простейшая модель

Идентифицированная переходная характеристика позволяет построить простейшую модель системы управления скоростью ротора мотора сервопривода. 

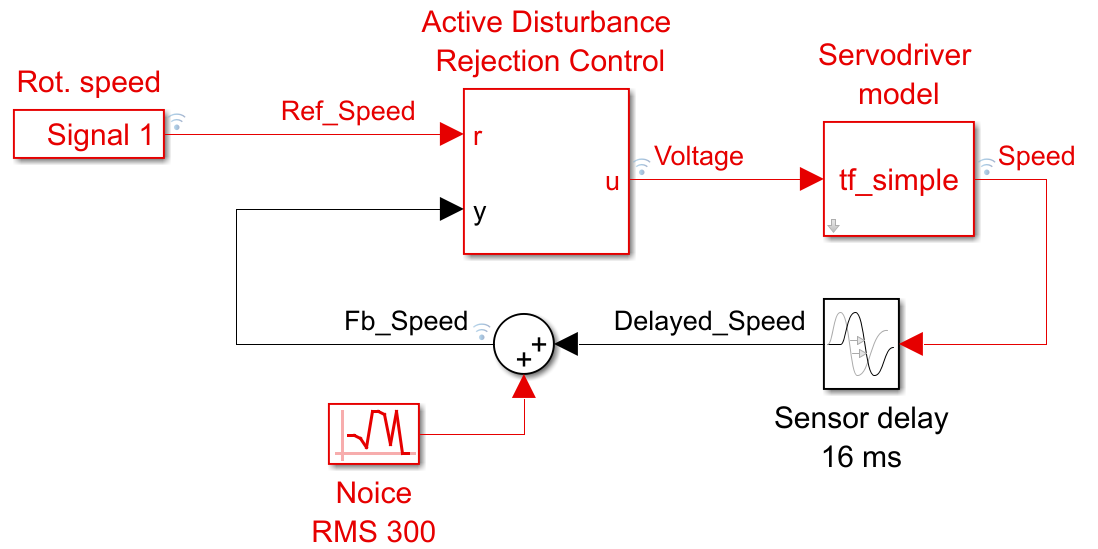
Блок Sensor delay имитирует задержку показаний измерения скорости вращения. Примем её равной 16 мс. Такую задержку создаёт экспоненциальный цифровой фильтр в тракте измерения скорости вращения выходного вала. У датчиков холла задержка измерения скорости вращения зависит от самой скорости вращения. На максимальной скорости она будет равна приблизительно 12 мс.  Фильтры необходимы поскольку скорость вычисляется по разнице отсчётов, которая даёт слишком большой уровень шума . 

Блок Noice имитируем шум получаемый в показаниях скорости вращения после фильтрации.   

Коэффициенты блока PID могут быть автоматически настроены при нажатии на кнопку Tune…

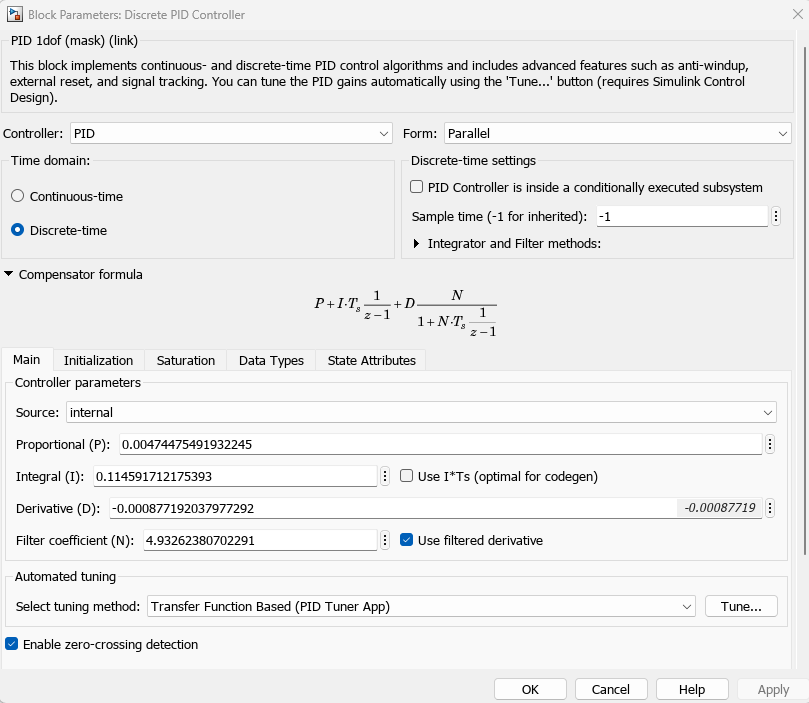
Если найденные коэффициенты не устраивают, их можно подстроить вручную. Подстройка ведется не самих коэффициентов, а целей регулирования. Это принципиально отличает процесс тюнинга от простого перебора коэффициентов. 

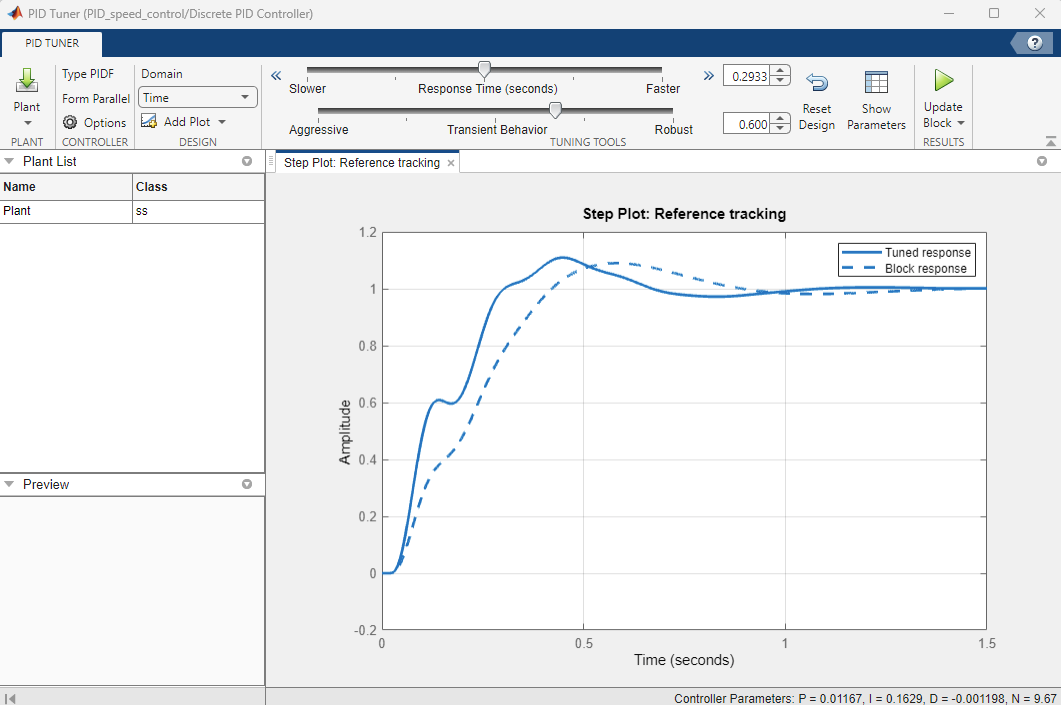
Здесь обнаруживаем, что робастность вступает в прямое противоречие со скоростью реакции. Это очень характерное и неизбежное свойство PID регуляторов.

Применяя инструмент PID tuner удалось получить такое компромиссное решение между амплитудой выбросов, робастностью и скоростью нарастания отклика.

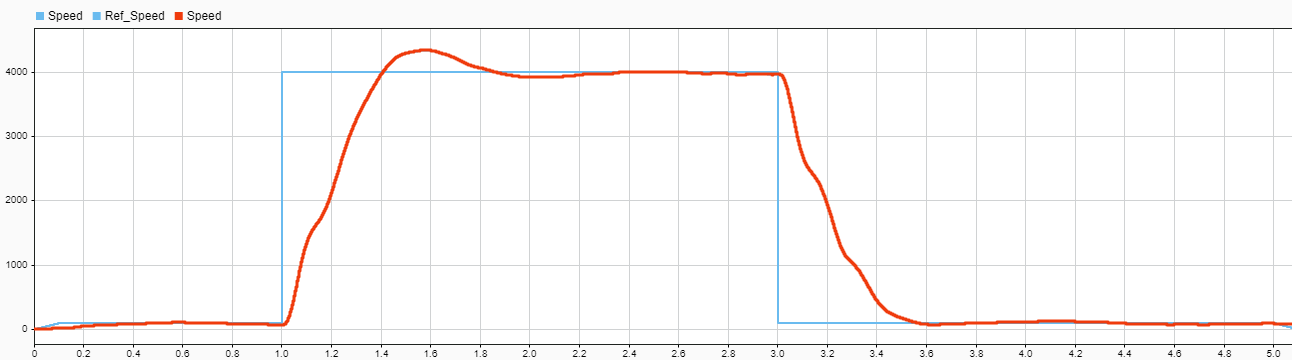
Тестируем алгоритм ADRC

С некоторых пор в Simulink появился блок управления по алгоритму Active Disturbance Rejection Control (ADRC). Чудодейственные свойства этого алгоритма давно будоражат умы разработчиков. Помнится  как TI строила  маркетинг своих библиотек под DSP говоря о превосходстве собственных закрытых реализаций ADRC. Но теперь ADRC открыт, почти полностью.

Заменим PID в нашей модели на ADRC. ADRC не имеет тюнера. Control System Tuner с ним тоже не работает, поскольку в нем нет регулируемых параметров. Коэффициенты в блоке ADRC приходится подбирать вручную. Но ADRC характеризуется тем что в нем меньше регулируемых коэффициентов и тем самым его проще настраивать чем PID.

После десятков итераций получаем такой график

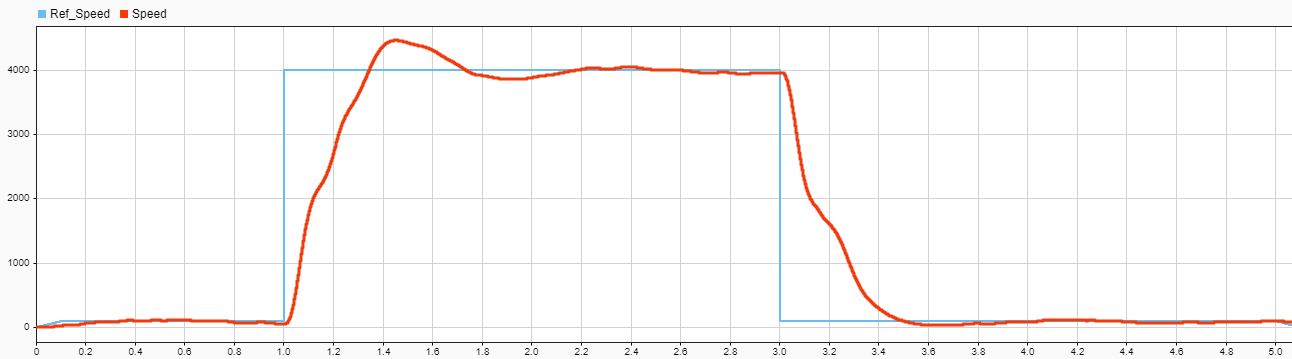
Практически тот же результат что и с PID. Т.е. пока нет оснований говорить о превосходстве ADRC.

Тестирование ADRC на детализированных моделях управления скоростью вращения ротора.

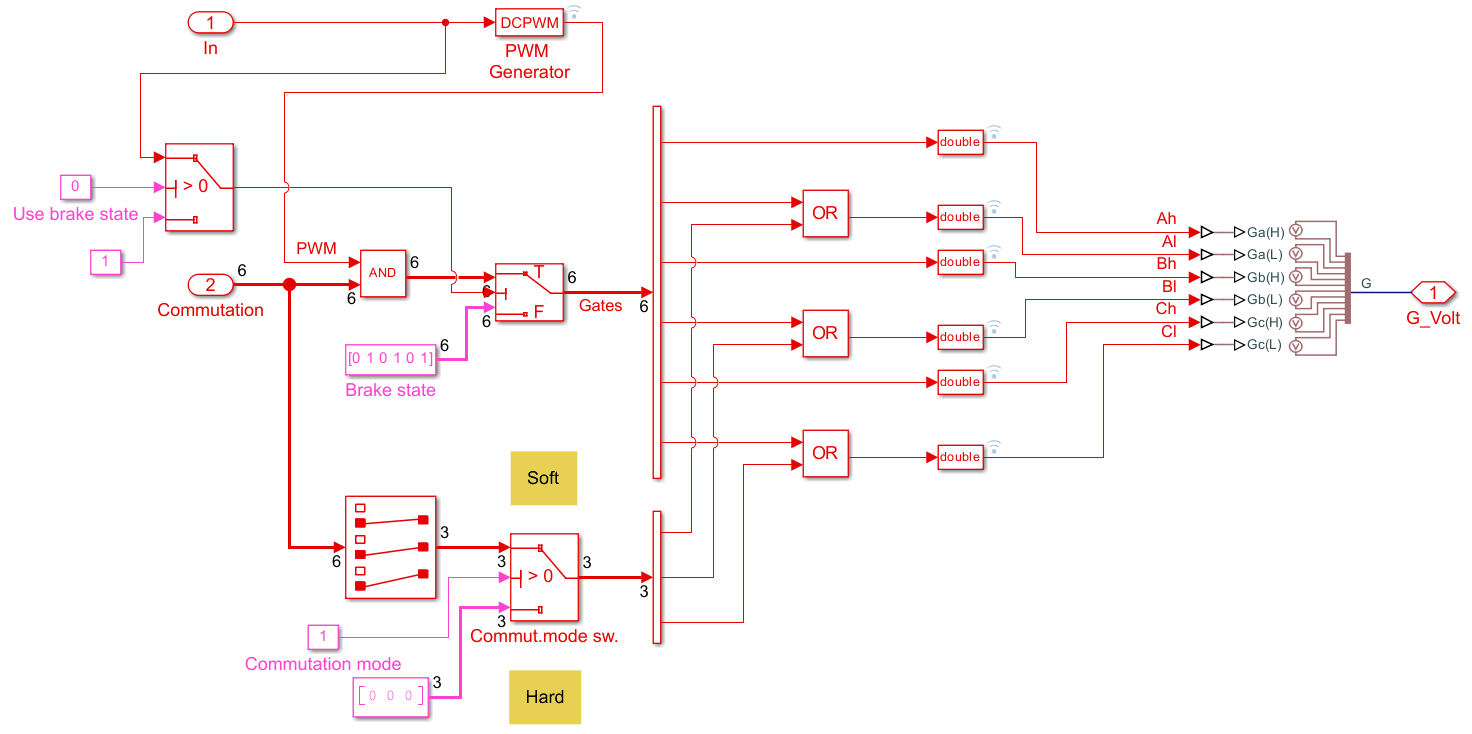
После настройки регуляторов в концептуальных моделях переходим к проверке на детализированных моделях. По сравнению с ранними моделями здесь в модуляторе были введены опции переключения режима коммутации с мягкой на жёсткую и выбор использования торможения обмотками при нулевой модуляции.

Модулятор ШИМ выдающий на выход напряжения затворов силовых транзисторов теперь выглядит так:

Модель с PID алгоритмом выглядит так:

Отклик модели  на воздействие выглядит так:

Модель с ADRC алгоритмом выглядит так:

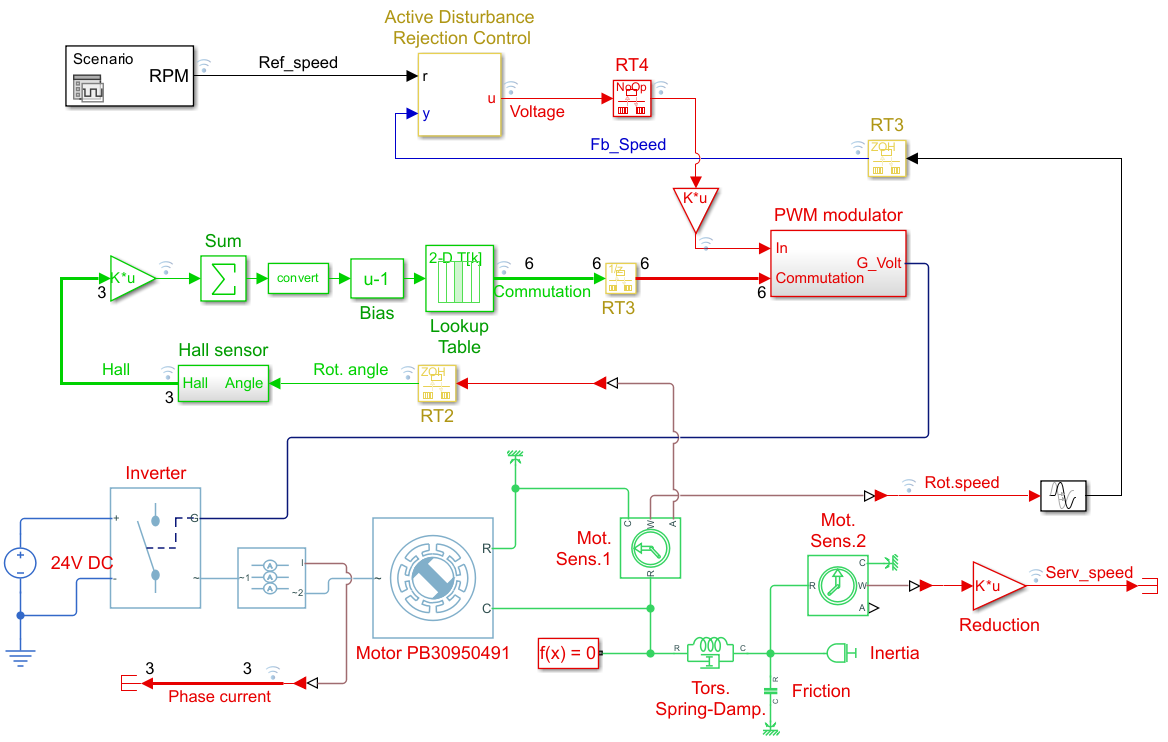
Отклик модели на воздействие выглядит так:

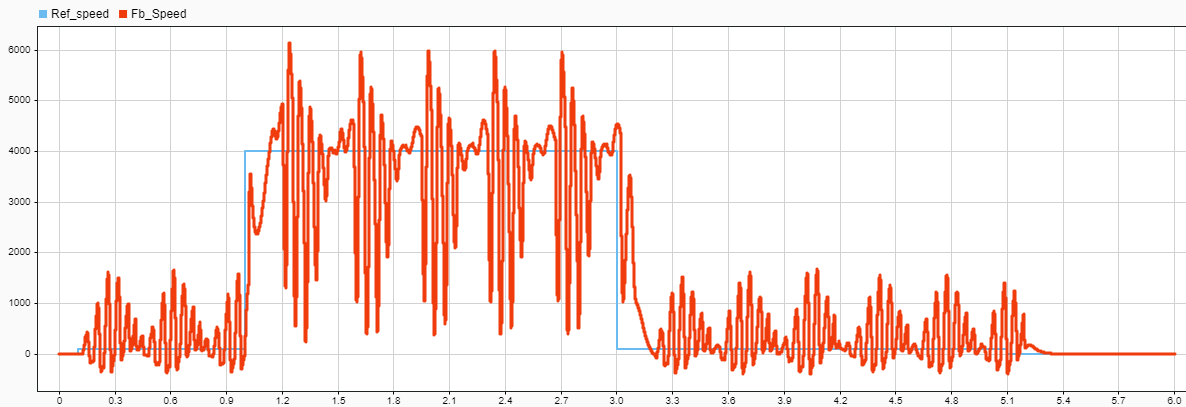
Здесь ADRC показывает худшую робастность по сравнению с PID. 

Чтобы добиться от ADRC характеристику приблизительно соответствующую референтному сигналу, как показано ниже, пришлось увеличить параметр Critical gain на два порядка!

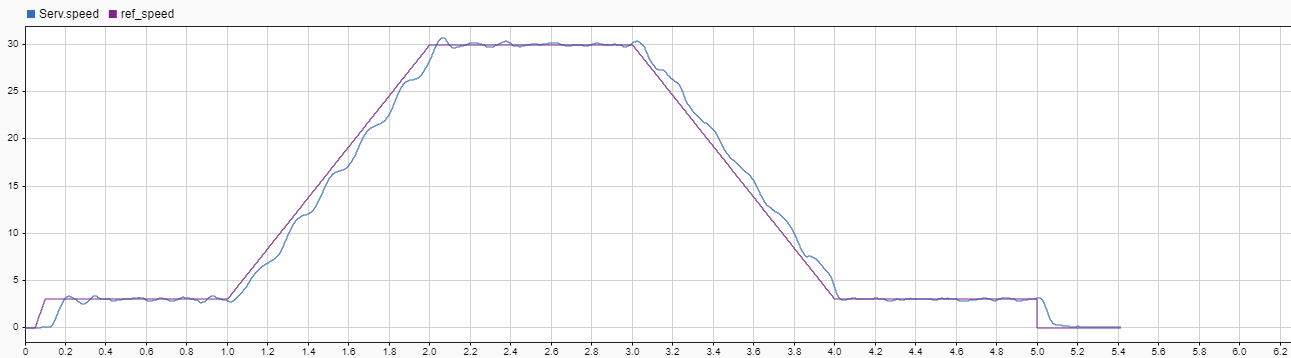
Дополнительно проводим тестирование ADRC на реальном сервоконтроллере. 

Управление скоростью с помощью ADRC в реальном устройстве.

Двухконтурный вариант раздельного управления током и скоростью с помощью ADRC не удался. Т.е.  не удалось подобрать приемлемые параметры. Но одноконтурный вариант показал приемлемые варианты как на модели так и на стенде. 

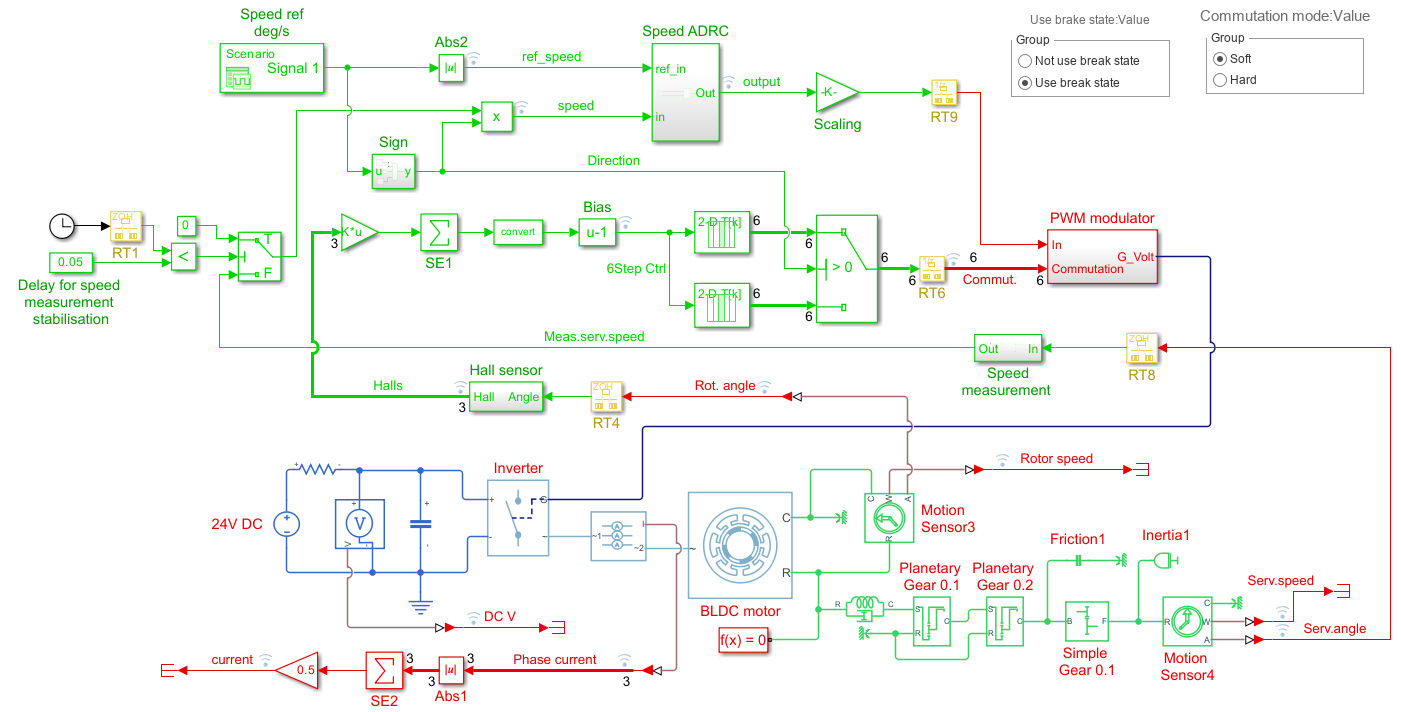
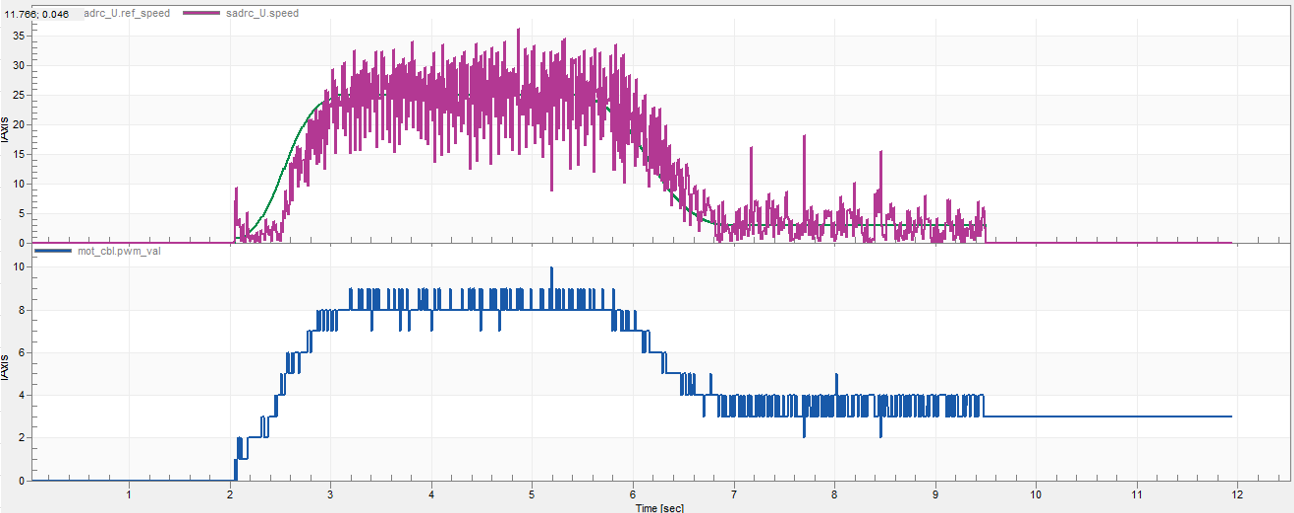
Алгоритм ADRC вычислительно сложнее PID примерно на порядок. Т.е. вместо 2-3 умножений требует 20-30 умножений. 

В Simulink компонент ADRC не даёт возможности менять параметры на ходу в реальном времени. Т.е. нельзя из него сгенерировать исходники в которых бы явно  присутствовали  параметры  Critical gain, Controller Bandwidth, Observer bandwidth и границы  выходного сигнала. Это усложняет настройку ADRC в реальном устройстве. Но мной были отрефакторены исходники ADRC и в них была реализована регулировка упомянутых параметров в реальном времени за исключением Observer bandwidth. 

Исходный текст алгоритма выглядит так:

#include "mw_cmsis.h"
#include "rtwtypes.h"

typedef struct
{
  real32_T UnitDelay_DSTATE[3];
}
DW_sadrc_T;

typedef struct
{
  real32_T Gain2_Gain[9];
}
ConstP_sadrc_T;

typedef struct
{
  real32_T ref_speed;
  real32_T speed;
}
ExtU_sadrc_T;

typedef struct
{
  real32_T u;
}
ExtY_sadrc_T;

typedef struct
{
    float f1;
    float f2;
    float k1;
    float k2;
    float k3;
    float out_lo_lim;

} T_ADRC_pars;

DW_sadrc_T     sadrc_DW; // Временные переменные 
ExtU_sadrc_T   sadrc_U;  // Вход регулятора 
ExtY_sadrc_T   sadrc_Y;  // Выход регулятора 
T_ADRC_pars    adrcp;    // Параметры регулятора  

/*-----------------------------------------------------------------------------------------------------
  ADRC step 
  Функция вызывается с частотой генерации ШИМ из оработчика прерываний АЦП

  Перед вызовом этой функции регулятор должен быть сконфигурирован функцией
  sadrc_config(float contr_bw, float b0, float out_lo_lim)

  где:
  contr_bw   - ширина полосы пропуксания регулятора ARDC в рад/сек
  b0         - Critical gain
  out_lo_lim - Ограничение минимального значения на выходе регулятора 

  В данном случае параметр Observer bandwidth фиксированный и равен 10000
-----------------------------------------------------------------------------------------------------*/
void sadrc_step(void)
{
  int32_T i;
  real32_T rtb_Gain3[3];
  real32_T tmp[3];
  real32_T tmp_0[3];
  real32_T UnitDelay_DSTATE;
  real32_T rtb_Saturation;
  real32_T rtb_Subtract;
  rtb_Subtract = sadrc_U.speed -(((0.0F * sadrc_DW.UnitDelay_DSTATE[1])+ sadrc_DW.UnitDelay_DSTATE[0])+(0.0F * sadrc_DW.UnitDelay_DSTATE[2]));
  tmp[0] = 0.846645057F * rtb_Subtract;
  tmp[1] = 7958.13F * rtb_Subtract;
  tmp[2] = 2.5696036E+7F * rtb_Subtract;
  mw_arm_add_f32(&tmp[0],&sadrc_DW.UnitDelay_DSTATE[0],&rtb_Gain3[0], 3U);
  rtb_Saturation =((((sadrc_U.ref_speed - rtb_Gain3[0]) * adrcp.f1)-(adrcp.f2 * rtb_Gain3[1])) - rtb_Gain3[2]) * adrcp.k1;
  if (rtb_Saturation > 100.0F)
  {
    rtb_Saturation = 100.0F;
  }
  else if (rtb_Saturation < adrcp.out_lo_lim)
  {
    rtb_Saturation = adrcp.out_lo_lim;
  }

  sadrc_Y.u = rtb_Saturation;
  tmp[0] = adrcp.k2 * rtb_Saturation;
  tmp_0[0] = 1.3942157F * rtb_Subtract;
  tmp[1] = adrcp.k3 * rtb_Saturation;
  tmp_0[1] = 9564.13184F * rtb_Subtract;
  tmp[2] = 0.0F * rtb_Saturation;
  tmp_0[2] = 2.5696036E+7F * rtb_Subtract;
  mw_arm_add_f32(&tmp[0],&tmp_0[0],&rtb_Gain3[0], 3U);
  rtb_Subtract = sadrc_DW.UnitDelay_DSTATE[1];
  rtb_Saturation = sadrc_DW.UnitDelay_DSTATE[0];
  UnitDelay_DSTATE = sadrc_DW.UnitDelay_DSTATE[2];
  for (i = 0; i < 3; i++)
  {
    tmp[i] =((sadrc_ConstP.Gain2_Gain[i + 3] * rtb_Subtract)+(sadrc_ConstP.Gain2_Gain[i] * rtb_Saturation))+(sadrc_ConstP.Gain2_Gain[i + 6] * UnitDelay_DSTATE);
  }
  mw_arm_add_f32(&rtb_Gain3[0],&tmp[0],&sadrc_DW.UnitDelay_DSTATE[0], 3U);
}

/*-----------------------------------------------------------------------------------------------------
  Функция конфигурирования регулятора ADRC

  \param contr_bw
  \param b0
-----------------------------------------------------------------------------------------------------*/
void sadrc_config(float contr_bw, float b0, float out_lo_lim)
{
  adrcp.f1 = contr_bw * contr_bw;
  adrcp.f2 = 2.0f * contr_bw;
  adrcp.k1 = 1.0f / b0;
  adrcp.k2 = 1.953125E-9F * b0;
  adrcp.k3 = 6.25E-5F * b0;
  adrcp.out_lo_lim = out_lo_lim;
}

Было замечено что уменьшение параметра Critical gain вызывает сильные всплески на выходе во время появления изломов на референтном сигнале. А увеличение параметра Critical gain приводит к запаздыванию реакции на изменение референтного сигнала. Т.е. реакция обратная тому что делает коэффициент при интегральной составляющей PID.   

Увеличение параметра Controller Bandwidth приводит к более высокочастотным осцилляциям на выходе ADRC. При неправильных параметрах ADRC осцилляции также легко возникают, как и при использовании PID.  

Сервопривод с алгоритмом ADRC показал хорошие результаты с первоначально нагрузкой с моментом инерции 0.15 kg*m^2, но при увеличении момента в 20 раз хорошего результата добиться не удалось:

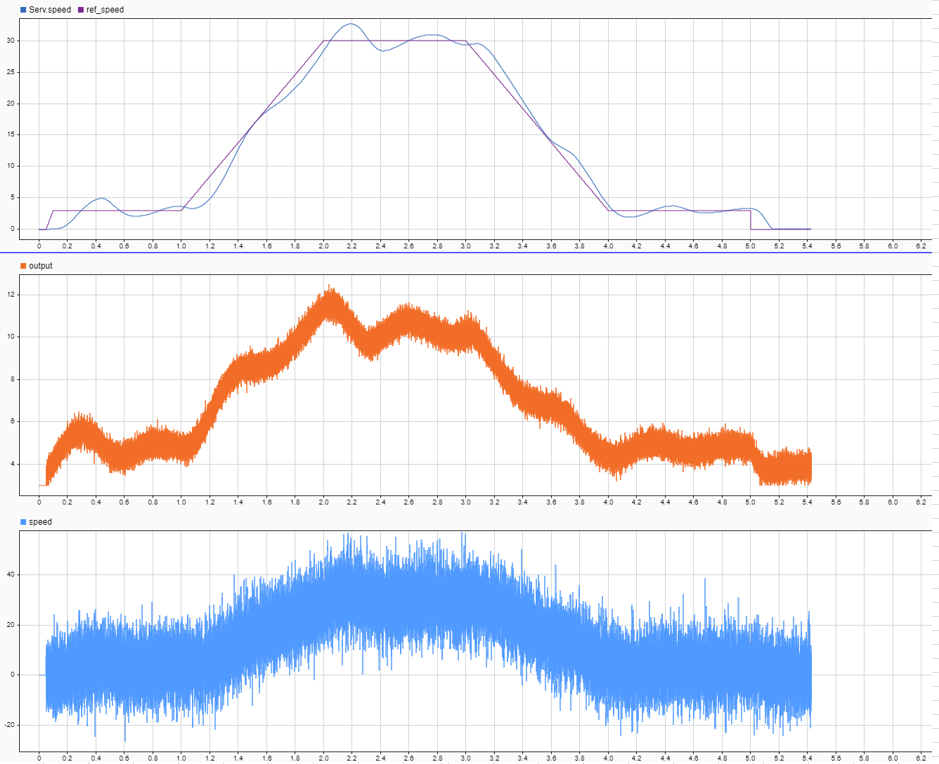
Методика расчёта параметра Critical gain предлагаемая в MATLAB не оправдалась.  Этот параметр при настройке приходится менять на порядки, т.е.  в значительно более широком диапазоне чем, например, интегральную составляющую в PID. 

Выводы

В нашем сервоприводе применен микроконтроллер с достаточно скромными ресурсами (ARM Cortex-M4, 120 МГц), поэтому в поиске алгоритмов управления мы вынуждены искать наименее вычислительно сложные решения. Хорошие кандидаты для этого - PID и ADRC. Наука еще знает LQR регуляторы, MPC регуляторы, регуляторы на основе Fuzzy logic, регуляторы на основе обучения с подкреплением Reinforcement Learning, регуляторы Model Reference Adaptive Control и прочие. Но их ресурсоемкость на embedded платформы нами пока не оценена. Поэтому работа продолжается...