... но медленный в Java, Perl, PHP, Python, Ruby, ...

Содержание

• Введение

• Регулярные выражения

• Конечный автомат

• Конвертирование регулярных выражений в НКА

• Алгоритмы поиска по регулярным выражениям

• Реализация

  • Реализация: Компиляция в НКА

  • Реализация: Симуляция НКА

• Производительность

• Кеширование НКА для построения ДКА

• Регулярные Выражения в реальности

• История и ссылки

• Заключение

• Благодарности

• Список источников

---

Введение

Речь пойдёт о двух подходах в поиске с помощью регулярных выражений (далее просто р.в.). Один из них является широко распространённым в стандартных интерпретаторах для многих языков, включая Perl. Другой используется лишь в нескольких местах, заметными из которых являются реализации в awk и grep. У этих подходов имеются значительно отличные друг друга характеристики производительности.

Ниже приведены графики времени сопоставления со строкой .

Давайте использовать следующую нотацию для повторения строк, в которой является сокращением для . На обоих графиках отражено время, требуемое каждым из подходов, для поиска по регулярному выражению в строке .

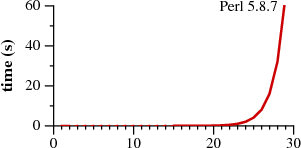
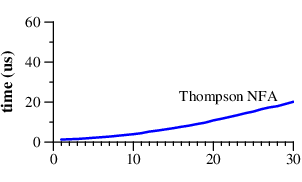
Отметим, что Perl требует более 60 секунд для того, чтобы сопоставить 29-символьную строку. Другой подход, обозначенный как "Недетерминированный Конечный Автомат (НКА) Томпсона" по причинам, которые будут объяснены позже, требует 20 микросекунд для сопоставления строки. И это не опечатка. В графике для Perl время откладывается в секундах, а в графике для НКА Томпсона - в микросекундах: НКА Томпсона в миллион раз быстрее, чем Perl реализация, запущенная на крошечной 29-символьной строке. Эта тенденция прослеживается и на продолжении графика: НКА Томпсона справляется с 200-символьной строкой менее, чем за 200 микросекунд, в то время, как Perl'у понадобилось бы более 1015 лет. (Perl - это только наиболее заметный пример большого числа популярных программ, которые используют тот же алгоритм; на графике выше мог быть и Python или PHP, или Ruby, или многие любые другие языки. Более детальный график, приведённый в статье далее, отображает данных для других реализаций.)

Может быть трудно поверить графикам: возможно вы использовали Perl и никогда не было похоже на то, что поиск по регулярным выражениям чрезвычайно медленный. По факту, большую часть времени поиск по р.в. в Perl достаточно быстрый. Однако, как показывает график, в Perl возможно писать т.н. "патологические" р.в., сопоставление по которым происходит очень-очень медленно. В отличие от этого, для реализации НКА Томпсона нет р.в., которые являлись бы патологическими. При совместном рассмотрении графиков возникает вопрос: почему Perl не использует подход с НКА Томпсона? А ведь может, и ему бы следовало это делать, и именно об этом пойдёт речь в последующей части статьи.

Исторически р.в. являются одним из блестящих примеров того, как использование хорошей теории приводит к хорошим программам. Р.в. изначально разрабатывались теоретиками просто в качестве вычислительной модели, но Кен Томпсон (Ken Thompson) представил их программистам в виде собственной реализации в текстовом редакторе QED для ОС CTSS. Денис Ритчи (Dennis Ritchie) последовал примеру в своей собственной реализации QED для GE-TSS. Томпсон и Ритчи продолжили создавать Unix, и взяли р.в. с собой. К поздним 70ым, р.в. были ключевой возможностью в ландшафте Unix, в таких инструментах, как ed, grep, egrep, awk и lex.

В наши дни р.в. являются таким же блестящим примером того, как игнорирование хорошей теории ведёт к плохим программам. Реализации р.в., используемые в сегодняшних популярных инструментах, значительно медленнее тех, что использовались во множестве инструментах Unix тридцатилетней давности.

В этой статье так же приводится обзор хорошей теории: регулярные выражения, конечные автоматы и алгоритм поиска по р.в., изобретённый Кеном Томпсоном в середине 60х. Также обращаем теорию в практику, описывая простую реализацию алгоритма Томпсона. Эта реализация, менее чем в 400 строк кода на Си, бежит голова к голове с реализацией Perl. Она обгоняет более сложные реализации из реального мира, используемые Perl'ом, Python'ом, PCRE и прочими. Статья завершается обсуждением того, как теория ещё может быть применена на практике в реализациях в реальном мире.

Регулярные выражения

Регулярные выражения - это описательная нотация для множеств символьных строк. Когда конкретная строка подпадает под множество строк, описанных р.в., мы часто говорим, что строка совпадает (сопоставляется) с р.в.

Простейшее р.в. - это одиночный литеральный символ. За исключением специальных метасимволов , , , , , , символы совпадают с сами собой. Чтобы сопоставить метасимвол, его необходимо экранировать обратной косой чертой (backslash): совпадает с символом "плюс".

Два регулярных выражения могут быть соединены через логическое И (конкатенация) или через логическое ИЛИ (операция альтернативы, операция выбора) в виде нового регулярного выражения: если совпадает с s, а совпадает с t, тогда совпадает с s или с t, а совпадает с st.

Метасимволы , и являются операторами повторений: совпадает с последовательностью из нуля или более строк, каждая из которых совпадает с ; совпадает с одной или более строками; совпадает с нулём или одной строками.

Приоритет операторов, от менее приоритетному к более приоритетному: сначала альтернатива, потом конкатенация, и в конце операторы повторения. Явные скобки могут использоваться для принудительного изменения порядка, как в арифметических выражениях. Немного примеров: является эквивалентом ; а - .

Описанный синтаксис является подмножеством синтаксиса р.в. в традиционной Unix утилите egrep. Это подмножество является достаточным для того, чтобы описать все регулярные языки. Грубо говоря, регулярный язык - это множество строк, которое может быть сопоставлено за один проход через текст, используя только фиксированный объём памяти. Более новые движки регулярных выражений (отметим Perl и тех, кто копирует его) добавили множество новых операторов и экранирующих последовательностей. Эти добавления сделали р.в. более короткими и иногда более трудно читаемыми, но обычно не более функциональными: эти продвинутые новые р.в. почти всегда имеют более длинный эквивалент в традиционном синтаксисе.

Одно распространённое расширение р.в., которое расширяет их возможности, называется обратными ссылками (backreferences). Обратные ссылки, такие как или совпадают со строками, которые сопоставились с предыдущим выражением в скобках, и только с ним: совпадает с catcat и dogdog, но не с catdog или dogcat. Что же касается теоретической терминологии, то р.в. с обратными ссылками не являются р.в. За возможности, которые добавляются обратными ссылками, приходится дорого платить: в худшем случае в наиболее известных реализациях это требует поисковых алгоритмов с экспоненциальной сложностью, подобных тем, что используются в Perl. Perl (и другие языки) не могут уже удалить поддержку обратных ссылок, конечно же, но могут использовать более быстрые алгоритмы, когда в р.в., подобных представленному выше, нет обратных ссылок. Эта статья как раз об этих более быстрых алгоритмах.

Конечный автомат

Другим способом описать множество символьных строк является применение конечных автоматов. Конечный автомат (finite automata), так же известный как машина состояний (state machine), и мы будем использовать термины "автомат" и "машина", как взаимозаменяемые. (Прим: в русскоязычной терминологии словосочетание "машина состояний" редко используется, поэтому далее будет использоваться слово "автомат", а так же сокращения "ДКА" (детерминированный конечный автомат, англ. DFA) и "НКА" (недетерминированный конечный автомат, англ. NFA))

В качестве простого примера, здесь представлен автомат, распознающий множество строк, которые описываются р.в. .

Конечный автомат всегда находится в одном из своих состояний, изображённых на диаграмме окружностями. (Число внутри окружности - это метки, чтобы сделать обсуждение проще; они не являются частью процесса функционирования автомата.) По мере чтения строки происходят переходы из состояния в состояние. У этого автомата два особых состояния: начальное состояние (start state) , и состояние совпадения (match state) . На начальные состояния указывают одиночные стрелки (ведущие из ниоткуда), а состояния совпадения изображаются двойными окружностями.

Автомат читает входную строку по символу за раз. Соответствующие входным данным стрелки представляют собой переходы из состояния в состояние. Допустим, входной строкой является abbbba. Когда автомат читает первую букву строки (a), он находится в начальном состоянии . Он следует по стрелке и переходит в состояние . Этот процесс повторяется, пока автомат читает остаток строки: читая символ b он переходит в состояние , b - , ещё одну b - возвращается в , потом по b снова в , и наконец-таки читая a переходит в .

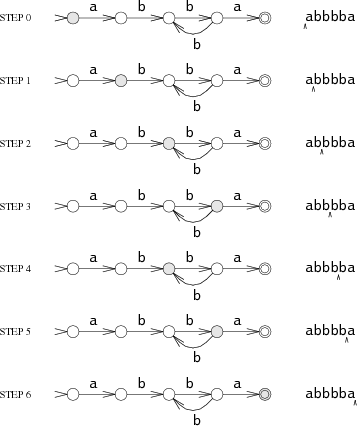
Автомат заканчивает работу в состоянии , состоянии совпадения, и таким образом он сопоставляет (распознаёт) строку. Если автомат заканчивает работу не в состоянии совпадения, то он не сопоставляет (не распознаёт) строку. Если в любой момент работы автомата нет перехода, соответствующего текущему входному символу, автомат преждевременно завершает свою работу.

Автомат, который мы только что рассмотрели, называется детерминированным конечным автоматом (ДКА, англ. Deterministic Finite Automata, DFA), потому что для любого состояния каждый входящий символ ведёт не более, чем в одно другое состояние. Например, этот автомат является эквивалентом предыдущего, но уже не является детерминированным:

Автомат не является детерминированным, потому что если он читает b, находясь в состоянии , у него есть несколько вариантов для выбора следующего состояния: он может вернуться в в надежде встретить другую последовательность bb, или может перейти в в надежде встретить завершающее a. Так как автомат не может заглянуть вперёд, чтобы подглядеть остаток строки, у него нет возможности узнать, какое из решений является верным. В этой ситуации оказывается интересным позволить автомату всегда правильно угадывать. Такие автоматы называются недетерминированными конечными автоматами (НКА, НДКА, NFA или NDFA). НКА распознаёт входящую строку, если существует какой-либо способ прочитать её и перейти в состояние совпадения.

Иногда бывает удобно позволить НКА иметь переходы без соответствующего входного символа. Мы оставляем такие стрелки без меток (прим: в теории автоматов такие переходы называются эпсилон-переходами и обозначаются соответствующей буквой ). НКА в любой момент может решить проследовать по стрелке без символа, при этом не читая символ из входной строки. Этот НКА эквивалентен двум предыдущим, но стрелка без метки делает соответствие выражению более явным:

Конвертирование Регулярных Выражений в НКА

Регулярные выражения и НКА по возможностям совершенно эквивалентны: у каждого р.в. есть эквивалентный НКА (они сопоставляют одни и те же строки) и наоборот. (Так же ДКА эквивалентны НКА и р.в. по возможностям; это будет видно позднее.) Есть множество способов преобразовать р.в. в НКА. Описанный здесь метод впервые был представлен в работе Томпсона в 1968.

НКА для р.в. строится из частей НКА, которые соотвествуют каждому подвыражению, и комбинируются различным образом, в зависимости от каждого оператора. Части НКА не имеют состояний совпадения: вместо этого у них есть одна или более стрелок, указывающих в никуда. Процесс конструирования завершается этапом присоединения этих стрелок к состоянию совпадения.

НКА для сопоставления одиночного символа выглядят так:

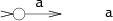
НКА для конкатенированного выражения соединяет конечное состояние автомата и начальное состояние автомата :

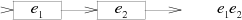
НКА для выражения с альтернативой добавляет новое начальное состояние, в котором происходит выбор либо автомата , либо автомата :

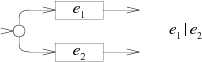
НКА для выражения изменяет автомат, добавляя пустой путь (т.н. -переход):

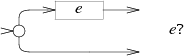
НКА для выражения использует то же самое преобразование, но замыкает автомат на начальное состояние самого себя:

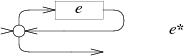
НКА для выражения так же создаёт петлю, но требует перехода через не менее одного раза:

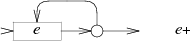
Подсчитывая новые состояния в диаграммах, мы можем заметить, что при этой технике создаётся ровно одно состояние на один символ или метасимвол в р.в., за исключением скобок. Следовательно, количество состояний в финальном НКА будет равно самое большее длине оригинального р.в.

Как и в примере с обсуждаемым выше НКА, всегда можно удалить стрелки без меток и всегда возможно сгенерировать НКА сразу без них. НКА с неподписанными стрелками проще для чтения и понимания, а также проще в представлении в виде кода на Си, так что мы эти стрелки оставим.

Алгоритмы поиска по регулярным Выражениям

Теперь у нас есть способ проверить сопоставление р.в. и строки: сконвертировать р.в. в НКА и затем запустить его, используя строку в качестве входных данных. Помните, что НКА обладают способностью идеально угадывать следующее состояние, когда встают перед выбором: выполняя НКА на обычном компьютере, мы должны найти способ симулировать это угадывание.

Один из способов симуляции идеального угадывания заключается в выборе одного из вариантов, и если он не подойдёт, то попробовать другой. Для примера возьмём НКА для выражения на строке abbb:

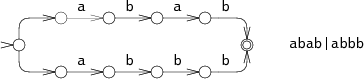
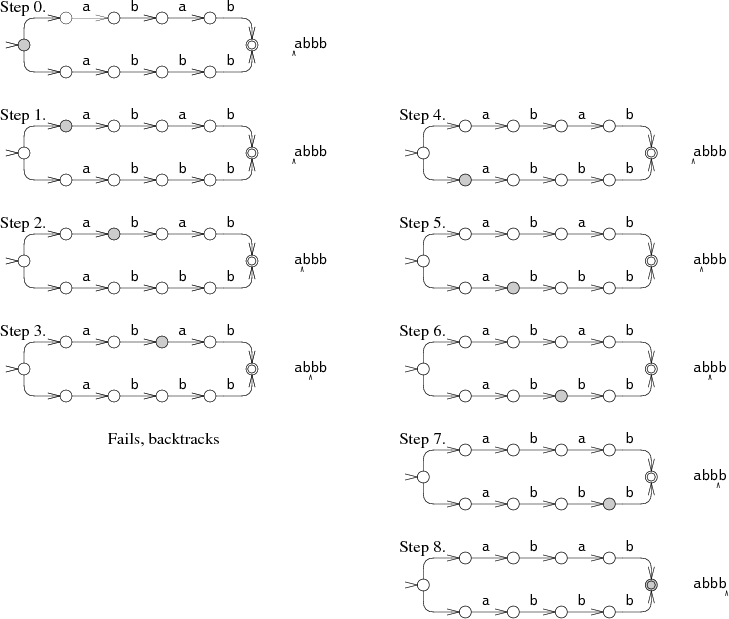
На шаге 0 НКА должен принять решение: попытаться проверить abab или abbb. На диаграмме показано, как НКА пытается проверить abab, но терпит неудачу после шага 3. Затем НКА пытается проверить другой выбор, приводящий его к шагу 4 и, естественно, к совпадению. Этот подход с возвратом (aka алгоритм с возвратом, backtracking) имеет простую рекурсивную реализацию, но может приводить к многократному чтению входной строки перед тем, как вернуть совпадение. Если строка не соответствует р.в., автомат должен перепробовать все возможные пути выполнения перед тем, как сдаться. В данном примере НКА проверяет только два разных пути, но в самом худшем случае возможно экспоненциальное множество возможных путей выполнения, что приводит к очень медленной работе.

Более эффективный, но более сложный способ симуляции идеального угадывания - пробовать оба варианта одновременно. При этом подходе симуляция позволяет автомату находиться сразу в нескольких состояниях. Обрабатывая каждый входной символ, автомат переходит по соответствующим стрелкам из каждого состояния.

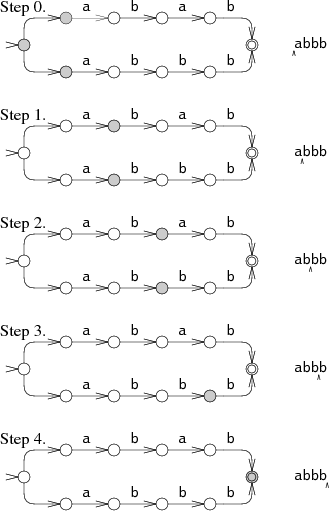
Автомат начинает со стартового состояния и всех состояний, доступных из него по немаркированным стрелкам. На шагах 1 и 2 НКА находится в двух состояниях одновременно. И только на шаге 3 количество его состояний сокращается до одного. При этом мультистейтном (multi-state, суперпозиционном) подходе проверяются оба пути в одно и то же время, читая входные данные лишь один раз. В самом худшем случае НКА может находиться во всех возможных состояниях сразу на каждом шаге, но это приводит лишь к константному объёму вычислений без зависимости от длины входной строки. И таким образом, входные строки даже значительной длины могут быть обработаны за линейное время. Это гигантское улучшение относительно экспоненциального времени, которое требуется подходу с возвратом. Эффективность обусловлена отслеживанием множества доступных состояний, а не множества путей, которые используются для их достижения. В случае автомата с n узлами, на каждом шаге есть только n доступных состояний, но при этом может существовать путей между узлами.

Реализация

Томпсон представил подход с мультистейтной симуляцией в своей работе 1968 года. В его формулировке состояния НКА были представлены небольшими последовательностями машинного кода, а список возможных состояний представлял собой просто последовательность инструкций вызова функций. По сути, Томпсон компилировал р.в. в умный машинный код. Сорок лет спустя компьютеры работают во много раз быстрее, и подход с машинным кодом уже не является необходимостью. Следующие части статьи содержат реализацию, написанную на портабельном ANSI C. Полный исходный код (менее 400 строк) и скрипты для проверки производительности доступны онлайн. (Читатели, которым не знаком или кому неприятны Си и/или указатели, могут читать лишь описание и пропустить сам код.)

Реализация: Компиляция в НКА

Первым этапом является компиляция р.в. в эквивалентный НКА. В нашей программе на Си мы будет представлять НКА в виде связанной коллекции структур типа State:

struct State
{
    int c;
    State *out;
    State *out1;
    int lastlist;
};

Каждая структура State представляет собой один из трёх фрагментов НКА, в зависимости от значения поля c.

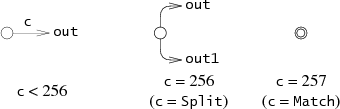
Согласно работе Томпсона, компилятор строит НКА из р.в., представленного в постфиксной записи, с добавлением оператора . (точка), являющемся явным оператором конкатенации (соединения по И). Отдельная функция re2post переписывает р.в. в инфиксной нотации (например, ) в эквивалентное р.в. в постфиксной нотации () ("Настоящей" реализации понадобилось бы использовать оператор . в качестве метасимвола "любой символ", а не в качестве оператора соединения. Так же настоящие реализации возможно строили бы НКА в процессе разбора р.в. вместо построения выражения в постфиксной нотации. Однако, постфиксная версия удобнее и идеологически ближе к работе Томпсона.)

По мере сканирования постфиксного выражения, компилятор управляет стеком вычисленных фрагментов НКА. Литералы вталкивают новые фрагменты НКА на вершину стека, а операторы сначала выталкивают фрагменты из стека, а затем вталкивают новый фрагмент. Например, после компиляции из выражения , стек содержит фрагменты НКА для литералов , и . Компиляция приводит к выталкиванию двух фрагментов из стека, и заталкивает в стек выражение конкатенации . Каждый фрагмент НКА определён своим стартовым состоянием и исходящими из него переходами:

struct Frag
{
    State *start;
    Ptrlist *out;
};

Поле start указывает на начальное состояние для фрагмента, а поле out - список указателей на указатели State, которые ещё ни к чему не подключены. Это "висячие" переходы во фрагменте НКА.

union Ptrlist
{
	Ptrlist *next;
	State *s;
};

Кое-какие вспомогательные функции для управления списками указателей:

Ptrlist *list1(State **outp);
Ptrlist *append(Ptrlist *l1, Ptrlist *l2);

void patch(Ptrlist *l, State *s);

Функция list1() создаёт новый список указателей, состоящий из одиночного указателя outp. Функция append() соединяет два списка указателей, возвращая результат. Функция patch присоединяет "висячий" переход в списке указателей l к состоянию s: выполняет присваивание *outp = s для каждого указателя outp в списке l.

Получив эти примитивы и фрагмент стека, компилятор просто проходит в цикле по постфиксному выражению. В результате остаётся одиночный фрагмент, присоединив к которому состояние совпадения, мы получаем завершённый НКА.

State*
post2nfa(char *postfix)
{
    char *p;
    Frag stack[1000], *stackp, e1, e2, e;
    State *s;

    #define push(s) *stackp++ = s
    #define pop()   *--stackp

    stackp = stack;
    for(p=postfix; *p; p++){
        switch(*p){
        /* различные случаи, описанные далее */
        }
    }
    
    e = pop();
    patch(e.out, matchstate);
    return e.start;
}

Специфические случаи компиляции:

Литеральные символы:

default:
    s = state(*p, NULL, NULL);
    push(frag(s, list1(&s->out));
    break;

Соединение по И (конкатенация):

case '.':
    e2 = pop();
    e1 = pop();
    patch(e1.out, e2.start);
    push(frag(e1.start, e2.out));
    break;

Соединение по ИЛИ (альтернатива):

case '|':
    e2 = pop();
    e1 = pop();
    s = state(Split, e1.start, e2.start);
    push(frag(s, append(e1.out, e2.out)));
    break;

Нуль или один:

case '?':
    e = pop();
    s = state(Split, e.start, NULL);
    push(frag(s, append(e.out, list1(&s->out1))));
    break;

Нуль и более:

case '*':
    e = pop();
    s = state(Split, e.start, NULL);
    patch(e.out, s);
    push(frag(s, list1(&s->out1)));
    break;

Один и более:

case '+':
    e = pop();
    s = state(Split, e.start, NULL);
    patch(e.out, s);
    push(frag(e.start, list1(&s->out1)));
    break;

Реализация: Симуляция НКА

Теперь, после того как НКА сформирован, нужно симулировать его работу. Симуляция требутет отслеживания множества структур State, которые хранятся в виде простого массива:

struct List
{
    State **s;
    int n;
};

Симуляция использует два списка: clist - множество состояний, в которых НКА находится в данный момент, и nlist - множество состояний, в которых НКА окажется после обработки текущего символа. Цикл работы инициализирует clist, помещая в него лишь начальное состояние, а потом запускает автомат в пошаговом режиме.

int
match(State *start, char *s)
{
    List *clist, *nlist, *t;

    /* l1 and l2 are preallocated globals */
    clist = startlist(start, &l1);
    nlist = &l2;
    for(; *s; s++){
        step(clist, *s, nlist);
        t = clist; clist = nlist; nlist = t;    /* swap clist, nlist */
    }
    return ismatch(clist);
}

Чтобы избежать выделения памяти на каждой итерации цикла, функция match использует два преаллоцированных списка l1 и l2 в качестве clist и nlist, обменивая их содержимое после каждого шага.

Если список конечных состояний содержит состояния совпадения, значит строка подпадает под р.в.

int
ismatch(List *l)
{
    int i;

    for(i=0; i<l->n; i++)
        if(l->s[i] == matchstate)
            return 1;
    return 0;
}

Функция addstate добавляет состояние в список, но только если его там ещё нет. Полное сканирование списка для каждого добавления было бы неэффективным. Вместо этого переменная listid выступает в качестве номера поколения списка (list generation number). Когда addstate добавляет s в список, в s->lastlist записывается значение listid. Если при этом эти два значения равны, тогда s уже находится в списке. Функция addstate так же проходит по немаркированным стрелкам: если s является состоянием Split с двумя немаркированными стрелками, ведущими в новые состояния, addstate добавляет эти состояния в список вместо состояния s.

void
addstate(List *l, State *s)
{
    if(s == NULL || s->lastlist == listid)
        return;
    s->lastlist = listid;
    if(s->c == Split){
        /* follow unlabeled arrows */
        addstate(l, s->out);
        addstate(l, s->out1);
        return;
    }
    l->s[l->n++] = s;
}

Функция startlist создаёт список начальных состояний, просто добавляя в него стартовое состояние:

List*
startlist(State *s, List *l)
{
    listid++;
    l->n = 0;
    addstate(l, s);
    return l;
}

И наконец, функция step прогоняет одиночный символ через НКА, используя список текущих состояний clist для вычисления списка следующих состояний nlist:

void
step(List *clist, int c, List *nlist)
{
    int i;
    State *s;

    listid++;
    nlist->n = 0;
    for(i=0; i<clist->n; i++){
        s = clist->s[i];
        if(s->c == c)
            addstate(nlist, s->out);
    }
}

Производительность

Представленная реализация на Си не была написана с прицелом на производительность. Но даже так, медленная реализация алгоритма с линейной сложностью по времени может легко обогнать быструю реализацию алгоритма с экспоненциальной сложностью, когда экспонента достаточно велика. Это демонстрируется при тестировании различных популярных движков р.в. на т.н. патологическом регулярном выражении.

Дано р.в. . Оно сопоставляет строку , когда не забирает никаких символов для совпадения, оставляя всю строку целиком только под совпадение с . Движки р.в. с возвратом (бектрекингом) реализуют (нуль-или-одно), сначала проверяя единичное вхождение, а затем отсутствие вхождения символа. Если есть таких вариантов, для которых надо принять решение, то всего будет возможных вариантов решений. Но только последний вариант, когда для всех операторов (т.н. квантификаторов) выбрано нуль вхождений, происходит совпадение строки. Таким образом, подход с бектрекингом требует времени, и не масштабируется при и более.

В отличие от этого, алгоритм Томпсона управляет списками состояний длиной примерно и обрабатывает строку так же длиной , что в результате даёт сложность по времени в . (Время работы линейно, потому что мы не сохраняем р.в. константным по мере роста входной строки. Для р.в. длиной на строке длиной НКА Томпсона требует времени.)

Следующий график отображает время, которое требуется для проверки строки с помощью р.в. :

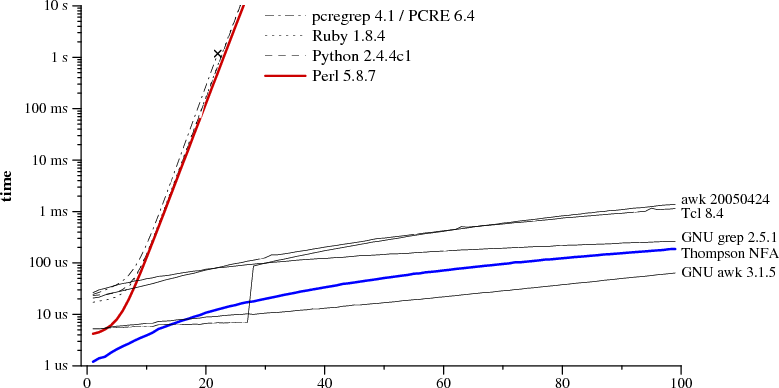
Отметим, что y-координата откладывается по логарифмической шкале для более наглядного представления различий по времени на одном графике.

Из графика ясно, что Perl, PCRE, Python и Ruby используют механизм рекурсивного бектрекинга. PCRE останавливает поиск правильного ответа на , потому что он прекращает работу после максимального количества шагов. Начиная с Perl 5.6, его движок р.в. использует запоминание (мемоизацию) рекурсивного поиска с возвратом, что должно при некоторых затратах памяти удерживать время поиска не экспоненциальным, если не используются обратные ссылки. Как показывает график, мемоизация происходит не полностью: время растёт по экспоненте даже при отсутствии обратных ссылок в выражении. Не смотря на то, что Java здесь не тестировалась, она так же использует реализацию с возвратом. По факту, интерфейс java.util.regex требует реализацию с возвратом, поскольку при выполнении поиска можно выполнять произвольный код. PHP использует библиотеку PCRE.

Тонкая голубая линия - это реализация алгоритма Томпсона на Си, данная выше. Awk, Tcl, GNU grep и GNU awk строят ДКА не предвычисляя их или используя конструирование налету, описанное в следующей части.

Можно возразить, что тест не очень справедлив к реализациям с возвратом, т.к. сфокусирован на редком случае. Этот аргумент упускает суть: если есть выбор между реализацией, которая работает с предсказуемым, постоянным и малым временем поиска на всех входных данных, и реализацией, которая обычно работает быстро, но может потребовать годы процессорного времени (или даже больше) на некоторых входных данных, то решение о выборе простое. Кроме того, хотя столь драматичные примеры вроде этого на практике встречаются редко, встречаются и менее драматичные. Примеры включают в себя р.в. для разбиения строки из пяти полей по пробелам, или использование альтернатив, когда входящая строка не указана первой. В результате программисты часто исследуют, какие из конструкций являются дорогостоящими и избегают их применения; или часто используют различные т.н. оптимизаторы. Использование НКА Томпсона не требует подобных ухищрений: для него нет дорогостоящих р.в.

Кеширование НКА для построения ДКА

Напомню, что ДКА более эффективны при исполнении, чем НКА, потому что ДКА всегда находятся только в одном из состояний в каждый момент времени: у них никогда не бывает выбора из нескольких следующих состояний. Любой НКА можно конвертировать в эквивалентный ДКА, в котором каждое из состояний соответствует списку состояний НКА.

Например, вот НКА, который использовался ранее для р.в. , в который добавлены номера состояний:

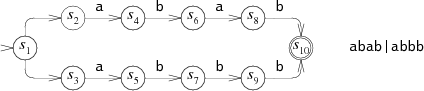
Эквивалентный ДКА мог бы выглядеть вот так:

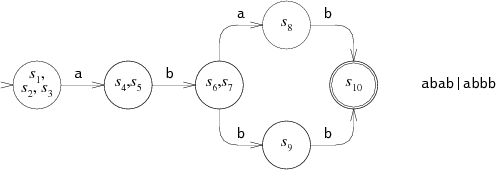
Каждое состояние в ДКА соответствует списку состояний из НКА.

В некотором роде, симуляция НКА Томпсона выполняет эквивалентный ДКА: каждый List соответствует какому-то состоянию ДКА, и функция step вычисляет, принимая list и следующий символ, в какое из следующих состояний ДКА перейти. Алгоритм Томпсона симулирует ДКА, вычисляя каждое из его состояний по мере надобности. Вместо того, чтобы отбрасывать результаты этой работы после каждого шага, мы можем закешировать значения List в свободной памяти, избежав затрат на повторение вычислений в будущем и, по сути, вычисляя эквивалентный ДКА по мере необходимости. Эта часть представляет реализацию данного подхода. Начав с реализации НКА из предыдущей части, нам нужно добавить менее ста строк для реализации ДКА.

Чтобы реализовать кеш, сперва добавим новый тип данных, который представляет собой состояние ДКА:

struct DState
{
    List l;
    DState *next[256];
    DState *left;
    DState *right;
};

Значение DState является закешированной копией списка l. Массив next содержит указатели на следующее состояние для каждого возможного входного символа: если текущее состояние d и следующий символ со входа c, тогда d->next[c] будет следующим состоянием. Если d->next[c] содержит значение null, тогда следующее состояние ещё не было вычислено. Функция nextstate вычисляет, записывает и возвращает следующее состояние для заданного состояния и символа.

Сопоставление с р.в. происходит через циклическое следование по значению в d->next[c], при необходимости выполняя функцию nextstate для вычисления следующих состояний.

int
match(DState *start, char *s)
{
    int c;
    DState *d, *next;
    
    d = start;
    for(; *s; s++){
        c = *s & 0xFF;
        if((next = d->next[c]) == NULL)
            next = nextstate(d, c);
        d = next;
    }
    return ismatch(&d->l);
}

Все значения Dstate, которые были вычислены, нужно сохранить в структуре, которая позволит нам найти их по заданному значению List. Для этого организуем их в бинарное дерево, используя сортированное значение List в качестве ключа. Функция dstate возвращает значение DState для переданного List, при необходимости выделяя память:

DState*
dstate(List *l)
{
    int i;
    DState **dp, *d;
    static DState *alldstates;

    qsort(l->s, l->n, sizeof l->s[0], ptrcmp);

    /* look in tree for existing DState */
    dp = &alldstates;
    while((d = *dp) != NULL){
        i = listcmp(l, &d->l);
        if(i < 0)
            dp = &d->left;
        else if(i > 0)
            dp = &d->right;
        else
            return d;
    }
    
    /* allocate, initialize new DState */
    d = malloc(sizeof *d + l->n*sizeof l->s[0]);
    memset(d, 0, sizeof *d);
    d->l.s = (State**)(d+1);
    memmove(d->l.s, l->s, l->n*sizeof l->s[0]);
    d->l.n = l->n;

    /* insert in tree */
    *dp = d;
    return d;
}

Функция nextate выполняет шаг НКА и возвращает соответствующее значение DState:

DState*
nextstate(DState *d, int c)
{
    step(&d->l, c, &l1);
    return d->next[c] = dstate(&l1);
}

И наконец, начальное состояние ДКА - это значение DState, соответствующее начальному списку состояний НКА:

DState*
startdstate(State *start)
{
    return dstate(startlist(start, &l1));
}

(Как и в симуляции НКА, l1 является преаллоцированным значением List.)

Значения DState соответствуют состояниями ДКА, но которые строятся только по мере необходимости: если состояние ещё не встретилось в процессе поиска, его не будет в кеше. Альтернативой могло бы быть вычисление всего ДКА за раз. Это могло бы сделать сопоставление немного быстрее за счёт удаления ветки с условием, но ценой увеличения времени запуска и расходом памяти.

Можно так же побеспокоиться об ограничении объёма памяти, используемого конструированием ДКА налету. Т.к. DStates является только кешем значений функций step, реализация dstate может отбросить ДКА целиком, если кеш вырос слишком сильно. Эта политика замены требует всего лишь несколько дополнительных строк кода в функциях dstate и nextstate, плюс около 50 строк кода для управления памятью. Такая реализация доступна онлайн. (awk использует похожую стратегию ограничения по размеру с фиксированным лимитом в 32 закешированных состояния, что объясняет его производительность после n=28 на графике выше.)

НКА, полученные из р.в., имеют склонность демонстрировать хорошую локальность: они посещают одни и те же состояния и следуют по тем же самым переходам снова и снова при запуске на большинстве текстов. Это делает кеширование целесообразным: при первом прохождении по стрелке следующее состояние необходимо вычислить, как и в симуляции НКА, но последующие переходы по этой же стрелке являются лишь единичным обращением к памяти. Реальные реализации на основе ДКА могут использовать дополнительные оптимизации для ещё более быстрого исполнения. В сопутствующей статье более подробно рассмотрены реализации р.в. на основе ДКА.

Регулярные выражения в реальности

Использование р.в. в реальных программах несколько сложнее, чем то, с чем могут справиться описанные выше реализации. В этой части кратко описаны распространённые усложнения. Полное рассмотрение каждого из них выходит за рамки данной вводной статьи.

Символьные классы (character classes). Символьный класс, не важно, [0-9] или \w или . (точка), является просто сокращённым представлением альтернативы, в которую могут быть развёрнуты во время компиляции. Хотя более эффективно добавить новый тип узла НКА для их явного представления. POSIX определяет специальные символьные классы вроде [[:upper:]], которые меняют своё значение в зависимости от текущей локали. Но сложность в их адаптации является как раз определение значения, а не представление этого значения внутри НКА.

Экранирующие последовательности (escape sequences). Синтаксис реальных р.в. требует обработки экранирующих последовательностей, как для сопоставления с метасимволами (\(, \), \\ и т.п.), так и для всяких разных трудновводимых символов вроде \n.

Считанное повторение (counted repetition). Многие реализации р.в. предоставляют оператор считанных повторений {n} для сопоставления точного количества повторений шаблона; {n,m} сопоставляет не менее n и не более m повторений, а {n,} сопоставляет n и более. Реализации с рекурсивным возвратом могут реализовать считанные повторения, используя циклы. Реализации на основе НКА или ДКА обязаны раскрывать эти повторения: e{3} раскрывается в eee; e{3,5} - в eeee?e?, а e{3,} - в eee+.

Извлечение подвыражений (подстрок) (submatch extraction). Когда р.в. используются для разбиения или разбора строк, бывает полезно иметь возможность найти подстроки, которые соответствуют каждому найденному подвыражению. После того, как р.в. вроде ([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+) сопоставило строку (скажем, дату и время), многие движки р.в. предоставляют доступ к тексту, который совпал с каждым выражением в скобках. Например, вот как это может быть написано на Perl'е:

if(/([0-9]+-[0-9]+-[0-9]+) ([0-9]+:[0-9]+)/){
    print "date: $1, time: $2\n";
}

Извлечение границ подвыражений большей частью игнорировалось теоретиками компьютерных наук, и, наверное, это самый сильный аргумент в пользу рекурсивного алгоритма с возвратом. Однако же, алгоритмы в стиле Томпсона могу быть адаптированы для отслеживания границ подвыражений без потери в производительности. Библиотека regexp(3) восьмой редакции Unix реализовала подобный алгоритм в начале 1985, хотя, как объяснено ниже, она не была широко использована или даже замечена.

Неякорные сопоставления (unanchored matches). Эта статья предполагает, что р.в. сопоставляются целиком со строкой. На практике очень часто нужно найти во входной строке подстроку, которая соответствует р.в. Утилиты Unix традиционно возвращают самое длинное совпадение, которое начинается самым первым (с левого края). Неякорный поиск для выражения e является особым случаем извлечения совпадающей подстроки: он подобен поиску по р.в. .*(e).*, где первое .* ограничено как можно более короткой строкой.

Нежадные операторы (non-greedy operators). В традиционных р.в. Unix операторы повторения ?, * и + определены, чтобы искать как можно более длинное возможное совпадение при том, чтобы всё р.в. было сопоставлено: при проверке строки abcd по р.в. (.+)(.+), первое подвыражение (.+) найдёт abc, а второе - d. Сейчас такие операторы называются жадными. Perl представил операторы ??, *? и +? как нежадные версии, которые ищут как можно более короткие возможные совпадения с сохранением общего совпадения: при проверке строки abcd по р.в. (.+?)(.+?), первое подвыражение (.+?) найдёт только a, а второе - bcd. По определению, жадность оператора не может влиять на то, как в целом р.в. сопоставляет строку целиком; жадность влияет лишь на выбор границ подвыражений. Алгоритмы с возвратом позволяют реализовать нежадные операторы простым образом: сначала проверять более короткое совпадение перед проверкой более длинного. Например, в стандартной реализации с возвратом в e? сначала проверяется e, а потом проверяется вариант без него; при e?? используется другой порядок проверки. Варианты алгоритма Томпсона с проверкой границ подвыражений могут быть адаптированы под нежадные операторы.

Утверждения (assertions, позиционные проверки). Метасимволы традиционных р.в. ^ и $ могут рассматриваться в качестве утверждений о тексте рядом с ними: ^ утверждает, что предыдущим символом является символ новой строки (или начало строки), а $ утверждает, что следующим символом является символ новой строки (или конец строки). Perl добавил больше утверждений, таких как граница слова (\b), которое утверждает, что предыдущий символ является буквенно-цифровым, а следующий - нет, или наоборот. Perl так же обобщил эту идею на произвольные условия, называемые lookahead утверждениями: (?=re) утверждает, что текст после текущей позиции в строке совпадает с re, но при этом на самом деле не потребляет символов; (?!re) действует подобным образом, но утверждает, что текст не совпадает с re. Lookbehind утверждения (?<=re) и (?<!re) так же похожи, но утверждения делают для текста перед текущей позицией в строке. Простые утверждения вроде ^, $ и \b легко можно адаптировать в НКА, отложив совпадение для проверки на один байт. Обобщённые утверждения сложнее адаптировать, но, в принципе, могут быть закодированы в НКА.

Обратные ссылки (backreferences). Как упоминалось ранее, никто ещё не знает, как реализовать р.в. с обратными ссылками эффективно, при этом никто не доказал, что это невозможно. (Собственно, задача является NP-полной, что означает, что если кто-то найдёт эффективную реализацию, то это будет большой новостью в компьютерных науках, и получит приз в миллион долларов.) Самая простая и наиболее эффективная стратегия для обратных ссылок - использовать оригинальные awk и egrep, а не реализовывать их. Но это стратегия не является практичной: пользователи полагаются на обратные ссылки, как только однажды воспользовались ими. И обратные ссылки являются частью стандарта POSIX для р.в. Даже так, было бы разумным использовать симуляцию НКА Томпсона для большинства р.в., и использовать алгоритмы с возвратом только по необходимости. Особо умная реализация могла бы использовать оба подхода, обращаясь к алгоритмам с возвратом только для адаптации обратных ссылок.

Возврат с запоминанием (backtracking with memoization). Подход Perl'а к использованию запоминания для того, чтобы избежать экспоненциального взрыва в процессе возврата, когда только это возможно, вполне хороший. По крайней мере в теории он должен обеспечить поведение Perl'овых р.в. более близкое к НКА, чем к алгоритмам с возвратом. Однако запоминание не полностью решает проблему: она сама по себе требует объёма памяти примерно равным произведению размеров текста и регулярного выражения. Так же оно не предназначено для решения проблемы стекового пространства, используемого для возврата, которое линейно зависит от размера текста: у реализаций с возвратом сопоставление длинных строк обычно вызывает исчерпание стекового пространства:

$ perl -e '("a" x 100000) =~ /^(ab?)*$/;'
Segmentation fault (core dumped)
$

Символьные множества (character sets). Современные реализации р.в. обязаны работать с громадными множествами не-ASCII символов, таких как Юникод. Библиотека р.в. из Plan 9 реализует поддержку Юникода, запуская на каждом шаге НКА для одиночного Юникод-символа в качестве входящего символа. Эта библиотека отделяет запуск НКА от декодирования входных данных, т.о. один и тот же код сопоставления р.в. может быть использоваться как для UTF-8, так и для других входных данных с широкими символами.

История и ссылки

Майкл Рабин (Michael Rabin) и Дана Скот (Dana Scott) представили недетерминированный конечный автомат и концепцию недетерминизма в 1959 году [7], показав, что НКА могут быть симулированы с помощью (потенциально более крупными) ДКА, в которых каждое состояние ДКА соответствует множеству состояний НКА. (Они получили Премию Тьюринга в 1976 за представление концепции недетерминизма в своей работе.)

Р. МакНотону (R.McNaughton), Х. Ямаде (H.Yamada) [4] и Кену Томпсону (Ken Thompson) [9] обычно приписывают создание первых конструкций для преобразования р.в. в НКА, даже не смотря на то, что ни одна из работ не упоминает тогда ещё зарождающуюся концепцию НКА. Конструкция МакНотона и Ямады создаёт ДКА, а конструкция Томпсона создаёт машинный код для IBM 7094. Читая между строк можно увидеть скрытые конструкции НКА, лежащие в основе обеих работ. Конструкции НКА и р.в. отличаются лишь в том, как они кодируют сделанный НКА выбор. Подход, использованный выше, имитирующий Томпсона, кодирует варианты выбора через узлы явного выбора (выше они названы узлами Split) и немаркированные стрелки. Альтернативный подход, который часто приписывают МакНотону и Ямаде, заключается в том, чтобы избегать немаркированных стрелок, вместо них позволяя состояниям НКА иметь стрелки с одинаковой меткой. МакИлрой (McIlroy) [3] представил особенно элегантную реализацию этого подхода на языке Haskell.

Реализация Томпсона для р.в. была создана для его редактора QED, который запускался в ОС CTSS [10] на компьютере IBM 7094. Копию редактора можно найти в архивах исходных текстов CTSS [5]. Л. Питер Дейч (L.Peter Deutsch) и Батлер Лэмпсон (Butler Lampson) [1] разработали первую версию QED, но реализация Томпсона была первой, в которой использовались р.в. Денис Ритчи (Dennis Ritchie), автор ещё одной реализации QED, задокументировал раннюю историю развития редактора QED [8]. (Томпсон, Ритчи и Лэмпсон позже получили премию Тьюринга, но за работу, которая не связана ни с QED, ни с конечными автоматами.)

Работа Томпсона отметила начало длинной череды реализаций р.в. Томпсон решил не использовать свой алгоритм при реализации текстового редактора ed, который появился в первой редакции Unix (1971), или в его наследнике grep, который впервые появился в четвёртой редакции (1973). Вместо этого эти почтенные инструменты Unix использовали рекурсивный алгоритм с возвратом! Это было оправдано, потому что синтаксис р.в. был весьма ограничен: в нём не учитывались ни группирующие круглые скобки, ни операторы |, ? и +. egrep от Ала Ахо (Al Aho), который впервые появился в седьмой редакции (1979), был первым инструментом Unix, который предоставлял полный синтаксис р.в., используя предвычисленный ДКА. К восьмому изданию (1985) egrep вычислял ДКА на лету, как и в реализации, приведённой выше.

Во время написания текстового редактора sam [6] в начале 80х, Роб Пайк (Rob Pike) создал новую реализацию р.в., которую Дэйв Пресото (Dave Presotto) вынес в библиотеку, которая появилась в восьмой редакции. Реализация Пайка привнесла отслеживание подвыражений (submatch tracking) в эффективную симуляцию НКА, но, как и остальная часть исходных текстов восьмой редакции, не была широко распространена. Сам Пайк не сознавал, что его техникам была чем-то новым. Генри Спенсер (Henry Spencer) реализовал интерфейс библиотеки восьмой редакции с нуля, но используя алгоритм с возвратом, и выпустил свою реализацию в публичный доступ. Он стала очень широко использоваться, и в итоге послужил основой для медленных реализаций, упомянутых ранее: Perl, PCRE, Python и т.д. (В своё оправдание, Спенсер знал, что функции могут быть медленными и не знал, что существуют более эффективные алгоритмы. Он даже разместил предупреждение в документации: "Многие пользователи нашли скорость работы вполне адекватной, хотя замена внутренностей egrep на этот код была бы ошибкой.") Реализация р.в. от Пайка, расширенная поддержкой Юникода, была свободно доступной вместе с редактором sam в конце 1992, но особо эффективный алгоритм поиска по р.в. остался незамеченным. Сейчас этот код доступен во многих формах: как часть редактора sam, как библиотека р.в. из Plan 9, или отдельный пакет для Unix. Вилле Лаурикари (Ville Laurikari) независимо открыл алгоритм Пайка в 1999, так же разработав теоретическое обоснование [2].

Наконец, любое обсуждение р.в. было бы неполным без упоминания книги Джеффри Фридла (Jeffrey Friedl) "Mastering Regula Expressions", возможно, самого популярного справочника среди современных программистов. Книга Фридла учит программистов тому, как лучше всего использовать современные реализации р.в., но не тому, как лучше всего реализовать их. Тот небольшой текст, который посвящён вопросам реализации, увековечивает широко распространённое мнение, что рекурсивный алгоритм с возвратом является единственным способом симулировать работу НКА.

Заключение

Поиск по регулярным выражениям может быть простым и быстрым, используя техники на основе конечных автоматов, которые известны на протяжении десятилетий. В противоположность этому, Perl, PCRE, Python, Ruby, Java и многие другие языки используют реализации на основе рекурсивного алгоритма с возвратом (recursive backtracking), которые являются простыми, но могут быть мучительно медленными. За исключением обратных ссылок (backreferences), возможности, предоставляемыми этими реализациями, могут быть предоставлены и реализациями на основе автоматов, причём со значительно более высокими и более постоянными скоростями.

Следующая статья в этой серии, "Поиск по регулярным выражениям: Подход с Виртуальной Машиной", посвящена извлечению подвыражений (submatch extraction) на основе НКА. Третья статья, "Регулярные выражения в дикой природе" исследует продакшн реализации. Четвёртая статья, "Поиск по регулярным выражениям с помощью триграм индекса", объясняет, как реализован Google Code Search.

Благодарности

Lee Feigenbaum, James Grimmelmann, Alex Healy, William Josephson, и Arnold Robbins вычитывали черновики этой статьи и сделали очень много полезных предложений. Rob Pike разъяснил некоторые моменты в истории его реализации поиска по регулярным выражениям. Спасибо им всем.

Список ссылок

[1] L. Peter Deutsch and Butler Lampson, “An online editor,” Communications of the ACM 10(12) (December 1967), pp. 793–799. http://doi.acm.org/10.1145/363848.363863

[2] Ville Laurikari, “NFAs with Tagged Transitions, their Conversion to Deterministic Automata and Application to Regular Expressions,” in Proceedings of the Symposium on String Processing and Information Retrieval, September 2000. http://laurikari.net/ville/spire2000-tnfa.ps

[3] M. Douglas McIlroy, “Enumerating the strings of regular languages,” Journal of Functional Programming 14 (2004), pp. 503–518. http://www.cs.dartmouth.edu/~doug/nfa.ps.gz (preprint)

[4] R. McNaughton and H. Yamada, “Regular expressions and state graphs for automata,” IRE Transactions on Electronic Computers EC-9(1) (March 1960), pp. 39–47.

[5] Paul Pierce, “CTSS source listings.” http://www.piercefuller.com/library/ctss.html (Thompson's QED is in the file com5 in the source listings archive and is marked as 0QED)

[6] Rob Pike, “The text editor sam,” Software—Practice & Experience 17(11) (November 1987), pp. 813–845. http://plan9.bell-labs.com/sys/doc/sam/sam.html

[7] Michael Rabin and Dana Scott, “Finite automata and their decision problems,” IBM Journal of Research and Development 3 (1959), pp. 114–125. http://www.research.ibm.com/journal/rd/032/ibmrd0302C.pdf

[8] Dennis Ritchie, “An incomplete history of the QED text editor.” http://plan9.bell-labs.com/~dmr/qed.html

[9] Ken Thompson, “Regular expression search algorithm,” Communications of the ACM 11(6) (June 1968), pp. 419–422. http://doi.acm.org/10.1145/363347.363387 (PDF)

[10] Tom Van Vleck, “The IBM 7094 and CTSS.” http://www.multicians.org/thvv/7094.html