Вступление.

Многим сервисам критически важно иметь информацию о местонахождении подключенных устройств. Кикшеринг — не исключение. Нам в Whoosh нужно отслеживать каждый отдельно взятый самокат в каждый отдельно взятый момент времени. Поэтому все наши самокаты оснащены навигационным приемником, или как его еще называют, GNSS модулем. Однако, технология спутниковой навигации, несмотря на свою чрезвычайную популярность обладает и рядом недостатков. Например, навигационный приемник относительно легко сбить с толку, то есть заглушить или исказить принимаемый им сигнал. В результате, получаемое пользователем местоположение не будет иметь ничего общего с действительностью. И бороться с этим достаточно сложно. Поэтому на помощь спутниковой навигации приходят другие, альтернативные способы определения местоположения, такие как инерциальные навигационные системы (ИНС), определение местоположения по базовым станциям и WiFi точкам и т.д.

И сегодня мы поговорим об ИНС, а точнее об одном из необходимых элементов подобных систем — магнитометре, а еще точнее о том, как его калибровать.

Коротко о магнитометре.

Датчик, как правило трехосевой, измеряет магнитное поле, по сути трехмерный компас.

Историю создания, особенности строения, варианты исполнения и прочее предлагаю опустить. Скажем лишь только, что в контексте данной статьи речь идёт о MEMS магнитометрах, наподобие тех, что стоят в наших смартфонах. Обычно такие магнитометры делают на основе эффекта Холла или силы Лоренца.

А зачем вообще калибровать?

В идеальном мире идеальный компас, использующий идеальный магнитометр, видел бы только магнитное поле земли и показывал бы всегда идеально на магнитный север. Но на практике в показаниях магнитометра, в нашем случае установленного на печатной плате, присутствуют магнитные поля соседних индуктивностей и всех проводников, которые под действием магнитного поля земли и иных источников также намагничиваются. Собственно это и есть два основных вида помех, которые еще называют hard-iron и soft-iron distortions [1].
А названы они так в честь двух разновидностей ферромагнетиков — магнитотвердых и магнитомягких.

Первые по сути своей постоянные магниты, их присутствие по соседству с магнитометром приводит к тому, что он измеряет значение магнитного поля земли + значения магнитных полей этих самых магнитотвердых материалов. Вот только при вращении магнитометра в пространстве, вектор магнитного поля земли вращается относительно магнитометра, а вот hard-iron помехи остаются неизменными (так как когда мы вращаем магнитометр, положение севера относительно него меняется, а вот положение соседних с ним на плате элементов — нет). Этот факт и поможет нам в дальнейшем при компенсации hard-iron помех.

А что касаемо soft-iron, то их создают все проводники, находящиеся неподалеку от магнитометра. Они намагничиваются в магнитном поле земли и, тем самым, имеют свое собственное магнитное поле, однако оно, в отличие от hard-iron, изменяется при вращении магнитометра в пространстве в соответствии с этим вращением.

В рамках этой статьи мы осознанно будем игнорировать soft-iron помехи, потому что по сравнению с hard-iron они не столь существенно влияют на работу магнитометра.

А что будет, если вообще не калибровать?

Вполне резонный вопрос. Магнитометр чаще всего используется в компасах, и компас на основе не откалиброванного магнитометра скорее всего будет указывать всегда в одном и том же направлении. Поэтому некоторые, возможно, сталкивались с тем, что иногда приходилось крутить телефон восьмеркой, чтобы навигатор нормально работал. А те, кто знаком с квадрокоптерами, знают, что одним из элементов предполетной подготовки является вращение коптера вручную, причём как в обычном положении, так и боком. Собственно, это делается как раз для того, чтобы откалибровть датчики, установленные на борту, в том числе и магнитометр.

Вращать самокат перед каждой поездкой — это, конечно, идея, но не думаю, что она придется по душе нашим юзерам.

Какие способы калибровки существуют?

Хотел бы я дать ссылку на Вики, где были бы кратко и лаконично расписаны существующие способы калибровки магнитометра, но там пусто.

А вообще, давайте отложим в сторону Google и chatGPT и попробуем решить эту задачу сами. Для того, чтобы было на что опереться, я записал данные с магнитометра, покрутив им пару хороших восьмерок.

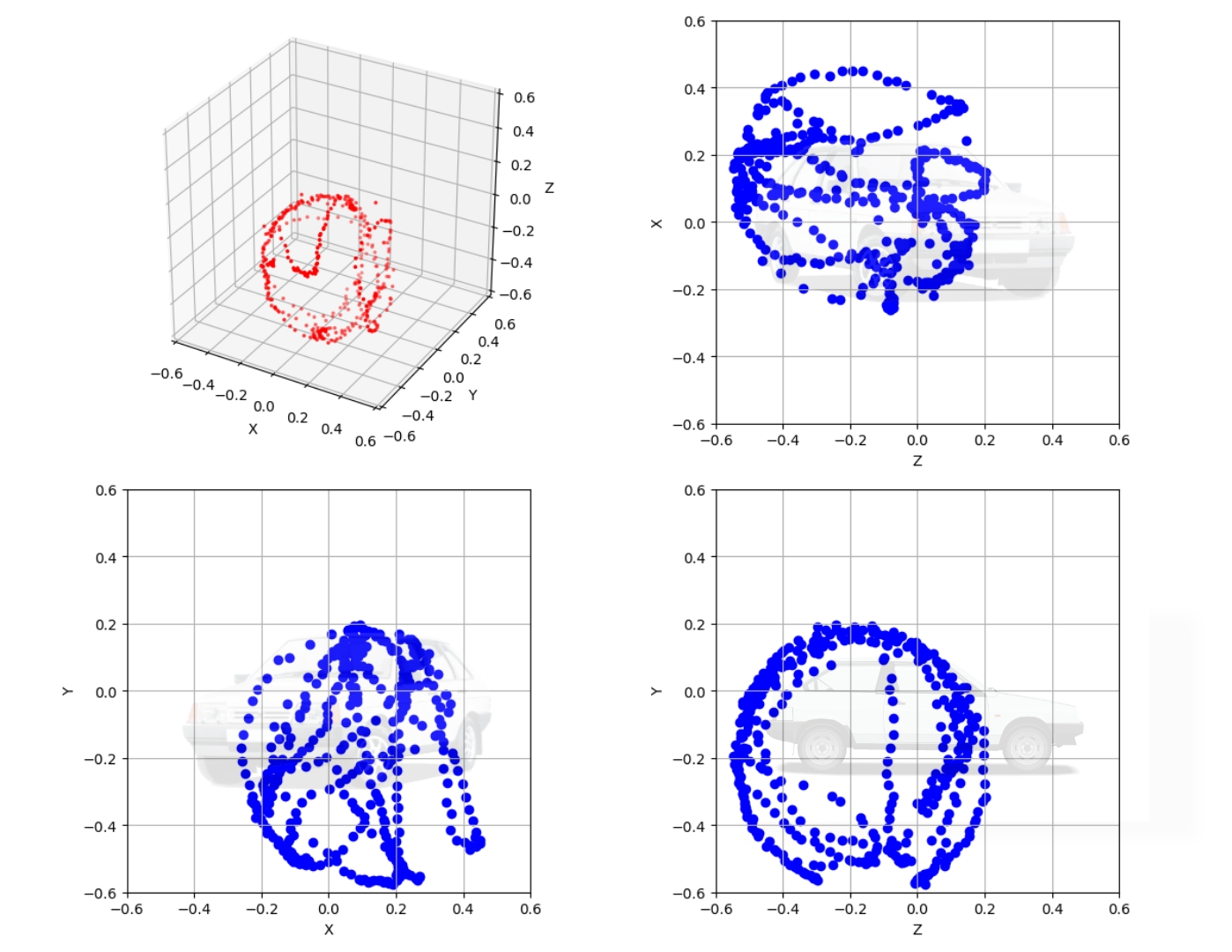
Дано: трехосевой датчик, которым нужно измерить конкретный вектор, однако мы знаем, что помимо этого вектора в измерениях датчика присутствует некая постоянная помеха (soft-iron осознанно игнорируем). Как мы писали ранее, особенность этой помехи в том, что ее положение в системе координат датчика неизменно, в то время как положение искомого вектора неизменно относительно глобальной системы координат.

Решение: Для начала давайте ограничимся двумя осями X и Y. Для любого произвольного положения датчика в пространстве, измерение (допустим по оси X) будет содержать помехи и какое-то значение искомого вектора . Если мы будем вращать датчик в пространстве вокруг оси Z, то все измерения будут лежать на окружности (эллипсе, если всё-таки не игнорировать soft-iron) со смещенным относительно нуля центром. Наша задача найти это смещение, и кажется что сделать это можно просто взяв для каждой из осей. Так и сделаем.

Для данных с графиков выше, найдем значение смещения по всем осям:

Теперь, если применить полученные смещения, то наша сфера окажется приблизительно в точке , собственного этого мы и добивались.

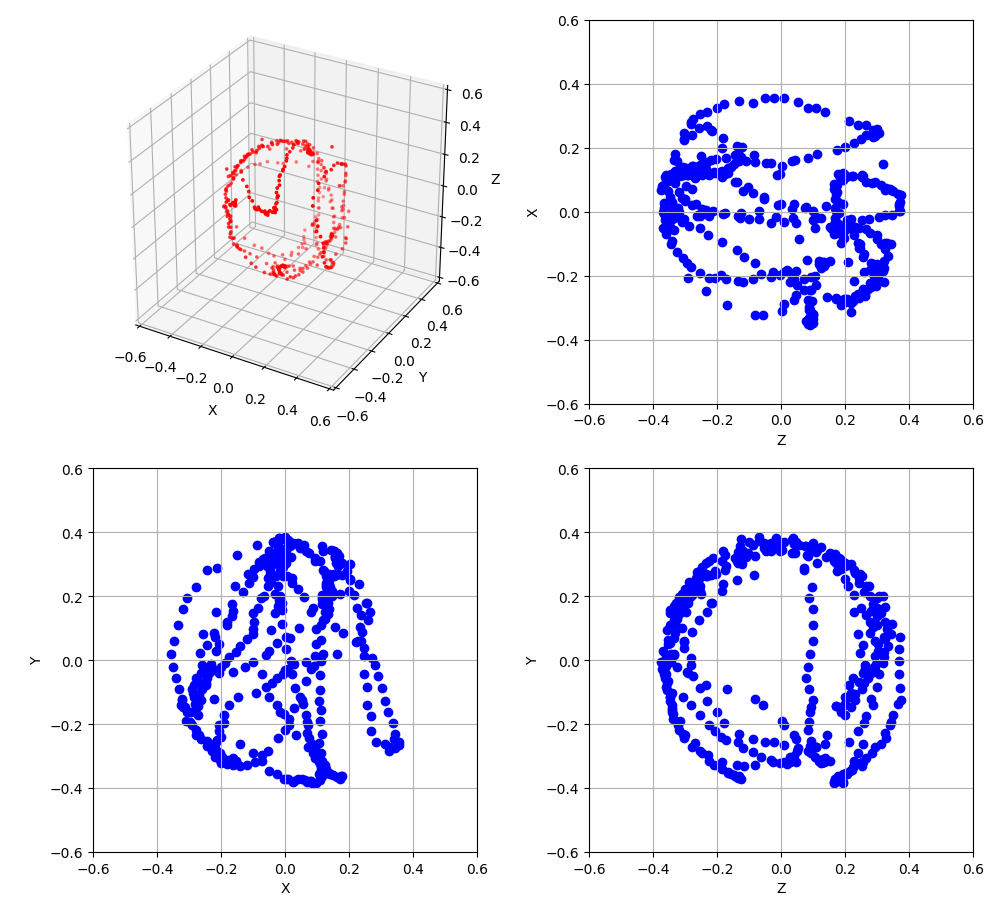
Итого: мы изобрели простейший метод калибровки, назовем его “кручу-верчу, откалибровать хочу”. А теперь прежде чем подавать заявку на патент и звонить маме, чтобы сказать ей, что ты не зря учился в универе шесть лет, давайте все же загуглим, какие существуют нормальные методы калибровки. (Хотя маме позвонить все равно можно, это никогда не лишнее)

В англоязычной литературе самый часто встречаемый способ калибровки магнитометра это ellipsoid fitting. Например вот здесь [2] и здесь [3]

Если вкратце, то при достаточном количестве измерений, они +/‑ укладываются на поверхность эллипсоида. И если найти параметры этого эллипсоида, то это и будут наши калибровочные коэффициенты, причем как hard‑iron так и soft‑iron. Для этого обычно используют метод наименьших квадратов. Правда точность зависит от того, насколько равномерно измерения будут распределены по поверхности эллипсоида, а чтобы этого достичь нужно вращать магнитометр по всем трем осям, в нашем случае вращать вместе с самокатом (который весит 30+кг), иначе пропадает смысл калибровки. (Лео, прости) Но делать мы этого не станем, хотя я где‑то слышал, что если в день два раза такую калибровку делать, то спина вообще болеть не будет.

Ищем дальше.

Много слов, мало дела. Давай калибровать.

Ладно, в целом кажется, что тут вся суть во вращении. То есть пока хоть сколько-нибудь самокат не покрутишь, откалибровать магнитометр никак не получится. А что если использовать вращения, которые совершает пользователь во время поездки? Да, конечно, редко кто ездит на боку или вверх ногами, но и ехать постоянно прямо тоже сложно. Иными словами какие-то вращения в плокости дороги (то есть повороты) у нас есть, и мы можем откалиброваться в одной поездке, а уже в следующей у нас будет рабочий компас.
Звучит заманчиво.

Для этого нам нужны измерения получаемые с датчика во время поездки, причем желательно накопить их как можно больше. Плюс по итогам поездки эти данные нужно где-то обработать, причем весь массив одновременно.

Уже не так заманчиво.

Но все же попробуем. Сделаем прошивку для скутера, которая будет во время поездки (пока что тестовой) собирать данные магнитометра и засылать их на бэкенд.

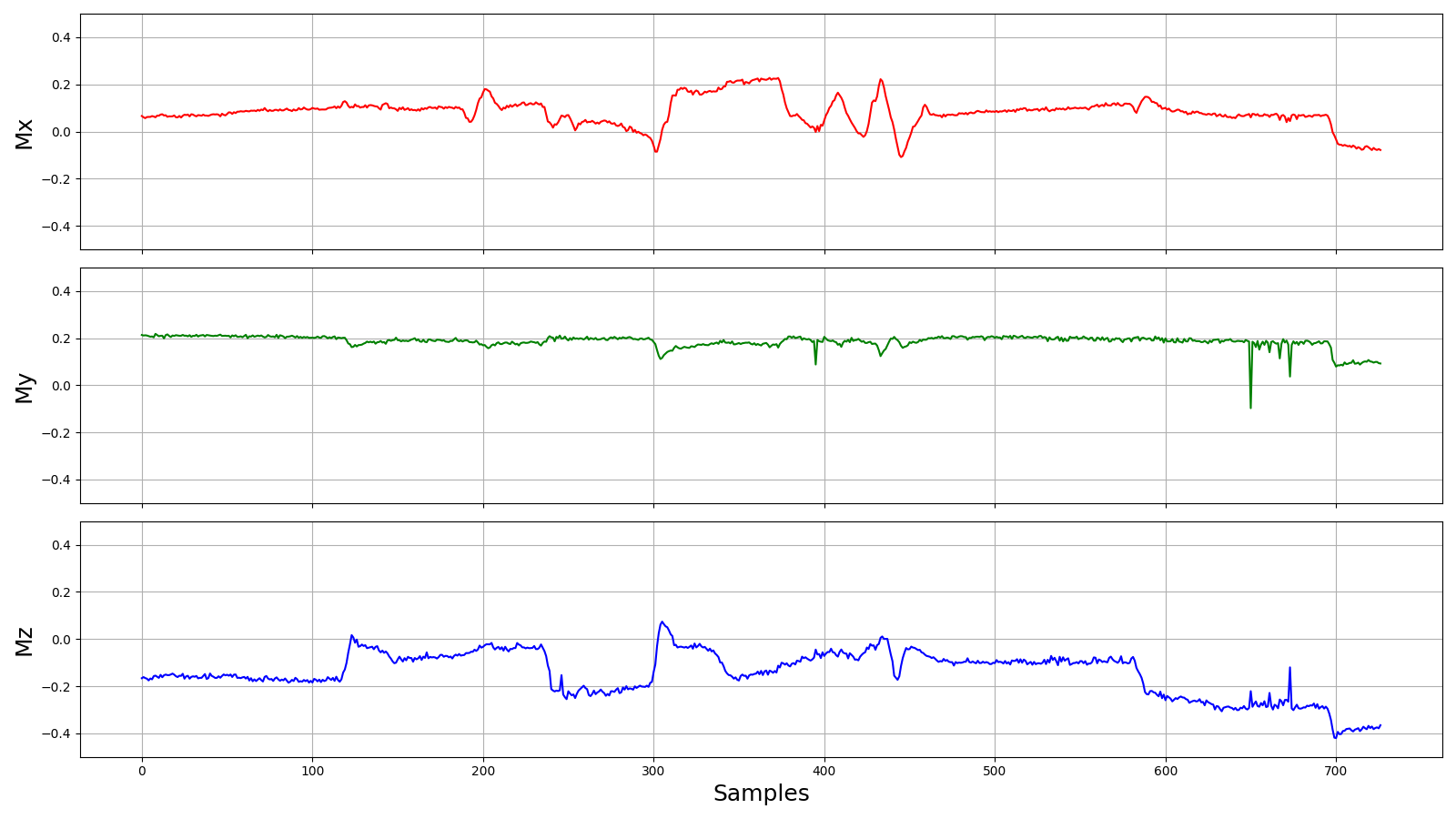
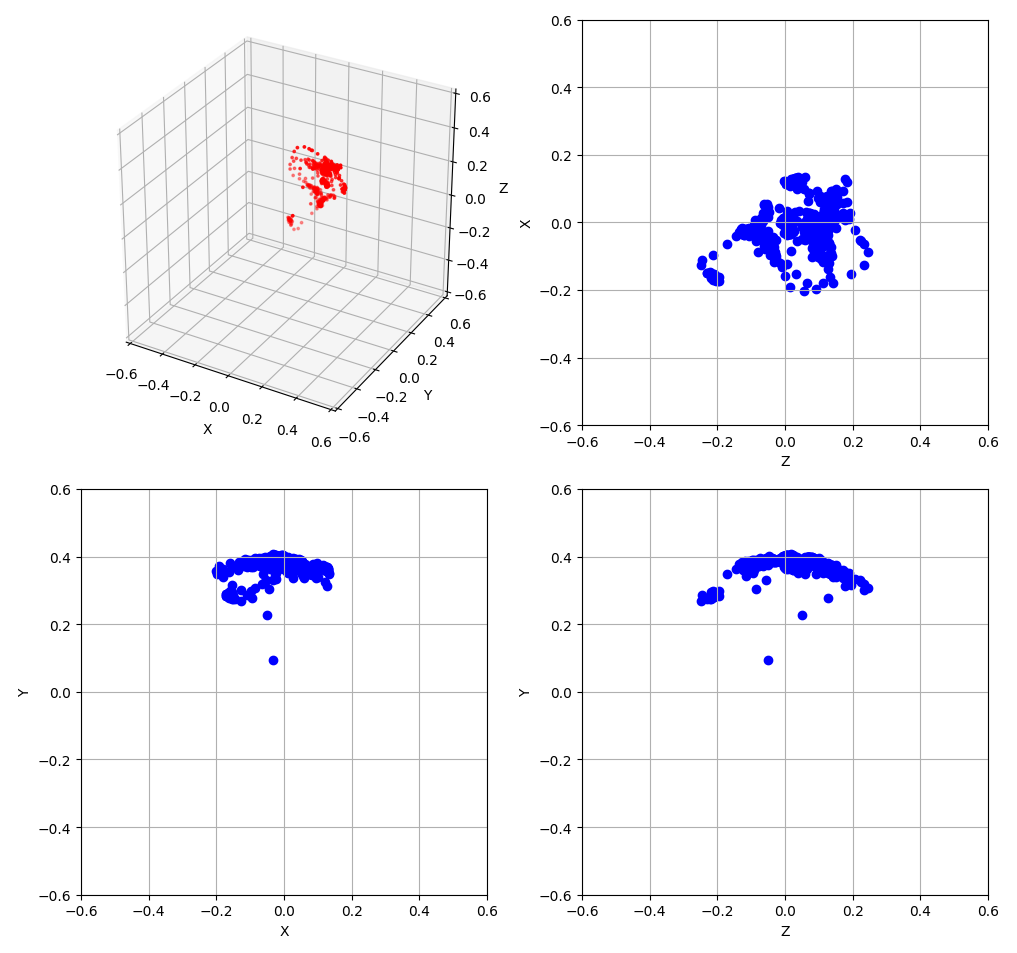
Нетрудно заметить разницу с данными, которые мы получили при вращении магнитометра восьмёрками. Скорее всего по одной из осей нормальную калибровку провести не удастся. Но вдруг для того, чтобы знать где север нам этого и не нужно? Давайте проверим. Примеров реализации ellipsoid fitting в сети достаточно, поэтому возьмем один из них.

from scipy import linalg

def non_rotated_ellipsoid_fit(x, y, z): # будем считать, что эллипсоид не повернут
    x = x[np.newaxis].T
    y = y[np.newaxis].T
    z = z[np.newaxis].T

    D = np.hstack((x*x + y*y - 2*z*z, x*x + z*z -
                   2*y*y, 2*x, 2*y, 2*z, 1 + 0*x))
    d2 = x*x + y*y + z*z
    u = np.linalg.inv(D.T@D)@D.T@d2
    v = np.array([u[0] + u[1] - 1, u[0] - 2*u[1] - 1, u[1] - 2*u[0] - 1])
    v = np.vstack((v, [0], [0], [0], u[2:]))
    A1 = np.hstack((v[0], v[3], v[4], v[6]))
    A2 = np.hstack((v[3], v[1], v[5], v[7]))
    A3 = np.hstack((v[4], v[5], v[2], v[8]))
    A4 = np.hstack((v[6], v[7], v[8], v[9]))
    A = np.vstack((A1, A2, A3, A4))
    v789 = np.vstack((v[6], v[7], v[8]))
    ofs = -np.linalg.inv(A[0:3, 0:3])@v789
    Tmtx = np.eye(4)
    Tmtx[3, 0:3] = ofs.T
    AT = Tmtx@A@Tmtx.T
    ev, rotM = np.linalg.eig(AT[0:3, 0:3]/-AT[3, 3])
    gain = np.sqrt(1/np.abs(ev))
    signs = np.sign(ev)
    gain = gain*signs

    return ofs, gain, rotM, ev

ofs, _, _, _ = non_rotated_ellipsoid_fit(mx, my, mz)
print(', '.join([f'{x:.3f}' for x in ofs[:, 0]]))

Получаем наши смещения: .
То есть по тем двум осям, в которых у нас присутствовали изменения по мере поездки, мы получили более-менее нормальные калибровочные коэффициенты.

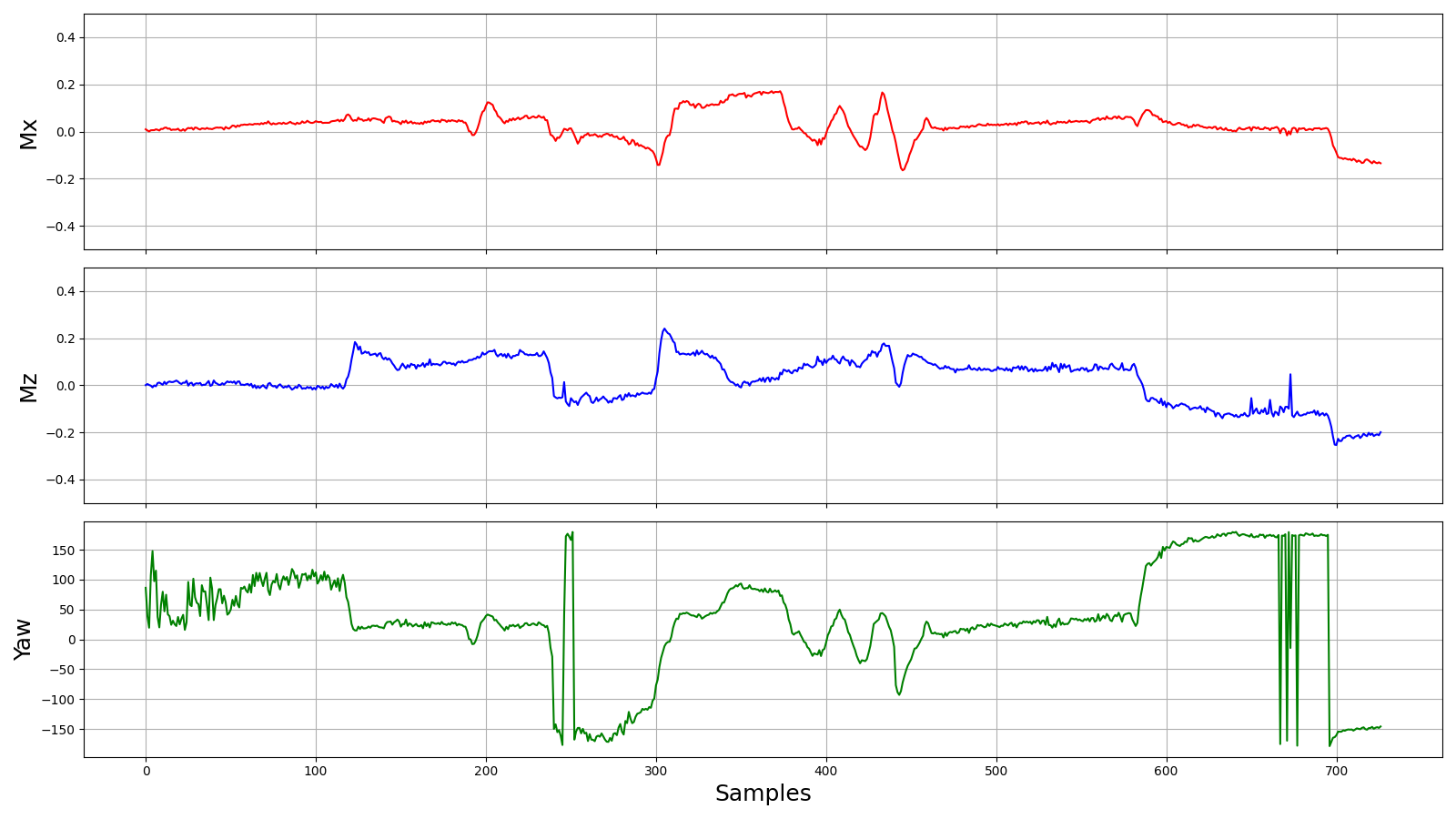
На графике выше я откалибровал оси X и Z, а также добавил график угла курса посчитанного “в лоб” как arctan значений mx и mz, и он даже немного похож на правду.

В целом, с этим можно жить. Хоть жить долго и счастливо не получится. И на то есть несколько причин:

• передача этих данных на бэк генерирует много трафика, здесь нужна какая-то оптимизация;

• при относительно прямых поездках коэффициенты будут рассчитаны некорректно, нужна проверка;

• для повышения точности неплохо бы считать по нескольким поездкам, тогда нужно где-то хранить эти данные.

В целом, решив задачу сжатия исходных данных без потери качества определения калибровочных коэффициентов, мы решим и оставшиеся проблемы. То есть, если данных будет меньше, то и за трафик вроде уже не так страшно, да и хранить можно больше поездок при том же объеме в хранилище. Хорошо, а как будем тогда сжимать?

С точки зрения калибровки, нам интересны именно вращения, то есть десять одинаковых измерений нам точности не добавят, следовательно можно отбрасывать близкие друг к другу измерения. Также, нам известны пределы измерения нашего датчика, то есть +100500 Гс мы никак не получим.

Имея все это ввиду, как бы вы подошли к этой задаче? Ниже опишу, как мы решили это сделать.

Возьмем пределы измерений по всем трем осям, и разобьём их на конечное число отрезков. Так, например, по оси X диапазон возможных значений лежит от -4 до +4, учитывая, что точность в несколько тысячных нам ни к чему (по сути это все равно будет +/- шум), мы можем этот диапазон разбить, например, на 800 отрезков. И так по всем трем осям. Так мы получим большой куб, разбитый на 512 000 000 маленьких кубиков. А чтобы еще больше все запутать, давайте каждому маленькому кубику поставим в соотвествие некий индекс, который состоит из трех чисел: порядкового номер отрезка, в котором находится кубик по оси X, а также по Y и по Z. Предвкушаю вопрос: ЗАЧЕМ? Попробую объяснить на примере.

data = [
    {'Mx': 0.917372, 'My': -0.000366, 'Mz': 0.420539},
    {'Mx': 0.899013, 'My': 0.004562, 'Mz': 0.419935},
    {'Mx': 0.916934, 'My': -0.001366, 'Mz': 0.420690}
]

for item in data:
    print(
        int((item['Mx'] + 4) * 100),
        int((item['My'] + 4) * 100),
        int((item['Mz'] + 4) * 100)
    )

491 399 442
489 400 441
491 399 442

Видно, что первое и третье измерения, хоть и отличаются по своим исходным значениям, но имеют абсолютно одинаковые индексы, поэтому первое мы можем оставить, а третье отфильтровать.

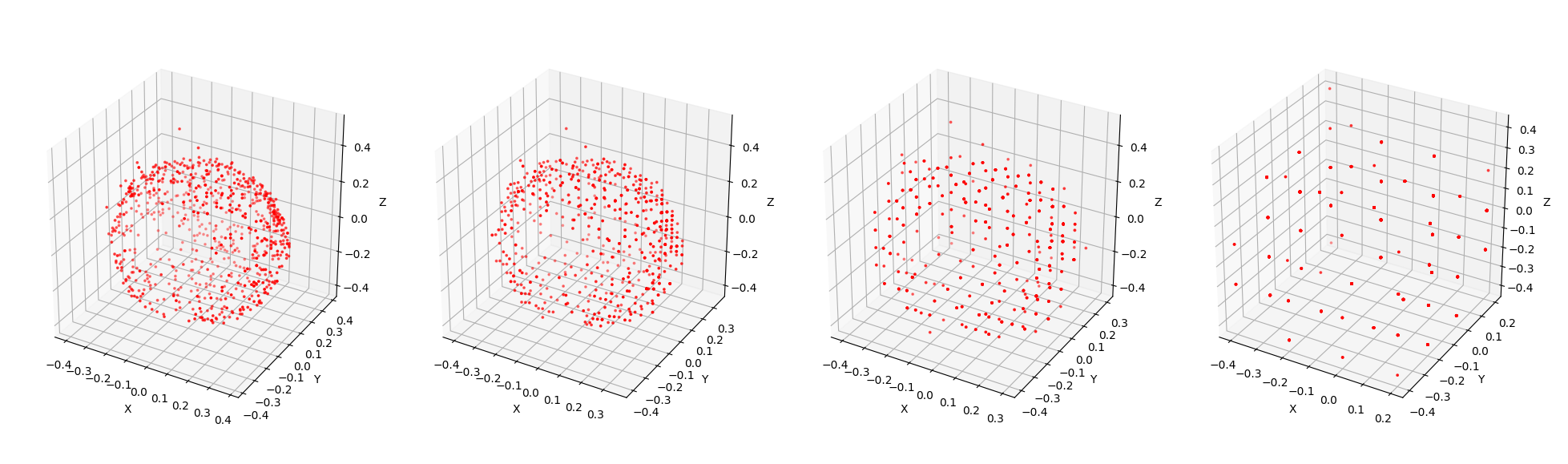
Итого. Мы можем реализовать калибровку магнитометра, используя отфильтрованные и преобразованные данные, записанные в поездках, передавая их на бэкенд и обрабатывая там, а затем возвращая полученные коэффициенты обратно на самокаты. При этом нам еще необходимо ко всему этому прикрутить валидацию полученных коэффициентов, а также автоматическую перекалибровку…

Ясно, понятно. Какие еще есть варианты?

Пока я искал существующие варианты калибровки, я несколько раз натыкался на методы в которых также используются другие датчики, такие, как например гироскоп. А также встречал методы, которые не требуют сбора большого массива данных, а работают как бы на лету.
Ну а что? Это было бы замечательно, не нужно ничего никуда пересылать, собирать и так далее. Все происходит непосредственно на самокате и при этом работает, даже если не крутить его во все стороны, а просто ездить на нем.

Две работы меня особенно заинтересовали, там используются показания гироскопа и расширенный фильтр Калмана [4] и [5].

Вектора, матрицы и много математики. Ну что ж.

Не будем вдаваться в детали относительно фильтра Калмана, про него и так уж слишком всего на хабре, попробуем лишь в общих чертах описать, что здесь происходит.

Мы уже выяснили, что для калибровки магнитометра нам необходимы вращения, но если мы не хотим без разбора вращать самокат во все стороны, то как нам быть?

А что если мы будем знать куда именно мы вращаем, поможет ли это с калибровкой?

Да, и именно тут нам пригодится гироскоп.

В публикации [4] основой предложенного метода является зависимость между показаниями гироскопа и магнитометра:

где - откалиброванные показания магнитометра, - номер итерации, - период времени между итерациями, а - матрица, состоящая из показаний гироскопа на предыдущей итерации :

Таким образом, нам по сути не столь важно в каком положении в пространстве магнитометр находился в предыдущей итерации. Однако, зная значение вектора , и зная по гироскопу как всё обернулось, мы можем предсказать новое значение . Причем работает это только для откалиброванного магнитометра, то есть если мы возьмем в качестве вектора состояния откалиброванные показания магнитометра и значения помех, то задача нашего фильтра сводится к тому, чтобы определить при каких значениях помех, зависимость выше будет выполняться.

Единственное, так как у нас есть и гироскоп и акселерометр, мы можем использовать показания с фильтра Маджвика (его мы уже реализовали), в котором они объединены. В публикации [5] как раз именно так и сделано, только используется фильтр Махони, но это не принципиально, главное, что мы можем выразить через и . То есть, вместо у нас будет:

,
где ,

а - матрица ориентации в пространстве.

Так, а что в итоге получается?

Для начала попробуем реализовать это на python, правда с одним небольшим отличием от того, что вы можете видеть в публикациях: мы уберем W, совсем, потому что эта матрица отвечает за soft-iron искажения, а их мы игнорируем. Это незначительно понизит точность калибровки, однако позволит при этом уменшить в два раза размерность некоторых векторов и матриц. Если бы реализовывать этот алгоритм нужно было бы на python, я бы скорее всего не заморачивался, from scipy import linalg и в путь, но наша конечная цель — это рабочий алгоритм на IoT модуле, то есть на языке C, причем на микроконтроллере, поэтому оптимизируем всё, что можно.

Сначала инициализируем наш фильтр:

Этап предсказания:

Этап корректировки:

Что означает и представляет из себя каждая матрица можно почитать здесь, на мой взгляд это одна из самых понятных статей по фильтру Калмана на хабре.

В итоге наш фильтр в качестве вектора состояния имеет откалиброванные показания магнитометра и калибровочные коэффициенты (смещения по всем трем осям). На этапе предсказания он определяет, каков будет новый вектор состояния исходя из матрицы , которая характеризует изменение положения в пространстве относительно предыдущего состояния. На этапе корректировки он расчитывает ошибку предсказания. Иными словами, он, используя новые неоткалиброванные измерения, определяет то, насколько промахнулся с предсказанием. А затем полученную ошибку домножает на специальный коэффициент усиления и корректирует свое предсказание. Таким образом, каждое, даже самое незначительное изменение положения магнитометра в пространстве, приближает нас к определению калибровочных коэффициентов, то есть таких значений b, при которых выполняется ,
где

Приведем для сравнения калибровочные коэффициенты, полученные разными методами и для разных ситуаций.

По таблице видно, что результаты работы обоих методов калибровки примерно схожи, но при этом если обратить внимание на данные по тестовой поездке, то можно заметить, что фильтр Калмана позволяет определять еще и смещение по оси, по которой особо не было вращений.

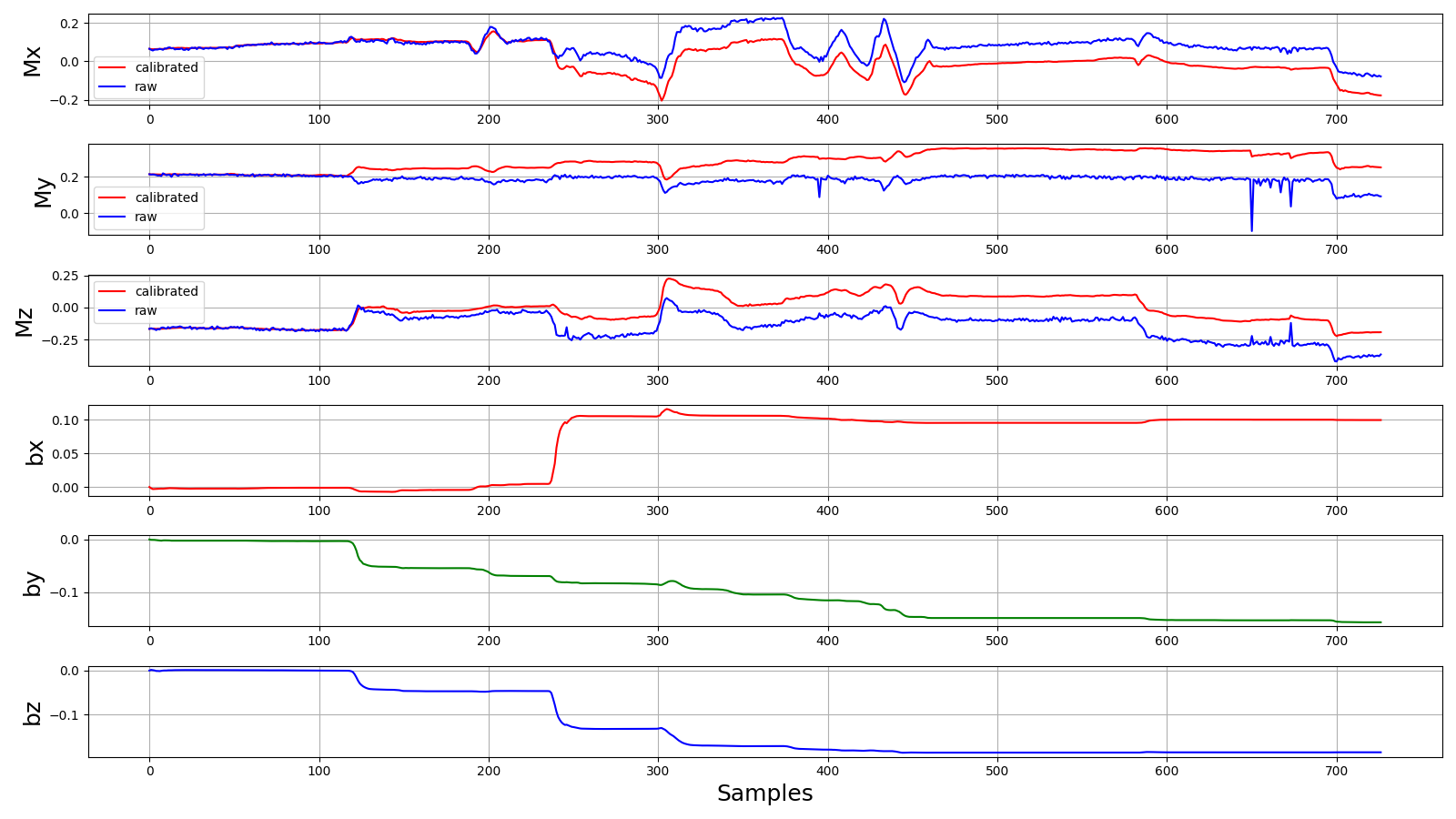
На первых трех графиках показаны первые три составляющие вектора состояния фильтра (то есть откалиброванные значения) и сырые данные магнитометра. На последних трех — последние три составляющие вектора состояния (то есть смещения по всем трем осям). Хорошо видно, как по мере вращений вокруг той или иной оси фильтр подправляет определенные им смещения.

Ниже приведу аналогичные графики, но уже для множества вращений вокруг всех трех осей.

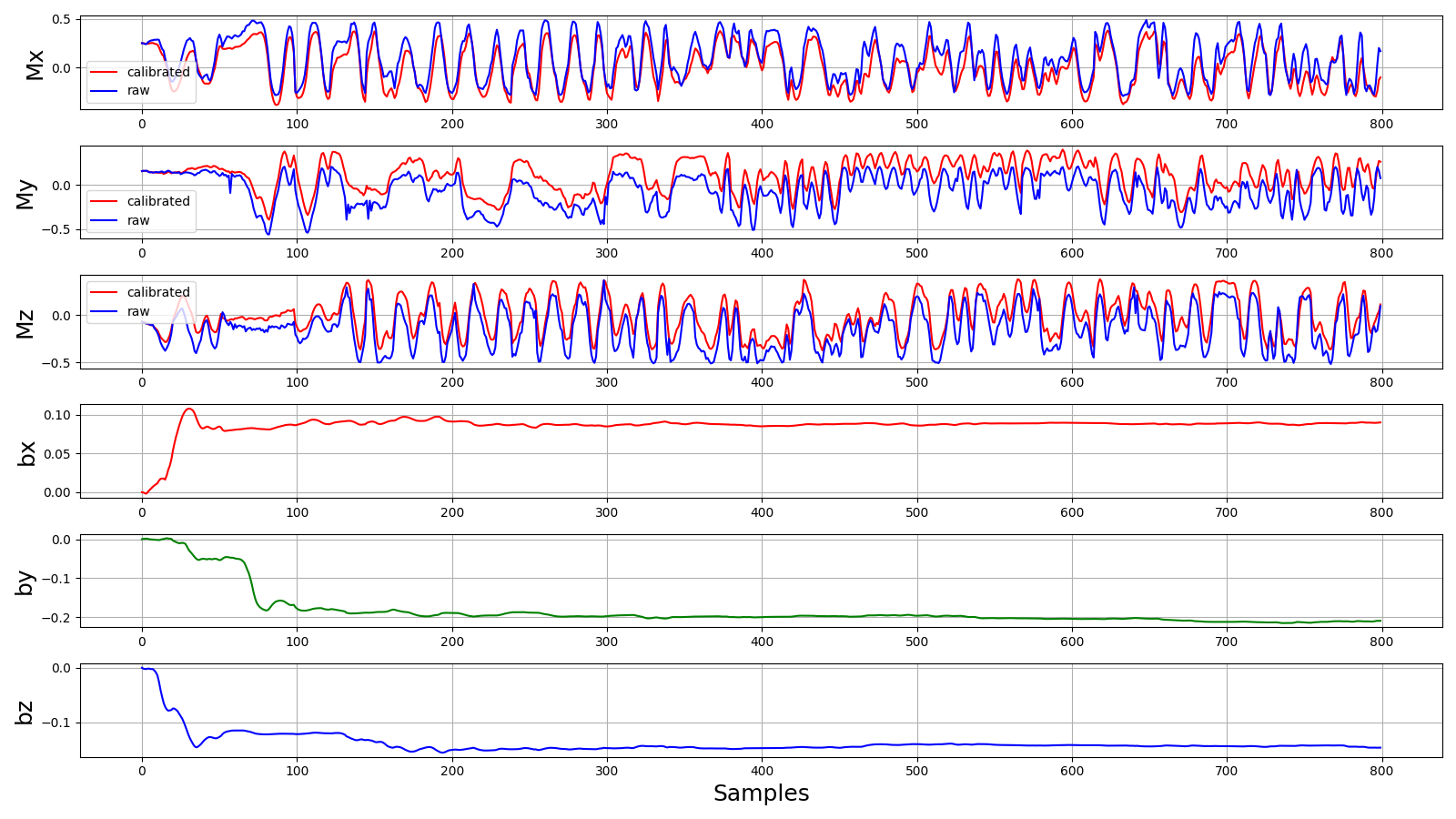
Здесь также видно, что после определенного количества вращений, фильтр как бы сходится к конкретным значениям смещений, это как раз именно то, к чему мы и стремились. Успешный успех.

Осталось только перенести это с Python на Си, но здесь ничего особенно интересного, поэтому лишь укажу ссылку на проект, который служил в качестве примера реализации библиотеки с матрицами.

Если после всех этих матриц и графиков вы уже забыли, ради чего всё это, то я вам напомню: нам нужен компас. Причем не просто для того, чтобы знать где север, а для того, чтобы, используя дополнительную информацию (например, скорость передвижения), определять местоположение. Иначе говоря, зная в каждый момент времени в каком направлении мы движемся и с какой скоростью, мы можем построить траекторию движения, то есть трек. А если мы при этом еще и знаем откуда стартовали, то мы (с определенной погрешностью) можем сказать куда мы прибыли.

В качестве примера рассмотрим ситуацию, когда пользователь взял самокат в поездку, но по каким-то причинам у нас не работает GPS, и мы знаем только координаты парковки, с которой началась поездка.

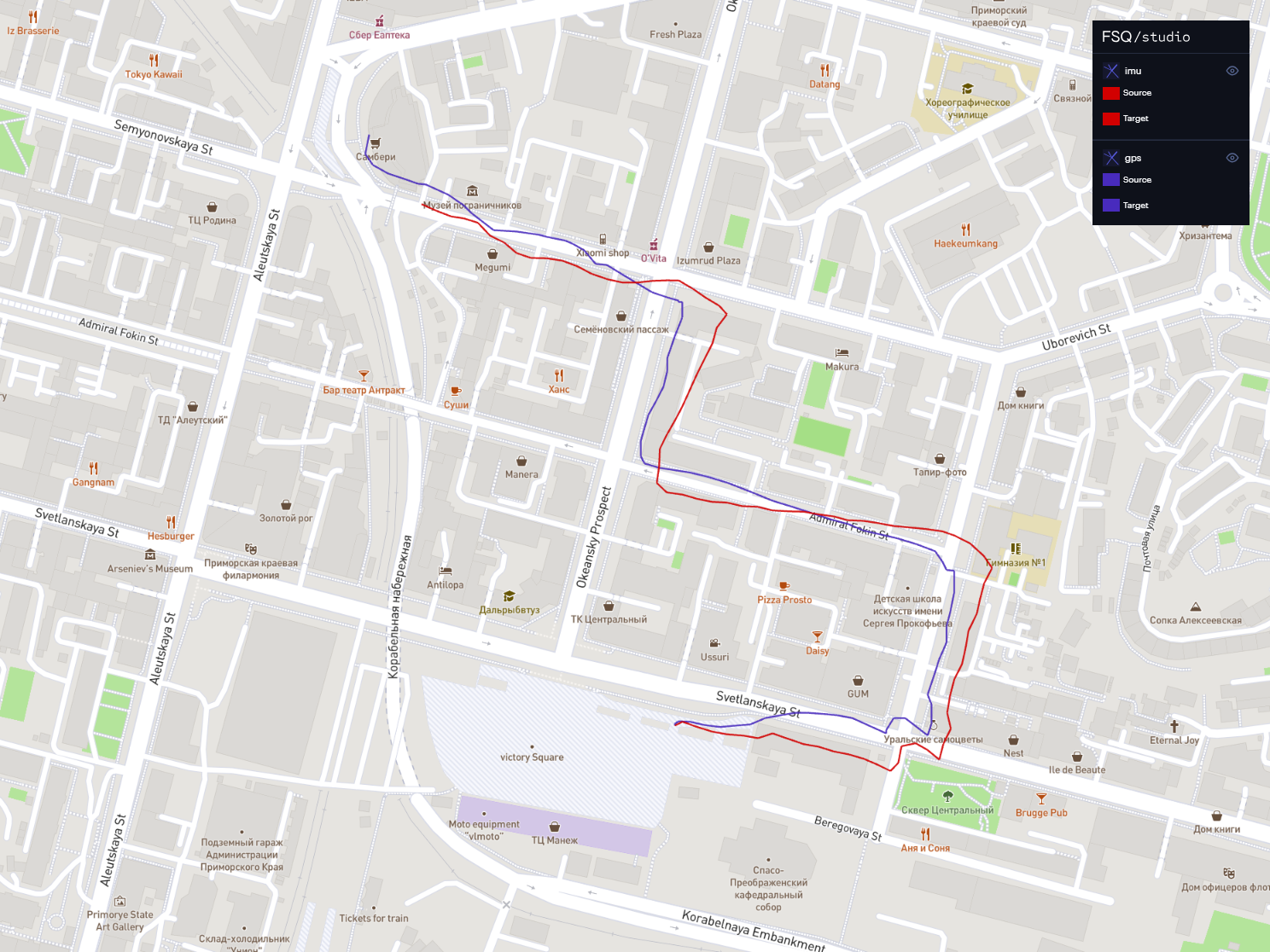
На данной карте, внизу, там откуда начинаются обе линии, находится парковка, с которой пользователь начал поездку. Синим обозначен трек по GPS, а красным — трек, который мы построили по компасу и информации о скорости движения (её мы получаем от контроллера мотор-колеса). Даже если бы в этой поездке не было никаких GPS координат, мы бы все равно имели информацию о его местоположении, причем с точностью в пару десятков метров (что очень даже прилично и всегда лучше, чем совсем ничего).

Послесловие

Помните, как в фильмах с Джеки Чаном, в конце во время титров показывали смешные моменты и неудачные дубли? Так вот…

Изначально, как только я перевел формулы в код на python, казалось, что оно заработало, НО при определенных вращениях фильтр вёл себя мягко говоря странно: вместо того, чтобы стремиться к каким-то фиксированным значениям смещений, он начинал их уменьшать или увеличивать, пока они не убегали в бесконечность.

Я очень долго искал в чем может быть проблема, проверил все (почти все) уравнения и в какой-то момент уже почти отчаялся. Покоя не давал тот факт, что в обеих публикациях на основе которых я пытался реализовать фильтр, был рабочий пример с данными и графиками. Значит, лыжи все-таки едут…

В одной из публикаций наряду со списком авторов был указан адрес электронной почты, на который я написал письмо. Но ответа не последовало, впрочем сама идея попытки связаться с авторами забрезжила в моей голове лучиком надежды.

Поэтому я решил не сдаваться и начал сталкерить пытаться найти контакты всех ученых, чьи имена встречались в интересующих меня публикациях. Никаких полуночных смсок не было, не переживайте, всё ограничивалось одним электронным письмом с вопросами по реализации алгоритма (даже без упоминания половины наследства от африканского принца в качестве платы за помощь). И на удивление, буквально через день мне пришел ответ от Ke Han, причем из небезызвестной компании Intel, с прикрепленным архивом, в котором было несколько матлабовских скриптов и csv-файлы с тестовыми данными, которые использовались при написании публикации [4]. На радостях я побежал быстро сверять свой код с тем, что было в их скриптах и прогонять их тестовые данные. И всё это только чтобы обнаружить, что мой код на питоне по-прежнему не работает… Короче, не помогло. Хотя я искренне не ожидал, что получу хоть какой-то ответ, тем более от сотрудника Intel, тем более так быстро, и уж тем более содержащий то, о чем я просил.

Отчаившись совсем, я начал проверять все формулы и весь код буквально по буквам, параллельно расписывая на листочке всё, что происходит с данными.

И нашел опечатку, причем именно в том месте, в котором меньше всего сомневался: там где нужно вычислить я брал вместо . И эта коварная опечатка всё ломала, но не так чтобы совсем.

Мораль — семь раз проверь формулы и код, один раз пиши письмо китайским ученым.

Ну а если серьезно, надеюсь вам интересно и познавательно было читать этот рассказ. Желаю всем гореть своим делом, но не выгорать!

Список литературы

1. Ozyagcilar, T. "Calibrating an eCompass in the Presence of Hard and Soft-iron Interference."

2. Cheng Chi et al 2019 IOP Conf. Ser.: Earth Environ. Sci. 237 032015

3. Ellipsoid or sphere fitting for sensor calibration

4. K. Han, H. Han, Z. Wang and F. Xu, "Extended Kalman Filter-Based Gyroscope-Aided Magnetometer Calibration for Consumer Electronic Devices," in IEEE Sensors Journal, vol. 17, no. 1, pp. 63-71, 1 Jan.1, 2017, doi: 10.1109/JSEN.2016.2624821.

5. Li Wenkuan et al 2020 J. Phys.: Conf. Ser. 1627 012028