В прошлой статье я показал, как условие с парой однотипных неравенств, плохо поддающееся индексации с помощью btree, можно переделать на эффективно gist-индексируемое в PostgreSQL условие относительно диапазонных типов, а наш сервис анализа планов запросов explain.tensor.ru подскажет, как именно это сделать.
Но что делать, если неравенств у нас не два, а целых четыре, да еще и с разными типами участвующих полей? Например, для целей бизнеса это может быть задачей вроде "найди мне все продажи за декабрь на сумму 10-20K", что на SQL будет выглядеть примерно так:
dt >= '2023-12-01'::date AND dt <= '2023-12-31'::date AND
sum >= 10000::numeric AND sum <= 20000::numeric

Сформируем тестовые данные:
CREATE TABLE sales AS
SELECT
id
, now()::date - (random() * 1000)::integer dt
, (random() * 1e6)::numeric(32,2) sum
FROM
generate_series(1, 1e6) id;Сначала попробуем наивный подход с индексом по паре полей под условием:
CREATE INDEX ON sales(dt, sum);
EXPLAIN (ANALYZE, BUFFERS, COSTS OFF, SUMMARY OFF)
SELECT
*
FROM
sales
WHERE
dt >= '2023-12-01' AND dt <= '2023-12-31' AND
sum >= 10000::numeric AND sum <= 20000::numeric;Кажется, что все выглядит более чем пристойно - прочитали 461 страницу данных (что важно, если они не находятся в оперативном кэше, и приходится медленно и грустно читать эти 3.6MB с диска) и заняло это 5.3мс:
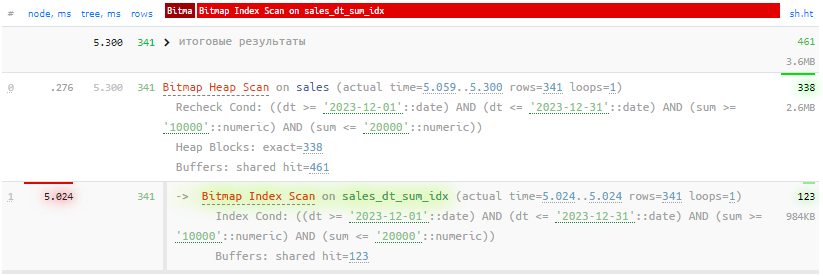
Подключаем "геометрию"
Но давайте взглянем на нашу задачу чуть под иным углом - геометрическим:
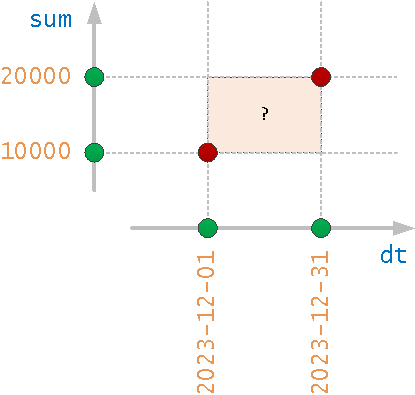
Если мы расположим столбцы dt и sum по разным координатным осям, то искомые записи будут представлены точками с координатами значений этих столбцов, а пересечение условий интервалов их значений даст нам прямоугольник, углами которого будут пары минимальных/максимальных значений искомых интервалов.
То есть задача сводится к нахождению точек, находящихся внутри прямоугольника - а это задача как раз для GiST-индекса! Единственный нюанс - тип date нам придется привести к числовому значению с помощью функции extract:
-- индексируем "точки"
CREATE INDEX ON sales USING gist(point(extract(EPOCH FROM dt), sum));Перепишем запрос, используя оператор включения (<@):
EXPLAIN (ANALYZE, BUFFERS, COSTS OFF, SUMMARY OFF)
SELECT
*
FROM
sales
WHERE
point(extract(EPOCH FROM dt), sum) <@ box( -- "точка" принадлежит прямоугольнику
point(extract(EPOCH FROM '2023-12-01'::date), 10000) -- min-угол
, point(extract(EPOCH FROM '2023-12-31'::date), 20000) -- max-угол
);В результирующем плане изменились лишь условия и используемый индекс, но читать теперь нам пришлось на 10% меньше страниц, а время выполнения запроса сократилось в 8 раз:
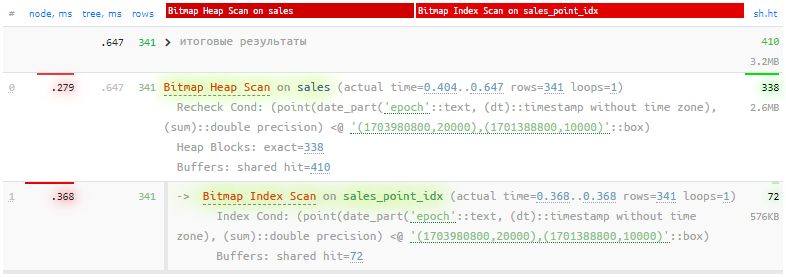
Здесь преимущество GiST-индекса заключается в возможности использования в запросе с помощью модуля btree_gist дополнительных скалярных "координат" - например, идентификатора магазина. Насколько это бывает полезно, я подробно разбирал в статье "PostgreSQL Antipatterns: работаем с отрезками в «кровавом энтерпрайзе»".
Но если такой задачи нет, мы можем воспользоваться более "геометрически-заточенным" индексом SP-GiST:
CREATE INDEX sales_point_spgist
ON sales USING spgist(
point(extract(EPOCH FROM dt), sum)
);Это позволяет уменьшить объем чтений и ровно тот же запрос ускорить еще в 1.5 раза примерно:
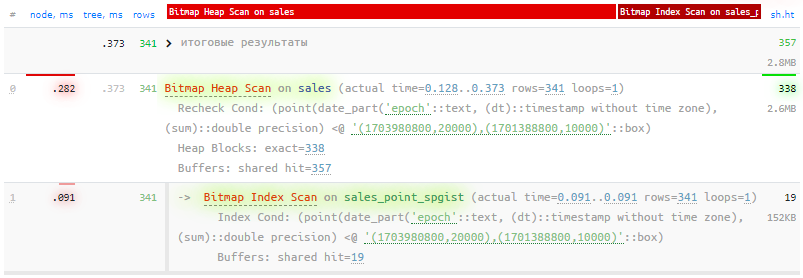
Так что если для вас разница между 5.30мс и 0.37мс вдруг окажется значима при выполнении запроса и стоит небольшого его усложнения - вспомните про возможности gist/spgist.
А еще "геометрический" поиск можно использовать для нетривиального решения задач типа префиксного FTS-поиска с релевантностью по дате.


Sap_ru
А зачем вы использовали индекс по паре знаний, а не два индекса, если у вас значения не связанные?
Kilor Автор
BitmapAndобычно стоит избегать, он почти всегда проигрывает составному индексу за редкими исключениями.https://explain.tensor.ru/archive/explain/f0d4564d9536a996688fe0b96a4a87b2:0:2024-03-15
Sap_ru
Странное говорите... У вас-то он выиграл относительно составного индекса, хоть и немного. И по моему опыту он всегда выигрывает, что очевидно. Сравнивать только время поиска, то выиграл он очень хорошо.
И по количеству прочитанных страниц он вас тоже впереди составного индекса (в полтора раза, однако!), причем, по мере роста объема базы отрыв будет нарастать. А уж если увеличить количество условий и/или индексов, то там и в разы разница будет. Нельзя так индексы использовать, это по количеству страниц при поиске видео.
И более того, по количеству страниц он на уровне примера с gist!
И теперь возникли вопросы к gist и чистоте эксперимента - количество страниц одинаковое, а время исполнения запросов отличается на порядок. Тут что-то не так. Тут совершенно точно дело не во времени поиска. Кэширование, разное хранение данных, что-то ещё разное.
Kilor Автор
Относительно составного по времени он тут выиграл 5.03 против 5.30, и 410 против 461 по страницам - то есть "копейку". Но выиграл ровно потому, что "двихдиапазонный" поиск по btree заведомо неэффективен.
А вот gist как раз выигрывает за счет более оптимизированного хранения самого дерева индекса - из heap страницы-то читались все разы одни и те же 338 за примерно 0.28-0.30мс.
Sap_ru
Я про первый вариант gist. Количество страниц индекса совпадает с их количеством в случае двух индексов, но время чтения этих страниц в 15 раз меньше. Вот это странно. Что-то тут с временами не так, а если ориентироваться только на количество страниц, то картина получается немного иной, хотя sp-gist всё равно окажется впереди. Но зато обычный gist сравняется с правильными индексами, что логично, так как чудес не бывает и никаких супер-волшебных алгоритмов там под капотом нет.
Кроме того, у вас эксперимент все равно не чистый. Тогда нужно было и с обычными (двумя!) индексами date в целое/плавающее преобразовать!
Самая страшная тайна заключается в том, что внутри себя gist использует ровно те же b-trees ровно таким же образом! По индексу на каждое изменение - всё так, как и должно быть в нормальной базе. Там нет никакой магии. И при поиске не должно быть большой разницы с обычными индексами плавающих или целых чисел. А вы почему-то исходите из того, что у gist под капотом какая-то волшебная магия.
Kilor Автор
Какая уж тут магия? Все вполне объяснимо:
gistдостаточно быстро "схлапывается" до нужного прямоугольника, где находятся только искомые точки, а вотbtree, фактически, для каждого подходящего значенияdtделает вложенный поиск интервала поsum, что явно не быстро, поскольку линейно растет с количеством уникальных подходящих значенийdtв интервале.То есть нашли мы, например, значение
dt = '2023-12-15', полезли искать внутри поsum- там ничего подходящего, а время уже потрачено.Sap_ru
Ради интереса полез в gist. Да, там должен быть заметный прирост скорости, так как поиск осуществляется сразу по двум индексам, а деревья сбалансированы.
Тем не менее результаты странные, так как при равном количестве страниц индекса скорость поиска отличается на порядок.