Разработка системы управления электроприводом постоянного тока. Часть 1

Главная
Разработка системы управления электроприводом постоянного тока. Часть 1 — математическая модель

Разработка системы управления электроприводом постоянного тока. Часть 1 — математическая модель

01.04.2024 10:40

Dileon44 14 3400 Источник

1. Вступление

Статья входит в цикл публикаций, посвящённых созданию системы управления (СУ) электроприводом рулевой поверхности (РП) малогабаритной ракеты на FPGA.

Целью данной статьи является краткое изложение процесса разработки математической модели (ММ) робототехнической системы, которая описывает как электромеханическую часть, так и алгоритм управления, реализованный в цифровом устройстве - FPGA (Altera Cyclone IV). Логика, реализованная в FPGA, будет описана в следующей части.

Краткое содержание статьи:

описание конструкции электропривода
создание ММ привода
экспериментальное определение некоторых параметров электродвигателя
анализ результатов математического моделирования

2. Техническое задание

Необходимо реализовать СУ для уже существующего привода (есть только конструкция), которая должна удовлетворять следующим требованиям по динамике, точности и устойчивости:

время переходного процесса при повороте вала привода на 30 градусов не должно превышать $t_{пп} \leq 0,2 \, сек$ ;
перерегулирование не должно превышать 15% $(\sigma \leq 15\%)$ ;
статическая ошибка не должна превышать $\theta_{рассогласования} \leq 0,1^{\circ}$ ;
частота среза $f_{ср} = 14 \pm1 \, Гц$ при амплитуде входного сигнала $\varphi_{in} = 1^{\circ}$ ;
запас по фазе на частоте среза должен быть не меньше, чем $50^{\circ} (\triangle \Psi \geq 50^{\circ})$ .

3. Описание конструкции привода

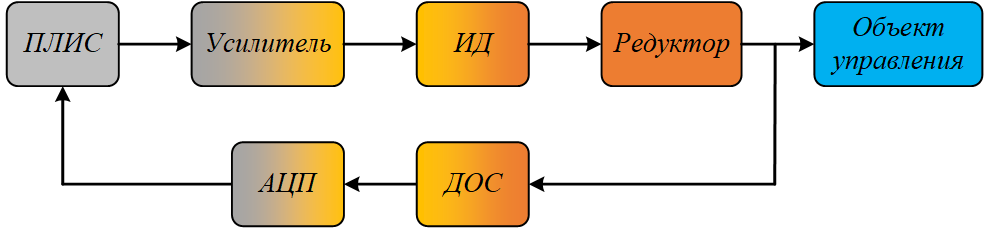
Для создания ММ необходимо понять, что из себя представляет конструкция привода. Механическая часть (рисунок 1) состоит из следующих элементов: исполнительного двигателя (ИД), в качестве которого используется коллекторный электродвигатель постоянного тока – ДПР 62-Н4-01; пятиступенчатого цилиндрического редуктора, на предпоследней ступени которого расположен потенциометрический датчик обратной связи (ДОС).

Первоначально данная конструкция входила в состав испытательного стенда, поэтому на выходной вал привода была установлена муфта для последующего присоединения датчика момента. Демонтаж этой муфты не представлялся возможным: резьба, соединяющая её с приводом посажена на клей. В этой связи в ММ будет учтен момент инерции, создаваемый муфтой.

Рисунок 1 - Внешний вид привода рулевой поверхности

В состав приводной системы входит электронный блок, который состоит из цифрового устройства управления - FPGA, усилителя (плата-драйвер для электродвигателя) и внешнего АЦП.

4. Математическая модель привода

Математическая модель состоит из:

Редуктора
Электродвигателя
Потенциометра
АЦП
Вычислительного блока
Силовой платы
Помехи потенциометра

Рисунок 3 - Математическая модель привода рулевой поверхности

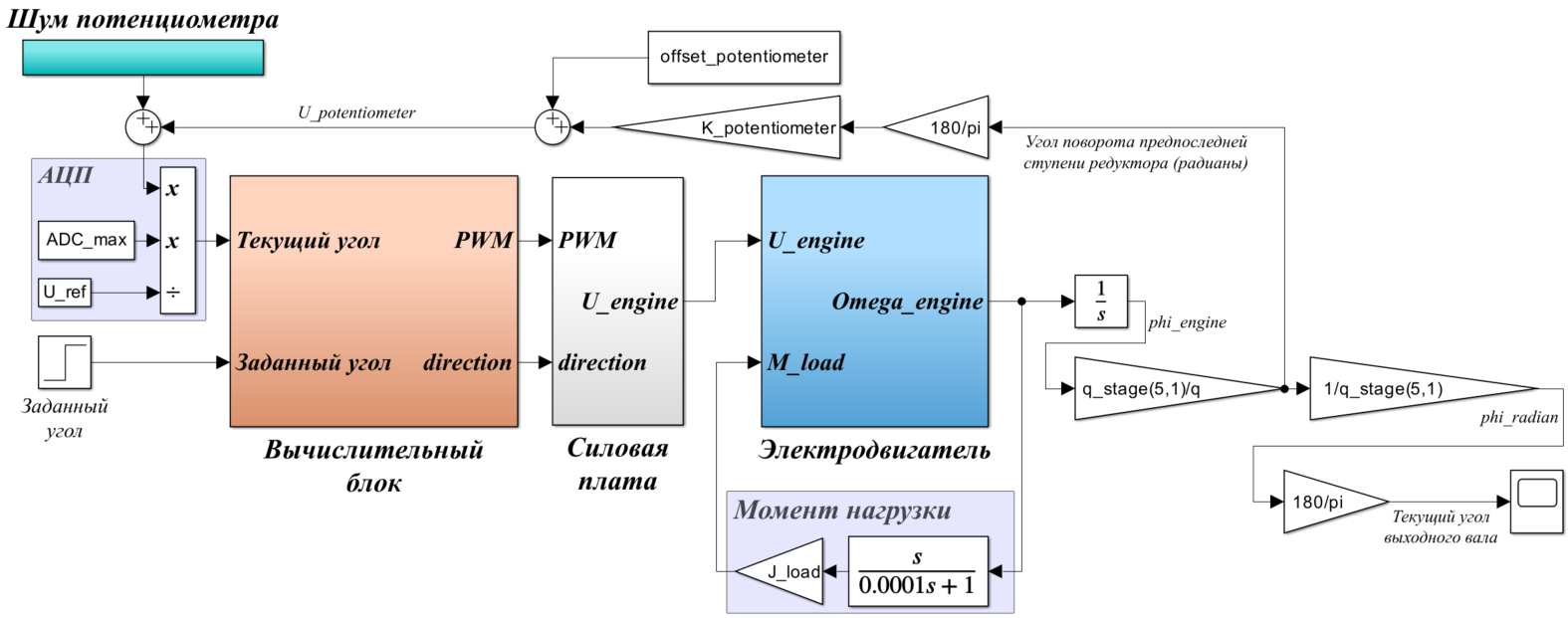
Уравнения, описывающие данную модель:

$\begin{cases} ИД - \begin{cases} u_{дв}(t)=R_{дв} \, i_{дв}(t) + L_{дв}\frac{di_{дв}(t)}{dt}+c_{e} \, \Omega_{дв}(t)\\ M_{дв}(t)=c_{м} \, i_{дв}(t) \\ J_{дв} \frac{d\Omega_{дв}(t)}{dt} = M_{дв}(t) + M_{нагр \rightarrow дв}(t) \end{cases} \\ \\ u_{пот}=K_{пот} \cdot (\varphi_{пот} \cdot \frac{180}{\pi}) \, + \, 2,5 \\ \\ ЭБП - \begin{cases} \varphi_{ADC_n}=(2^{12}-1) \cdot \frac{u_{пот}}{u_{ref}} \\ \varphi_{тек_n} = \varphi_{ADC_n} \cdot \frac{360^{\circ}}{2^{ADC_{resolution}}-1} - 180^{\circ} \\ \varphi_{фильтр_n} = \frac{1}{N}\sum^{N-1}_{k=0} \varphi_{тек_{ \, n-k}} \\ \theta_{n} = \varphi_{заданный_n} - \varphi_{текущий_n} \qquad (\varphi_{заданный_n} = \varphi_{заданный \, вых. \, вал_n} \cdot q_{5 \rightarrow 6}) \\ \theta_{PI_{\,n}} = K_P \cdot \theta_{n} + \theta_{I_{\,n-1}} + K_I \, \theta_{n} \, \triangle t \\ \end{cases} \\ \\ u_{дв}= D \cdot u_{пит} \qquad (D = \frac{\theta_{PI_n}}{316^{\circ}}) \end{cases}$

Данная ММ не учитывает:

шарнирный момент – момент нагрузки, создаваемый воздушным потоком и прикладываемый к РП. Он пропорционален углу поворота РП относительно продольной оси ракеты: чем $\uparrow$ угол, тем $\uparrow$ шарнирный момент;
момент вязкого трения – момент, который прикладывается к твёрдому телу при его движении в жидкой или газообразной среде;
момент сухого трения – момент от трения в подшипниках, трения между шестернями и т.д.;
люфт редуктора;
жёсткость редуктора.

Так как в паспортных данных двигателя отсутствуют некоторые параметры, для ММ необходимо определить:

передаточное число редуктора $(q_{ред});$
момент инерции редуктора и муфты $(J_{нагр});$
момент инерции ротора двигателя $(J_{д в});$
сопротивление обмотки двигателя $(R_{дв});$
индуктивность $(L_{дв});$
коэффициент противо-ЭДС двигателя
коэффициент момента

Момент нагрузки определяется произведением ускорения выходного вала электродвигателя на приведённый к валу двигателя момент инерции нагрузки (второй закон Ньютона для вращательного движения):

$M_{нагр}=J_{нагр} \cdot \varepsilon_{двигатель}$

Момент инерции нагрузки состоит из суммы моментов инерции редуктора, муфты и аэродинамического руля:

$J_{нагр}=J_{редуктор}+J_{муфта}+J_{руль}$

Так как испытания проводились без аэродинамического руля, его момент инерции равен нулю. Необходимо определить приведённый к валу электродвигателя момент инерции редуктора и муфты.

4. 1. Редуктор

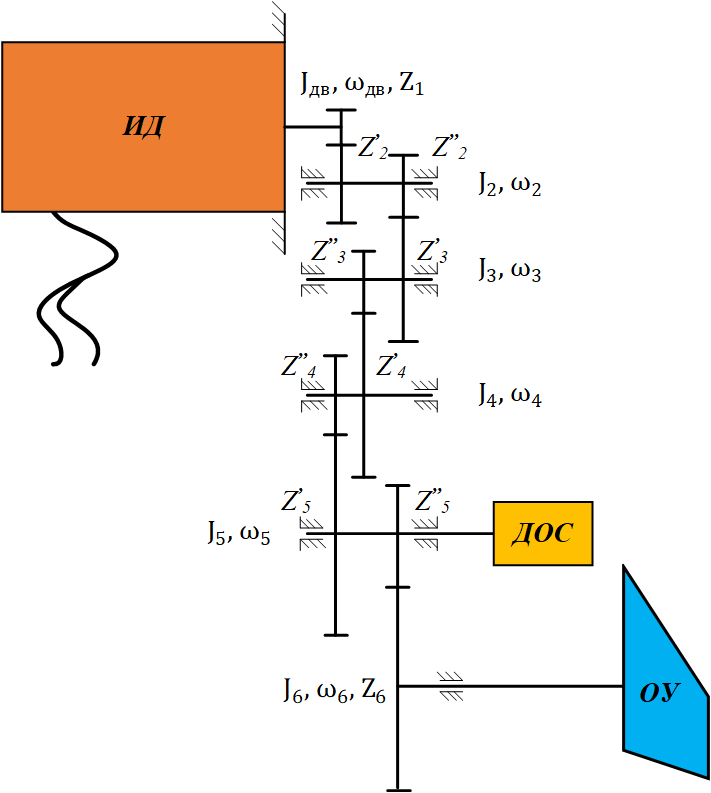
Цилиндрический пятиступенчатый редуктор на промежуточных валах (валы № 2, 3, 4, 5 на рисунке 4) имеет по две шестерни. Это сделано с целью уменьшения люфта, габаритов редуктора и достижения необходимого момента на выходном валу привода.

Определим передаточное число редуктора, а также его суммарный момент инерции.

4. 1. 1. Передаточное число редуктора

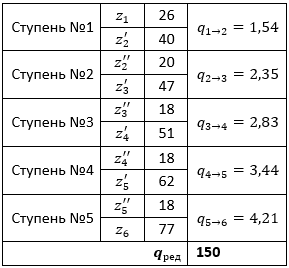
Чтобы вычислить передаточное число всего редуктора, необходимо рассчитать передаточные числа между всеми ступенями и перемножить их:

$q_{ред}=\prod^{N=5}_{i=1}q_{i \rightarrow i+1}$

Передаточное число между двумя последовательно соединёнными зубчатыми колёсами определяется соотношением:

$\qquad \qquad \qquad q_{i \rightarrow i+1}=\frac{z_{i+1}}{z_i} = \frac{\omega_{i}}{\omega_{i+1}} \qquad (1)$

где $z_i, \omega_i -$ количество зубьев и угловая скорость каждого i-ого зубчатого колеса.

Представленная конструкция редуктора позволяет определять передаточные числа визуально путём подсчёта количества зубьев каждого зубчатого колеса.

Таблица 1 - Расчёт передаточного числа редуктора

4. 1. 2. Момент инерции редуктора и муфты

Для определения момента инерции редуктора, необходимо знать моменты инерции всех валов и зубчатых колёс в нём. Конструкция и размеры элементов редуктора известны. Так как они имеют форму диска, момент инерции будем определять по известной формуле (плотность стали примем равной – $\rho=7900 \, кг \cdot м^3$ ):

$J=\frac{m \cdot R^2}{2}=\frac{\rho \cdot V \cdot R^2}{2}= \frac{\rho \cdot l \cdot \pi \cdot R^4}{2}= \frac{\rho \cdot l \cdot \pi \cdot D^4}{32}$

Рисунок 5 - Габаритный чертёж промежуточного вала редуктора

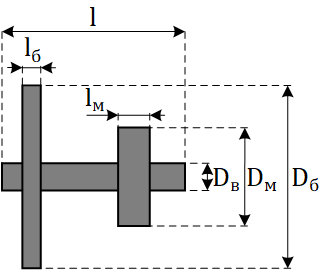
Каждый промежуточный вал в редукторе включает в себя по два зубчатых колеса (б - большое, м - маленькое). При вычислении момента инерции самого вала длина равна: .

Вычисления моментов инерции промежуточных валов редуктора и выходного вала с посаженной на него муфтой представлены в таблице №2 (все размеры приняты в миллиметрах).

Зубчатое колесо на выходном валу имеет форму сектора окружности (рисунок 6). Это даёт возможность уменьшить массу привода, а также поставить физическое ограничение хода выходного вала привода. Для упрощения вычисления момента инерции, масса этого зубчатого колеса была поделена на 5, так как она занимает сектор окружности примерно в $70^{\circ}$ .

Таблица 2 - Вычисление момента инерции элементов редуктора

Чтобы привести распределённые моменты инерции всех элементов редуктора из таблицы №2 $(J_{2}, J_{3}, J_{4}, J_{5}, J_{6})$ к одной оси вращения, необходимо электропривод свести к одномассовой системе с эквивалентным моментом инерции $J_{\sum}$ . Эквивалентная одномассовая система электропривода, имеющая момент инерции $J_{\sum}$ , вращается со скоростью электродвигателя $\omega_{дв}$ . Приведение моментов инерции к одной оси вращения производится на основании принципа сохранения кинетической энергии исходной многомассовой системы с распределенными моментами инерции (рисунок 4) и одномассовой системы с эквивалентным моментом инерции $J_{\sum}$ :

$J_{\sum}\frac{\omega^2_{дв}}{2} = J_{дв}\frac{\omega^2_{дв}}{2} + J_{2}\frac{\omega^2_{2}}{2} + J_{3}\frac{\omega^2_{3}}{2} + J_{4}\frac{\omega^2_{4}}{2} + J_{5}\frac{\omega^2_{5}}{2} + J_{6}\frac{\omega^2_{6}}{2}$

разделим правую и левую части уравнения на $\frac{\omega^2_{дв}}{2}$ , получим

$J_{\sum} = J_{дв} + J_{2}\frac{\omega^2_{2}}{\omega^2_{дв}} + J_{3}\frac{\omega^2_{3}}{\omega^2_{дв}} + J_{4}\frac{\omega^2_{4}}{\omega^2_{дв}} + J_{5}\frac{\omega^2_{5}}{\omega^2_{дв}} + J_{6}\frac{\omega^2_{6}}{\omega^2_{дв}}$

С учётом (1) и рассчитанными значениями передаточных чисел между каждой ступенью редуктора (таблица 1) получим:

$J_{\sum} = J_{дв} + \frac{J_{2}}{q^2_{1 \rightarrow 2}} + \frac{J_{3}}{(q_{1 \rightarrow 2}q_{2 \rightarrow 3})^2} + \frac{J_{4}}{(q_{1 \rightarrow 2}q_{2 \rightarrow 3}q_{3 \rightarrow 4})^2} + \\ + \frac{J_{5}}{(q_{1 \rightarrow 2}q_{2 \rightarrow 3}q_{3 \rightarrow 4}q_{4 \rightarrow 5})^2} + \frac{J_{6}}{q^2_{ред}} \qquad (2)$

Момент инерции нагрузки $J_{нагр}$ , который состоит из момента инерции редуктора и муфты, прикреплённой к выходному валу, равен суммарному моменту инерции $(J_{\sum})$ за вычетом момента инерции двигателя $(J_{дв})$ :

$J_{нагр} = \frac{J_{2}}{q^2_{1 \rightarrow 2}} + \frac{J_{3}}{(q_{1 \rightarrow 2}q_{2 \rightarrow 3})^2} + \frac{J_{4}}{(q_{1 \rightarrow 2}q_{2 \rightarrow 3}q_{3 \rightarrow 4})^2} + \frac{J_{5}}{(q_{1 \rightarrow 2}q_{2 \rightarrow 3}q_{3 \rightarrow 4}q_{4 \rightarrow 5})^2} + \frac{J_{6}}{q^2_{ред}} = \\ =3,06 \cdot 10^{-8} кг \cdot м^2$

Таким образом, для ММ определены передаточное число редуктора $q_{ред }=150$ и момент инерции нагрузки $J_{нагр}=3,06 \cdot 10^{-8} кг \cdot м^2$ . На практике слагаемыми, которые относятся к моментам инерции промежуточных шестерён редуктора (в уравнении (2) ), пренебрегают, так как их величины малы по сравнению с моментом инерции объекта управления (например, аэродинамический руль).

4. 2. Электродвигатель

Динамика двигателя постоянного тока (ДПТ) описывается известной системой уравнений:

$\qquad \qquad \qquad \begin{cases} u_{дв}(t)=R_{дв} \, i_{дв}(t) + L_{дв}\frac{di_{дв}(t)}{dt}+c_{e} \, \Omega_{дв}(t) \qquad (3)\\ M_{дв}(t)=c_{м} \, i_{дв}(t) \\ J_{дв} \frac{d\Omega_{дв}(t)}{dt} = M_{дв}(t) + M_{нагр \rightarrow дв}(t) \end{cases}$

где $\Omega_{дв} [рад/с]-$ угловая скорость ротора относительно статора, $M_{дв} [Н \cdot м] -$ электромеханический момент, $M_{нагр \rightarrow дв} [Н \cdot м] -$ момент нагрузки, передаваемый со стороны редуктора (момент нагрузки, приведённый к валу двигателя). Применим к системе уравнений преобразование Лапласа:

$\qquad \qquad \begin{cases} u_{дв}(s)=R_{дв} \, i_{дв}(s) + L_{дв}i_{дв}(s) \cdot s + c_{e} \, \Omega_{дв}(s) \\ M_{дв}(s)=c_{м} \, i_{дв}(s) \\ J_{дв} \Omega_{дв}(s) \cdot s = M_{дв}(s) + M_{нагр \rightarrow дв}(s) \end{cases}$

Преобразуем

$\begin{cases} i_{дв}(s)=[u_{}(s)-c_{e}\Omega_{дв}(s)] \cdot \frac{1/R_{дв}}{T_{я} \cdot s + 1} \\ M_{дв}(s)=c_{м} \, i_{дв}(s) \\ \Omega_{дв}(s) = \frac{M_{дв}(s) + M_{нагр \rightarrow дв}(s)}{J_{дв} \cdot s} \end{cases}$

где $T_{я}=L_{дв}/R_{дв}-$ электрическая постоянная времени якоря. Из полученной системы построим структурную схему в Simulink.

Рисунок 7 - Структурная схема электродвигателя

Для ММ следует определить такие параметры, как: сопротивление обмотки двигателя $R_{дв}$ , индуктивность обмотки $L_{дв}$ , момент инерции ротора $J_{дв}$ , коэффициент противо-ЭДС $c_{e}$ и коэффициент момента $c_{m}$ , так как в паспортных данных они отсутствуют.

4. 2. 1. Сопротивление

Сопротивление обмотки якоря двигателя было измерено мультиметром:

$R_{дв}=3.1 \, Ом$

4. 2. 2. Индуктивность

Индуктивность обмотки рассчитана по формуле:

$L_{дв}=k_1 \frac{U_{ном}}{2 \, p \, n_{ном} \, I_{ном}}=8 \cdot \frac{27}{2 \cdot 2 \cdot 6000 \cdot 1}=0.009 \, Гн$

где для быстроходных машин, для нормальных некомпенсированных машин, для компенсированных машин. Примем .

4. 2. 3. Момент инерции

Момент инерции ротора выбран по подобным двигателям, исходя из массо-габаритных характеристик: $J_{дв}=2,5 \cdot 10^{-6} \, кг \cdot м^2$

4. 2. 4. Коэффициент противо-ЭДС

Коэффициент противо-ЭДС определён экспериментально по формуле:

$c_{e}=\frac{u_{дв}-R_{дв}\,i_{дв}}{\Omega_{дв}} \qquad \left[\frac{В \cdot с}{рад}\right]$

Данная формула получается из уравнения (3) в установившемся режиме.

Эксперимент состоит в следующем:

датчик положения ротора (в данном случае потенциометр) через своеобразную муфту крепится к выходному валу двигателя так, как показано на рисунке 8.

Рисунок 8 - Соединение потенциометра с ротором двигателя
на двигатель подаётся напряжение $u_{ дв}$ ;
мультиметром измеряется ток в установившемся режиме;
зная время полного оборота потенциометра (данные с него передаются на ПК), определяется скорость вращения двигателя по формуле $\Omega_{дв}=2\pi/\triangle t_{об}$ [рад/с]. На рисунке 9 показаны данные, считанные с потенциометра и переданные на ПК.

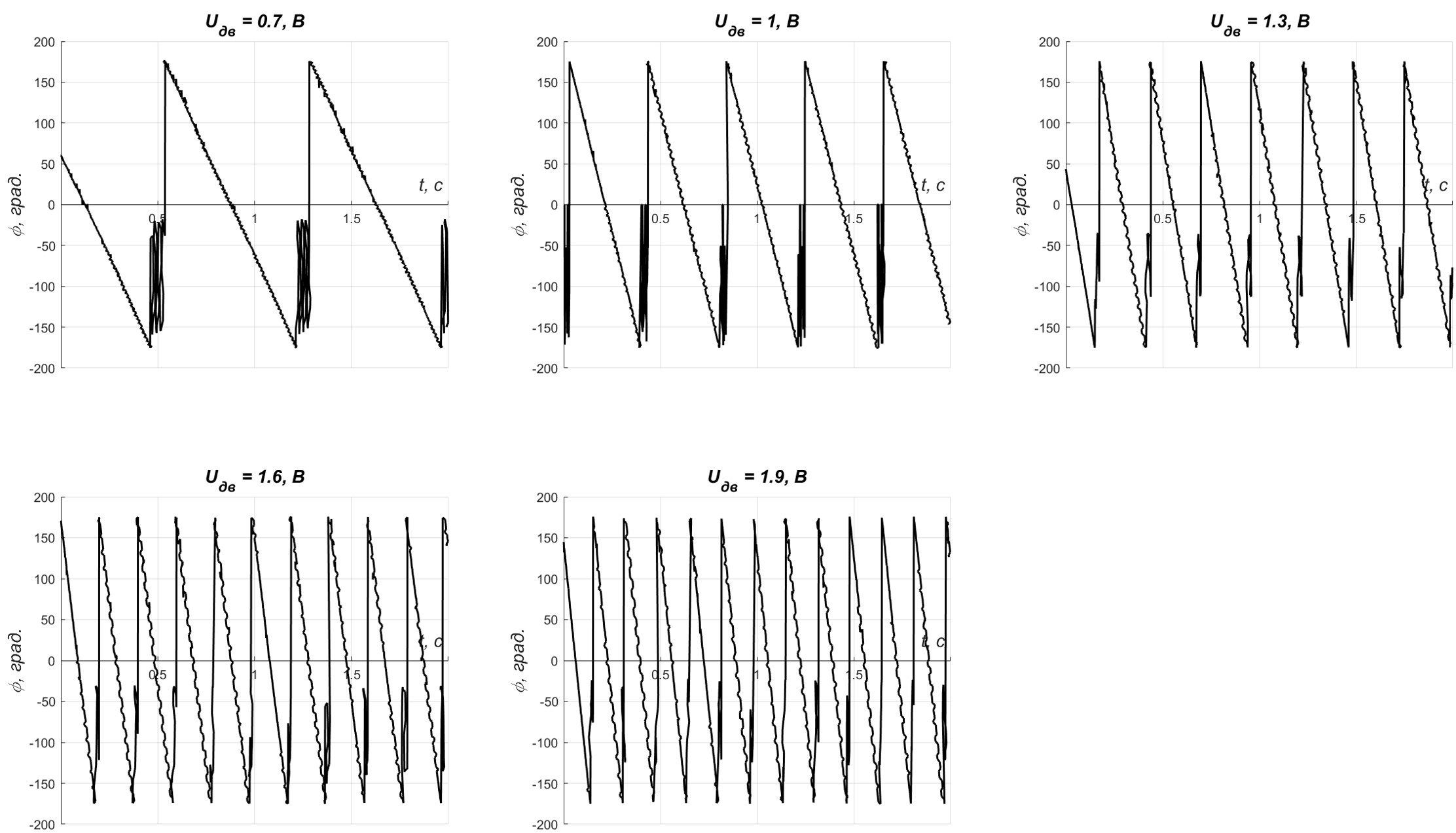
Рисунок 9 - Зависимости угла поворота ротора от времени при разных напряжениях двигателя
определяется коэффициент противо-ЭДС по формуле:

$c_{e}=(u_{дв}-3,1 \cdot i_{дв}) \, \frac{\triangle t_{об}}{2\pi}$

меняется напряжение $u_{дв}$ и повторяются пункты 3 - 5.

Все вычисления сведены в таблицу 3:

Таблица 3 - Экспериментальные данные для определения коэффициента противо-ЭДС

Рисунок 10 - Зависимость коэффициента противо-ЭДС от напряжения двигателя

Рисунок 11 - Регулировочная характеристики двигателя

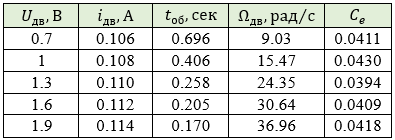
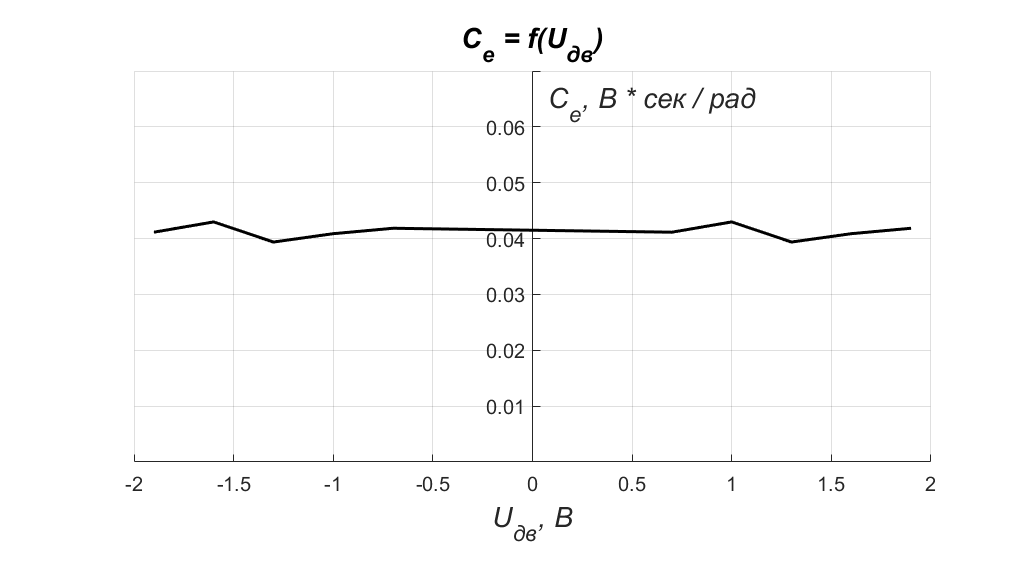
Таким образом, среднее значение коэффициента противо-ЭДС $c_{e}=0,041 \, [В \cdot с/рад]$ .

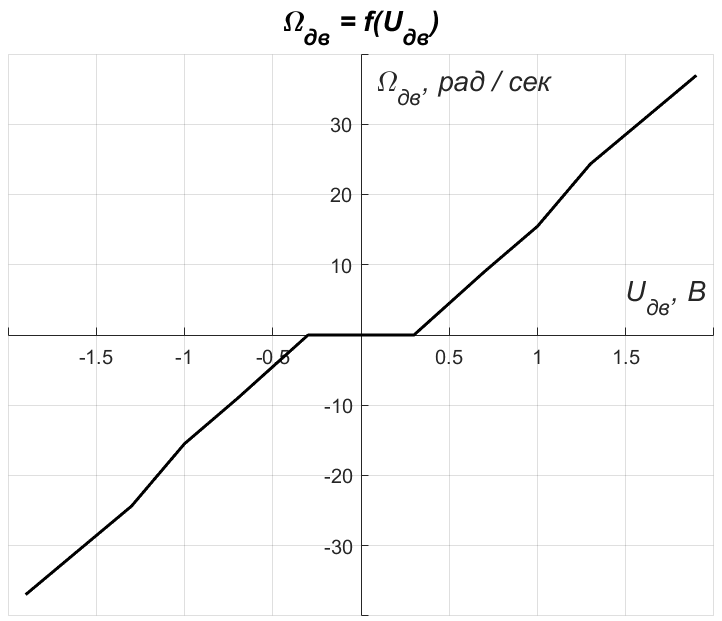
При отрицательных напряжениях двигателя (вращение в другую сторону) данные будут идентичные. Построим регулировочную характеристику электродвигателя (рисунок 11).

Стоит отметить, что при малых напряжениях ротор двигателя вращаться не будет, так как всё напряжение падает на активном сопротивлении обмотки (появляется нелинейность в виде зоны нечувствительности). Ток в цепи очень мал и, следовательно, создаётся момент, недостаточный для преодоления сил трения в подшипниках и тд.

4. 2. 5. Коэффициент момента

Коэффициент момента определяется по формуле:

$c_м=\frac{M_п}{I_п} \quad \left[\frac{Н \cdot м}{А}\right]$

Однако в паспортных данных отсутствует пусковой ток. В двигателях постоянного тока обычно принимают коэффициент момента равным коэффициенту противо-ЭДС (доказано экспериментально), поэтому $c_м=c_e=0,041 \, [Н \cdot м/А]$ .

4. 3. Потенциометр

Рисунок 12 - Габаритный чертёж СП5-21Б-1

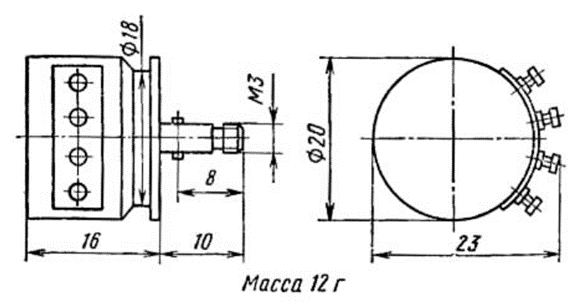
Потенциометр СП5-21Б-1 является многооборотным. Значит он преобразует входной угол $\varphi_{вх} \in [0^{\circ}; \, 360^{\circ}]$ в напряжение $u_{пот} \in [0; \, 5] \, В$ , где нулевому угловому положению соответствует нуль вольт напряжения.

Потенциометр расположен на предпоследней ступени редуктора (рисунок 4), поэтому зависимость поворота вала потенциометра от поворота выходного вала привода имеет вид:

$\varphi_{пот} = q_{5 \rightarrow 6} \cdot \varphi_{вых}$

Выходной вал привода поворачивается на $\pm \, 37,5^{\circ}$ , следовательно, максимальные углы поворота потенциометра:

$\varphi_{пот \, max} = 4,21 \cdot (\pm37,5) \approx \pm 158^{\circ}$

Следует физически расположить потенциометр так, чтобы нулю градусам поворота выходного вала привода соответствовало $u_{пот}=2,5 \, В$ , по двум причинам:

для исключения скачков напряжения от 0 В до 5 В при переходах вала потенциометра по наименьшему расстоянию от минимального сопротивления к максимальному и наоборот (движение от одной чёрной точки к другой на рисунке 13);

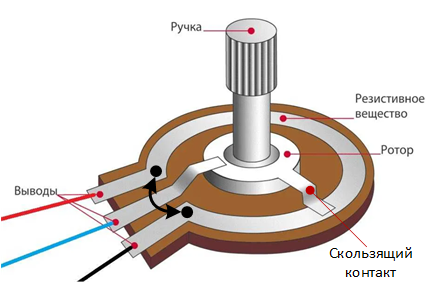
Рисунок 13 - Внутреннее устройство потенциометра
потенциометр совершает меньше одного оборота $(316^{\circ})$ при повороте выходного вала привода из минимального в максимальное положение.

Тогда формула для потенциометра примет вид:

$u_{пот}=K_{пот} \cdot \varphi_{пот} \, + \, 2,5$

где $K_{пот}=5 \, В \, / \, 360^{\circ} = 0,0139 \, [В \, / \, град]$

Также необходимо $\varphi_{пот}$ перевести из радианной меры в градусную:

$u_{пот}=K_{пот} \cdot \left( \varphi_{пот} \cdot \frac{180}{\pi} \right) \, + \, 2,5$

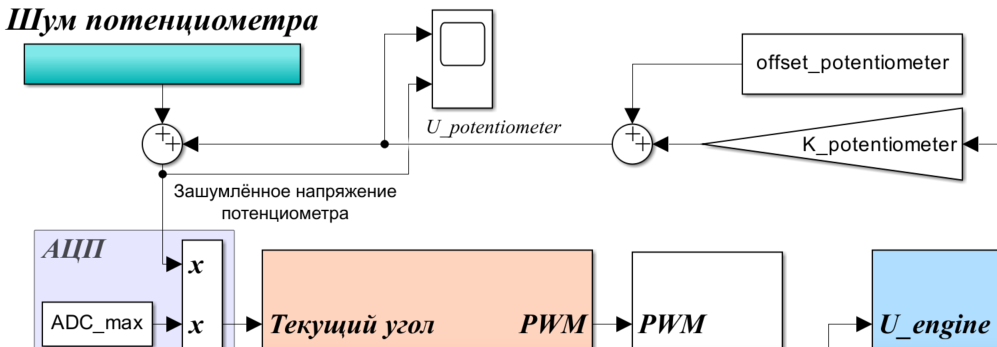
4. 4. Аналого-цифровой преобразователь

АЦП преобразует аналоговый сигнал в цифровой. MCP3201 имеет разрядность 12 бит, поэтому он имеет $2^{12}=4096$ уровней квантования и описывается соотношением:

$\varphi_{ADC}=(2^{12}-1) \cdot \frac{u_{пот}}{u_{ref}} \qquad (\varphi_{ADC} \in [0; \, 4095])$

где $u_{ref}-$ опорное напряжение, которое задаёт диапазон оцифровываемых значений. В нашем случае $u_{ref}=5 \, В$ . Например, для нейтрального положения выходного вала привода $(u_{пот}=2,5 \, В)$ АЦП будет выдавать: $\varphi_{ADC}=2048$ .

4. 5. Вычислительный блок

Оцифрованные данные поступают в цифровое устройство (в нашем случае FPGA), в котором происходят такие ключевые действия, как:

фильтрация данных с потенциометра;
вычисление угла рассогласования между требуемым углом поворота привода и текущим;
корректировка сигнала рассогласования при помощи ПИ-регулятора;
формирование широтно-импульсного сигнала (ШИС) и вычисление сигнала направления вращения электродвигателя.

Рисунок 14 - Структурная схема вычислительного блока привода

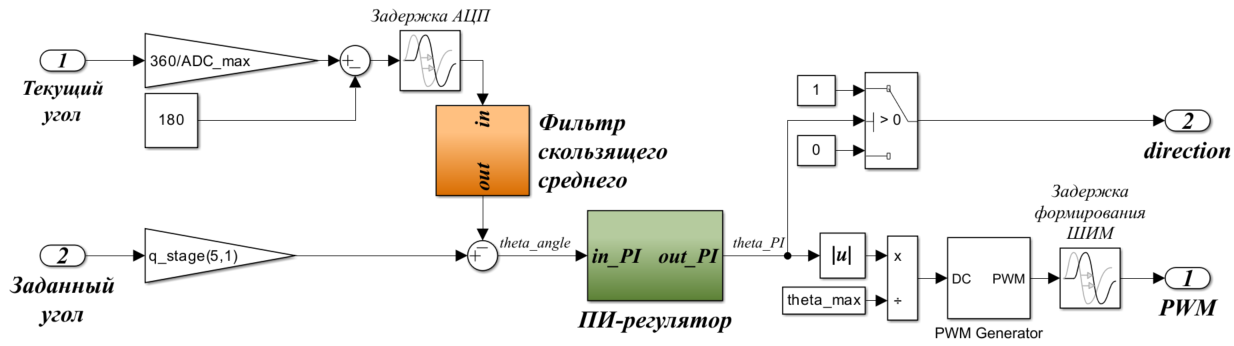
В модели вычислительного блока учтены задержка обработки данных с АЦП и задержка формирования ШИМ сигнала $(10 \, мкс)$ . Задержка АЦП равна $20 \, мкс-$ период между выборками. Задержки определены при помощи HDL-моделирования по временным диаграммам (во время разработки алгоритма под FPGA для просмотра временных диаграмм сигналов использовалась программа GTKWave).

Перед фильтрацией оцифрованные данные с АЦП переводятся в знаковый вид:

$\varphi_{тек_n} = \varphi_{ADC_n} \cdot \frac{360^{\circ}}{2^{ADC_{resolution}}-1} - 180^{\circ}$

где $\varphi_{тек_n} \in[-180^{\circ}; \, +180^{\circ}]-$ текущий угол поворота вала потенциометра в градусах. Индекс n говорит о том, что система цифровая.

4. 5. 1. Цифровой фильтр

Фильтрация данных с потенциометра происходит с помощью фильтра скользящего среднего. Он представляет собой сглаживающий фильтр с конечной импульсной характеристикой, который часто используется для сглаживания сигнала от кратковременных выбросов. Фильтрация скользящим средним выбрана по двум причинам:

простота программной реализации;
линейная фазо-частотная характеристика (постоянство времени запаздывания во всей полосе частот входных сигналов, время запаздывания зависит только от ширина окна).

В модели данный фильтр описывается соотношением:

$\varphi_{фильтр_n} = \frac{1}{N}\sum^{N-1}_{k=0} \varphi_{тек_{ \, n-k}}$

где $\varphi_{фильтр_n} \, [град] -$ отфильтрованный сигнал, ширина окна фильтрации (количество отсчётов или количество предыдущих значений угла, участвующих в фильтрации). В нашем случае (почему выбрано именно такое значение, будет объяснено в следующей статье).

Период дискретизации фильтра, время обновления входного в фильтр значения, в математической модели выбрано, исходя из периода дискретизации АЦП: $T_{д_{\, фильтр}}=T_{д_{\,АЦП}}=20 \, мкс$ .

Фильтр с каждым новым отсчётом:

запоминает текущее значение и параллельно сдвигает предыдущие значение в следующие регистры памяти;
параллельно вычисляет сумму всехзначений на каждом такте моделирования;
делит сумму на ширину окна $(\text{width_window = N = 32})$ .

Рисунок 15 - Структурная схема фильтра скользящим средним

Каждый "массив памяти" представляет собой последовательно соединённые блоки задержки и блоки сумматоров:

Рисунок 16 - Структурная схема массива памяти фильтра

Степень блока задержки указывает на то, что блок обновляет значение каждые $T=20 \cdot 10^{-6} \, сек$ , где множитель $10^{-6}-$ шаг моделирования в Simulink.

4. 5. 2. Вычисление угла рассогласования

Привод управляется по углу. Система управления работает по ошибке. Отфильтрованное значение текущего угла вычитается из требуемого угла поворота привода. Требуемый угол задаётся надсистемой (в нашем случае это блок управления ракетой).

$\theta_{n} = \varphi_{заданный_n} - \varphi_{текущий_n} \qquad \theta_n \in [-316^{\circ}; \, +316^{\circ}]$

Подразумевается, что $\varphi_{текущий_n}-$ это уже отфильтрованное значение угла поворота потенциометра, $\varphi_{заданный_n}-$ требуемое значение, приведённое к диапазону углов потенциометра:

$\varphi_{заданный_n} = \varphi_{заданный \, вых. \, вал_n} \cdot q_{5 \rightarrow 6} \\ (\varphi_{заданный_n} \in[-158^{\circ}; \, +158^{\circ}], \quad \varphi_{заданный \, вых. \, вал_n} \in[-37,5^{\circ}; \, +37,5^{\circ}])$

4. 5. 3. ПИ-регулятор

Чтобы оптимизировать переходный процесс, увеличить быстродействие, а также точность системы применяются регуляторы, которые корректируют определённым образом полученный сигнал рассогласования. В программной реализации наиболее простым регулятором является ПИ-регулятор, он описывается соотношением:

$y(t)=K_{p} \cdot x(t)+K _i \cdot \int x(t) \,dt$

Но это уравнение справедливо для непрерывных функций - аналоговых систем. Существует несколько реализаций цифровых ПИ-регуляторов [3], одна из них описывается системой уравнений:

$\begin{cases} \theta_{PI_{\,n}} = K_P \cdot \theta_{n} + \theta_{I_{\,n}} \\ \theta_{I_{\,n}} = \theta_{I_{\,n-1}} + K_I \, \theta_{n} \, \triangle t \end{cases}$

где $K_p \text{ и } K_i-$ коэффициенты пропорциональной и интегральной составляющих регулятора соответственно, $\theta_{i_{\,n}}-$ интегральная составляющая, $\theta_{PI_{\, n}}-$ выходное, отрегулированное значение угла рассогласования.

Рисунок 17 - Структурная схема цифрового ПИ-регулятора

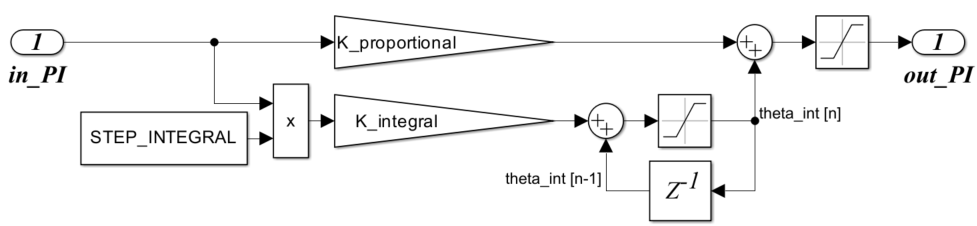
Шаг интегрирования $\triangle t= \text{STEP_INTEGRAL} = 0,008$ . Это связано с форматом слова данных в программной реализации на FPGA. При вычислениях используется формат числа с фиксированной точкой. Всего в слове данных 16 бит, из них: 1 бит под знак, 8 бит под целую часть (так как это минимальное количество бит, позволяющее вместить весь диапазон отклонения вала потенциометра: $2^{8} >158^{\circ}$ ), 7 бит под фиксированную часть. Минимальное число, которое можно представить при таком формате, в десятичной системе счисления:

$16'h0001(\text{шестнадцатеричная система счисления}) \approx 0.008$

Однако, этот показатель можно улучшить, в месте умножения увеличить ширину фиксированной части умножаемых чисел.

Выходное значение ПИ-регулятора имеет ограничение $\pm \, 316^{\circ}$ . Интегральная составляющая также ограничена. Коэффициенты $K_{p}$ и $K_{i}$ в процессе отладки варьировались, но окончательно в математической модели приняли значения: $K_{p}=33, \, K_i = 0$ .

4. 5. 4. ШИМ сигнал и сигнал направления вращения двигателя

Получен усиленный сигнал рассогласования угла $\theta_{PI}$ . В зависимости от его знака и величины формируется два сигнала: широтно-импульсный сигнал (ШИС) и сигнал направления вращения.

Рисунок 18 - Схема регулирования напряжения двигателя при помощи сигнала ШИМ

Рисунок 18 - Схема регулирования напряжения двигателя — Рисунок 19 - ШИМ-сигнал, соответствующий коэффициенту заполнения 50%

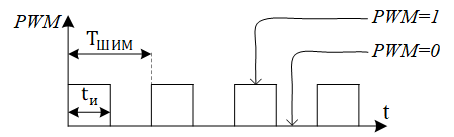
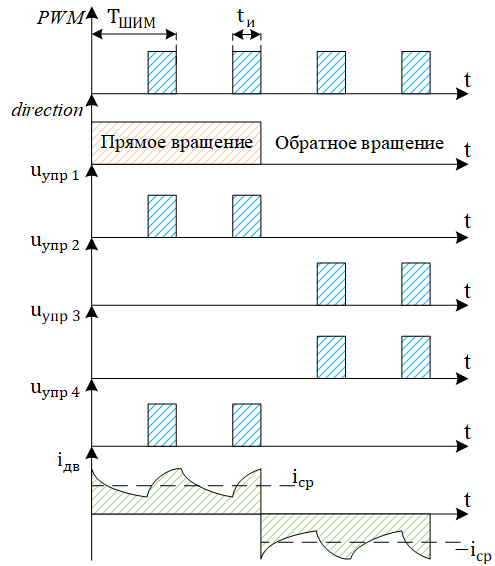
ШИС (в мат. модели это сигнал) реализует управление мощностью, подводимой к электродвигателю, при помощи изменения среднего значения напряжения на двигателе. Управление напряжением происходит посредством коммутации ключевого элемента (КЭ) определённым образом (рисунок 18). А именно, если на протяжении некоторого периода времени $T_{шим}$ (период ШИМ) транзистор будет открыт , например, 50% от этого времени $(t _и=T_{шим}/2)$ , то на двигателе сформируется среднее напряжение, равное половине напряжения питания $u_{дв}=u_{пит}/2$ . Управляющее напряжение $(u_{упр})$ , которое отвечает за открытие и закрытие КЭ, определяется ШИС (рисунок 19): если ШИСв цифровом виде равен логической единице, то $u_{упр}$ соответствует напряжению, переводящему КЭ в открытое состояние – течёт ток, иначе, если, то $u_{упр}=0 \, В$ . Таким образом, напряжение на двигателе описывается следующим соотношением:

$u_{дв}= D \cdot u_{пит}=\frac{1}{\gamma} \cdot u_{пит} \\ \left(D= \frac{1}{\gamma} = \frac{t_и}{T_{шим}}, \,D \in [0; \, 1], \, \gamma \in[1; +\infty) \, \right)$

где коэффициент заполнения ШИС, $\gamma -$ скважность ШИС.

Но где же связь между углом рассогласования и напряжением двигателя? Очевидно, что тайна кроется в коэффициенте заполнения ШИС. Если рассогласование угла максимально $(316^{\circ})$ , то и к двигателю должно прикладываться максимальное напряжение $- u_{пит}$ . И наоборот, если $\theta_{PI}=0^{\circ}$ , то $u_{дв} = 0 \, В$ . Значит можно выразить отношение угла рассогласования и напряжения на двигателе следующим образом:

$u_{дв} = \frac{\theta_{PI}}{316^{\circ}} \cdot u_{пит} \quad \left(D= \frac{\theta_{PI}}{316^{\circ}}\right) \qquad (4)$

Ошибки студента

Далее будут рассуждения, которые также вошли в текущую математическую модель, но по сути, как оказалось из вычислений, они излишне и бессмысленны. Результаты модели не поменяются, если убрать эту часть.

Потенциометр обладает чувствительностью, так как его щуп при повороте совершает перемещение от одного витка резистивного вещества к другому (отрывается от поверхности одного витка и примыкает к другому). Это приводит к тому, что сопротивление и соответственно напряжение изменяются скачкообразно. В документации к потенциометру есть параметр электрической разрешающей способности: $\lambda = 0,14-0,48\, [\, \%\, ]$ , по которому можно определить шаг изменения сопротивления при переходе от одного витка к другому. Примем среднее значение этого параметра $\lambda = 0,31 \, \%$ и определим шаг:

$\triangle R_{пот} = 6,8 \, кОм \, \cdot \, 0,31\% = 21,08 \, Ом$

Значит за один оборот мы совершаем $6800/21,08 \approx 322$ перехода между витками. Определим минимальный угол поворота, который потенциометр будет способен зафиксировать:

$\triangle \varphi_{пот \, min} = \frac{360^{\circ}}{322} = 1,12^{\circ}$

Минимальное изменение угла рассогласования такое же (можно проверить, подставив в формулы АЦП и т. д.), тогда шаг напряжения двигателя составит:

$\triangle u_{дв \, min} = \frac{\triangle\theta_{PI \, min}}{316^{\circ}} \cdot u_{пит} = \frac{1,12^{\circ}}{316^{\circ}} \cdot u_{пит} =\frac{1}{282} \cdot 27 = 0,096 \, В$

где $\frac{1}{282} = D_{min} -$ шаг коэффициента заполнения. Теперь угол рассогласования преобразуется в коэффициент заполнения следующим образом:

$D = \frac{\frac{282}{316^{\circ}} \cdot \theta_{PI}}{282}$

В данной формуле можно сократить 282 и снова получится формула (4), поэтому эти действия были бессмысленны и, видимо, коэффициент заполнения не зависит от точности датчика. Главное - это соотношение текущего угла ко всему диапазону принимаемых углов.

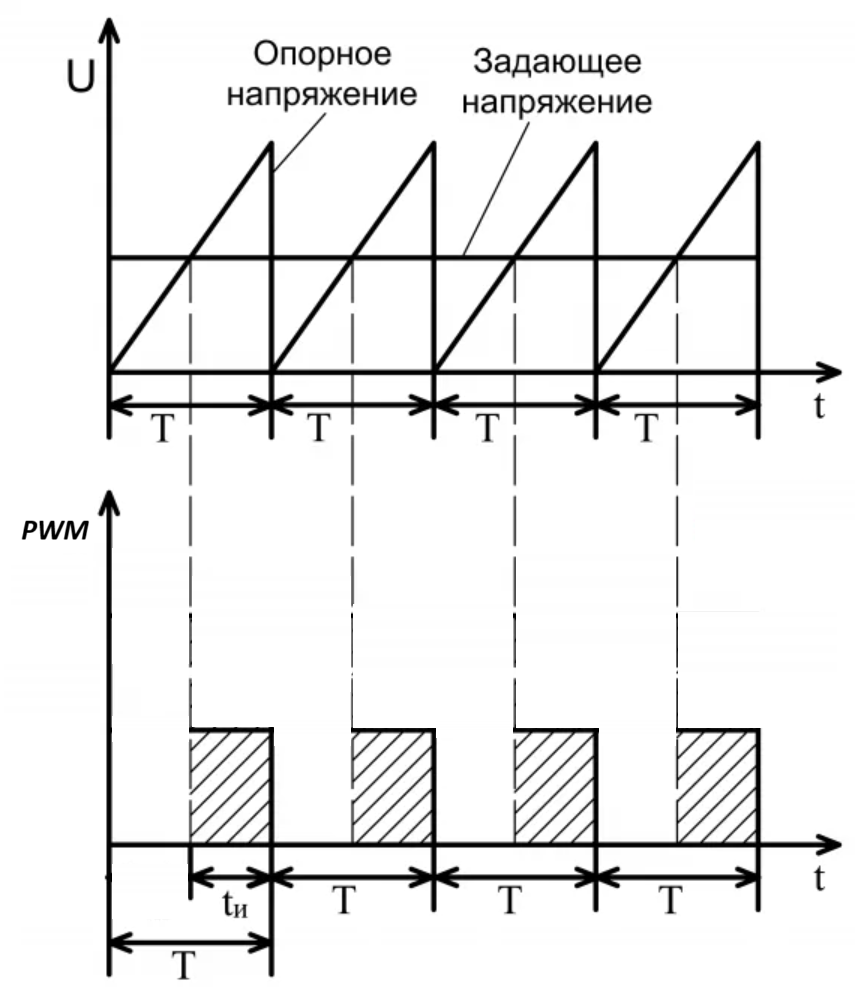
Было принято решение не убирать из модели данную часть, так как в ПЛИС уже реализован именно этот алгоритм: сначала угол переводится в размерность счётчика $(\theta_{PI} \cdot282/316)$ , который отвечает за формирование опорного напряжения (рисунок 20), а потом выполняется сравнение полученного числа со значением счётчика и формируется ШИС. Рисунок для аналоговой системы, но суть такая же: цифровой счётчик считает до значения 282 и обнуляется, параллельно его значение сравнивается с текущим значением переведённого в размерность счётчика угла рассогласования (задающее напряжение).

Ещё следует определиться с периодом ШИМ. Во-первых, он должен быть хотя бы на порядок меньше, чем электрическая постоянная времени электродвигателя $(T_{якоря})$ , чтобы двигатель не успевал реагировать на скачки напряжения (тока) и отрабатывал только среднее значение напряжения. Иными словами, электрическая постоянная времени двигателя определяет частоту входного гармонического напряжения, после которой двигатель отрабатывает этот сигнал с некоторой просадкой по мощности. Поэтому, если период ШИС будет минимум на порядок меньше, то просадка по мощности будет значительной. Двигатель будет нечувствителен (или мало чувствителен) к таким резким скачкам входного напряжения.

$T_{я} = \frac{0,009 \, Гн}{3,1 \, Ом} = 0,0029 \, c = 2,9 \, мс$

Тогда $T_{шим} \ll 2,9 \, мс \rightarrow T_{шим} \leq 0,29 \, мс$ .

Во-вторых, транзисторы в силовой плате издают свистящие звуки, если частота ШИМ находится в пределах слышимых человеком частот: до $\, 20 \, кГц \, (0,05 \, мс)$ . Поэтому пусть период ШИМ:

$T_{шим} = 50 \, мкс$

Сигнал направления вращения электродвигателя определяется знаком угла рассогласования:

$direction = \begin{cases} 1, \, если \, \theta_{PI} > 0 \\ 0, \, если \, \theta_{PI} \leq 0 \end{cases}$

4. 6. Силовая плата

Блок силовой платы имеет два входных сигнала – ШИС и направление вращения, на основе которых формируется выходной сигнал напряжения $u_{дв}$ .

Силовая плата выполняет две функции:

изменяет направление вращения двигателя, коммутируя ключевые элементы определённым образом;
усиливает напряжение, подводимое к электродвигателю.

В эксперименте в качестве силовой платы использовался модуль драйвера управления двигателями Dual 15A H-Bridge DC Motor Driver 30A 3-36V (рисунок 21).

Рисунок 21 - Внешний вид платы Dual 15A H-Bridge DC Motor Driver

Данный драйвер рассчитан на подключение двух двигателей постоянного тока. Подразумевалось, что в проекте в будущем будет реализован алгоритм управления для второго привода, который должен будет имитировать нагрузку для исследуемого привода рулевой поверхности.

Рисунок 22 - Принципиальная схема драйвера

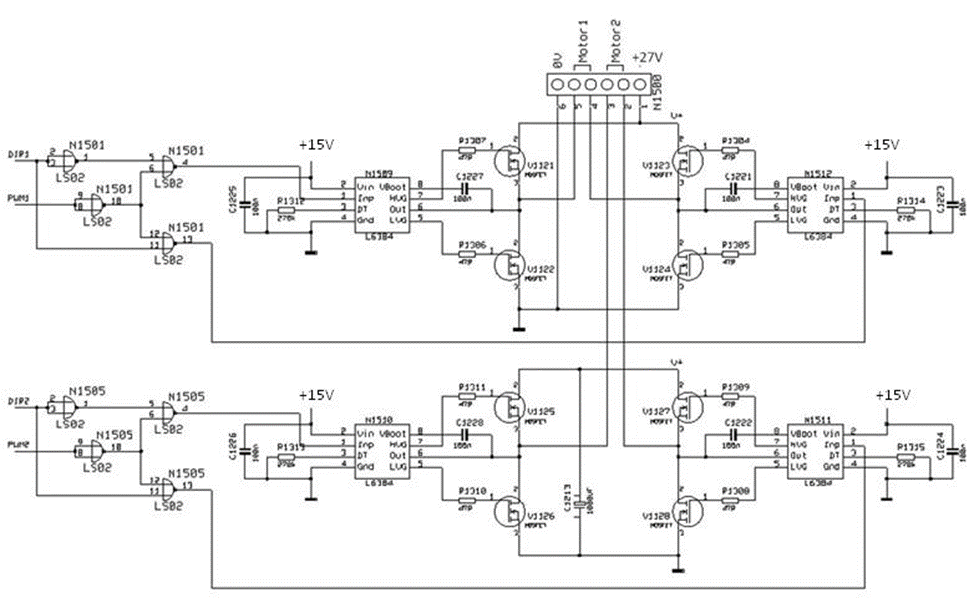
Из принципиальной схемы видно, что в драйвере используется мостовая схема. Такая схема даёт возможность изменять полярность напряжения, подводимого к двигателю, и, как следствие, направление вращения двигателя. Какой именно метод коммутации КЭ реализован в алгоритме управления платой – сказать сложно, в документации данной информации не было. Можно предположить, что используется диагональный метод коммутации КЭ (рисунки 23 и 24), так как он наиболее безопасный (отсутствуют сквозные токи) и простой в реализации. При вращении в прямом направлениикоммутируются КЭ 1 и КЭ 4 $(u_{упр \, 1} \, и \, u_{упр \, 4})$ . Когда, открыты ключи 1 и 4, двигатель находится в двигательном режиме работы (рисунок 23, а-б). Когда, все ключи закрыты, двигатель находится в генераторном режиме (рекуперация энергии в сеть) (рисунок 23, в-г).

Рисунок 23 - Пути протекания токов при коммутациях КЭ в прямом и обратном направлениях вращения (а - прямое вращение, б - обратное вращение, в - режим рекуперации энергии в сеть при прямом вращении, г - режим рекуперации энергии в сеть при обратном вращении)

Рисунок 24 - Диаграмма состояний управляющих напряжений в зависимости от ШИС и направления вращения при коэффициенте заполнения D = 0,33 (33%) — Рисунок 24 - Диаграмма состояний управляющих напряжений в зависимости от ШИС и направления вращения при коэффициенте заполнения *D = 0,33 (33%)*

Рисунок 25 - Структурная схема блока силовой платы

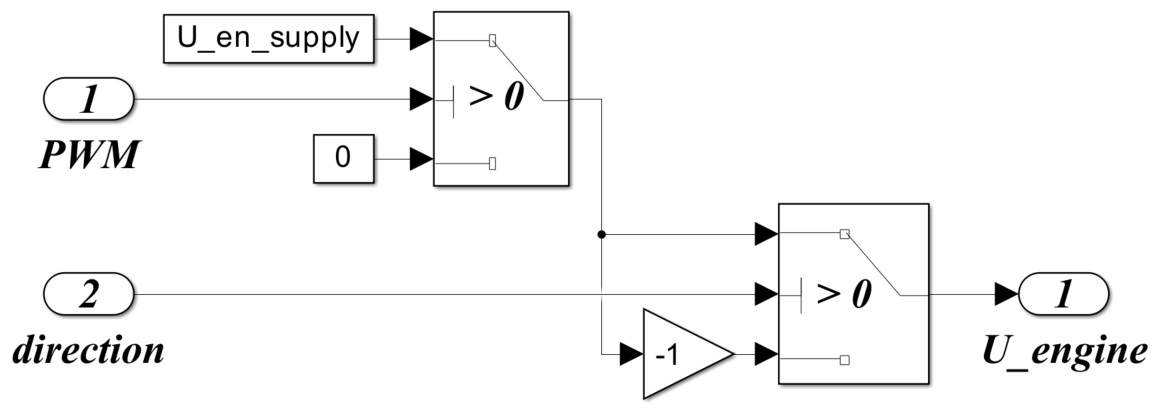
Драйвер описывается уже полученным уравнением (4). По сути он усиливает напряжение до 27 В. В математической модели логика его работы реализована очень упрощённо (рисунок 25).

Помеха потенциометра

На данном блоке долго останавливаться не будем. На рисунке 26 представлена его структурная схема, параметры приведены в скрипте (mat_model.mlx) репозитория проекта на GitHub.

Рисунок 26 - Структурная схема блока помехи

Рисунок 27 - Место получения графиков при моделировании помехи

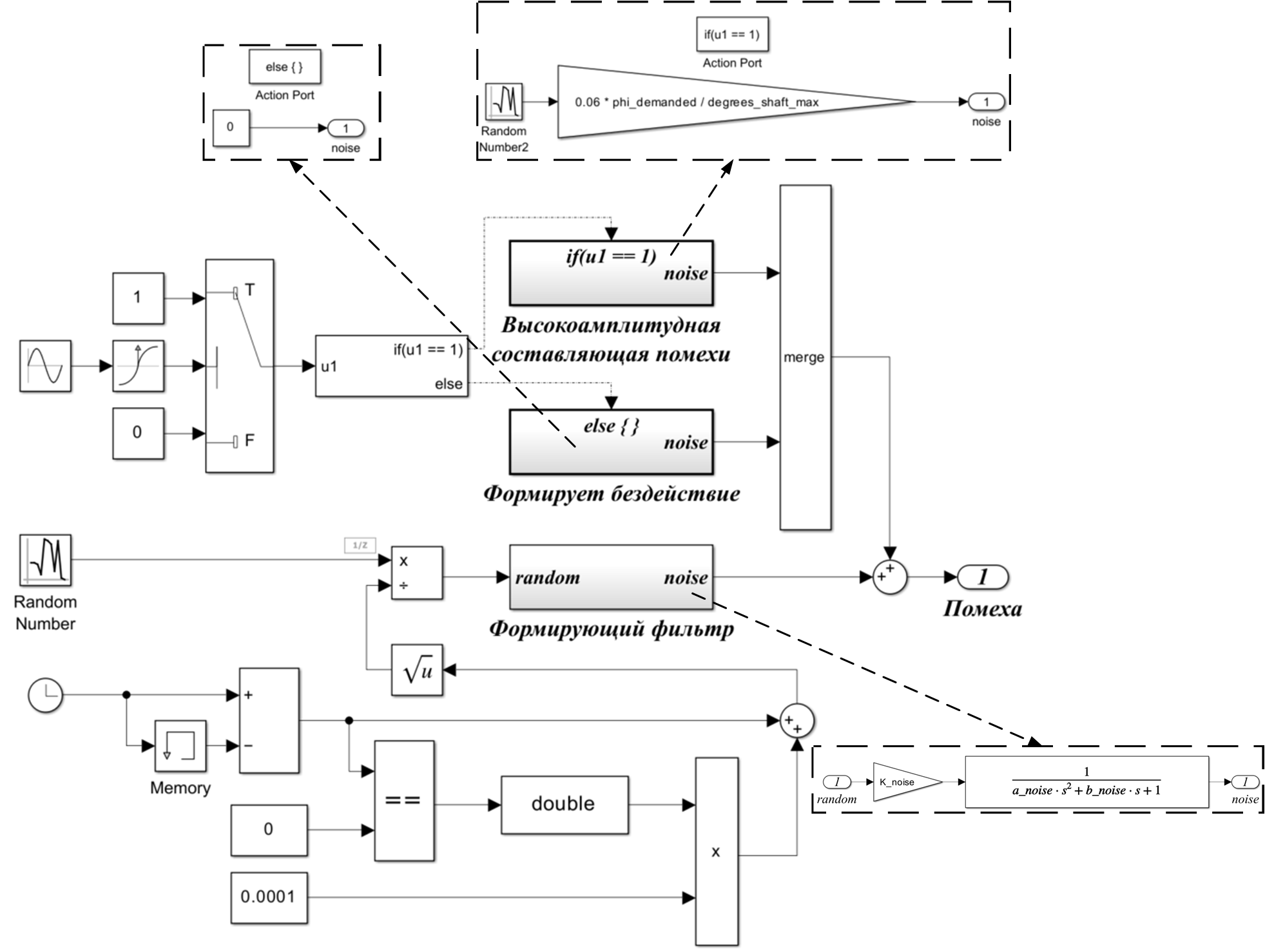
Промоделировав в Simulink при требуемых углах $1^{\circ} \, и \,\, 30^{\circ}$ , были получены результаты (рисунок 28). Помеха – величина постоянная, поэтому кажется, что при 1 градусе она больше, чем при 30, но это не так, ведь для 30 градусов масштаб другой.

Рисунок 28 - Результаты моделирования влияния помехи (чёрный график - сигнал потенциометра, красный график - зашумлённый сигнал)

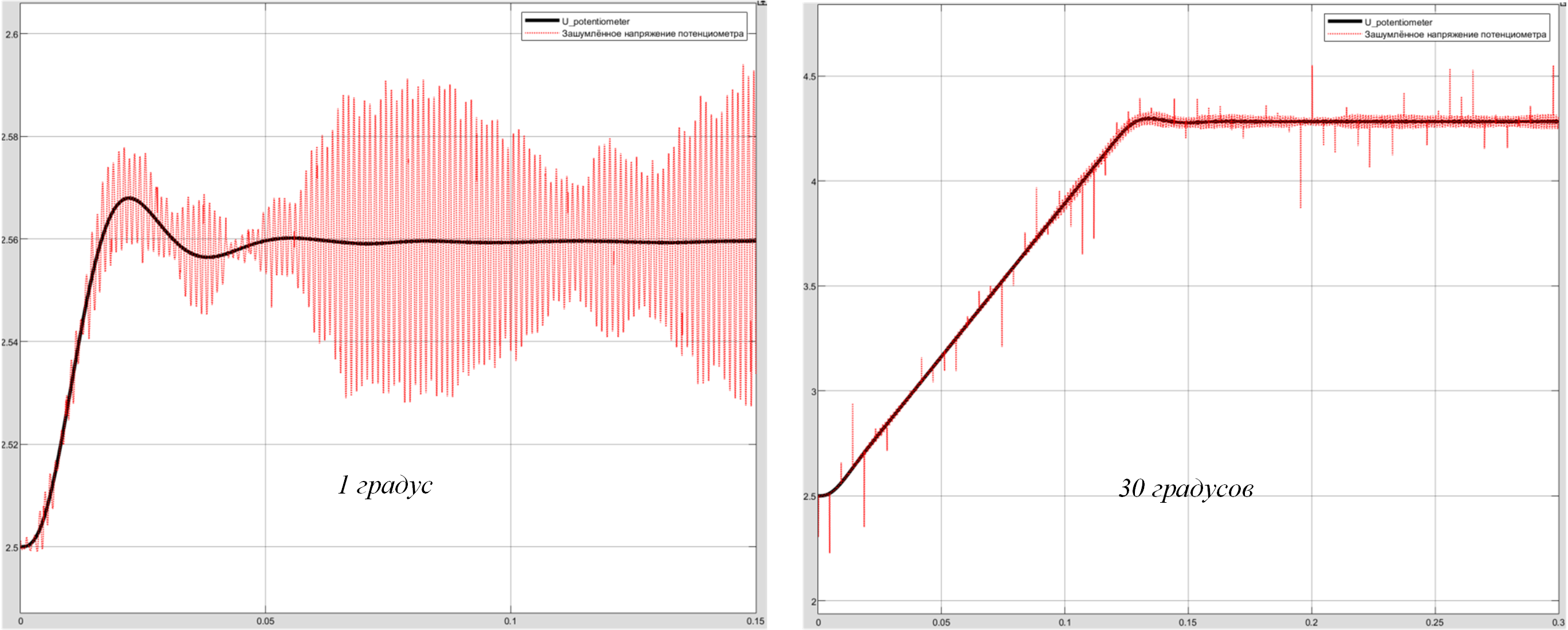
5. Результаты математического моделирования

Система работает по воздействию: какой угол задали, такой и должен быть на выходе. Но так как в системе присутствуют нелинейности (цифровая система, насыщение электродвигателя, помеха и т. д.), выходной угол будет отличаться от требуемого. Для оценки этого отличия и динамических качеств на систему воздействуют тестовыми сигналами определённой формы.

5. 1. Ступенчатое воздействие (переходный процесс)

Промоделируем ступенчатое воздействие для требуемых углов $\varphi_{in} = 1^{\circ} \, и \,\, 30^{\circ}$ .

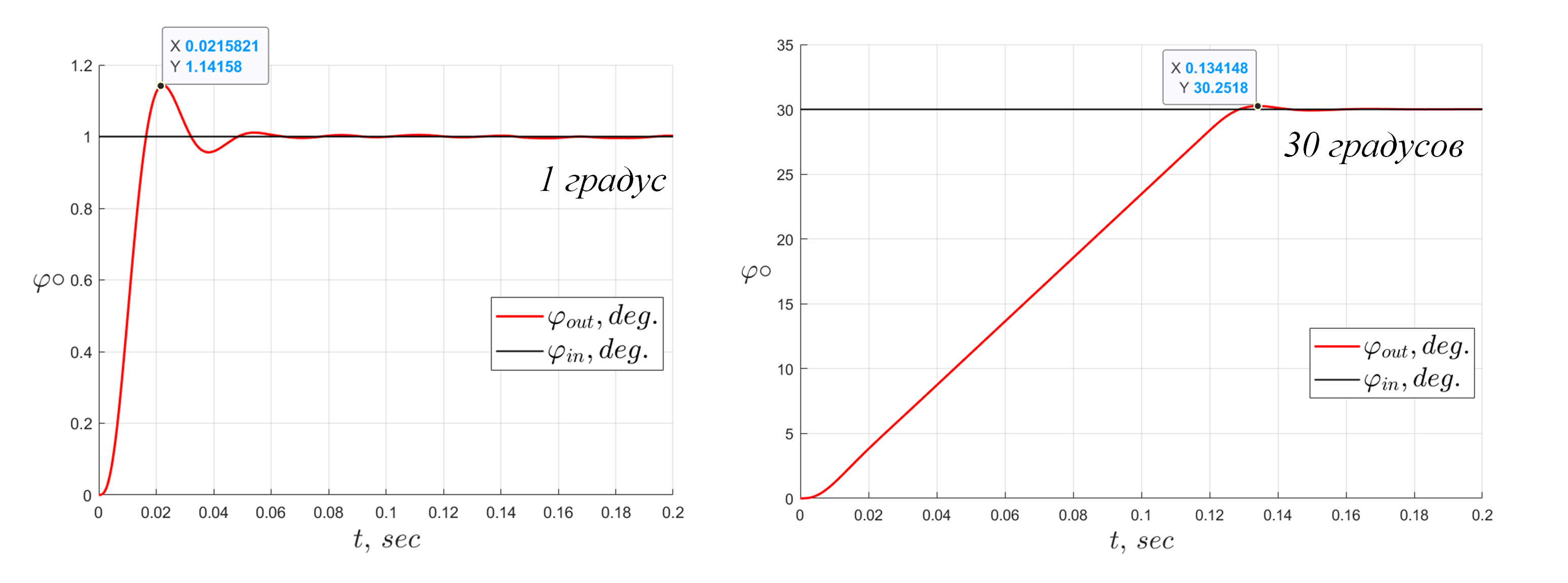
Видно, что система устойчивая. Также из графиков можно сделать вывод о перерегулировании, показателе колебательности и времени переходного процесса. Вычисления приведены для $\varphi_{in} = 1^{\circ}$ ( $\varphi_{in}-$ требуемый угол, $\varphi_{out}-$ текущий угол поворота выходного вала привода). Перерегулирование:

$\sigma = \frac{max(\varphi_{out \,}) - \varphi_{in}}{\varphi_{in}} \cdot 100\% = 14 \%$

Показатель колебательности:

$M = \frac{max(\varphi_{out})}{\varphi_{in}} = 1,14$

где $\varphi_{in} \text{ и } \varphi_{ out} -$ амплитуды требуемого и отработанного углов.

Время переходного процесса при повороте на 30 градусов составляет $t_{пп} = 0,135 \, с$ , что удовлетворяет требованиям.

При движении до 30 градусов видно, что привод вышел на максимальную скорость (наклон прямой = const) - это энергетический предел (насыщение по напряжению двигателя). Если бы напряжение питания двигателя было больше, то привод быстрее бы пришёл в требуемое положение.

Рисунок 30 - Реакция системы при разных коэффициентах усиления

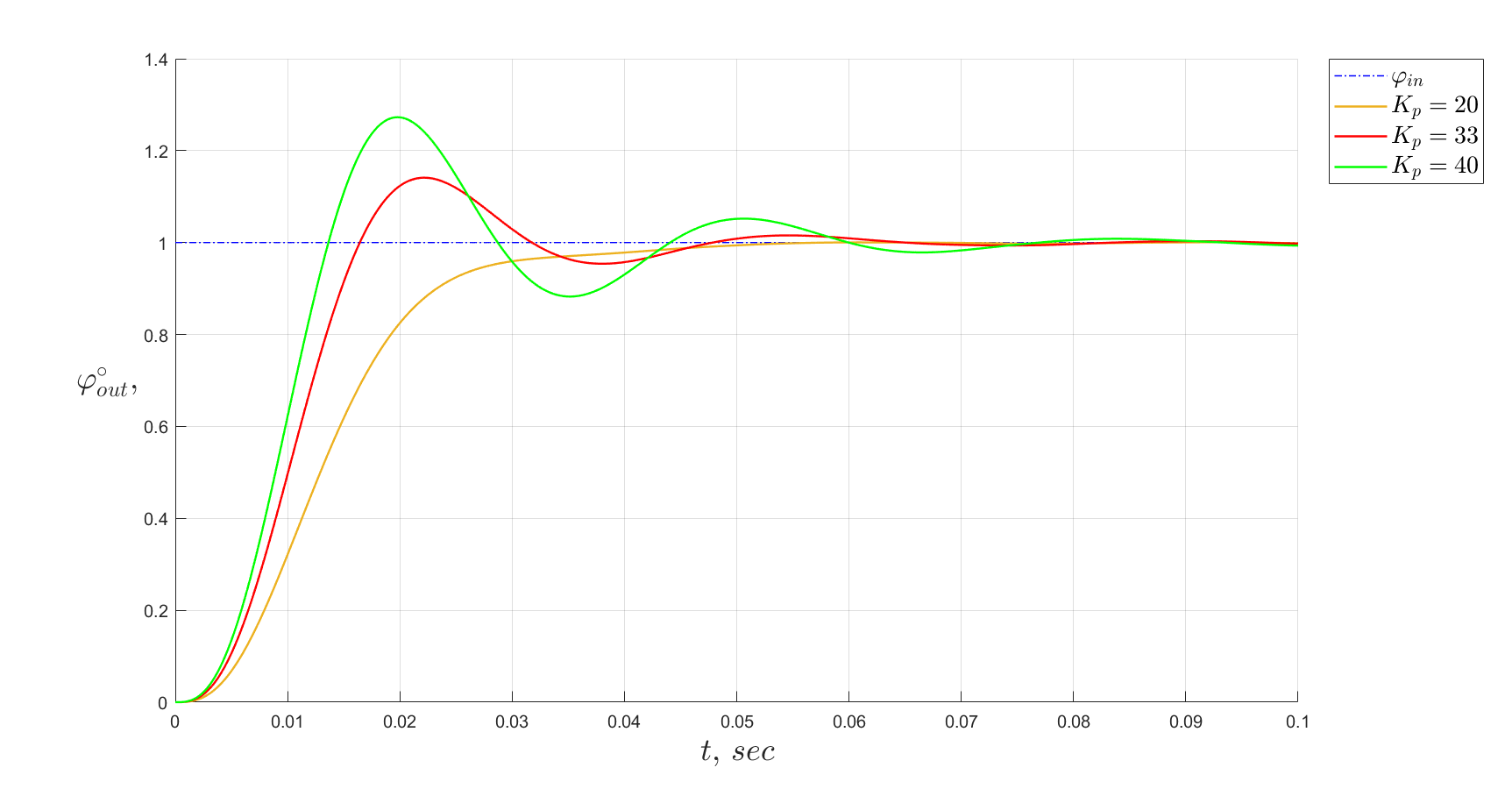
При коэффициенте усиления перерегулирование превышает требуемое значение, при все показатели в норме, однако полоса пропускания меньше, чем 14 Гц. Поэтому был выбран коэффициент усиления .

5. 2. Гармоническое воздействие

При таком типе входного сигнала можно судить о быстродействии системы, иными словами, о её полосе пропускания. Чем больше полоса пропускания, тем привод более динамичный. Входной заданный угол изменяется по гармоническому закону:

$\varphi_{in} = \varphi_{in \, max} \cdot sin((2 \pi f) \cdot t)$

При этом выходной угол до частоты среза $f_{ср}$ будет изменяться тоже по гармоническому закону:

$\varphi_{out} = \varphi_{out \, max}(f, ...) \cdot sin((2 \pi f) \cdot t + \beta)$

Рисунок 31 - Реакция системы на гармоническое воздействие

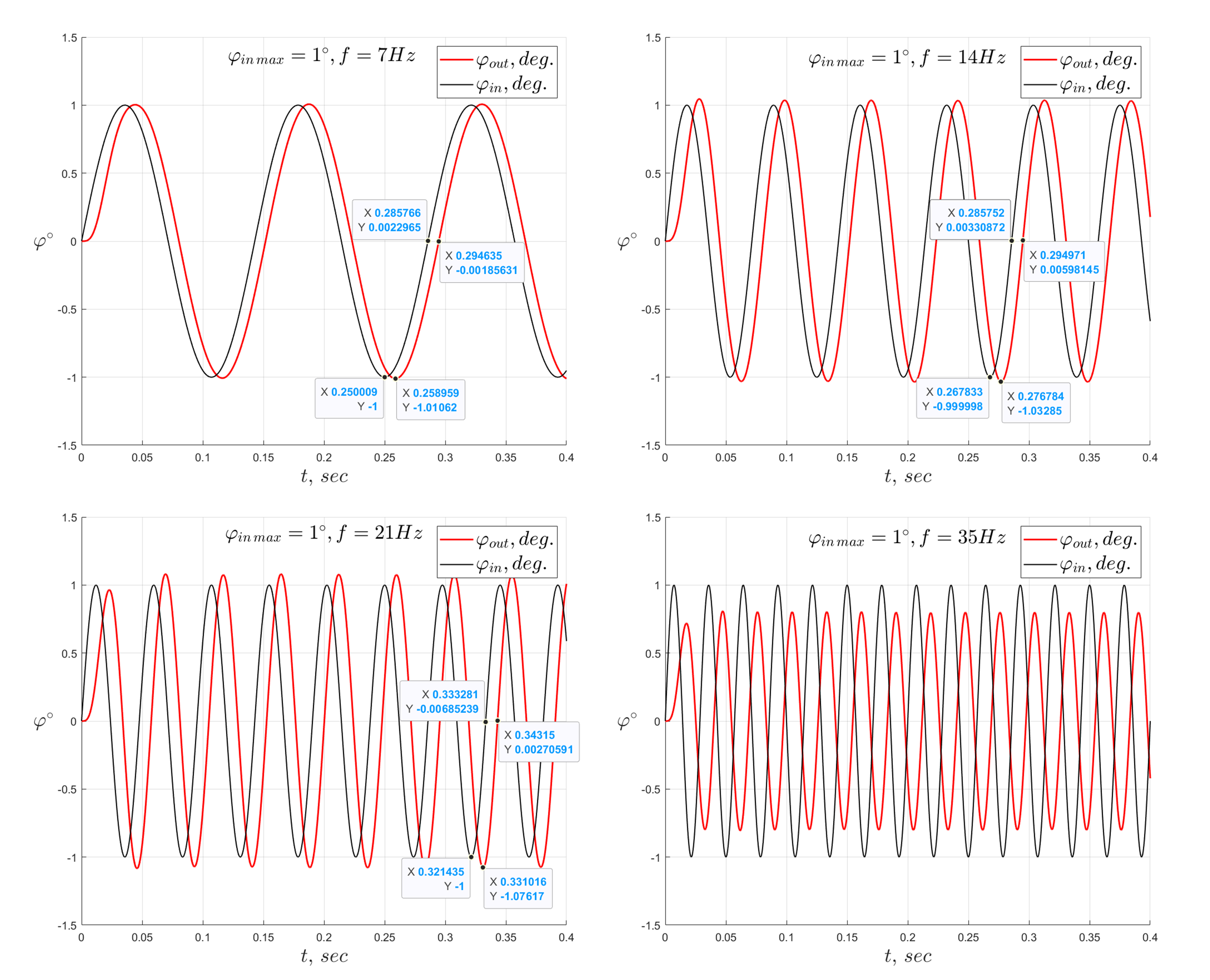
Чем больше частота , тем у привода меньше времени, за которое ему необходимо повернуться на угол $\varphi_{in \, max}$ . И из-за того, что есть энергетическое ограничение, с увеличением частоты входного сигнала привод будет всё хуже его отрабатывать. Из задания необходимо, чтобы при требуемой амплитуде $\varphi_{in \, max} = 1^{\circ}$ частота среза системы была равна $f_{ср}=14 \, Гц$ . Частоту среза, как вариант, можно определять по ЛАФЧХ разомкнутой системы. На графике (рисунок 31) выделены некоторые значения, по которым можно определить проседание мощности выходного сигнала относительно входного и запаздывание по фазе.

5. 3. ЛАФЧХ

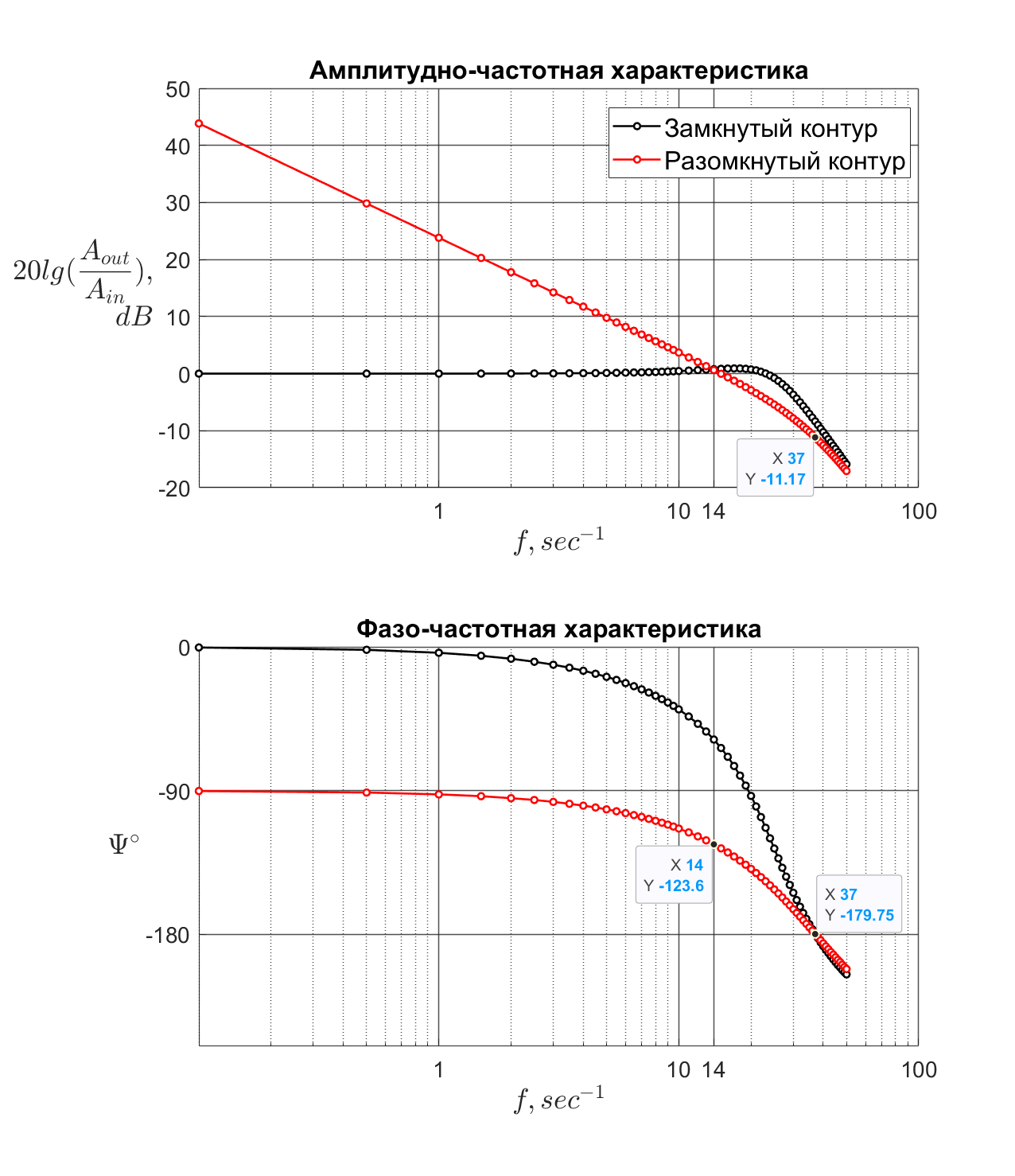
Частота среза (красный график) равна 14 Гц. Это было достигнуто при помощи подстройки коэффициента усиления ПИ-регулятора. Запас по фазе:

$\triangle \Psi = \mid- 180^{\circ} - \Psi_{ср} \mid = \mid -180-(-123,6) \mid = 56,4^{\circ}$

где $\Psi_{ср}-$ фаза на частоте среза. Система устойчива на требуемой частоте среза и имеет запас по фазе $56,4^{\circ} > 50^{\circ}-$ удовлетворяет требованиям.

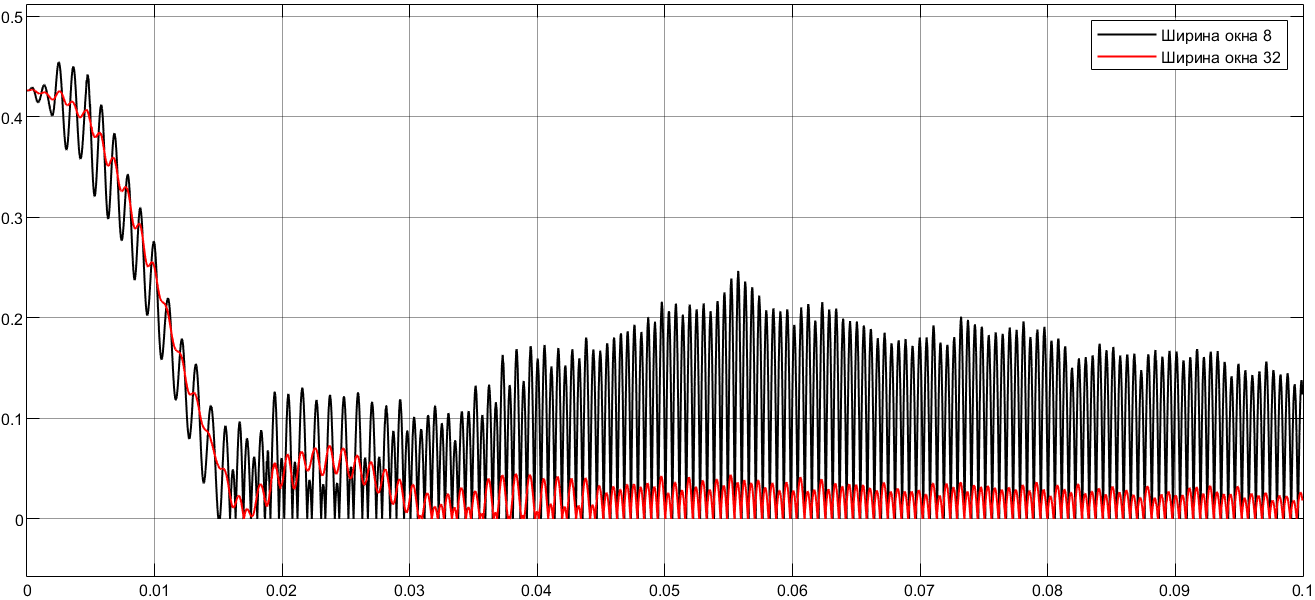
5. 4. Фильтрация

Рисунок 33 - Фильтрация зашумлённого сигнала с потенциометра при ширине окна - 32

Рисунок 34 - Зависимость момента двигателя от ширины окна

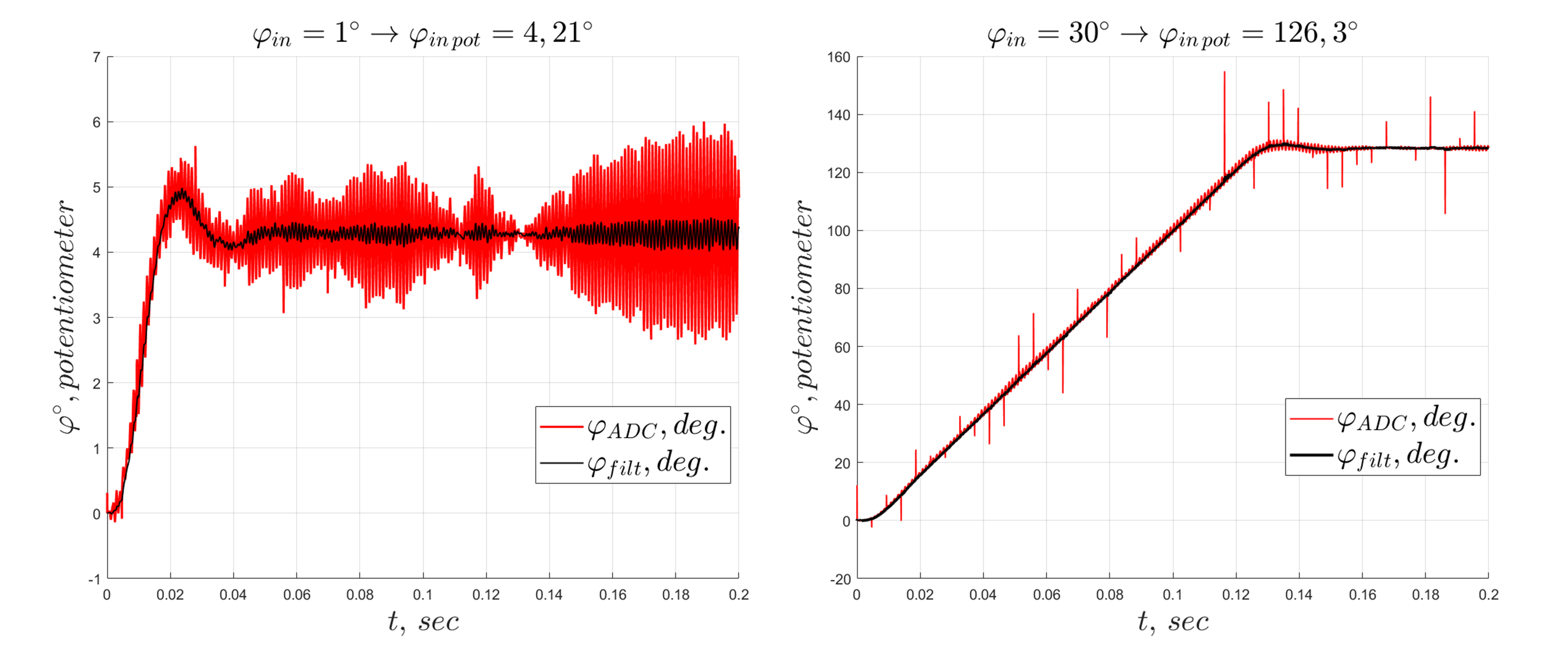
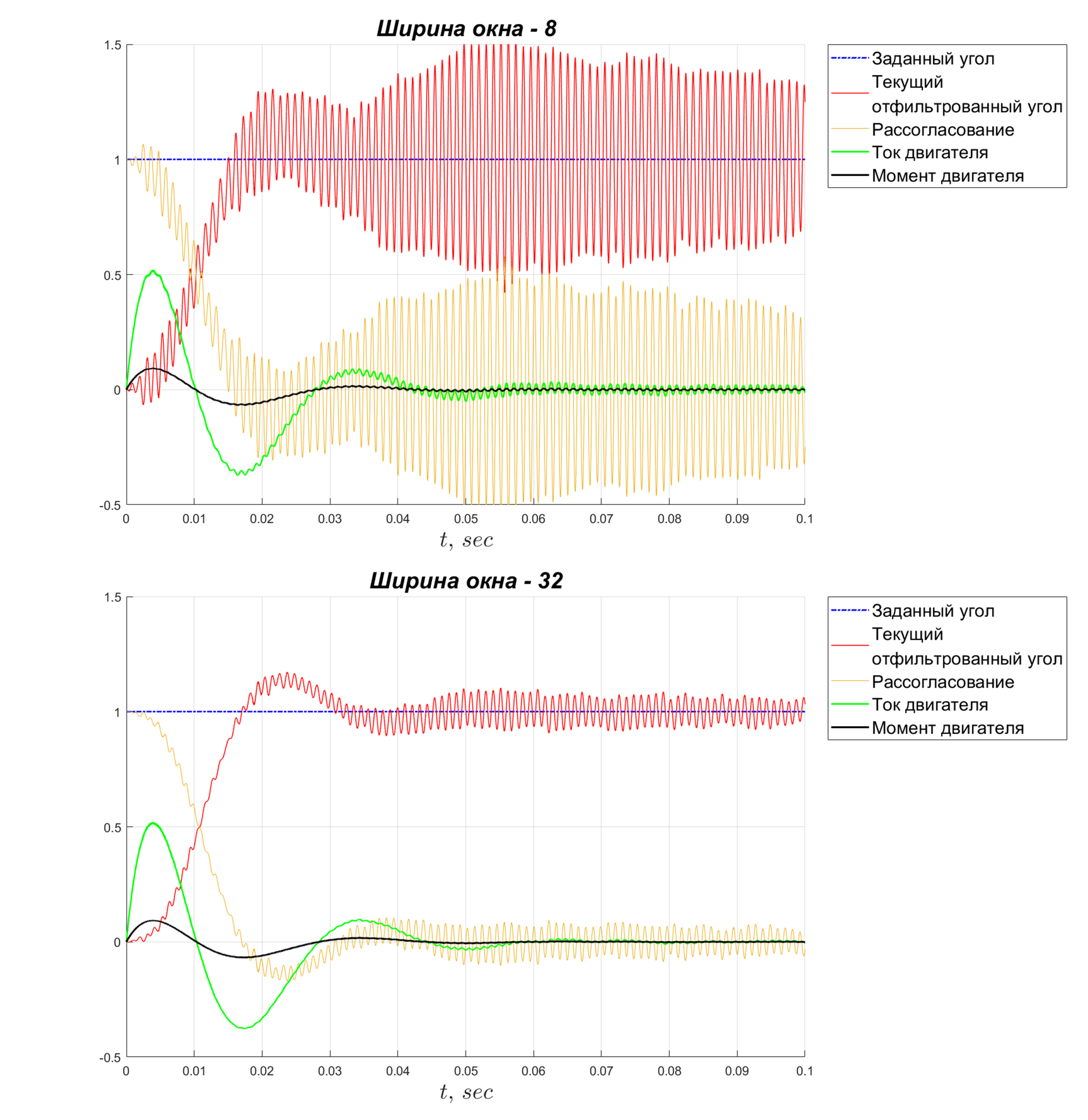
Из-за плохой фильтрации возникают пульсации тока в двигателе и, следовательно, момента. По этой причине выходной вал двигателя будет совершать высокочастотные колебания малой амплитуды – появится звук дребезга в редукторе.

Рисунок 35 - Зависимость коэффициента заполнения ШИС от ширины окна фильтра

6. Выводы

Разработана математическая модель системы автоматического регулирования, управление которой происходит по углу. Были экспериментально и теоретически определены её параметры, а также реализован алгоритм:

цифровой фильтрации;
цифрового ПИ-регулятора;
управления двигателем при помощи ШИМ сигнала.

Проведён поиск параметров, благодаря которым система стала удовлетворять техническому заданию. Также были проанализированы результаты математического моделирования.

В следующей статье будет подробно разобрана реализация данного алгоритма управления на FPGA и приведён сравнительный анализ экспериментальных данных с данными, полученными при моделировании работы приводной системы.

Ссылка на исходники: https://github.com/Dileon44/Actuator-Control-Electronics/tree/main

7. Литература

Комментарии (14)

iqp
01.04.2024 12:30
#26674959
+1
Механическая часть (рисунок 1) состоит из следующих элементов: исполнительного двигателя (ИД), в качестве которого используется коллекторный электродвигатель постоянного тока – ДПР 62-Н4-01

Я не нашел инфу, что к этому двигателю можно применять ШИМ. Вдруг чего-нибудь заклинит, как на тех Боингах.

"Двигатели ДПР-Н5, ДПР-Н9, ДПР-Ф5, ДПР-Ф9 предназначены для работы также при питании от широтноимпульсного модулятора, обеспечивающего среднее значение напряжения на выводных концах двигателя 20 В; частоту следования импульсов не менее 500 Гц и кважность импульсов не менее 0,2; форма импульса - прямоугольная."
1. mphys
  01.04.2024 12:30
  #26676397
  К любым древним двигателям постоянного тока можно применять ШИМ, ничего не заклинит, не беспокойтесь
  1. iqp
    01.04.2024 12:30
    #26682573
    К любым древним двигателям постоянного тока можно применять ШИМ, ничего не заклинит, не беспокойтесь
    
    Пацаны из контрразведки НКВД интересуются - огласите весь список актуальных изделий, в которых под ШИМом стоят моторы, по которым в документации явно нет инфы, что это разрешено. Репрессировать военприемщиков собираются за халатность, а может и не за халатность.

Anatol_1962
01.04.2024 12:30
#26675369
+1
Рис 11 крайне подозрителен. Обычно "мёртвая зона" моторов/клапанов намного шире, и никакой ШИМ этого не исправит. Моделировать мотор "гладким" образом недопустимо для серьёзных инженеров.
1. PoliThor
  01.04.2024 12:30
  #26676461
  Так это же экспериментальная, естественная регулировочная характеристика коллекторного двигателя, полученная без применения всякого ШИМа. Подаёшь напряжение и снимаешь положение -> скорость. Мёртвая зона для такого двигателя, у которого то напряжение питания всего 27 В более чем нормальная.
1. FGV
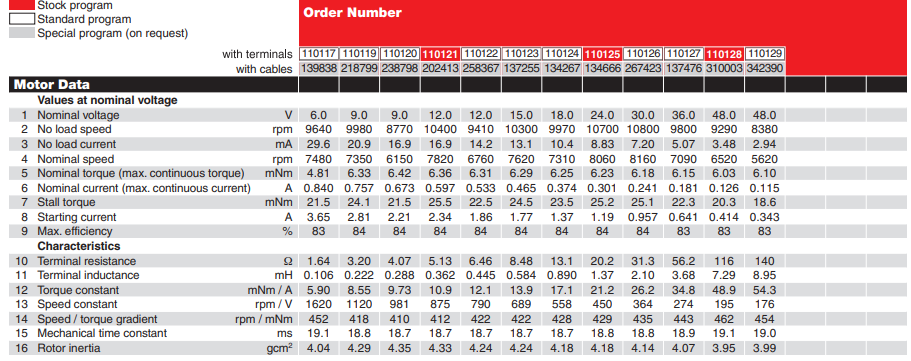
  01.04.2024 12:30
  #26679695
  Ну почему же недопустимо, вот буржуи аж в даташитах на моторы некоторые константы приводят, в том числе и скоростную об/мин. / В (п.13):

Arastas
01.04.2024 12:30
#26675701
+3
Если у вас задачей является смена положения, то подавать 30 градусов ступенькой с выходом на насыщение по питанию, перерегулирование и потенциальное насыщение интегратора - не лучшая идея. Там нужен задатчик траектории.

nv13
01.04.2024 12:30
#26676531
1. Так ли тут нужен fpga? У микроконтроллера уже есть АЦП и линии ввода вывода под ШИМ, watchdog и интерфейсы для подключения к хосту
2. Фильтр с прямоугольным окном можно реализовать как аккумулятор накапливающий N отсчётов, линии задержки на N и вычитателя - каждый входной отсчёт суммируется с аккумулятором, а предNный - вычитается. Большее подавления могут обеспечить каскадные фильтры меньшей длины. Ну и по Найквисту частота дискретизации должна быть не сильно больше удвоенной полосы, зачем Вам всё это на 20 кГц? Данные с датчика можно оцифиовывать с учётом полосы помех, а управление осуществлять в соответствие с эээ.. забыл как это называется.. полосой пропускания без обратной связи?
1. Dileon44 Автор
  01.04.2024 12:30
  #26676693
  Согласен, проще реализовать на МК, однако, как минимум, в авиации в целях резервирования существуют требования на разные элементные базы (то есть, в одной системе есть или МК, и FPGA , или 2 FPGA, или 2 МК: одно управляет, другое следит за правильностью управления), поэтому задачи реализации СУ для привода на FPGA есть. К тому же, этот проектик был больше исследовательским, чем реальным, и ясное дело, что в ракете уж точно целесообразнее использовать МК.
  
  Да, знаю про реализацию с накоплением, но решил сделать так. Про частоту дискретизации: на рисунке представлены экспериментальны данные при периоде одного отсчёта 700 мкс и периоде фильтрации $\rightarrow T_ф = 32 * 700 = 0.22 \, мс$ . Во время отработки при таком периоде привод совершал автоколебания малой амплитуды (красный график), был звук дребезга, явно ведь запаздывание по фазе большое при таком периоде. Поэтому решил уменьшить период.
  
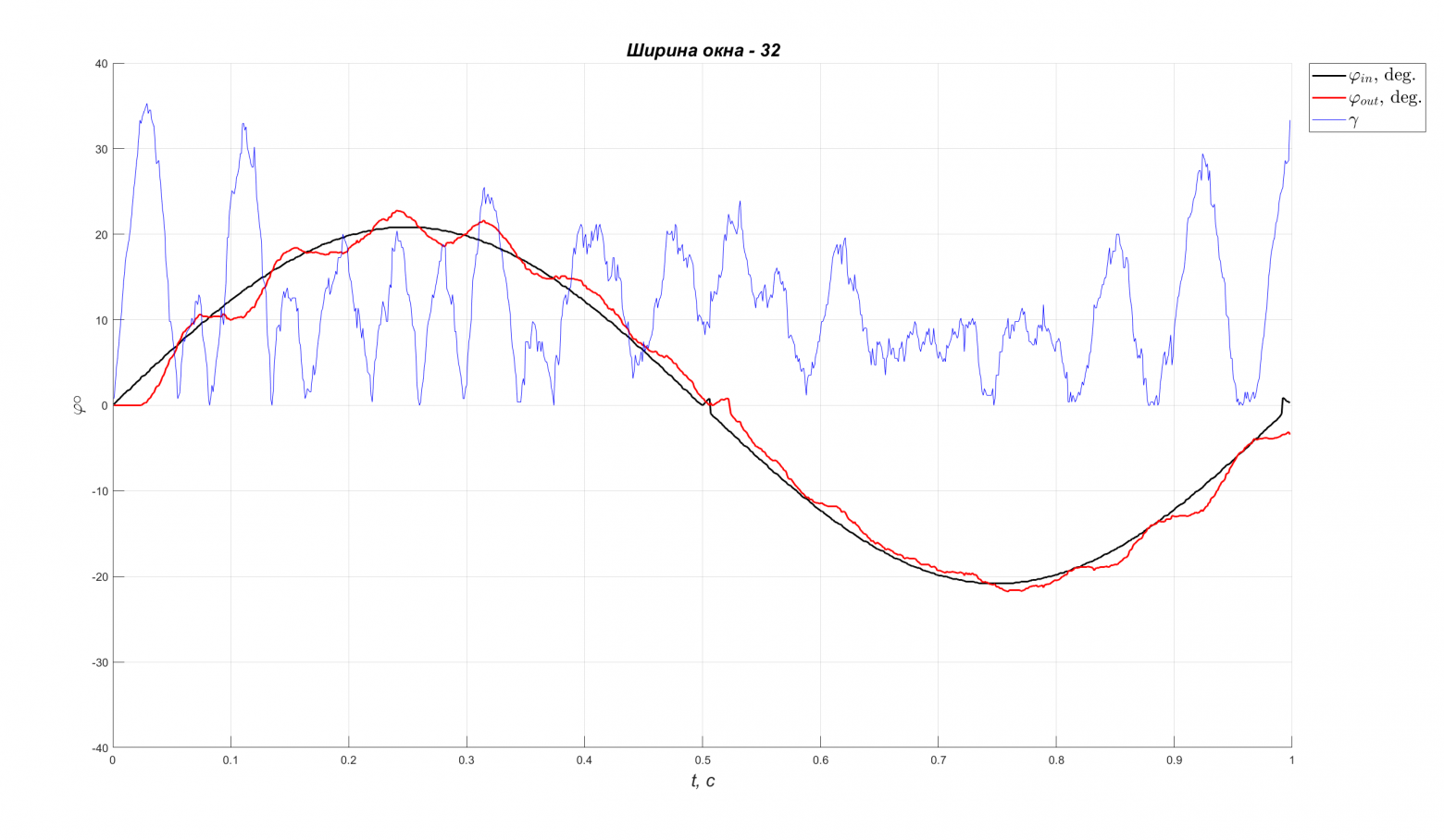
  Реакция на гармоническое воздействие при фильтрации с периодом отсчёта 700 мкс (синий график - коэффициент заполнения ШИМ).
  В ЦОС, к сожалению, не силён, предполагаю, что в моих рассуждениях действительно могут быть ошибки.
  1. nv13
    01.04.2024 12:30
    #26676873
    Попробуйте при частоте 20кГц заменить один фильтр с 32 отсчётами двумя по 16 или тремя по 8, а потом брать только каждую 4-ю выборку и на этой частоте проводить регулирование
    
    К сожалению с радиоавтоматикой, тем более цифровой, я не сталкивался уже очень давно.

BrazilMaterializator
01.04.2024 12:30
#26677309
+1
Почему бы не сделать управление стиральной машиной, а не малогабаритной ракетой? Уже и детские коляски появились на литиевых аккумуляторах, но вы всё на смерть работаете.
1. NutsUnderline
  01.04.2024 12:30
  #26677409
  +1
  А разве автор не детскую (точнее студенческую) игрушку делает?
  1. 200sx_Pilot
    01.04.2024 12:30
    #26679419
    Судя по исполнению редуктора, детей эта "игрушка" не пожалеет.
    
    Интересно, применим ли данный алгоритм для стиральной машинки-автомата. Верхней загрузки.
    
    osmanpasha
    01.04.2024 12:30
    #26679875
    Дак это же управление положением вала с помощью мотора. Скорее как руль в лодке можно применить, чем как мотор в стиральной машине.