CORDIC — это алгоритм для вычисления тригонометрических функций вроде
sin, cos, tan и тому подобных на маломощных устройствах без использования модуля обработки операций с плавающей запятой или затратных таблиц поиска. По факту он сводит эти сложные функции до простых операций сложения и битового сдвига.

Перейду сразу к делу и скажу, почему я так сильно люблю этот алгоритм, а затем займёмся изучением принципов его работы. По сути, фактические операции CORDIC весьма просты — как я уже сказал, это сдвиги и сложение — но выполняет он их путём комбинирования векторной арифметики, тригонометрии, доказательств сходимости и продуманных техник компьютерных наук. Лично я считаю, что именно это имеют ввиду, описывая его природу, как «элегантную».

Начнём с очевидного: если вы работаете на производительном оборудовании, то вам всё это не нужно. Настоящая техника предназначена именно для встраиваемых средств, в особенности малопроизводительных микроконтроллеров и ПЛИС (программируемая логическая интегральная схема). И даже в этом случае есть вероятность, что будут доступны более мощное оборудование или периферийные устройства, способные работать «быстрее», но здесь важно учитывать, что полезность измеряется не только скоростью.

▍ Избегание плавающей запятой

Если тема чисел фиксированной запятой вам уже знакома, можете этот раздел пропустить.

У вас может возникнуть вопрос, каким образом нам удастся избежать плавающей запятой, когда функции вроде sin(x) создают значения в диапазоне от -1,0 до 1,0? Что ж, плавающая запятая — это не единственный способ представления рациональных чисел. В действительности, до популяризации стандарта IEEE 754 всегда использовалась именно фиксированная запятая (можете спросить разработчиков из геймдева, которые создавали игры между 1980-ми и 2000-ми годами).

Лично я сильно погрузился в изучение CORDIC после прослушивания фантастического подкаста Дэна Мангума, посвящённого Microarch Club. В нём Филип Фрейдин обронил острую фразу, мол: «Плавающая запятая — это костыль», а её использование может быть признаком того, что вы не особо понимаете алгоритм, с которым работаете. Естественно, нужно пояснить, что всё это было сказано в контексте обсуждения кастомных ASIC-карт, а не типичных веб-приложений, но сама фраза меня сильно зацепила.

Как же работает фиксированная запятая? Мы берём целочисленный тип вроде int32_t и обозначаем его старшие 16 бит как целую часть, а младшие 16 бит — как дробную. Это число можно поделить и по-другому (например, 10 бит выделить под целую часть, а 22 под дробную), но мы в качестве примера используем соотношение 16/16.



Таким образом мы получаем диапазон примерно от -32768,99997 до 32767,99997. Мы зафиксировали запятую в позиционном представлении числа на 16 битах, хотя, опять же, можно было поставить её в любом месте. Перемещение запятой позволяет нам при необходимости корректировать точность (то есть выделять больше битов для целой части или дробной).

Здесь важно отметить, что число по-прежнему int32_t — и мы, как программисты, внесли сюда дополнительный смысл (хотя это можно сказать почти про любой тип данных в информатике — в итоге мы работаем именно с битами).


Как привести число в этот формат? Что ж, у нас есть 16 бит дробного представления, значит, берём значение, например 42,01, и масштабируем его на (1 << 16). После приведения к типу int32_t это даёт нам 2753167. Если мы захотим вернуться от фиксированной запятой к плавающей, то делаем обратное: 2753167 / (1 << 16) даёт ~42,0099945, что очень близко к 42,01.

#define SCALING_FACTOR (16)

static inline int32_t fixed_from_float(float a) {
  return (int32_t)(a * (float)(1 << SCALING_FACTOR));
}

static inline float fixed_to_float(int32_t a) {
  return (float)a / (float)(1 << SCALING_FACTOR);
}

Также можно полностью отказаться от плавающей запятой и закодировать число, например 1,5, вручную. Его целая часть — это 1, её мы масштабируем на ((1 << 16)), а дробная часть представляет середину между 0x0000 и 0x10000, то есть это будет 0x8000. Таким образом, в десятичном виде мы получим 98303.

Операции вроде сложения и вычитания работают без проблем (в оригинале «Just Work™», — прим. пер.) — при условии использования для всех чисел одного и того же коэффициента масштабирования. Коэффициенты масштабирования можно смешивать и сопоставлять, но это привносит лишнюю сложность.

С умножением процесс будет лишь немного запутанней. Умножение между собой двух чисел с фиксированной запятой, по сути, ведёт к увеличению всего на коэффициент масштабирования. Обратить это действие можно простым сдвигом результата назад.

static inline int32_t fixed_multiply(int32_t a, int32_t b) {
  return ((int64_t)a * (int64_t)b) >> SCALING_FACTOR;
}

Деление, в принципе, работает также, только в обратную сторону. Есть приём, позволяющий повысить точность за счёт предварительного увеличения делимого на коэффициент масштабирования с последующим делением на делитель.

static inline int32_t fixed_divide(int32_t a, int32_t b) {
  return ((int64_t)a << SCALING_FACTOR) / (int64_t)b;
}

Хорошо, с базовыми операциями разобрались. Но что, если мне нужно нечто посложнее, например, тригонометрическая функция? Здесь-то и появляется CORDIC.

▍ Алгоритм CORDIC

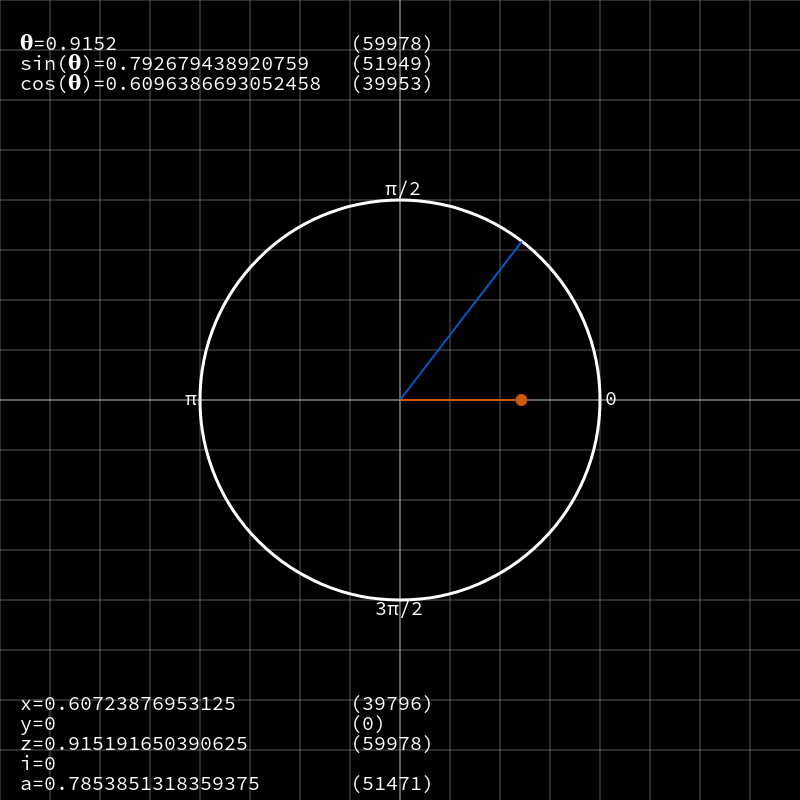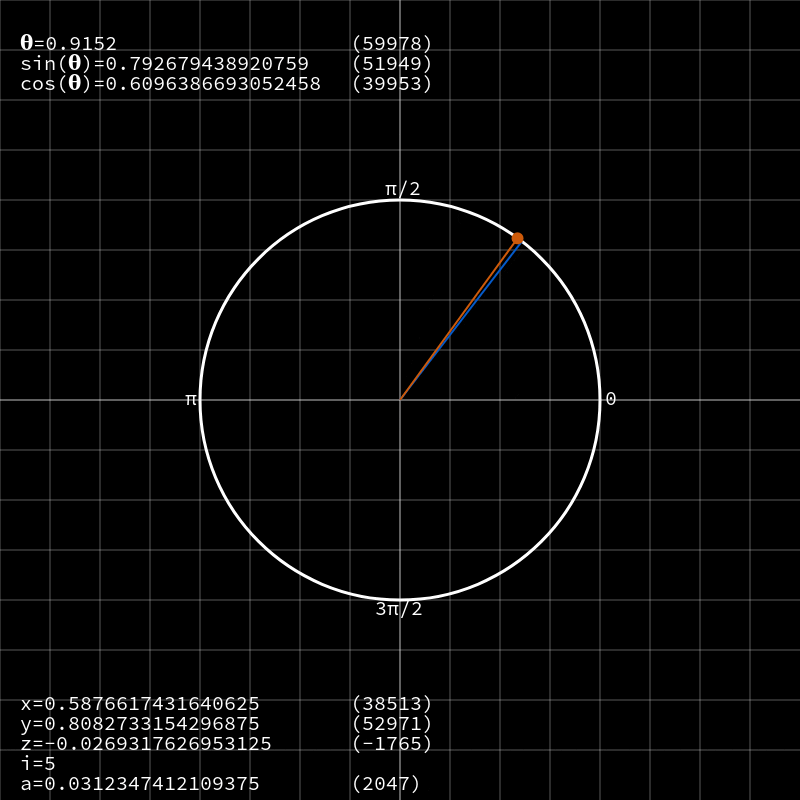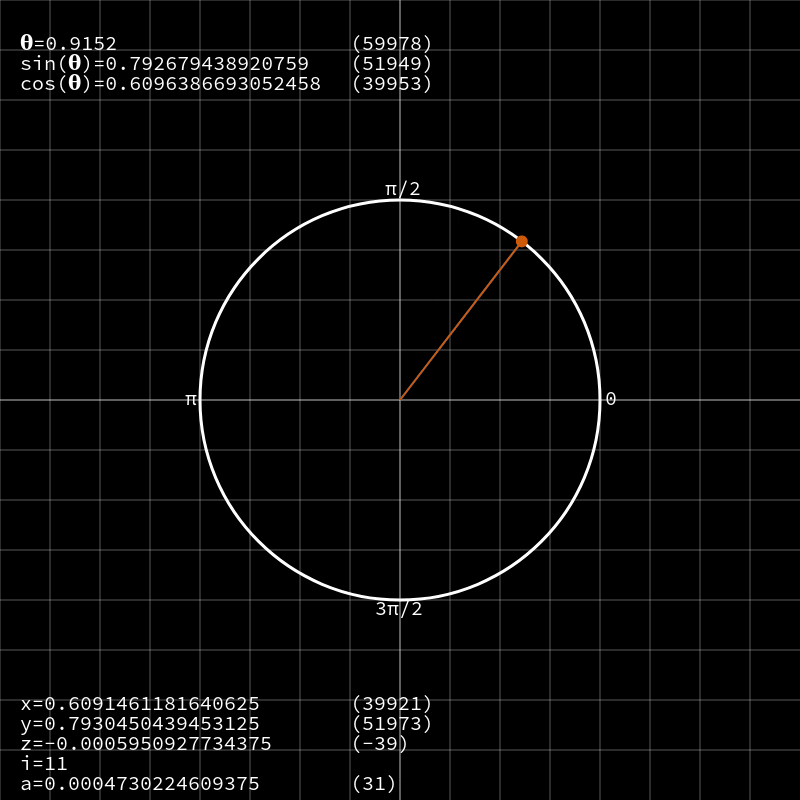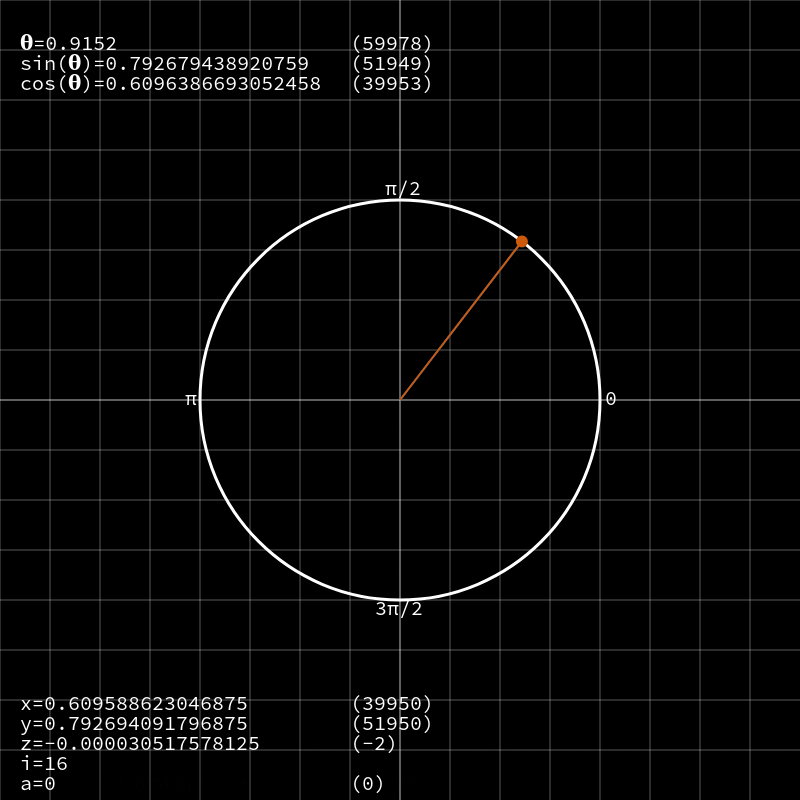
CORDIC означает «co-ordinate rotation digital computer» (цифровой вычислитель поворота в системе координат) и был придуман в середине 50-х (хотя общий его принцип был известен математикам не одну сотню лет). Основная идея в том, что мы можем поворачивать вектор вокруг единичной окружности на всё меньшие углы, и в результате компоненты вектора окажутся синусом и косинусом нужного нам угла.


Это подобно двоичному поиску: вы передвигаетесь к целевому углу на некий большой угол и проверяете, оказались ли дальше или ближе него. Затем, в зависимости от положения, сдвигаете вектор на половину изначального угла по часовой стрелке или против неё. Далее процесс неоднократно повторяется с использованием всё меньших углов, пока вектор не сойдётся с целевым результатом.


Если вы уже имели опыт работы с подобными операциями, то знаете, что вращение вектора подразумевает его умножение на матрицу из синусов и косинусов целевого угла. Такой подход может показаться нелогичным, поскольку ими являются функции, которые мы и пытаемся вычислить.


Но пока забудем об этом и представим более общую картину. Сейчас вполне очевидно, что поворот, скажем, на 22,5˚ — это то же самое, что поворот на 45˚ с последующим поворотом на -22,5˚. То есть мы можем разделить вращение на меньшие части — как положительные, так и отрицательные.

Предположим, что максимальный поворот составляет 90˚ (?/2 радиан), и мы пытаемся узнать sin(0,7) (около 40˚). Начиная с вектора (1, 0) и цели в 0,7 рад, мы делаем поворот на 0,7853 рад (45˚) против часовой стрелки.


Теперь цель представляет 0,7 — 0,7853 = -0,0853. Поскольку значение отрицательное, очередной поворот производим по часовой стрелке на 0,3926 рад (22,5˚). Цель стала -0,0853 + 0,3926 = 0,3073, то есть положительна, значит следующий поворот будет против часовой стрелки на 0,1963 рад (11,25˚).



Если продолжить этот процесс в течение 16 итераций, то вектор практически идеально совпадёт с исходным целевым углом. Значение вектора ~=sin(a), а x ~= cos(a)! Именно так работает CORDIC; мы вращаем вектор в разных направлениях, и в качестве состояния сохраняется аппроксимация различных тригонометрических функций.


Имея некоторое понимание, теперь можно вернуться к той самой проблеме, что для поворота вектора необходимы функции, которые мы пытаемся вычислить. Матрицу можно упростить с помощью тригонометрии.


Теперь у нас есть несколько констант, но также по-прежнему есть tan(a) и cos(a). Давайте проигнорируем cos(a) и постараемся избавиться от tan(a). Как вы видели при разборе алгоритма, мы всегда выполняем поворот в общем на ~90˚: сначала на 45˚, затем на 22,5˚, потом на 11,25˚ и так далее. Поскольку мы проделываем это фиксированное число раз, то можно просто заранее вычислить эти значения и внести их в таблицу. Вы можете подумать: «Ты сказал, что не будет никаких таблиц!» Не совсем. Я сказал, что не будет затратных таблиц. Эта же таблица в нашем случае будет содержать лишь 16 чисел uint32_t, занимающих аж целых 64 байта. Даже самые ограниченные встраиваемые решения обычно могут себе такое позволить. (К сравнению, неоптимизированная таблица для sin(x), содержащая 4096 записей значений от -1 до 1, потребует 16 КиБ — и это при довольно низкой точности).


Это означает, что наша матрица вращений содержит только константы. Тем не менее у нас всё равно остаётся член cos(a). В действительности, каждая итерация привносит новый член cos(a). Но, благодаря алгебре, можно просто умножить эти члены друг на друга и применить их в конце.


Хотя и это не очень хорошо. Но! Независимо ни от того, делаем мы положительные или же отрицательные шаги, ни от количества итераций, эта перемноженная серия косинусов по факту сойдётся к константе: ~0,6366. Нам лишь нужно после всех итераций умножить результат на это значение.


Итак, в течение всей серии итераций мы задействуем лишь умножение на константы. Неплохо. Но разве я не говорил, что CORDIC использует только битовый сдвиг и сложение? Для этого нам потребуется чуть глубже заглянуть в его кроличью нору.

▍ Сдвиги и сложение

Можно ли углы, которые мы подставили в tan(a), вместо этого стратегически выбрать так, чтобы результат всегда был равен обратной степени 2? Было бы здорово, поскольку умножение или деление на степень 2 для целых чисел представляет просто сдвиг влево или вправо.

Что ж, это как раз поможет проделать функция atan(x) (арктангенс или обратный тангенс). Можно построить новую таблицу из 16 записей, в которой каждое значение будет равно atan(2**-i) при i в диапазоне от 0 до 15. Теперь фактические значения вращения для каждой итерации будут следующими: 45˚, 26,565˚, 14,036˚, 7,125˚ и так далее.

Здесь каждый раз угол в реальности делится не точно пополам. Но, как оказывается, при использовании этих углов процесс всё равно будет сходиться к одному корректному результату. Теперь все эти умножения на tan(a) стали битовыми сдвигами, соответствующими числу итераций.

Нам по-прежнему нужно повторно вычислить нашу константу для членов cos(a). Сейчас она получится равной примерно 0,60725, и это значение можно преобразовать в число с фиксированной запятой 39796. Кроме того, есть один приём, который избавляет нас от необходимости умножения на это значение в конце. При инициализации вектора нужно установить x не на 1, а на эту константу.


Теперь алгоритм CORDIC выглядит так:

• Предварительно вычисляет таблицу для tan(a), в которой каждая запись представляет atan(2**-i). Эти значения, естественно, преобразуются в числа с фиксированной запятой, значит atan(2**-i) * (1 << 16)
• Затем, когда нам нужно вычислить синус или косинус, мы берём угол (например, 0,9152) и преобразуем его в значение с фиксированной запятой: 0,9152 * (1 << 16) = 59978.

Далее прописываем начальные параметры:

x = 39796
y = 0
z = 59978

Параметр z здесь не является частью вектора. С помощью него происходит отслеживание нашего целевого угла. Знак этого параметра определяет, в каком направлении нужно делать поворот: по часовой или против часовой стрелки.

После настройки параметров каждая итерация в псевдокоде будет выглядеть так:

if z >= 0:
    x_next = x - (y >> i)
    y_next = y + (x >> i)
    z -= table[i]
else:
    x_next = x + (y >> i)
    y_next = y - (x >> i)
    z += table[i]
x = x_next
y = y_next

Теперь можно проделать несколько итераций и посмотреть, как алгоритм сходится к верным значениям синуса и косинуса. Значения в скобках — это значения с фиксированной запятой.


Во время первой итерации z был положительным, поэтому вектор повернулся на ~0,785 рад против часовой стрелки. Заметьте, что при этом он увеличился.


При второй итерации z также оказался положительным, поэтому вектор снова был повёрнут против часовой стрелки, но уже на ~0,436 рад, и на этот раз проскочил целевую отметку. Теперь величина вектора равна почти единице — это произведение cos(a) начинает сходиться после установки изначального значения x.


В третьей итерации z был отрицательным, поэтому вектор повернулся по часовой стрелке на ~0,244 рад. Он явно начинает подбираться к целевой отметке, и вы видите, что до получения очень близкой аппроксимации осталось буквально несколько итераций.


На четвёртой итерации z снова был отрицательным, что привело к повороту по часовой стрелке на ~0,124 рад. Теперь, когда изменение угла становится очень небольшим, и вектор очень близок к нужному результату, операции вращения продолжают гонять его туда-сюда, всё ближе подводя к целевому значению.


Перейдём к последней итерации. Теперь y содержит очень точную аппроксимацию для sin(0.9152) — с абсолютным отклонением всего в 0,00000956. Отклонение значения косинуса (в x) чуть выше и составляет 0,0000434, но всё равно весьма неплохо!

▍ Подытожим

Об алгоритме CORDIC можно сказать намного больше. Возможно, я затрону эту тему в будущей статье. Например, я не упомянул особые нюансы, которые необходимо учитывать, если нужный угол находится вне первого или четвёртого квадранта единичной окружности. Я также не говорил о том, как с помощью нескольких изменений можно настроить CORDIC для вычисления многих других функций, включая tan, atan, asin, acos, sinh, cosh, tanh, sqrt, ln, e^x. Существуют и другие похожие алгоритмы, такие как BKM, созданный специально для вычисления логарифмов и степеней.

Я планирую достаточно детально раскрыть эту тему на своём YouTube-канале Low Byte Productions, так что приглашаю на него всех интересующихся.

Telegram-канал со скидками, розыгрышами призов и новостями IT ?