Всем привет! Меня зовут Максим. Я NLP‑инженер в red_mad_robot и автор Telegram‑канала Максим Максимов // IT, AI. В этой серии статей я расскажу о метриках популярных задач Natural Language Processing (NLP). Первая часть будет посвящена подходам для оценки моделей в решении задач классификации, NER и кластеризации. Рассказ будет сопровождаться визуализацией, примерами и кодом на Python.

Содержание

• Введение

• Классификация

• NER

• Кластеризация

Введение

Важно уметь правильно оценивать свое решение, а также сравнивать его с другими. Бывает соблазн, просто взглянув на работу приложения или модели, сказать: «В целом работает хорошо, другой инструмент мне прошлый раз отвечал хуже». Но эта оценка может быть субъективна. Правильно отвечать на вопросы: «Что значит хорошо?», «Что значит отвечал хуже чем другой инструмент?», «На сколько хуже?».

Для объективной оценки в NLP используются специальные метрики. Они различаются в зависимости от задачи и позволяют количественно оценить качество работы модели.

В этой статье я не буду подробно останавливаться на анализе данных (о котором я рассказывал в своей прошлой статье), подготовке и обучении моделей, а сосредоточусь на метриках и их расчёте с помощью Python.

Классификация

Начнем с одной из популярных задач — классификации. Разберемся с основными метриками классификации.

Возьмем в качестве примера датасет с Kaggle, который представляет собой набор описаний товаров, каждый из которых отнесен к одному из классов: 

• электроника;

• товары для дома;

• книги;

• одежда и аксессуары.

По этому датасету можно сказать, что мы будем решать задачу многоклассовой классификации. То есть, нужно отнести объект (описание товара), к одному из нескольких классов (электроника, товары для дома, книги, одежда и аксессуары).

Загрузим данные и разделим их на обучающую и тестовую выборку. В качестве инструмента будем использовать библиотеку pandas.

import pandas as pd

df = pd.read_csv("./ecommerceDataset.csv", 
                 names=["category", "description"],
                 header=None)
# для упрощения и скорости работы возьмем только 10.000 примеров
df = df.sample(10000)
df.head()

Проведем небольшую чистку данных: удалим дубликаты, пропуски, а также короткие описания (менее 10 символов).

df = df.drop_duplicates()
df = df.dropna()
df = df[df['description'].map(lambda x: len(x)) > 10]

После очистки из 10.000 строк данных у нас стало 8578.

print(df.shape)
#(8618, 2)

Проведем небольшой анализ и взглянем на распределение классов в датасете

df['category'].value_counts().plot(kind='bar')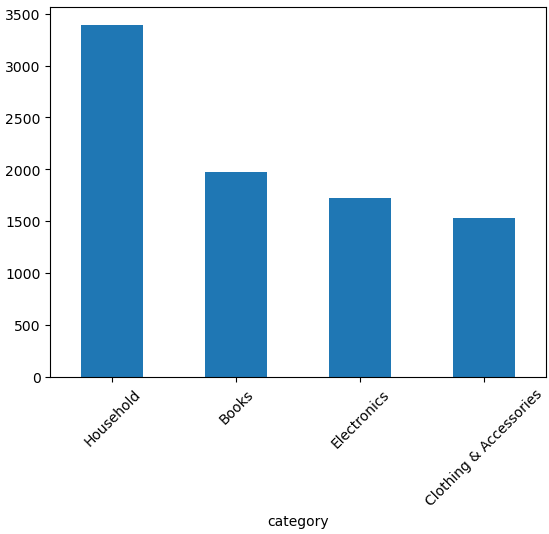

Видим, что имеется дисбаланс классов. А именно: в данных преобладает класс Household над остальными. Это стоит учитывать при подсчете метрик (рассмотрим далее).

Разделим данные на тестовую и обучающую выборки. Во время деления будем использовать "стратификацию" (то есть, чтобы баланс классов в обучающей и тестовой выборке был приблизительно одинаков). Для этого используем функцию train_test_split из sklearn с параметром stratify.

from sklearn.model_selection import train_test_split

train_data, test_data = train_test_split(df, test_size=0.2, stratify=df['category'])
print(f"{len(train_data)=}\n{len(test_data)=}")

# len(train_data)=6894
# len(test_data)=1724

Также переведем классы в числовое представления, для удобства работы. 

d_target = {label:i for i, label in enumerate(list(y_train.unique()))}
y_train_label = y_train.map(lambda x: d_target[x])
y_test_label = y_test.map(lambda x: d_target[x])

Подготовим данные и обучим модель. 

Сделаю небольшую предобработку текста (с помощью spacy): выкину стоп слова, числа и сделаю лемматизацию. После этого векторизую текст, используя sentence_transformer и базовую модель all‑MiniLM‑L6-v2.

import spacy
import sentence_transformers

model = sentence_transformers.SentenceTransformer("all-MiniLM-L6-v2")
nlp = spacy.load("en_core_web_sm")

def prepare_data(text_list):
   # чистка и лемматизация текста
    def _lemmatization_rm_stop_words(text_list):
        result_texts = []
        for text in tqdm(text_list):
            text = text.lower()
            doc = nlp(text, disable=["tok2vec", "tagger", "parser", "attribute_ruler"])
            filtered_tokens = [token.lemma_ for token in doc if not (token.is_stop or token.is_punct or not token.is_alpha)]
            filtered_text = " ".join(filtered_tokens)
            result_texts.append(filtered_text)
        return result_texts	
    
    # векторизация текста
    def _vectorize_texts(text_list):
        embeddings = model.encode(text_list, normalize_embeddings=True, show_progress_bar=True)
        return embeddings

    print("Clearing texts...")
    clear_text = _lemmatization_rm_stop_words(text_list)

    print("Vectorize texts...")
    embeddings = _vectorize_texts(clear_text)

    return embeddings

# Сохранение эмбеддингов
embeddings_train = prepare_data(X_train.to_list())
embeddings_test = prepare_data(X_test.to_list())
np.save("train_embed.npy", embeddings_train)
np.save("test_embed.npy", embeddings_test)

Получаем эмбеддинги текста размерностью 384, которые будем использовать для обучения классификатора. Кстати, если вы не знакомы с понятием «эмбеддинг», я подробно рассказывал об этом в своей прошлой статье.

В качестве классификатора, для простоты, возьмем CatBoost.

from catboost import CatBoostClassifier
model = CatBoostClassifier()

Обучим модель на данных

model.fit(X=embeddings_train, y=y_train_label)

Далее нам необходимо оценить обученную модель на тестовых данных.

Матрица ошибок

Перед тем как посчитать метрики, давайте вспомним, что такое conflusion matrix (или матрица ошибок). Рассмотрим ее на примере предсказаний класса «книги», из наших данных.

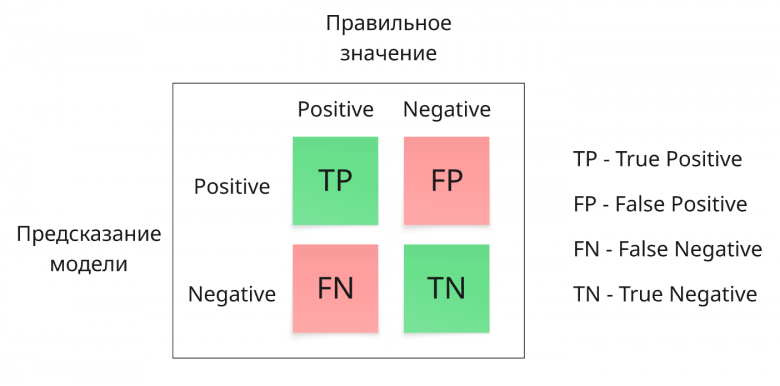
Представим, что мы обучили модель классифицировать данные на 2 класса: 1 — пример из класса «Books», 0 — пример не из класса «Books». 

Далее, делаем предсказания на данных, для которых у нас имеются правильные метки класса. 

В данном случае, можно составить conflusion matrix, в которой:

• True Positive (TP) — Модель предсказала «Books», и товар действительно был из категории Книг.

• False Positive (FP) — Модель предсказала «Books», но на самом деле товар был из другой категории (например, Электроники).

• True Negative (TN) — Модель предсказала «Не Books», и товар не был книгой (относился к одной из трёх других категорий).

• False Negative (FN) — Модель предсказала «Не Books», но на самом деле товар был из категории Книг.

Также на основе conflusion matrix выделяют понятия «ошибка 1 рода» и «ошибка 2 рода». Аналогично:

• Ошибка 1 рода (FP) — Модель предсказывает наличие класса, которого на самом деле нет.

• Ошибка 2 рода (FN) — Модель не обнаружила класс, который на самом деле был.

Давайте составим эту матрицу на основе обученной модели и тестовых данных. 

Получим предсказания модели 

pred = model.predict(embeddings_test)

Далее, мы посчитаем матрицу ошибок для предсказаний класса «Books». Для этого создадим список, в котором «1» обозначим класс «Books», а «0» все остальные. Так будет сделано для предсказаний и реальный тестовых данных. 

new_labels_pred = [1 if label == "Books" else 0 for label in pred.reshape(-1) ]
new_labels_target = [1 if label == "Books" else 0 for label in y_test.to_list()]

Посчитаем матрицу ошибок, используя функцию из sklearn

from sklearn.metrics import confusion_matrix

TN, FP, FN, TP = confusion_matrix(new_labels_target, new_labels_pred).ravel().tolist()
print(f"{TN=}\n{FP=}\n{FN=}\n{TP=}")
# TN=1307
# FP=23
# FN=22
# TP=372

На основе матрицы ошибок, можно получить полезную информацию о работе классификатора. Видим, что модель достаточно хорошо классифицирует класс «Books» от других классов, но все же допускает ошибки 1 и 2 рода. Эти выводы могут быть достаточно абстрактны, поэтому обычно считают конкретные метрики, которые используют для достижения конкретной цели. 

Ниже будут посчитаны основные метрики для задачи классификации описания товаров на 2 класса: «Books» и не-«Books». После я покажу, как происходит расчет тех же метрик для задач многоклассовой классификации (как с той, что мы взяли в начале этой главы). 

Accuracy

Доля правильных ответов среди всех ответов. Она считается по следующей формуле:

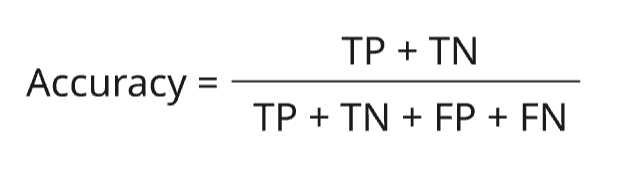
Это одна из самых простых метрик классификации, которая говорит о том, на сколько хорошо модель находит нужные нам классы (в данном случае «Books») из всех ее предсказаний. Она может принимать значения в диапазоне от 0 до 1, где 0 означает, что модель ошибается во всех случаях, а 1 - модель предсказывает все верно.

Посчитаем Accuracy для нашего классификатора

accuracy = (TP + TN) / (TP + FP + FN + TN)
print(f"{accuracy=}")
# accuracy=0.9738979118329466

Для простоты также можно использовать встроенную в sklearn функцию:

from sklearn.metrics import accuracy_score
accuracy_sklearn = accuracy_score(new_labels_target, new_labels_pred)
print(f"{accuracy_sklearn=}")
# accuracy_sklearn=0.9738979118329466

Получаем почти 98% точности. На этом этапе можно было остановиться и сказать, что мы решили задачу на отлично, но есть нюанс. 

Метрика accuracy показывает то, насколько модель правильно классифицировала ВСЕ объекты в выборке. То есть, и класс «Books» и не-«Books». 

В данном случае объектов класса «Books» (TP + FN) в выборке 394, а объектов не-«Books» (TN + FP) - 1330. То есть в выборке присутствует явный дисбаланс классов.

Теперь вместо нашего классификатора возьмем модель, которая всегда предсказывает класс не‑«Books», и посчитаем accuracy у такой модели

model_no_books = lambda x: 0
pred_nb = [model_no_books(el) for el in embeddings_test]

# берем функцию из sklearn
accuracy_nb = accuracy_score(new_labels_target, pred_nb)
print(f"{accuracy_nb=}")
# accuracy_nb=0.771461716937355

Получаем целых 77%! То есть, максимально «глупая» модель получает такое accuracy на наших данных, и все потому, что наши данные не сбалансированы. Если бы для нас было критически важно находить объекты класса "Books", такая высокая accuracy создала бы иллюзию отличной работы модели, хотя на самом деле она не нашла бы ни одного такого объекта.

Делаем вывод: использование accuracy на несбалансированных данных может вводить в заблуждение, создавая иллюзию отличной работы модели, в то время как на самом деле она может плохо справляться с важным, но редким классом. Эту метрику можно использовать, когда требуется интуитивно понятная оценка качества модели, на первых итерациях работы, и когда вы точно понимаете что представляют собой ваши данные.

Precision, Recall и F1

Взглянем еще на одну хорошую визуализацию, которая поможет более интуитивно понять элементы матрицы ошибок, и подсчет метрик на основе них.

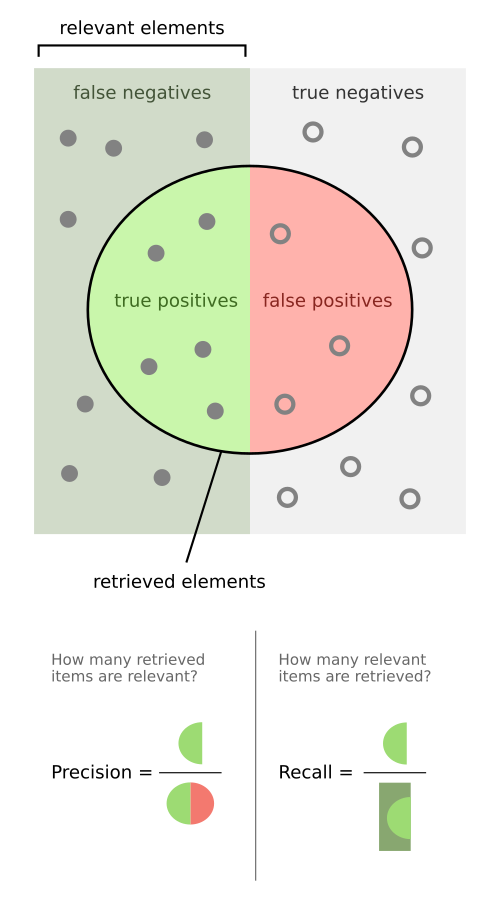
Наглядно видно, что представляет собой Precision и Recall. Давай подробнее взглянем на эти метрики.

Precision

Начнем с Precision. Это метрика, которая показывает долю объектов, верно классифицированных моделью как положительные, среди всех объектов, которые модель предсказала как положительные. Эта метрика принимает значения от 0 до 1, где 0 означает, что все найденные моделью объекты - ложные срабатывания, а 1 - что всё что нашла модель - правильные объекты.

В нашем случае, это доля объектов, которые модель верно классифицировала как «Books», среди всех объектов, которые она отнесла к классу «Books». Картинка выше наглядно показывает это. 

Формула расчета выглядит следующим образом:

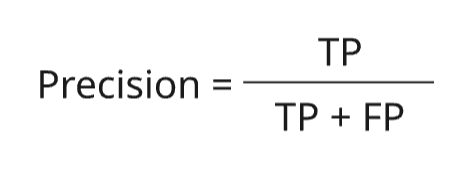
Посчитаем Precision для наших данных

precision = TP / (TP + FP)
print(f"{precision=}")
# precision=0.9417721518987342

и с помощью sklearn

from sklearn.metrics import precision_score
precision_sklearn = precision_score(new_labels_target, new_labels_pred)
print(f"{precision_sklearn=}")
# precision_sklearn=0.9417721518987342

Модель достигает 94% Precision на данных, это говорит о том, что модель редко ошибается, когда относит объект к классу «Books».

Метрику Precision стоит использовать, когда стоимость ложноположительных срабатываний (False Positives) значительно выше, чем стоимость ложноотрицательных. То есть, представим, что в нашем случае, если модель будет относить объект к классу «Books», когда он является не‑«Books» приведет к убытку 1000$, а если модель отнесет не‑«Books» к «Books», ошибка будет стоит 50$.

Таким образом, мы можем допустить чуть больше ложноотрицательных ошибок (False Negatives), чтобы сократить число ложноположительных (False Positives).

Recall

Рассмотрим метрику Recall. Эта метрика показывает, какую долю истинно положительных объектов модель смогла обнаружить из всех имеющихся положительных объектов. Это также хорошо можно увидеть на визуализации выше. Recall принимает значения от 0 до 1, где 0 означает, что модель не нашла ни одного объекта, а 1 - что модель нашла все реальные объекты.

Формула выглядит следующим образом:

Посчитаем Recall для наших данных

recall = TP / (TP + FN)
print(f"{recall=}")
# recall=0.9441624365482234

и с помощью sklearn

from sklearn.metrics import recall_score
recall_score_sklearn = recall_score(new_labels_target, new_labels_pred)
print(f"{recall_score_sklearn=}")
# recall_score_sklearn=0.9441624365482234

Наша модель имеет 94% Recall на тестовых данных,

Метрику Recall стоит использовать в те моменты, когда вам необходимо минимизировать ложноотрицательные срабатывания. Например, если бы модель пропускала класс «Books», то это стоило бы мне 10.000$, а если ошибочно отнесла бы класс «не‑Books» к «Books», это стоило бы 50$.. Соответственно, нам выгодней допустить больше ошибок 2 рода (ошибочно отнести класс «Books» к не‑«Books»).

F1

Это метрика, которая является среднегармоническим между Precision и Recall. Она учитывает обе эти метрики и рассчитывается по формуле:

Эта метрика принимает значение от 0 до 1, где 0 означает, что имеется нулевой Precision или Recall, а 1 - что имеются идеальные Precision и Recall.

Рассчитаем ее для наших данных:

f1 = (2 * precision * recall)/(precision + recall)
print(f"{f1=}")
# f1=0.9429657794676807

Также можно использовать sklearn

from sklearn.metrics import f1_score
f1_sklearn = f1_score(new_labels_target, new_labels_pred)
print(f"{f1_sklearn=}")
# f1_sklearn=0.9429657794676806

Наша модель достигает 94% на F1, что говорит о том, что она демонстрирует достаточно хороший баланс между минимизацией ложноположительных ошибок (FP) и ложноотрицательных ошибок (FN). 

Метрику F1 лучше использовать в те моменты, когда и Precision и Recall одинаково важны, и вам необходимо описать обе эти метрики 1 числом. Эта метрика помогает выявить, есть ли у модели перекос в сторону ложноположительных (FP) или ложноотрицательных (FN) ошибок.

Примечание: отличным приёмом, который можно применять при решении задачи классификации, является улучшение нужных метрик, сдвигая порог принятия решения (то есть, не переобучая модель). Подробнее об этом я рассказал в своём Telegram-канале здесь. Ниже изложу суть кратко. Чаще всего классификатор предсказывает вероятности (логиты) p отношения к классу для объекта. Далее, используя порог (обычно 0.5), объект относится к классу A, если p>=0.5, или к классу B если p<0.5. Соответственно, сдвигая порог 0.5 в большую или меньшую сторону можно регулировать необходимые метрики (precision и recall).

Работа с многоклассовой классификацией

Отлично, мы разобрали основные метрики для бинарной классификации. Однако наш датасет, с которым мы начали работу, имеет 4 класса, на которых мы обучили модель. Как же считаются метрики при таком подходе? 

Для этого можно применять те же метрики, но рассматривать каждый класс отдельно. Именно так мы и делали выше. Мы выбрали класс «Books» и считали все остальные классы как не‑«Books». Далее для каждого класса отдельно считаются метрики. 

Чтобы получать метрики для многоклассовой классификации одним числом, используют усреднение метрики по всем классам. Усреднение бывает нескольких видов:

• Микро‑усреднение — считается следующим образом: для каждого класса считаются TP, FP, TN, FN. Далее происходит суммирование всех TP₁ + TP₂ + ... + TPₙ = SUM_TP (n — количество классов), то же самое и для SUM_FP, SUM_TN, SUM_FN. После этого с полученными SUM_ FP, SUM_TP, SUM_TN, SUM_FN происходит обычный подсчет метрик по вышеуказанным формулам.

• Макро-усреднение — здесь все просто. Для каждого класса считаются Precision, Recall и F1. Далее для каждого класса они усредняются. Пример: (Precision1+Precision2+..PrecisionN)/N (N — количество классов).

• Взвешенное усреднение. При этом подсчёте сначала определяется доля (вес) каждого класса в наборе данных. Вес представляет собой число от 0 до 1, которое считается так: количество объектов класса / количество всех объектов. Затем итоговая метрика вычисляется как средневзвешенное значение метрик каждого класса с учётом этих весов.

Как правильно выбрать необходимый формат усреднения?

Макро‑F1 - используйте, когда все классы одинаково важны, даже если их размеры в данных сильно различаются. Метрика оценивает каждый класс отдельно и усредняет результаты, давая всем классам равный «вес».

Взвешенное F1 - подходит, если набор данных несбалансирован, и вы хотите, чтобы итоговая оценка больше зависела от качества предсказания для крупных классов. Вклад каждого класса в средний результат учитывается пропорционально его размеру.

Микро‑F1 - её целесообразно использовать на сбалансированных данных, когда вам нужна одна общая и интуитивно понятная цифра, описывающая производительность модели в целом, без детализации по классам.

Более подробную информацию по этой теме можно найти здесь.

Отлично, перейдем к практике. Для упрощения подсчетов в sklearn существует функция classification_report, которая автоматически производит подсчет всех необходимых метрик и составляет репорт

from sklearn.metrics import classification_report

print(classification_report(y_test, pred))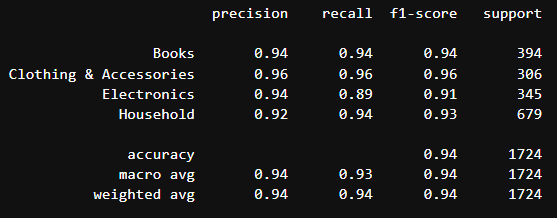

Видим, по каждому классу были рассчитаны Precision, Recall и F1. Также рассчитаны accuracy, macro и micro усреднение по метрикам. Отвечу на возможный вопрос: общая точность (accuracy) в этом отчёте — это и есть микро-усреднение (micro avg). Могли заметить, что оно одно и то же для всех метрик. Это происходит потому, что если вы рассчитаете микро усреднение для всех вышеперечисленных метрик, оно будет одинаково везде (посчитайте и проверьте). По сути, микро-усреднение - это доля правильно классифицированных объектов среди общего числа наблюдений (а это и есть Accuracy).

NER

Рассмотрим тему подсчета метрик для задачи NER. Давайте вспомним, что это за задача:

NER (распознавание именованных сущностей) — это задача поиска и классификации ключевых объектов в тексте. Например, система должна находить имена людей, названия компаний, географические локации или даты. По сути, она отвечает на вопрос: «Что это за объект и где он упоминается в предложении?» (Пример: В предложении «[Иван Петров] работает в [Яндексе]» система выделит имя человека и организацию.)

Возьмем простой пример:

Предложение: Генеральный директор Алексей Иванов улетает в Берлин.

В этом предложении есть 2 сущности: 

• PERSON (PER): Алексей Иванов

• LOCATION (LOC): Берлин. 

Посмотрим, как выглядит NER-разметка для этого предложения

Примечание: В разметке NER по схеме BIO каждый токен (слово) получает тег: B‑ (Beginning) отмечает начало сущности, I‑ (Inside) — её продолжение, а O (Outside) — отсутствие принадлежности к какой-либо сущности.

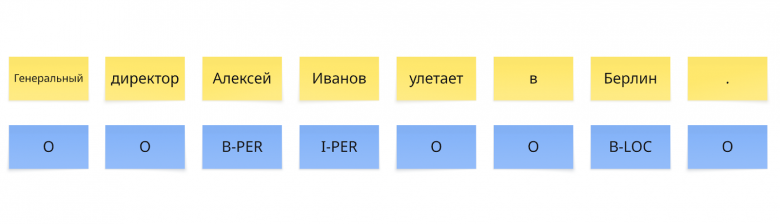
Теперь представим, что мы обучили несколько моделей и получили следующие предсказания

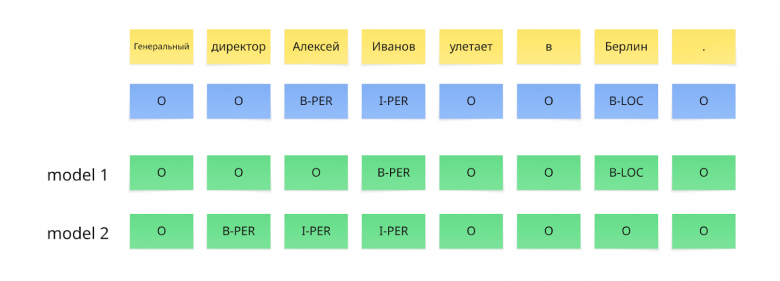
Рассчитаем метрики для Precision, Recall и F1 для каждого из предсказаний. Подсчет метрик в для этой задачи какой‑то степени схож с подходом подсчета метрик в классификации, но в задаче NER учитывается не каждый объект, а целые сущности. 

Проведем подсчет для model 1. В начале необходимо извлечь список сущностей из предложения

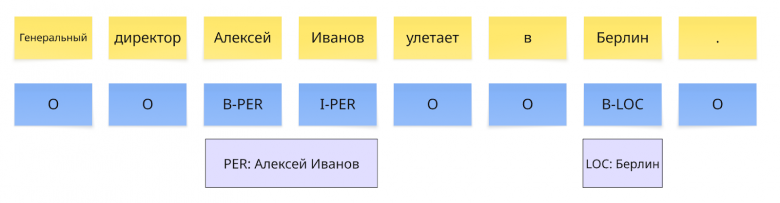
• PER: «Алексей Иванов» (токены 2-3)

• LOC: «Берлин» (токен 6)

Далее извлечем сущности из предсказания model 1

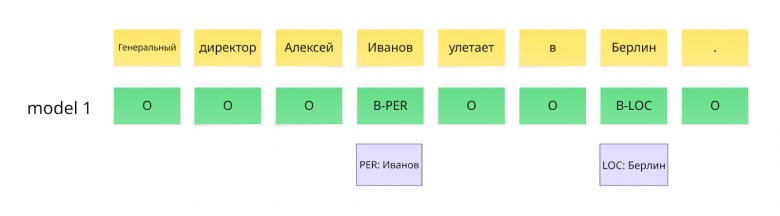
Далее происходит подсчет знакомых нам TP, FP, FN следующим образом: 

Мы сравниваем каждую сущность с предсказаниями:

Сущность PER

Реальная: PER: Алексей Иванов

Предсказанная: PER: Иванов

Получаем следующее:

• FP = 1 (потому что предсказали лишнюю сущность (False Positive))

• FN = 1 (потому что пропустили реальную сущность (False Negative))

Метрики: 

• Precision = TP/(TP+FP)=0/(0+1) = 0

• Recall = TP/(TP+FN)=0/(0+1) = 0 

• F1 = 2*precision*recall/(precision+recall)=2*0*0(0+0) = 0

Сущность LOC

Реальная: LOC: Берлин

Предсказанная: LOC: Берлин

TP=1 (предсказание верное (True Positive))

Метрики: 

• Precision = TP/(TP+FP)=1(1+0) = 1

• Recall = TP/(TP+FN)=1/(1+0) = 1 

• F1 = 2*precision*recall/(precision+recall)=2*1*1/(1+1) = 1

Примечание: вы могли заметить, что не было упомянуто True Negative (TN). Всё правильно, потому что в данном случае мы предсказываем только теги сущностей, а отсутствие тегов (O) модель не предсказывает как отдельный положительный класс. Соответственно, TN всегда равно 0.

Для model 2 считается аналогичным образом.

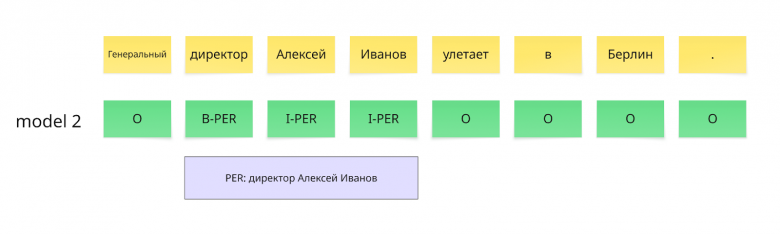
Сущность PER
Реальная: PER: Алексей Иванов

Предсказанная: PER: директор Алексей Иванов

Получаем следующее:

• FP = 1 (предсказали лишнюю сущность)

• FN = 1 (пропустили реальную сущность)

Метрики: 

• Precision = TP/(TP+FP)=0/(0+1) = 0

• Recall = TP/(TP+FN)=0/(0+1) = 0 

• F1 = 2*precision*recall/(precision+recall)=2*0*0(0+0) = 0

Сущность LOC

Реальная: LOC: Берлин

Предсказанная LOC: отсутствует 

• FN = 1 (пропустили реальную сущность)

Метрики: 

• Precision = TP/(TP+FP)=0/(0+0) = 0

• Recall = TP/(TP+FN)=0/(0+1) = 0 

• F1 = 2*precision*recall/(precision+recall)=2*0*0(0+0) = 0

Интерпретировать F1 в данном случае можно так: если F1 = 0, то модель не нашла ни одной сущности правильно, если F1 = 1 - модель нашла все сущности с правильными границами и тегами.

Давайте произведем те же подсчеты на Python. Для подсчета метрик NER существует библиотека seqeval.

from seqeval.metrics import classification_report
from seqeval.scheme import IOB2

# Исходные данные
y_true = [['O', 'O', 'B-PER', 'I-PER', 'O', 'O', 'B-LOC', 'O']]

# Предсказания моделей
y_pred_model1 = [['O', 'O', 'O', 'B-PER', 'O', 'O', 'B-LOC', 'O']]
y_pred_model2 = [['O', 'B-PER', 'I-PER', 'I-PER', 'O', 'O', 'B-LOC', 'O']]

print("=== MODEL 1 ===")
# Подробный отчёт для Model 1
print("\nClassification Report for Model 1:")
print(classification_report(y_true, y_pred_model1, scheme=IOB2))

print("\n\n=== MODEL 2 ===")
# Подробный отчёт для Model 2
print("\nClassification Report for Model 2:")
print(classification_report(y_true, y_pred_model2, scheme=IOB2))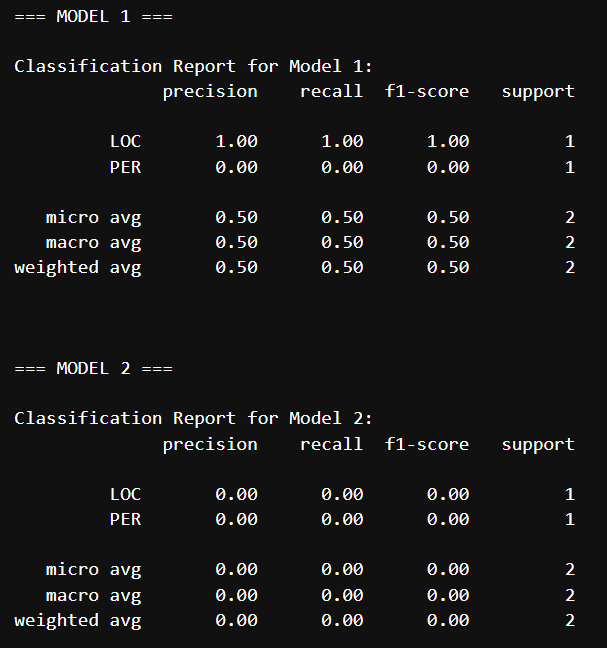

Видим схожий classification report, но уже для NER. 

Таким образом можно считать метрики по предсказаниям для нескольких предложений. Вот небольшой пример, где имеются несколько предложений и несколько предсказаний

from seqeval.metrics import classification_report
from seqeval.scheme import IOB2

y_true = [
    # Пример 1: "Генеральный директор Алексей Иванов улетает в Берлин."
    ['O', 'O', 'B-PER', 'I-PER', 'O', 'O', 'B-LOC', 'O'],
    
    # Пример 2: "Корпорация Apple представила новый iPhone в Калифорнии."
    ['B-ORG', 'I-ORG', 'O', 'O', 'O', 'B-MISC', 'O', 'B-LOC', 'O'],
    
    # Пример 3: "Президент Франции Эммануэль Макрон посетил Берлин и Лондон."
    ['O', 'B-LOC', 'I-LOC', 'B-PER', 'I-PER', 'O', 'B-LOC', 'O', 'B-LOC', 'O']
]


y_pred_model1 = [
    # Пример 1: нашла только фамилию
    ['O', 'O', 'O', 'B-PER', 'O', 'O', 'B-LOC', 'O'],
    
    # Пример 2: не нашла iPhone
    ['B-ORG', 'I-ORG', 'O', 'O', 'O', 'O', 'O', 'B-LOC', 'O'],
    
    # Пример 3: нашла только первого человека и один город
    ['O', 'B-LOC', 'I-LOC', 'B-PER', 'O', 'O', 'B-LOC', 'O', 'O', 'O']
]
print(classification_report(y_true, y_pred_model1, scheme=IOB2))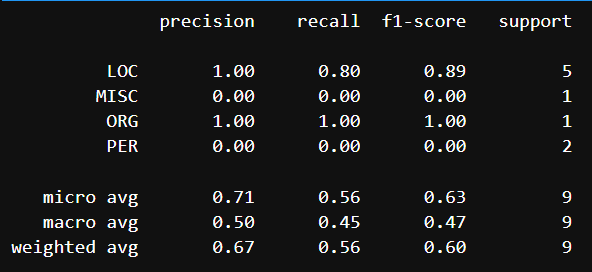

В задаче POS‑теггинга (Part‑of‑Speech tagging) метрики вычисляются на уровне отдельных токенов по аналогии с многоклассовой классификацией. Каждому слову (токену) сопоставляется единственный тег части речи — как в эталонных данных, так и в предсказаниях модели. 

Рассмотрим небольшой пример на Python, в котором рассчитаем знакомые нам метрики для задачи POS.

from sklearn.metrics import classification_report, accuracy_score

# Теги: NOUN - существительное, VERB - глагол, ADJ - прилагательное, PRON - местоимение

y_true = [
    ['NOUN', 'VERB', 'ADJ'],        # Предложение 1
    ['PRON', 'VERB', 'NOUN', 'ADJ'] # Предложение 2
]

y_pred = [
    ['NOUN', 'NOUN', 'ADJ'],        # Ошибка во втором теге
    ['PRON', 'VERB', 'ADJ', 'ADJ']  # Ошибка в третьем теге
]

# "Сглаживаем" списки для оценки
y_true_flat = [tag for sentence in y_true for tag in sentence]
y_pred_flat = [tag for sentence in y_pred for tag in sentence]

print(classification_report(y_true_flat, y_pred_flat))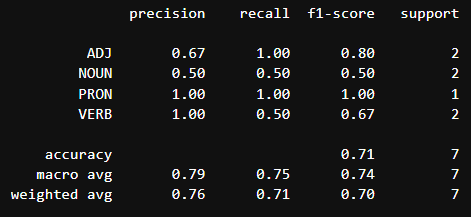

Кластеризация

Для начала вспомним, что такое кластеризация. Решая задачу кластеризации, необходимо разбить множество объектов на подмножества на основе общих признаков. Это задача обучения без учителя. То есть, для разделения объектов на подмножества используется информация и закономерности в данных.

Для оценки кластеризации используют два вида метрик: внутренние и внешние.

Ниже мы рассмотрим примеры расчета обоих типов метрик на синтетических примерах, а потом попробуем сделать то же самое для датасета товаров, о которых говорилось выше.

Внешние метрики

Начнем с внешних метрик. 

Данный вид метрик считается, если нам заранее известны метки классов для объектов. На основе них мы можем понять, хорошо ли модель кластеризует объекты на подгруппы. Существует множество «внешних» метрик для кластеризации: Rand Index, Mutual Information, V‑measure и так далее В качестве понятного примера мы рассмотрим метрику Rand Index.

Rand Index (RI)

Это метрика, которая показывает сходство между кластерами, путем попарного сравнения. Рассмотрим пример. 

Представим, что мы имеем наборы кластеризованных данных моделью и реальные метки кластеров.

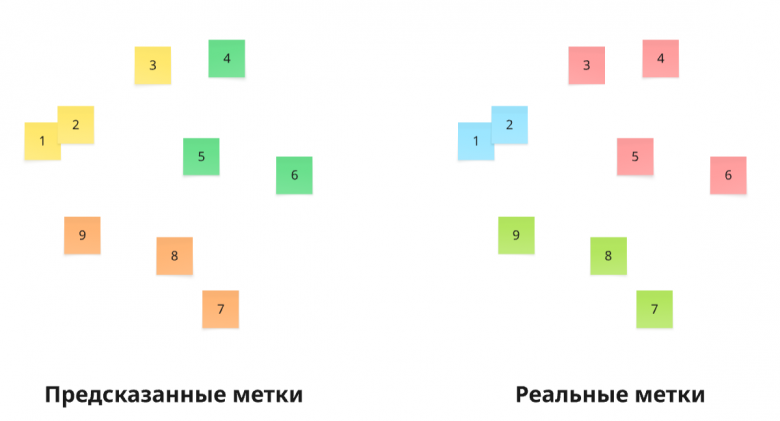
На основе этих множеств мы можем подсчитать привычную нам матрицу ошибок. Подсчет этой матрицу будет отличаться от подхода, используемого в задаче классификации. А именно, представим представленные метки в виде двух множеств:

# использую разные числа в обоих массивах, чтобы показать, что нам важна именно группа, в которой находится объект, а не сам класс.
predicted_labels = [0, 0, 0, 1, 1, 1, 2, 2, 2]
target_labels = [1, 1, 2, 2, 2, 2, 3, 3, 3]

Для расчета матрицы ошибок (TP, TN, FP, FN) в задаче кластеризации используется попарное сравнение всех объектов (всех возможных комбинаций пар). Сравниваются не сами метки, а факт нахождения двух объектов в одном кластере или в разных в двух разбиениях — предсказанном и истинном.

Логика подсчета:

• TP (True Positive): Пара объектов находится в одном кластере и в предсказании, и в истинном разбиении.

• TN (True Negative): Пара объектов находится в разных кластерах и в предсказании, и в истинном разбиении.

• FP (False Positive): Пара объектов находится в одном кластере в предсказании, но в разных в истинном разбиении.

• FN (False Negative): Пара объектов находится в разных кластерах в предсказании, но в одном в истинном разбиении.

Реализуем вышесказанное на Python

from itertools import combinations

predicted_labels = [0, 0, 0, 1, 1, 1, 2, 2, 2]
target_labels = [1, 1, 2, 2, 2, 2, 3, 3, 3]

# Инициализация счетчиков
TP = TN = FP = FN = 0

# Получаем все уникальные пары индексов (0,1), (0,2), ... (7,8)
all_pairs = list(combinations(range(len(predicted_labels)), 2))

for i, j in all_pairs:
    # Сравнение в предсказанном разбиении
    same_pred = (predicted_labels[i] == predicted_labels[j])
    # Сравнение в истинном разбиении
    same_true = (target_labels[i] == target_labels[j])
    
    # Классификация пары на основе логики, описанной выше
    if same_true and same_pred:
        TP += 1
    elif not same_true and not same_pred:
        TN += 1
    elif not same_true and same_pred:
        FP += 1
    else: # same_true and not same_pred
        FN += 1

print(f"TP = {TP}, TN = {TN}, FP = {FP}, FN = {FN}")
# TP = 7, TN = 24, FP = 2, FN = 3

После подсчета матрицы ошибок, происходит вычисление метрики Rand Index. Формула метрики выглядит следующим образом:

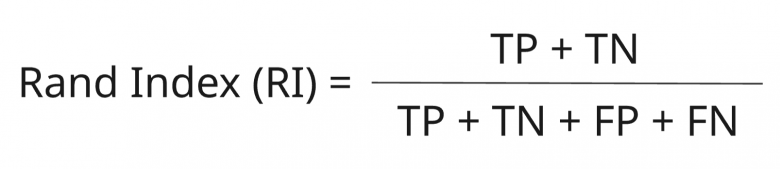
Эта метрика измеряется от 0 до 1, где 0 означает, что кластеризация произведена наихудшим способом, а 1 - кластеры предсказаны полностью верно.

RI = (TP + TN) / (TP + TN + FP + FN)
print(f"Rand Index = {RI:.4f}") 
# Rand Index = 0.8611

Для упрощения подсчета в sklearn существует функция для подсчета RI 

from sklearn.metrics.cluster import rand_score
RI_sklearn = rand_score(predicted_labels, target_labels)
print(f"Rand Index sklearn = {RI_sklearn:.4f}") 
# Rand Index = 0.8611

Обычный индекс Рэнда (RI) может давать завышенные значения даже при случайном разбиении данных, так как учитывает большое количество пар объектов, которые и так находятся в разных кластерах (TN). Чтобы устранить это смещение и сделать метрику более строгой, используется скорректированный индекс Рэнда (ARI) — он вычитает ожидаемое значение RI при случайной кластеризации и показывает, насколько результат лучше случайного угадывания. 

Для расчета ARI в sklearn также существует функция adjusted_rand_score

from sklearn.metrics import adjusted_rand_score
ARI_sklearn = adjusted_rand_score(predicted_labels, target_labels)
print(f"Adjusted Rand Index sklearn = {ARI_sklearn:.4f}") 
# Adjusted Rand Index sklearn = 0.6429

Rand Index - простая для понимания метрика, с помощью которой можно понять, насколько хорошо модель способна разбивать объекты на кластеры. Ее стоит использовать в тех случаях, когда нужна простая в понимании метрика для оценки модели кластеризации. Её не используют, если реальные метки кластеров неизвестны. 

Внутренние метрики

Это метрики, которые не требуют наличия правильных меток кластеров для объектов. Они используют внутренние свойства данных и кластеризованных объектов для оценки качества кластеризации. Существуют различные внутренние метрики кластеризации: Silhouette Coefficient, Calinski‑Harabasz Index, Davies‑Bouldin Index. В качестве примера мы рассмотрим расчёт популярной метрики Silhouette Coefficient (или коэффициент силуэта).

Коэффициент силуэта

Это метрика, которая позволяет оценить качество кластеризации, посредством оценки схожести объектов в кластерах. А именно, данная метрика показывает, насколько объекты в одном кластере похожи на друг на друга, и насколько они отличаются от объектов в других кластерах. Рассмотрим простой пример расчета.

Наилучшее значение коэффициента силуэта равно 1, а наихудшее — -1. Значения близкие к 1 обозначают, что объект соответствует своему кластеру и сильно отличается от других, значения близкие к -1 обозначают, что объект ближе к другим кластерам, чем к своему. Если значение близко к 0, это означает, что объект находится в пересечении кластеров, что говорит о наличии перекрытия кластеров друг с другом.

Представим, что мы имеем набор объектов, расположенных на координатной плоскости. Далее мы провели кластеризацию при помощи определенной модели (например KMeans) и получили кластеры.

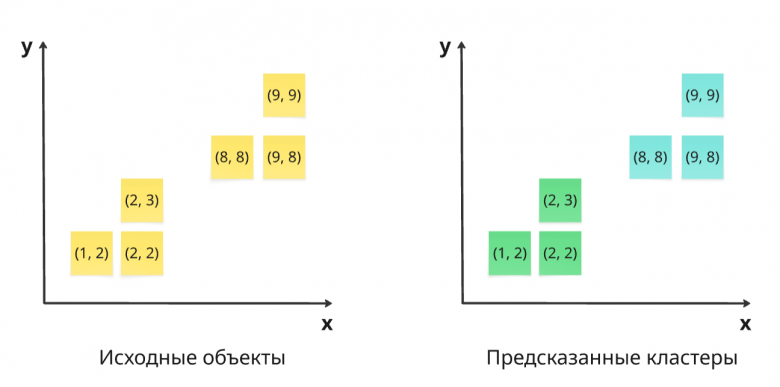
Получили 2 кластера. Посчитаем коэффициент силуэта по этому разбиению на Python.

X = np.array([
    [1, 2], [1, 3], [2, 2],  # Кластер 0
    [8, 8], [9, 8], [9, 9]   # Кластер 1
])

# Метки кластеров
labels = np.array([0, 0, 0, 1, 1, 1])

Сначала рассчитывается внутрикластерное расстояние aᵢ, которое представляет собой среднее расстояние от точки до всех других точек её же кластера. Чем меньше это значение, тем компактнее кластер и тем ближе точка к своим соседям по группе.

def calculate_a_i(i, data, labels):
    """Расчет внутрикластерного расстояния для точки i"""
    # Получаем метку кластера текущей точки
    current_label = labels[i]
    
    # Находим индексы всех точек того же кластера
    same_cluster_indices = np.where(labels == current_label)[0]
    
    # Удаляем саму точку i из списка
    same_cluster_indices = same_cluster_indices[same_cluster_indices != i]
    
    # Если в кластере только одна точка, возвращаем 0
    if len(same_cluster_indices) == 0:
        return 0.0
    
    # Вычисляем расстояния до всех точек своего кластера
    distances = []
    for j in same_cluster_indices:
        # Евклидово расстояние между точками i и j
        distance = np.sqrt(np.sum((data[i] - data[j]) ** 2))
        distances.append(distance)
    
    # Возвращаем среднее расстояние
    return np.mean(distances)

Затем вычисляется межкластерное расстояние bᵢ — это минимальное среднее расстояние от рассматриваемой точки до любого другого кластера. Здесь мы для каждого чужого кластера находим среднее расстояние до всех его точек и выбираем наименьшее значение. Чем больше bᵢ, тем дальше точка от соседних кластеров, что свидетельствует о хорошем разделении между группами.

def calculate_b_i(i, data, labels):
    """Расчет расстояния до ближайшего чужого кластера для точки i"""
    # Получаем метку кластера текущей точки
    current_label = labels[i]
    
    # Получаем все уникальные метки кластеров
    unique_labels = np.unique(labels)
    
    # Список для хранения средних расстояний до других кластеров
    avg_distances = []
    
    # Перебираем все кластеры, кроме своего
    for label in unique_labels:
        if label == current_label:
            continue
        
        # Находим точки другого кластера
        other_cluster_indices = np.where(labels == label)[0]
        
        # Вычисляем расстояния до всех точек этого кластера
        distances = []
        for j in other_cluster_indices:
            distance = np.sqrt(np.sum((data[i] - data[j]) ** 2))
            distances.append(distance)
        
        # Среднее расстояние до этого кластера
        avg_distances.append(np.mean(distances))
    
    # Возвращаем минимальное среднее расстояние (ближайший чужой кластер)
    return min(avg_distances)

На основе этих двух значений рассчитывается силуэт для точки по формуле sᵢ = (bᵢ — aᵢ) / max(aᵢ, bᵢ). Результат интерпретируется следующим образом: значения близкие к 1 указывают на отличное соответствие точки своему кластеру, около 0 — на нахождение на границе кластеров, а отрицательные значения — на возможную ошибку в кластеризации. Общий силуэт, представляющий собой среднее значение силуэтов всех точек, дает интегральную оценку качества разбиения данных на кластеры.

def calculate_silhouette(i, data, labels):
    """Расчет силуэта для одной точки"""
    a_i = calculate_a_i(i, data, labels)
    b_i = calculate_b_i(i, data, labels)
    
    # Если a_i и b_i оба равны 0 (например, кластер из одной точки)
    if a_i == 0 and b_i == 0:
        return 0.0
    
    # Расчет силуэта по формуле: (b_i - a_i) / max(a_i, b_i)
    return (b_i - a_i) / max(a_i, b_i)

def calculate_overall_silhouette(data, labels):
    """Расчет общего силуэта для всех точек"""
    silhouette_scores = []
    
    for i in range(len(data)):
        s_i = calculate_silhouette(i, data, labels)
        silhouette_scores.append(s_i)
    
    # Общий силуэт - среднее значение по всем точкам
    return np.mean(silhouette_scores)

# Расчет силуэта для точки 0
s_i = calculate_silhouette(0, data, labels)
print(f"Силуэт для точки 0: {s_i:.3f}")
# Вывод: Силуэт для точки 0: 0.879

# Расчет общего силуэта
overall_silhouette = calculate_overall_silhouette(data, labels)
print(f"Общий силуэт: {overall_silhouette:.3f}")
# Общий силуэт: 0.880

Для упрощение, в sklearn имеется функция для расчета силуэта.

from sklearn.metrics import silhouette_score
sklearn_score = silhouette_score(data, labels)
print(f"Силуэт sklearn: {sklearn_score:.3f}")
# Силуэт sklearn: 0.880

Расчет метрик на собственных данных

Проведем расчет вышеперечисленных метрик для нашего датасета с товарами. Воспользуемся теми же векторами, которые мы рассчитывали для задачи классификации.

import numpy as np
import pandas as pd

df_train = pd.read_excel("./train_data.xlsx")
embeddings_train = np.load("./train_embed.npy")

Визуализируем кластеры, используя алгоритмы PCA и t‑SNE, используя эмбеддинги и известные метки классов

# Получаем уникальные категории
unique_categories = df_train['category'].unique()
num_categories = len(unique_categories)

colors = ['red', 'blue', 'green', 'purple']

# PCA
pca = PCA(n_components=2, random_state=42)
embeddings_2d_pca = pca.fit_transform(embeddings_train)

# t-SNE
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
embeddings_2d_tsne = tsne.fit_transform(embeddings_train)

# Создаем графики
fig, axes = plt.subplots(1, 2, figsize=(16, 7))

# PCA график
for i, category in enumerate(unique_categories):
    mask = df_train['category'] == category
    axes[0].scatter(embeddings_2d_pca[mask, 0], 
                    embeddings_2d_pca[mask, 1], 
                    c=colors[i], 
                    label=category, 
                    alpha=0.5, 
                    s=30,
                    edgecolors='w',
                    linewidth=0.5)

axes[0].set_title('PCA: Распределение по категориям', fontsize=14, fontweight='bold')
axes[0].set_xlabel('Component 1')
axes[0].set_ylabel('Component 2')
axes[0].legend(title='Категории', fontsize=10, title_fontsize=11)
axes[0].grid(True, alpha=0.3)

# t-SNE график
for i, category in enumerate(unique_categories):
    mask = df_train['category'] == category
    axes[1].scatter(embeddings_2d_tsne[mask, 0], 
                    embeddings_2d_tsne[mask, 1], 
                    c=colors[i], 
                    label=category, 
                    alpha=0.5, 
                    s=30,
                    edgecolors='w',
                    linewidth=0.5)

axes[1].set_title('t-SNE: Распределение по категориям', fontsize=14, fontweight='bold')
axes[1].set_xlabel('Dimension 1')
axes[1].set_ylabel('Dimension 2')
axes[1].legend(title='Категории', fontsize=10, title_fontsize=11)
axes[1].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()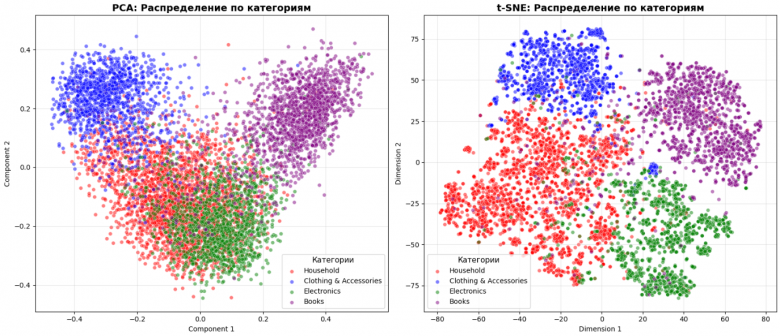

Видим, что используя t‑SNE хорошо выделяются 4 кластера по каждой категории товаров. Видим, что имеется частичное пересечении категорий Electronics и Household.

Далее кластеризуем данные, используя модель кластеризации KMeans.

from sklearn.cluster import KMeans
# Указываем 4 кластера, так как заранее знаем что категорий 4
kmeans = KMeans(n_clusters=4).fit(embeddings_train)
draw_pca_t_sne(data=embeddings_train, labels=kmeans.labels_)

Визуально можем увидеть, что алгоритм достаточно хорошо разделяет наши объекты на кластеры. 

Теперь посчитаем метрики кластеризации, о которых говорили выше. 

Rand Index:

from sklearn.metrics import rand_score, adjusted_rand_score

RI = rand_score(pred_labels, target_labels)
ARI = adjusted_rand_score(pred_labels, target_labels)

print(f"RI={RI}")
print(f"ARI={ARI}")
# RI=0.8671868986128088
# ARI=0.6631282084154457

Видим неплохую RI для нашей модели кластеризации.

Далее посчитаем коэффициент силуэта 

from sklearn.metrics import silhouette_score

SS = silhouette_score(embeddings_train, pred_labels)

print(f"silhouette_score={SS}")
# silhouette_score=0.04977119341492653

Видим значение, близко к нулю, что говорит о наличии перекрывающих кластеров (это и видно на визуализации выше).

Заключение

В этой статье мы рассмотрели метрики для задач классификации, NER и кластеризации. В следующих частях будут рассмотрены метрики для задач генерации текста, перевода, RAG и другие. 

Подписывайтесь на мой Telegram-канал, в котором я также рассказываю интересные вещи об IT и AI технологиях.