Доброго времени суток.
А знаете ли вы, что не все хеш таблицы одинаково полезны? Сейчас я расскажу вам историю, как одна плохая хеш таблица скушала всю производительность, и не поморщилась. И как исправление этой хеш таблицы ускорило код почти в 10 раз.
Конечно, согласно теме — в статье речь пойдет о Delphi, но даже если вы не Delphi разработчик, то все равно советую заглянуть под кат, а после прочтения статьи в исходный код хеш таблиц, которые вы используете. А Delphi разработчикам я советую вообще отказаться от стандартного TDictionary.

1. Как устроена хеш таблица.

Если вы отлично знаете как устроена хеш таблица, и что такое linear probing — можете смело переходить ко второй части.

Любая хеш таблица внутри — это по сути некоторый массив. Элементы такого массива принято называть bucket-ами. И одно из центральных мест в хеш таблице — это хеш функция. Вообще хеш функция — это функция, отображающее одно множество на другое множество фиксированного размера. И задача любой хеш функции — дать равномерно распределенный результат на фиксированном множестве. Больше о хеш функциях можно почитать в википедии, я не буду на этом останавливаться.
Итак мы подготовили массив из скажем 10 bucket-ов. Теперь мы готовы складывать значения в наш массив. Мы берем хеш от нашего ключа. Например хеш оказался 32 битным целым числом M. Чтобы определить, в какой bucket мы будем записывать наше значение — мы берем остаток от деления: Index := M mod 10. И кладем в bucket[Index] := NewKeyValuePair.
Рано или поздно мы столкнемся с тем, что в bucket[Index] уже будет лежать какое-то значение. И нам нужно будет что-то с этим делать. Такой случай называется разрешением коллизий (Collision resolution). Существует несколько техник разрешения коллизий. Вот основные:

Separate chaining или closed addressing

В простейшем случае этот метод представляет вот что. Каждый bucket — это ссылка на голову связанного списка (linked list). Когда возникает коллизия — мы просто добавляем в linked list еще один элемент. Чтобы наш список не выродился в несколько линейных linked list-ов вводят такое понятие как load factor. То есть когда количество элементов на один bucket превышает некоторое число (load factor) — создается новый массив bucket-ов, и все элементы из старого распихиваются по новым. Процедура называется rehash.
Недостатки этого подхода в том, что для каждой пары <ключ, значение> мы создаем объект, который надо добавить в linked list.
Этот подход можно улучшить. Например если вместо bucket-ов хранить пару <ключ, значение> + ссылку на голову linked list-а. Установив load factor в 1 или даже 0.75 можно практически избежать создания элементов linked list-а. А bucket-ы, которые есть массив — очень дружелюбно кладутся на кеш процессора. p.s. На данный момент я считаю это лучшим способом разрешения коллизий.

Open addressing

Для этого метода у нас все bucket-ы — это массив <ключ, значение>, и абсолютно все элементы хеш таблицы хранятся в bucket-ах. По одному элементу на bucket. Попытка вставить элемент в такую хеш таблицу называется probe. Наиболее известны такие методы проб: Linear probing, Quadratic probing, Double hashing.
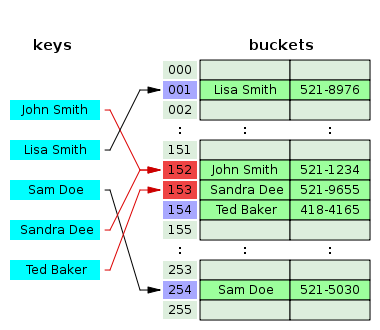
Давайте посмотрим как работает Linear probing.
Вот мы попали в ситуацию, когда bucket уже занят другим элементом:

Тогда мы просто прибавляем к bucket-у единицу, и кладем элемент в соседний:

Снова попали в этот же bucket? Теперь придется перешагнуть аж 3 элемента:

А вот совсем неудачно получилось:

По последнему примеру хорошо видно, что для того, чтобы данный метод был эффективен — нужно чтобы было много свободных bucket-ов, а еще очень важно, чтобы вставляемые элементы не кучковались в определенных участках, что накладывает высокие требования на хеш функцию.
Попытка обойти неудачную хеш функцию — это Quadratic probing и Double hashing. Суть Quadratic probing в том, что следующая probe будет через 1, 2, 4, 8 и т.д. элементов. Суть Double hashing в том, что размер прыжка для следующей probe выбирается с помощью хеш функции. Либо отличной от первой, либо той же, но хеш берется от индекса bucket в который только что пытались положить.
Но самое главное в Open addressing то, что даже если мы 10000 элементов заполнили без единой коллизии, то добавление 10001-го может привести к тому, что мы переберем все 10000 уже находящихся там элементов. И самое страшное, что когда мы положим этот 10001-ый, чтобы потом к нему обратиться — нам опять придется перебрать 10000 предыдущих.
Есть еще одна неприятная вещь, которая следует из всего вышесказанного. Для Open addressing важен порядок заполнения. Какая бы замечательная хешфункция не была все может испортить порядок заполнения. Давайте рассмотрим последний случай, нам не повезло. Все элементы были заполнены без единой коллизии, но последний элемент с коллизией, которая привела к перебору кучи bucket-ов:

А что если бы мы сначала положили этот единственный элемент:

у нас коллизия, мы перебрали всего 1 бакет.
А потом положили бы соседа:

снова перебрали бы 1 бакет.
И следующего соседа:

В сумме добавление бы привело всего к одной коллизии на каждый элемент. И хотя суммарное кол-во перебранных bucket-ов при добавлении осталось бы прежним — оно в целом стало бы более сбалансированным. И теперь при обращении к любому элементу мы бы сделали 2 проверки в bucket-ах.

2. Так что же не так в Delphi с Linear probing в TDictionary?

Ведь такой «неудачный» порядок с хорошей хешфункцией сложно получить, скажете вы? И сильно ошибетесь.
Для того, чтобы получить все элементы TDictionary — нам надо пройтись по массиву бакетов, и собрать элементы в занятых ячейках. Главный подвох тут в том, что последовательность сохраняется! Просто создаем еще один TDictionary, и перекидываем данные в него… и получаем кучу коллизий на последних элементах перед очередным grow.
Простейший код, чтобы воспроизвести ситуацию:

    Hash1 := TDictionary<Integer, Integer>.Create();
    Hash2 := TDictionary<Integer, Integer>.Create();

    for i := 0 to 1280000 do // этот TDictionary заполнится очень быстро
        Hash1.Add(i, i);
    for i in Hash1.Keys do // а этот - неожиданно медленнее, в десятки раз!
        Hash2.Add(i, i);

В TDictionary rehash наступает только тогда, когда свободных ячеек в массиве bucket-ов становится меньше 25% (Grow threshold = 75%). Увеличение емкости происходит всегда в 2 раза. Вот заполненные bucket-ы в большом словаре:

попытка добавить данные элементы в таблицу меньшего размера можно рассмотреть так. Разделим большую таблицу на 2 части. Первая часть ляжет абсолютно идентично.

Теперь нам надо добавить элементы из второй половины (зелененькие).

Видите как растет число коллизий при добавлении второй половины? И если до rehash-а еще далеко, а таблица достаточно большая — мы можем получить колоссальный оверхед.
Давайте посчитаем кол-во коллизий при добавлении нового элемента. Для этого я скопировал себе исходный код TDictionary, и добавил пару коллбек методов, возвращающих коллизии. Результаты вывел на графики:

Я заполнял хеш таблицу значениями, и по мере заполнения измерял количество коллизий, каждые новые N значений отображает новый пиксель по оси X. Т.е. горизонтальная ось отображает заполнение таблицы, а вертикальная — количество коллизий. Справа от каждого графика значения:

• Max collision — максимальное количество коллизий в пределах одного пикселя по оси X.
• Items per pixel — количество элементов, приходящихся на один пиксель графика по оси X.
• Items count — суммарное кол-во элементов в хештаблице
• Filling percentage — отношение кол-ва элементов к количеству bucket-ов в таблице.

Черная линия — максимальное число коллизий в пикселе. Красная — среднее арифметическое от коллизий в пикселе.
На первом графике при заполнении 48% все хорошо. Максимум коллизий 169. Как только мы перешагиваем 50% — начинается самая жуть. Так при 61% наступает самая жость. Количество коллизий на элемент может достигать 130 тысяч! И так до 75%. После 75% происходит grow, и процент заполнения уменьшается.
Каждая пила с кучей коллизий — ничто иное, как то, что я показывал на рисунке выше. Заканчивается «пила» rehash-ом и резким падением коллизий.
Волей случая вы можете оказаться на верху такой пилы, и попытка работать с последними добавленными элементами будет сопровождаться у вас сильными тормозами.
Как же это исправить? Ну самый очевидный вариант — это grow threshold установить в 50%. Т.е. свободных ячеек в хештаблице должно быть не менее 50%. Изменение этого порога дает вот такие графики:

на тех же объемах данных. Ценой дополнительной памяти мы «выйграли» себе процессорное время. Проблема тут в том, что поле GrowThreshold недоступно снаружи. Можно так же постараться избежать неудачных последовательностей. Либо вручную перемешивать/сортировать данные перед помещением в таблицу, что достаточно накладно, либо создавать разные таблицы с разными хешфункциями. Многие хешфункции (такие как Murmur2, BobJenkins hash) дают возможность задать Seed/InitialValue. Но эти значения наобум подбирать тоже не рекомендуется. В большинстве случаев в качестве seed подойдет простое число, но все таки лучше почитать мануал по конкретной хеш функции.
Ну и наконец мой совет — не используйте Open addressing как универсальный метод для любой хеш таблицы. Я считаю лучше обратить внимание на Separate chaining с бакетами <ключ, зачение>+указатель на голову linked list-а с load factor-ом около 0.75.

p.s. На поиск данного подводного камня я потратил несколько дней. Ситуация осложнялась тем, что большие объемы данных отпрофайлить сложно + зависимость от % заполнения TDictionary приводила к тому, что тормоза мистическим образом периодически пропадали. Так что спасибо за внимание, и надеюсь вы об это не споткнетесь. ;)