
Ниже речь пойдёт о старушке рекурсии, которую неплохо бы представлять, понимать и применять.
Примечание: Данная небольшая статья написана для беглого ознакомления с рекурсией, некоторыми примерами её применения и опасностями.
Определение
Для начала стоит сказать, что рекурсия относится не только к программированию. Рекурсия — это общее понятие, которое может быть присуще чему угодно и встречаться в повседневной жизни, но больше всего она распространена в информатике и математике. Для программистов же умение применять рекурсию — большой плюс в коллекцию полезных навыков.
Самая большая глупость — это делать то же самое и надеяться на другой результат.
Под рекурсией понимают процесс повторения элементов самоподобным образом. Объект обладает рекурсией, если он является частью самого себя.
Частным случаем рекурсии является хвостовая рекурсия. Если любой рекурсивный вызов является последней операцией перед возвратом из функции, то это оно.
Некоторые примеры
Рекурсию надо бы понять, а определение для этого подходит хуже, чем наглядные примеры. Для лучшего понимания, конечно, всё же следует прочитать определение, посмотреть на пример, снова прочитать определение и снова посмотреть на пример… Повторять, пока не придёт осознание.
Отличный пример вы можете найти тут.
Самое известное программисту применение рекурсии — задачи на вычисление чисел Фибоначчи или факториала. Давайте покажем, как это реализовать на языке C:
int fib(int n) {
if (n == 0) return 0;
if (n == 1 || n == 2) return 1;
return fib(n - 1) + fib(n - 2);
} fib(1,1):-!.
fib(2,1):-!.
fib(N,R):-
N1 is N-1, fib(N1, R1),
N2 is N-2, fib(N2, R2),
R is R1 + R2.Тут же стоит отметить, что декларативная парадигма, в частности парадигма логического программирования, намного лучше позволяет понять рекурсию, так как там это обычное дело.
int factorial_rec(int n, int res) {
if (n == 0) return res;
return factorial_rec(n - 1, res * n);
}
int factorial(int n) {
return factorial_rec(n, 1);
}Fork-бомба
Примечание: Рекурсивное создание процессов крайне быстро (из-за экспоненциального роста их количества) заполняет таблицу процессов, что достаточно опасно для системы.
#include <unistd.h>
int main() {
while(true) fork();
}Reboot кнопкой после такого делать немного не приятно.
Для математика первой ассоциацией, скорее всего, будет фрактал. Фракталы прекрасны и приятно для глаза показывают свойства самоподобия.
Самые известные фракталы:
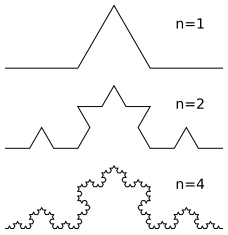


Ну и в повседневной жизни классическим примером являются два зеркала, поставленных друг напротив друга.
Углубимся глубже

Проста ли рекурсия? Однозначно нет. На вид кажется, что всё просто, однако рекурсия таит в себе опасности (А иногда она просто не понятна).
Вернёмся к примеру с вычислением чисел Фибоначчи. Сразу заметим, что возвращаемым результатом функции является вызов этой же функции, а если быть точнее, то сумма результатов вызова двух функций (именно поэтому рекурсия не хвостовая). Становится понятно, что второй вызов не произойдёт, пока не завершится первый (в котором также будет вызов двух функций). Тут же пытливый ум заметит, что из рекурсивной функции должен существовать "нормальный" выход, без самовызова, иначе мы познакомимся с переполнением стека вызовов — это один из ключевых моментов, который стоит держать в голове при работе с функциями вызывающими сами себя.
Заметим, что дерево вызовов получится большим, но максимальное количество вызовов в стеке будет заметно меньше (N-1 при N > 2, соответственно).

Рекурсивные алгоритмы довольно-таки часто встречаются при работе с деревьями, сортировками и задачами на графах. Так что, чтобы лучше вникнуть нужна практика и для этого не плохо подходит вышеупомянутое (в частности, бинарные или общие деревья. Их реализация не так сложна, а опыт работы с рекурсией получится не плохой).
Помимо этого хотелось бы упомянуть Ханойские башни, которые также отлично подойдут для ознакомления с рекурсивными задачами. На Хабре также был отличный разбор этой игры.
Для полноты картины обязательно надо упомянуть о борьбе с рекурсией.
Зачем же с ней бороться?
Повышается производительность. Но это не значит, что с ней просто необходимо бороться, ведь применение рекурсии очевиднее, проще и приятнее, чем итерационные варианты.
Под силу ли побороть любую рекурсию?
Однозначно да. Любой рекурсивный алгоритм можно переписать без использования рекурсии, а хвостовую рекурсию же очень легко перевести на итерацию (чем и занимаются некоторые компиляторы для оптимизации). Это также относится и к итерационным алгоритмам.
Самый известный способ — это использование стека. Здесь подробнее, для интересующихся.
Заключение
Спасибо за прочтение статьи. Надеюсь, что большинство не знакомых с рекурсией получили базовое представление о ней, а от знающих людей, конечно, хочется услышать дополнения и замечания в комментариях. Не бойтесь рекурсии и не переполняйте стек!
UPD: Добавлен корректный пример хвостовой рекурсии.
Комментарии (34)

SbWereWolf
17.01.2017 23:46-1Под силу ли побороть любую рекурсию?
не рекурсивный обход графа? не рекурсивный поиск пути? наверное можно, но как то сложно это :) с рекурсией проще
lair
18.01.2017 00:01+2не рекурсивный обход графа?
А в чем проблема? И BFS, и DFS есть в нерекурсивных вариантах.
не рекурсивный поиск пути?
Алгоритмы Дийкстры, Беллмана-Форда, Флойд-Уоршелла и Джонсона — нерекурсивные.
Когда графы большие, рекурсивные алгоритмы просто не справляются из-за глубины стека.

Saffron
17.01.2017 23:46Вы привели много примеров рекурсии, и ни одного определения.

KvanTTT
18.01.2017 03:01Чтобы понять рекурсию нужно понять рекурсию...

Saffron
18.01.2017 03:13+3Не всякая фраза, удовлетворяющая грамматике, имеет смысл. Мы ведь не сможете представить треугольник с четырьмя углами и пятью рёбрами. Хотя по отдельности, треугольники, углы, рёбра существуют, да и числительные тоже бывают. Множество всех множеств — такой же парадокс, где за простыми словами скрыта невозможная концепция.
Впрочем, про ваше утверждение этого не скажешь. Оно абсолютно корректно, ибо является тавтологией. Но не на дюйм не приближает к пониманию рекурсии.
loginsin
18.01.2017 06:22+4Надо отметить, что весь пост можно сократить до вышеозначенной фразы. В нем не содержится ничего такого, что помогло бы в будущем принять решение о применении рекурсии. Чего стоит только ответ на вопрос «Зачем же с ней бороться?». Из ответа понятно чуть меньше, чем ничего.
В свое время (очень давно) проходил собеседование, кажется в ABBYY, и там дали задачку по вычислению результата функции вроде f(xn)=z(f(xn-1)), где z — еще какая-то функция (не помню какая). Естественно, я подошел к решению с помощью рекурсии. И естественно, я был не первый такой умник, судя по ухмылке интервьюера. Довольно наглядно и на пальцах показал, что человечество еще не подошло к созданию таких вычислительных машин, чтобы вычислить с помощью рекурсии значение функции даже для f(5) в разумные пределы времени с разумным количеством памяти, несмотря на то, что результат вычисления находился в пределах от 1 до 100.
К чему я это? Опытный взгляд увидит из картинки автора, что f(0) вычисляется 5 раз, f(1) уже 8 раз, f(2) тоже 5 раз. Да, для f(0), f(1), f(2) вычислений почти не производится, но для f(100) что будет? И что будет, если это не вычисление Фибоначчи, а что посложнее?
Пост был бы намного богаче в смысловом плане, если бы давал представления о применимости рекурсии. Лично для меня никогда не было понятно применение рекурсии для вычисления факториала или тех же чисел Фибоначчи с диким оверхедом, если это делается намного нагляднее банальным циклом. При этом рекурсия вполне разумно подходит для поиска файлов. Но из текста поста этого ничего не ясно: бороться с ней нужно, но необязательно; бороться можно, но непонятно как.
IIvana
18.01.2017 07:01И что будет, если это не вычисление Фибоначчи, а что посложнее?
Что будет, зависит от того, кто делает. Например, банальная мемоизация результатов чистых функций спасет отца русской демократии (да, я в курсе про переполнение инта):
int a[100]; int f(int i) { if (i<2) return i; else { if (a[i]==0) a[i]=f(i-1)+f(i-2); return a[i]; } } int main() { std::cout << f(100); }
В свое время, решая многочисленные задачки типа размена монет и подсчета вариантов, я быстро находил тривиальные лобовые экспоненциально-рекурсивные решения, которые тормозили на определенных объемах данных. И было 2 пути — либо каждый раз придумывать свой отдельный другой алгоритм именно для этой конкретной задачи (что любят называть термином динамическое программирование, хотя кое-кто (и я в том числе) причисляют к этому и рекурсию с мемоизацией), либо один раз и навсегда написать абстракцию универсального мемоизатора, и скармливать ему любые тривиально рекурсивные схемы. Даже кату по этому поводу создал — https://www.codewars.com/kata/550756a881b8bdba99000348 Хотя если мы дошли до ФП, и Хаскеля в частности, то это отдельнаяпеснясимфония.
lair
18.01.2017 09:42("Динамическое программирование" — оно про другое.)
Мемоизация — это способ борьбы с многократным вычислением одного и того же, а не с глубиной стека. А вот для борьбы с глубиной стека уже надо просто заменять алгоритм (либо на нерекурсивный, либо на алгоритм с хвостовой рекурсией).
mayorovp
18.01.2017 16:26-1Никакого "Принципиально другого алгоритма" придумывать не нужно. После того как вы сделали мемоизацию, достаточно просто перейти к рекурсивному алгоритму.
- Выбираем способ обхода (обычно оно очевидно)
- Пишем цикл, перебирающий параметры
- Пишем код, аналогичный вызову функции с этими параметрами, с учетом того что запомненного значения заведомо нет.
- Саму функцию меняем с учетом того что запомненное значение заведомо есть.
Вот ваш случай:
int a[100]; int f(int i) { if (i<2) return i; else { return a[i]; } } for (int i=2; i<100; i++) a[i] = f(i-1)+f(i-2);
Это что, теперь называется "придумывать принципиально другой алгоритм"?

bromzh
18.01.2017 07:29+2Вряд ли человек, который не знает, что такое рекурсия в программировании хоть что-то поймёт из этой статьи, тут какие-то обрывки мыслей вперемешку с копипастой из википедии, да и инфы-то тут никакой особо нет.
Ну а для того чтобы нормально понять, что такое рекурсия в программировании, какие её типы бывают, какие проблемы возникают и как с ними правильно бороться, вполне хватит прочитать главу 1.2. из небезызвестной SICP. Лучшего объяснения я не видел.
Можно было хотя бы разобрать алгоритмы и реализации программ, рисующих фракталы, чтобы было немного интересно. Но нет, тут только пара невзрачных картинок (даже Мандельброта и брокколи нет) без объяснений.
PS А пример на прологе мне не кажется таким уж наглядным, хаскель подошёл бы лучше, так как для подобных примеров (числа фибоначчи, факториал, функция аккермана, и т.п.) код практически совпадает с мат. определением этих ф-ций (ага, я тоже умею копипастить):
fac 0 = 1 fac n = n * fac (n-1) fib 0 = 1 fib 1 = 1 fib n = fib (n-1) + fib (n-2) ack 0 n = n + 1 ack m 0 = ack (m-1) 1 ack m n = ack (m-1) (ack m (n-1))
jknight
18.01.2017 09:47+2Если уж статья рассчитана на людей, которые не в курсе, что же такое рекурсия, зачем же давать им столь ядовитые примеры? Сугубо из математического представления? Факториал — еще ладно, хрен с ним(хотя бы не создает извратной сложности алгоритма, но так писать тоже нельзя), но вот вычисление чисел Фибоначчи должно выглядеть исключительно как пример, показывающий, к чему приводит рекурсия, если ее применять бездумно(с расчетом количества операций и объяснением, к чему это может привести), не как пример применения рекурсии. А я вот во всем тексте увидел только невнятное «большое дерево вызовов», которое этот новичок скорее всего пролистает…

apachik
18.01.2017 14:01+1Один мой одноклассник (олимпиадник-математик во время занятия информатикой) как-то сказал:
«Я долго не понимал что такое „динамика“, но когда мне объяснили, что динамика — это „рекурсия“, а рекурсия — это „индукция“, то все встало на свои места»
roman_kashitsyn
18.01.2017 14:25+2когда мне объяснили, что динамика — это „рекурсия“, а рекурсия — это „индукция“, то все встало на свои места
Непонятно, как всё могло встать на места, если оба утверждения являются неверными.
динамика — это „рекурсия“
Под динамическим программированием обычно понимают решение задачи через комбинацию решений перекрывающихся подзадач меньшего размера. Подзадачи должны образовывать ациклический направленный граф.
Когда же задача выражена в виде ациклический графа, его можно считать двумя способами: рекурсивно, используя мемоизацию для хранения решений перекрывающихся задач, либо не рекурсивно, если считать подзадачи в порядке, совпадающем с одной из топологических сортировок графа задач. Первый способ обычно проще, потому что так нужно меньше думать — машина сама неявно посчитает топологическую сортировку при обходе графа задач в глубину.
рекурсия — это „индукция“
Рекурсия движется от сложной структуры к простой, пока не дойдёт до тривиальной базы. Индукция движется от тривиальной базы к всё более сложным структурам. Поэтому рекурсия — это индукция, вывернутая наизнанку.

Deosis
19.01.2017 07:47В первом приближении динамика — это рекурсия наоборот.
В рекурсии сложную задачу разбивают на более простые пока не дойдут до тривиальных задач, а потом объединяют полученное решение.
В динамике сначала решают тривиальные задачи, потом объединяют и получают решения для все более и более сложных задач, пока не получат решение исходной задачи.

ParkeTg
18.01.2017 15:20Если вы не поняли, что такое рекурсия — прочитайте это предложение еще раз.

usrsse2
18.01.2017 17:26+1это цикл, а не рекурсия

syavadee
19.01.2017 02:19тогда рекурсия — это цикл в функциональной парадигме
mayorovp
19.01.2017 08:42Так, да не так. Во-первых, циклу эквивалентна только хвостовая рекурсия. Во-вторых, побудительное предложение является императивным — а потому к ФП отношения не имеет.
В-третьих, строго говоря, тут нет ни рекурсии, ни цикла — говорится же только прочитать предложение, а не делать что в нем написано :)

subirdcom
19.01.2017 18:52+1Самое известное программисту применение рекурсии — задачи на вычисление чисел Фибоначчи или факториала.
Вычисление чисел Фибоначчи — самая известная программисту задача, которую не надо решать ни за экспоненциальное, ни за линейное время.
nickolaym
27.01.2017 15:27+1А вторая такая задача — это вычисление определителя матрицы.
Формула в учебнике математики — через миноры — это яркий пример рекурсии, «как не надо делать».
Даже с мемоизацией. Тем более с мемоизацией.

lito_atreides
26.01.2017 00:18-1Когда диссер писал, то где-то вот здесь находил материал по теме http://mmse.xyz/

nickolaym
27.01.2017 15:21+1«Любую рекурсию можно переписать без использования рекурсии»?!
Стек данных вместо стека возвратов — нет ли здесь размена шила на мыло и подмены понятий?mayorovp
27.01.2017 15:37Суть в том, что у нас всего 1 мегабайт стека возвратов — и все адресное пространство для стека данных! :)

nickolaym
27.01.2017 16:06Размер стека возвратов регулируется, во-первых, и легко обходится, во-вторых.
При достижении определённой глубины просто берём и вызываем функцию в контексте другого потока (можно даже другого процесса) (можно даже на другой машине в вычислительном кластере).
Стек возвратов — универсальный инструмент, и в силу универсальности, избыточный.
Если для вычисления рекурсивной функции у нас есть, грубо говоря, две-три-четыре точки возврата, то для кодирования их нам достаточно одного-полутора-двух бит, причём зачастую, эти значения можно даже не хранить, а вычислять из текущего контекста.
Поэтому в конкретной функции стек данных решает. То есть, мы пишем свою маленькую виртуальную машинку под конкретную задачку.


AnutaU
У вас в примере не хвостовая рекурсия: после рекурсивных вызовов выполняется сложение.
plaguedo
Спасибо вам за замечание, исправил.