
Всякий, знакомый с проблематикой кодирования информации, периодически сталкивался с идеями алгоритмов «суперсжатия» данных без потерь. Зачастую предлагается использование хеш-сумм, генераторов случайных чисел (зачем?), или просто различных комбинаций повторного сжатия данных при помощи архиваторов. После очередного бурного обсуждения, как правило, эксперты в очередной раз советуют первооткрывателям ознакомиться с азами теории информации. Особо упертым предлагают просто написать программу сжатия данных на один бит файла со случайными данными. После этого доселе бурно проходящее обсуждение «революционной технологии» постепенно сходит на нет.

Проблематика завлекает
Много лет назад, в ходе работы над программой анализа текстов, я также заинтересовался этой темой. В результате изучения фундаментальных основ современной теории информации, стало понятно, об какие камни спотыкались многочисленные первопроходцы, пытавшиеся с наскока решить эту проблему.
Первоосновы…

Все дело в структуре данных
Сжатие данных базируется на энтропийной кодировании, основанном на усреднении частот появления элементов в закодированной последовательности. То есть, только если символы некоторой последовательности данных встречаются в ней с различной вероятностью, тогда можно осуществить сокращение данных без потери информации. При этом, после такого сжатия в получившейся последовательности, частoты, с которыми появляются отдельные знаки, практически одинаковы (энтропия достигает своего максимального значения).

В глазах у Шеннона вселенская грусть — у сжатия данных есть свой предел
Согласно обратной теореме Шеннона об источнике кодирования, максимальная степень сжатия с помощью кодирования без потерь ограничивается энтропией источника. То есть, простыми словами — нельзя сжать данные больше, чем позволяет их энтропия, которая в свою очередь вычисляется по формуле:
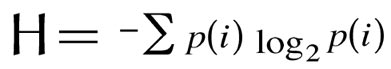
Из вышесказанного следует, что если логарифм вероятности появления того или иного элемента в данных, равен длине этого элемента, получить выигрыш от кодирования не удастся. При этом, после сколько-нибудь существенного сжатия данных без потерь, частoты распределений символов в получившейся последовательности стремятся к равномерному распределению, а стало быть, степень повторного сжатия этих данных стремится к нулю.
Не обязательно быть знакомым с основами теории информации, чтобы проверить верность этого утверждения. Достаточно взять любую программу для сжатия данных будь-то zip или rar, и попробовать повторно сжать уже заархивированный файл. Либо степень сжатия такого файла будет ничтожно мала, либо, что более всего вероятнее, повторное сжатие файла приведет к его увеличению (поскольку программа сжатия добавит к уже имеющемуся объему данных некоторую служебную информацию). То же самое произойдет и с другими программами для сжатия данных без потерь информации, даже с самыми эффективными.
Информационный взрыв
Как видим, существующие технологии кодирования информации бессильны перед существующим фундаментальным теоретическим пределом сжатия данных. При этом необходимо учитывать, что по одной оценке только в 2008 году было создано 487 миллиардов гигабайт цифровых данных. В 2011 году сгенерировано 1,8 трлн. гигабайт данных. А в 2012 создано уже в 5 раз больше цифровой информации, чем в 2008 году. При этом надо понимать, что речь в данном случае идет только о сохраненных данных — вся остальная информация, судя по всему, была для нас бесследно утеряна из-за банальной нехватки места для ее хранения. К настоящему моменту на планете Земля насчитывается более триллиона мобильных устройств. Только за один день создается более 2,5 млрд. гигабайт данных. То есть 500 млн. компакт-дисков данных ежедневно, которые можно выставить туда и обратно в два ряда от Солнца до планеты Плутон (пользователи написали, что возможно расчеты неверны — авт.).
В итоге, для хранения всей этой информации информационные компании постоянно увеличивают количество дата-центров. И этим гигантским сооружениям постепенно уже становится мало места на суше — данные переправляются в мировой океан, на плавучие дата-центры. И, увы, вся эта колоссальная масса электроники непрерывно потребляет огромное количество энергии и выделяет соответствующее ей количество тепла в атмосферу Земли.

Один из дата-центров. Матрица отдыхает...
Пытаемся обуздать хаос

Некоторые хаос почему-то представляют так...
Однако, при всей насущной потребности прорыва в технологиях сжатия данных, мы заходим в тупик фундаментальных основ теории информации. Поэтому, прекратив попытки пробить головой стену энтропийного предела сжатия данных, я решил более пристально изучить из чего, собственно, состоит эта стена. А состоит она из данных, энтропия которых стремится к максимальной, то есть, попросту говоря из хаоса.

Хотя он выглядит примерно так...
Именно хаос мы увидим, рассматривая данные сжатого файла. Возможно, это и не самый идеальный источник случайных данных, но в плоскости практического применения в сфере сжатия данных вполне подходит. Ведь достаточно найти хотя бы одну закономерность в этом хаосе, и ее будет можно использовать для дальнейшего сжатия данных.
Находим бреши в коде Вселенной

Казалось бы, нет более противоположных понятий, чем закономерность и хаос. Но, как оказалось, закономерности в хаосе тем не менее есть… На солнце есть пятна, а в хаосе есть свои закономерности.
Как уже было сказано ранее, если логарифм вероятности появления какого-либо элемента в данных не соответствует его длине, это дает возможность, согласно теореме о кодировании, сжать такие данные. Но существуют ли такие элементы в данных, энтропия которых максимальна?

Внимательно посмотри и найди 10 закономерностей (шутка)
Да, такие элементы имеют место быть в любых данных, энтропия которых близка к максимальной настолько, что их дальнейшее сжатие невозможно (в рамках существующих теоретических основ). В своих исследованиях я продвигался от более сложных структур данных к наиболее простым, так сказать, неким первоосновам или «атомам» хаоса.
Интересно? Следуй за
Что внутри кроличьей норы
Рассмотрим бинарный (двоичный) код сжатых данных, которые не поддаются дальнейшему сжатию никакой из существующих программ сжатия данных.
Возьмем, и последовательно слева направо заменяем все сочетания из трех знаков, из которых два знака одного вида находятся по бокам, а один знак другого вида находится посредине (проще говоря, сочетание «010» или «101») — активное кодовое слово (АКС) на новый знак, например, знак «2».
Например, во фрагменте «111000110101000010111» мы найдем два сочетания «101»: «1110001<101>010000<101>11» (знаки "<" и ">" приведены только для выделения АКС). После замены их на «2», фрагмент выглядит так: «11100012010000211». В результате такой замены, например, в 20 миллионах бит кода будет примерно 2001550 всех знаков «2».
Казалось бы, это означает, что данное сочетание появляется в коде с вероятностью 2001550:20000000=0.1000775, что дает ее двоичный логарифм в 3.320810439 бит. Однако это совсем не так. Тут не все так просто…
Допустим, мы убрали из кода все эти знаки «2». После этого мы опять обнаружим в нем эти же АКС “101”. Откуда они там взялись? А взялись они из сочетаний наподобие “110101,” которые мы заменили сначала на “1201”, а убрав “2” получили опять то же АКС “101”.
Например, после изъятия их из вышесказанного фрагмента, он выглядит так: «111000<101>000011». Сочетание «101» появилось после изъятия двойки из отрезка фрагмента «1201». Стало быть, в полученном фрагменте для восстановления первоначального состояния нужна информация только о расположении одного знака “2”, т. к. очевидно, что другая двойка обязательно должна будет расположена после первого знака в сочетании «101» — «1201» («1110001201000011»). Все двойки, которые располагались в подобных местах, можно не указывать в данных о расположении двоек. Значит для восстановления первоначальных данных, нам необходимы сведения только о расположении не 2001550, а 2001550-234200=1767350 двоек (где 234200 – это количество вновь появившихся АКС после того как мы убрали все 2001550 двоек из 20 000 000 бит кода с энтропией близкой к максимальной (ЭБМ)).
Кроме этого, необходимо учитывать, что двойка никогда не может располагаться после сочетания «10» (вот так — «102»), поскольку в результате предыдущих замен “101” на “2” отрезок «10101» превратился бы в «201», а не в «102» (т. к. замена идет слева направо), а затем (уже после изъятия двоек) останется «01». Поэтому все места после сочетаний «10» (после замены АКС на двойки) определяют как запретную зону (ЗЗ) для вставки новых двоек. Например, во фрагменте до изъятия двоек «11100012010000211» обнаружилось две таких ЗЗ — «1110*0012010*000211» (отмечены звездочками), что уменьшает число вариантов расположения АКС (двоек) — среди фрагмента«111H01201H00211» (где знаком «H» заменили «00»).
С учетом вышеизложенного, код расположения (КР) двоек для этого фрагмента можно записать в виде строки «00000000000200», и уже теперь убирать все двойки из фрагмента, который можно записать в виде строки “111H0101H0011”. Заменив знак H опять на «00», получаем «111000101000011».
Если проделать все эти замены в бинарном коде с ЭБМ, то вероятность появления двойки в КР получаем примерно 0.128-0.1285, что дает нам отрицательный двоичный логарифм в пределах 2.965-2.96, что, как мы видим, меньше битовой длины АКС. При этом уникальность ситуации заключается в том, что эта закономерность соблюдается вне зависимости от того, какого типа, структуры, вида файл был сжат. Главное, чтобы получившиеся в результате сжатия данные, имели ЭБМ, или проще говоря, их нельзя было сжать повторно.
Код хаоса взломан — что дальше?

Что делают хакеры, взломав код банка? Похищают деньги! Мы тоже будем похищать, но не деньги, а энтропию, внося во вселенский хаос упорядоченность и спасая вселенную от ее энтропийной (или тепловой) смерти.
Для 20 000 000 бит данных с ЭБМ в результате вышеуказанных манипуляций, мы получим не сжатый КР длиной примерно 13757030 бит (1767350 двоек среди 11989680 остальных знаков, которые мы обозначаем нулями). Код по формуле вычисления энтропии можно сжать до 7610719.618 бит. Логарифм (по основанию 2) отношения количества двоек к количеству всех знаков в этом примере равен 2.960509361 бит.
Что теперь делать? Записываем полученный КР 7610719.618 бит на
Давайте посмотрим: нам нужно взять КР 1712811 знаков среди остальных 11989680 знаков (такой КР сжимается по формуле энтропии до 7448185.838 бит), что и даст нам требующуюся вероятность 0.125. Найти такой код проще простого — подобрать по нужному количеству один из знаков в восьмеричных данных с ЭБМ (3-битный восьмеричный алфавит), и перенести его КР в виде нового расположения двоек, которое будет соответствовать расположению изъятого знака из 8-ричных данных.
Каков выигрыш в сжатии данных от этих действий? Заменив одно количество АКС на другое, мы уменьшили общую длину сжимаемых данных на 54539 АКС (каждое длиной в три бита), т. е. уменьшили объем данных на 163617 бит. При этом, благодаря изъятию двоек среди остальных знаков, первоначальный код расположения 7610719.618 бит необходимо было сохранить для дальнейшего его восстановления. Зато вместо него размещением АКС в новом расположении, среди оставшихся, после удаления первоначального количества АКС, знаков, был записан другой код расположения АКС имеющий объем 7448185.838 бит (на который был уменьшен объем данных в восьмеричных данных с ЭБМ, которые мы превратили в 7-ричные, получив тот самый выигрыш примерно в 7448185 бит), что дало в разности увеличение кода на 7610719.618-7448185.838=162533.7798 бит. Однако общее уменьшение данных составило 162533.7798-163617=-1083.220189, т. е., округляя, 1083 бит.
«Бесконечное сжатие» для бесконечных данных

Конечно, можно возразить, что столь малая степень сжатия (20 миллионов бит мы сокращаем только на 1083 бит) является весьма небольшой. Однако нужно отметить, что в случае применения данного кодирования данных для их сжатия, такое сжатие можно повторить вновь и вновь.
В связи с этим необходимо разъяснить суть выражения «бесконечное сжатие». Естественно, что сжатие некоторых конечных данных возможно до определенного предела, который обусловлен конкретным видом кодирования, подобному вышеописанному. То есть, мы можем уплотнить какое угодно количество данных до определенного минимума (например, в вышеуказанном примере осуществления «бесконечного сжатия», возможно, например, уплотнить 20 гигабайт данных с ЭБМ до, например, 20 мегабайт, но, пока, отнюдь не до 200 байт). При этом, в дальнейшем, такой полученный несжимаемый минимум данных можно будет соединить с другими полученными минимумами данных и опять сжать уже объединенные таким образом данные вышеуказанным способом. Поэтому, именно для неограниченного объема данных существует возможность неограниченного уплотнения. Ограниченный объем данных уплотняется до некоторого определенного минимального предела.
«Прочитал, допустим, это правда. В чем подвох?»
Да, действительно, подвох, или скорее нюанс, действительно имеется. Суть этого нюанса заключается в том, что на этапе сжатия данных КР АКС в арифметическом кодировании необходимо применять более длинную арифметику, чем имеется в известных мне программах сжатия данных. Обычно при арифметическом кодировании более длинная арифметика не дает ничего в практическом плане, давая выигрыш в сжатии в ничтожно малые доли процентов, весьма существенно замедляя при этом время сжатия. Однако, в данном случае, эти ничтожно малые доли процентов являются критичными в ходе каждого цикла сжатия.

Пока Гарольд под прикрытием сеет доброе вечное, молодой гений пишет на листочке код программы суперсжатия… (Person of Interest S02E11 (С)
Так что, обращаюсь ко всем толковым программистам с предложением написать модуль арифметического кодирования с более длинной арифметикой на более быстром языке программирования, нежели BASIC. Чуть позже выложу файл с КР АКС, чтобы предметно было видно, с чем придется иметь дело при сжатии.

Стартап это еще тот адреналин. Ведь на самом деле всё только начинается...(Silicon Valley (С)
Все авторские права и прочая интеллектуальная собственность принадлежат их законным правообладателям (в том числе мне ;). Все изображения приведены только в качестве учебных иллюстраций и принадлежат их законным правообладателям. Patents pending.
==========
В связи с критическими замечаниями, которые возникли в ходе обсуждения данной статьи, добавляю краткий FAQ:
Вопрос. Как можно всерьез обсуждать сжатие случайных данных? Вот доказательство невозможности этого: www.compression.ru/arctest/descript/comp-hist.htm «Таким образом, этот мысленный эксперимент доказывает, что программы, которая сжимала бы каждый файл… не существует».
Ответ. В данном доказательстве речь идет о «взаимооднозначном сопоставлении», которое имеет место быть в статистическом и комбинаторном сжатии. В данном случае рассматривается третий подход к сжатию данных — алгоритмический. Его общее описание и строгий математический анализ здесь: compression.ru/download/articles/ti/kolmogorov_1965_three_way_pdf.rar (А.Н.Колмогоров. Три подхода к определению понятия «Количество информации» см. §3 Алгоритмический подход)
Возьмите, например, 3 миллиона двоичных знаков числа ? и попробуйте сжать любой существующей программой сжатия. Получить результат меньше трех миллионов бит (или 375000 байт) у Вас не получится. Гораздо короче просто сохранить программу, которая воспроизводит путем вычисления эти три миллиона (или хоть 3 миллиарда) двоичных знаков.
В. Но алгоритмов (программ) меньшей длины опять-таки меньше, чем вариантов исходных данных.
О. Нет, Колмогоров в вышеуказанной статье математически доказал обратное в рамках инструментария теории алгоритмов. Другими словами для любых данных, некоторой достаточно большой длины, всегда найдется программа точно воспроизводящая эти данные, запись которой будет меньше, чем длинна этих данных.
При этом Колмогоров вводит понятие «колмогоровская сложность» — сложность создания алгоритма, который воспроизводит конкретные данные.
В. Значит, нужны колоссальные вычислительные мощности?
O. Не нужны. Справляюсь на обычном компьютере :)
В. У меня есть два байта — сможете сжать до одного бита?
O. Технические ограничения данного алгоритма позволяют сжимать блок случайных данных с размером не менее 100 килобайт.
В. Означает ли это что можно сжимать любое количество данных до этого минимального размера?
О. Теоретически да. За один проход данные сжимаются с коэффициентом около 0.99995. Поэтому необходимо учитывать, что чем больше данных, тем больше это займет времени.
В. Честно признаю, текст не осилил. Если кто-то дочитал, можете, пожалуйста, вкратце пересказать идею автора?
О. Статья в кратком изложении:
Автор проводил исследования хаотически расположенных данных, у которых мера хаоса (энтропия) максимальна. В этом хаосе автор нашел некоторые структуры данных, которые более упорядочены (менее хаотичны) чем другие. Вместо того чтобы писать статьи в научные журналы и получать
В. Ваш алгоритм я не проверял, но он все равно не работает.
О. Человеку, знакомому с азами программирования, элементарно в течение часа удостовериться в результатах расчетов, приведенных в статье.
В. Зачем мне тратить свое драгоценное время на это, если я могу его потратить на написание разгромных (хоть и бездоказательных) комментариев? Зачем автор заранее раскрыл содержание алгоритма, пытаясь ввергнуть ни в чём не повинных людей в болезненный процесс мышления, вместо того, чтобы его засекретить и просто продавать программу дата-центрам?
О. По первому вопросу: Мозги без использования застаиваются :) По второму вопросу: автор погрузился в размышления… ;)
==========
Краткий FAQ к тестовой программе AIunCoder01.exe
Вопрос. Где скачать?
Ответ. www.ILIN.biz/files/AIunCoder01.zip
В. Что это?
О. zip-архив с папкой AIunCoder01 в которой находятся файлы AIunCoder01.exe, ai1-locat.txt, ai2-field.txt
В. Что это за файлы?
О. Это бинарные (двоичные) файлы, на которые мы разложили тестовый файл AMillionRandomDigits.bin. В частности ai1-locat.txt — это файл кода расположения АКС (101), а файл ai2-field.txt — это файл кода который остался после изъятия этих АКС. AIunCoder01.exe – это декодер, который восстанавливает из этих кодов исходный файл AMillionRandomDigits.bin.
В. Что мне с ними делать?
О. Скопировать все 3 файла на диск С:\ (в корневую директорию) и запустить декодер AIunCoder01.exe (на часик или больше в зависимости от мощности компьютера ;) после чего на диске С:\ раскодируется AMillionRandomDigits.bin
В. Что это за файл AMillionRandomDigits.bin?
О. «Широко известный в узких кругах» файл AMillionRandomDigits.bin выложен Марком Нельсоном на своей страничке (marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin) в 2002 году как пример нагромождения случайных данных, которые невозможно сжать существующими способами сжатия данных. И действительно с 2002 года его еще до сих пор никто не сжал. Подробно обо всех попытках получить денежный приз можно почитать на страничке Нельсона: marknelson.us/2006/06/20/million-digit-challenge/
В. А вы что его сжали?
О. Пока нет, но близок к этому. Выложенные мной файлы демонстрируют работоспособность алгоритма разложения исходных файлов на части, которые можно затем сжать и самое главное возможность, затем из этих частей восстановить первоначальный файл.
В. Еще чем-то примечательны выложенные вами файлы?
О. Примечательно то, что в файле кода расположения ai1-locat.txt количество указаний на АКС (количество единичек, которые находятся среди остальных знаков, представленных нулями) значительно меньше, чем самих изъятых АКС. И сама длина кода расположения существенно короче первоначальной длины двоичного представления исходного файла AMillionRandomDigits.bin.
В. И о чем нам это должно говорить?
О. А о том, что благодаря найденным закономерностям в случайных данных, в которых по самому определению эти закономерности должны отсутствовать мы можем несколько сократить код представления этих данных, частности больше чем позволяет их энтропия, перепрыгнув через «энтропийный барьер».
В. Почему же тогда в таком случае вы не сжали сам файл AMillionRandomDigits.bin?
О. Для этого необходимо произвести арифметическое кодирование файла кода расположения ai1-locat.txt как можно с меньшими потерями как можно ближе приблизившись к теоретическому пределу сжатия.
В. Каков этот предел и насколько это возможно?
О. Этот предел обозначен формулой вычисления энтропии и для данного файла составляет до 1261269 бит. Это возможно, использовав длинную арифметику для арифметического кодирования этого файла. По сути ничего сложного.
В. И что нам это даст?
О. Еще раз подробно напишу алгоритм действий:
Мы взяли этот тестовый файл AMillionRandomDigits.bin длиною 415241 байт. Длина его бинарного файла (то есть двоичного) 3321928 бит.
Длина кода расположения АКС для него (ai1-locat.txt) 2286631 бит (292405 единиц и 1994226 нулей). Логарифм вероятности появления АКС — 2.96718368674378 при длине самого АКС три бита. Итого такой код сжимается по формуле Шеннона до 1261268.904 бит.
Затем мы АКС убираем, и записываем в оставшиеся после этого данные длиною 1994226 бит (ai2-field.txt) те же АКС в новом расположении и в новом количестве, с таким кодом, у которого логарифм вероятности появления АКС — равен длине АКС 3 бита. Для того чтобы так получилось это должно быть 284890 АКС среди 1994226 остальных знаков ai2-field.txt, такой новый код расположения имеет энтропию по формуле Шеннона 1238846.109 бит. (Причем этот код мы берем не произвольно, а из определенной части сжимаемых данных (например, код расположения одного из знаков восьмеричного кода имеет примерно такую же вероятность)).
При этом необходимо заметить, что не обязательно вероятность появления АКС в новом коде расположения должна быть _точно_ равна вышеуказанному параметру (0.125). Просто максимум функции сжатия достигается именно при равенстве логарифма вероятности появления АКС его длине.
Итого мы сокращаем -7515 АКС по 3 бита = -22545 бит.
Код расположения уменьшился на 1238846.109 — 1261268.904 = -22422.79479.
Разница составляет -22545 — (-22422.79479) = -123.9194967 бит суммарного уменьшения кода всех данных.
В. Ну и что это нам дает?
О. Сжатие данные на величину, превышающую их энтропию, позволяет производить их многократное повторное сжатие, преодолевая энтропийный предел сжатия данных. Простыми словами сжимать колоссальные массивы информации до определенного минимума.
В. И каков этот минимум?
О. По предварительным расчетам в пределах конкретного алгоритма данного способа сжатия до одного мегабайта.
В. В чем подвох?
О. Теоретические возможности, которые открываются при применении данного способа сжатия данных настолько выходят за рамки устоявшихся уже почти за сто лет привычных представлений, что даже серьезные специалисты вместо проверки самого (довольно несложного) алгоритма кодирования, предпочитают доказывать его теоретическую несостоятельность, несмотря на очевидные практические результаты.
• А.Н.Колмогоров. Три подхода к определению понятия «Количество информации» см. §3 Алгоритмический подход (http://compression.ru/download/articles/ti/kolmogorov_1965_three_way_pdf.rar)
• Малинецкий Г. Г. Хаос. Структуры. Вычислительный эксперимент. Введение в нелинейную динамику. 3-е изд. М.: УРСС, 2001.
Комментарии (264)

ploop
03.04.2015 10:33+5Опять вечный двигатель. Математический :)
Тема очень интересная, тоже увлекался подобным.
ILIN-AIC Автор
03.04.2015 12:11Ну не совсем вечный двигатель, а скорее «эликсир бессмертия». То есть нечто такое, что теоретически достижимо… Просто пока никто не знал как. Ниже привел цитату из статьи Колмогорова, где он рассуждает о теоретической возможности такого «эликсира», при алгоритмическом подходе.
Кстати ссылка: compression.ru/download/articles/ti/kolmogorov_1965_three_way_pdf.rar (Три подхода к определению понятия «Количество информации»)

icoz
03.04.2015 14:03+1Да, я думаю, что многие на определённом этапе своего ит-развития проходили через изучение/изобретение алгоритмов сжатия. Потом, побнабравшись знаний и опыта, бросали это дело. Крайне сложно в одиночку решить данную проблему лучше целых отделов учёных в различных институтах.

ploop
03.04.2015 16:31+1На самом деле я считаю это очень хорошим делом. Как дети изобретают физические вечные двигатели в виде колёс с грузиками и т.д. лет в 10, так и айтишники на первых этапах познания пытаются изобрести подобные велосипеды. Это значит, что есть стремление, мозг работает, изобретает, есть азарт!
То есть догмы «дядя сказал, что нельзя, значит нельзя» надо откидывать. Пусть банально и смешно это выглядит первое время, но эта жилка принесёт плоды в будущем, если не угаснет.
mekegi
06.04.2015 15:49+3Ох уж эти «горящие глаза» и «целые отделы ученых»
Основы математики, биекция, мощность множества и элементарный здравый смысл должны подсказать что в «сжатии данных» граалей нет и быть не может.
Но судя по таким статьям и комментам тут ситуация крайне плачевная.
ploop
06.04.2015 16:09Основы математики, биекция, мощность множества и элементарный здравый смысл должны подсказать что в «сжатии данных» граалей нет и быть не может.
Это известно изначально. Но попытки что-то придумать в этом направлении, просто в целях обучения, очень подтягивают опыт в смежных областях. Например, попытка написания макетной программы сразу вызовет необходимость окунуться в битовую логику, познать некоторые нюансы своего языка программирования, приёмы оптимизации, и т.д.

kahi4
03.04.2015 10:37+10То есть 500 млн. компакт-дисков данных ежедневно, которые можно выставить туда и обратно в два ряда от Солнца до планеты Плутон.
Перигей орбиты Плутона — 4,437 млрд км. У вас один компакт-диск размером в 16 км?
А по делу: знаете, я вот очень люблю проверку своих идей следующим вопросом: а сделал ли кто-то уже так же? и если нет, то почему? В подавляющем количестве случаев это не сделал никто, потому что это либо имеет глубокие подводные камни, которые всплаывают при реализации и все ломают, либо это попросту не нужно.
По алгоритму: допустим, имеем последовательность 10101, меняем на 201. Хорошо. Как восстановить обратно, если у вас 2-ка означает и 101, и 010? Более того, где-то я уже это видел (zip), только более строгом формате, где ваша «2» — ключ из словаря.
kahi4
03.04.2015 10:41+1Ну и чуть своих идей: пока все вдохновляются космосом и макромиром, я вдохновляюсь крошечными белковыми соединениями — ДНК (и РНК). Чует сердце мое, что можно как минимум скрипты эффективно сжимать подобным образом. А если взять скрещивания и мутации… кто же не мечтал, чтобы его программа могла само-воспроизводиться, внося случайные изменения в свой код? Идеальный адаптирующийся вирус, который самостоятельно будет находить 0-Day уязвимости. Но это уже совсем мечты*, а вот принципиально иное сжатие как минимум для скриптов вполне реально. И что-то мне подсказывает, что я тут не первый, просто ничего по теме не попадалось.
* потому что чтобы работал генетический алгоритм, ему нужно указать функцию эффективности. Выживать должны те популяции, которые наиболее эффективны. А это самое сложное.

ILIN-AIC Автор
03.04.2015 11:20Про Плутон — увы «мопед не мой»… Вы меня слегка успокоили :)
А по алгоритму: у нас 2-ка означает или 101, или 010.
Просто тут принцип симметрии…
EugeneButrik
03.04.2015 14:04+5Простите, а в каком виде Вы собираетесь хранить её (двойку) в бинарном файле архива?
P.S. Пожалуй оставлю это тут )
ploop
03.04.2015 16:33+2в каком виде Вы собираетесь хранить её (двойку) в бинарном файле архива?
Про это обычно задумываются, когда дело до реализации доходит. Как и адрес повторяющейся последовательности, который по размеру превосходит саму последовательность, и другие нюансы, которые разбивают мечты в прах :)

Alexnn
03.04.2015 10:51+4«Поэтому, именно для неограниченного объема данных существует возможность неограниченного уплотнения. Ограниченный объем данных уплотняется до некоторого определенного минимального предела.»
это можно перевести в «бесконечность можно уменьшать бесконечность раз. от этого она меньше не станет. А вот ограниченный объём уплоняется по Шеннону. А те кому это не нравится могут идти за Бабушкиным»?
www.compression.ru/arctest/descript/comp-hist.htm
«Вы начали с предположения о том, что в вашем распоряжении есть совершенный метод сжатия, который должен сжимать каждый из файлов. В результате эксперимента стало очевидно, что по крайней мере два файла, различавшихся до сжатия, стали совершенно одинаковыми после сжатия. Однако методов, позволяющих из двух идентичных файлов в результате декомпрессии получить два разных оригинала, не существует!
Таким образом, этот мысленный эксперимент доказывает, что программы, которая сжимала бы каждый файл и могла бы затем при необходимости все корректно распаковать, не существует. Конечно, программа сжатия, не позволяющая вам восстанавливать исходные данные, практически бесполезна. (Чтобы уменьшить размер газеты, вы можете ее сжечь, однако после этого узнать, что в ней было написано, будет довольно сложно.)…
»
kahi4
03.04.2015 11:03-6Почему же не существует? Вероятностные методы. Только вот получить обратно нужный файл крайне маловероятно.
Или вот еще одна идея, потенциально сжимающая данные в n раз: заменяем последовательности 01, 10 на 0, а 00 и 11 на 1. В итоге имеем сжатие в два раза независимо от энтропии. Берем хеш от исходного файла. Восстанавливаем перебором, пока не получим файл, хеш которого совпадает с исходным. Что ж, мы сжали практически в два раза любой файл (чей размер значительно превосходит размер хеш-суммы), только разжимать его будет несколько долго, да еще можно напереть на коллизию, но это меньшая из проблем (взял две разные хеш-функции. Коллизия одновременно для двух, помнится мне, в порядке погрешности).
Мало сжимать в два раза? даешь больше0000 0001
0010 0011
0100 0101
0110 0111
заменяем на 0
1000 1001
1010 1011
1100 1101
1110 1111
Заменяем на 1
Сжатие в 4 раза не зависимо от энтропии.
ILIN-AIC Автор
03.04.2015 11:55+2«В итоге имеем сжатие в два раза независимо от энтропии. Берем хеш от исходного файла. „
Это то о чем я написал в начале статьи. Тут все дело именно в коллизиях, чтобы их не было хэш должен быть такого размера, что выигрыш в сжатии будет полностью нивелирован.
kahi4
03.04.2015 15:24Да, что-то я замечтался и не подумал.
Подумал только об огромном количестве времени, необходимом на восстановление данных (покуда нужно перебрать все возможные варианты).

ILIN-AIC Автор
03.04.2015 11:43-2Ну про Бабушкина — мне кажется тут комментировать нечего…
Про мысленный эксперимент это уже интересней. Много лет назад ознакомился с данным доказательством от противного. Но, к сожалению, в данном случае оно не в тему, поскольку там речь идет о простой табличной подстановке. Здесь же речь идет об изменении данных алгоритмическим путем.
Привожу свою очередь другую цитату с того же сайта:
А.П.Колмогоров
Три подхода к определению понятия «Количество информации»
§3 Алгоритмический подход
«Конечный результат построения инвариантен по отношению к переходу к новой нумерации n'(x), обладающей теми же свойствами и выражающейся общерекурсивно через старую, и по отношению к включению системы X в более обширную систему X' (в предположении, что номера n' в расширенной системе для элементов первоначальной системы общерекурсивно выражаются через первоначальные номера n). При всех этих преобразованиях новые «сложности» и количества информации остаются эквивалентными первоначальным в смысле ?
«Относительной сложностью» объекта y при заданном x будем считать минимальную длину l(p) программы p получения y из x. Сформулированное так определение зависит от «метода программирования. Метод программирования есть не что иное, как функция ?(p,x)=y, ставящая в соответсвие программе p и объекту x объект y.
В соответсвии с универсально признанными в современной математической логике взглядами следует считать функцию ? частично рекурсивной.
[…]
За пределами этой заметки остается и применение построений §3 к новому обоснованию теории вероятностей. Грубо говоря, здесь дело идет о следующем. Если конечное множество M из очень большого числа элементов N допускает определение при помощи программы длины, пренебрежимо малой по сравнению с log2N, то почти все элементы M имеют сложность K(x), близкую к log2N. »

StrangerInRed
03.04.2015 11:07+3Осталось решить проблему с кодировокой вствляемой двойки, и все profit. Конечно же не, боже мой. Не будет никакого бесконечного сжатия. Сжимать можно чуть лучше, если пойти через теорию хаоса и аттрактор (https://ru.wikipedia.org/wiki/%D0%90%D1%82%D1%82%D1%80%D0%B0%D0%BA%D1%82%D0%BE%D1%80) но не бесконечно.

ILIN-AIC Автор
03.04.2015 11:47Ну, проблемы как таковой, мне кажется тут нет…
А насчет теории хаоса — это уже ближе к теме

tolika
03.04.2015 11:16В принципе, мышление как раз и является потугами сжать имеющуюся информацию (а заодно получить/предсказать по каким-либо причинам недоступную)…
Шеннон — это, конечно, хорошо, НО наверняка практически в любом представлении естественной информации (природной или «сотворенной» человеком) имеются какие-то скрытые зависимости (возможно не совсем очевидные и не обязательно связанные с частотностью встречаемости элементов представления или их последовательностей).
Например, в последовательности 123456789987654321 формально сплошная энтропия, а ежели присмотреться, то порядок.
Это я к тому, что идеальная программа сжатия должна искать скрытые зависимости, т.е. идти не по пути запоминания (на уровне мнемонических уловок), а анализа и «понимания» информации.
Естественно, в силу ограниченности ресурсов придется пойти на некие компромиссы, но это уже чисто технический вопрос… Так, например, в компьютере все вычисления тоже приближенно производятся, но благодаря точным методам вычислительной математики удается достичь достаточной точности.
ILIN-AIC Автор
03.04.2015 12:03Рад, что Вы, в целом, уловили мою мысль. Однако насчет вашего замечания:
«Это я к тому, что идеальная программа сжатия должна искать скрытые зависимости, т.е. идти не по пути запоминания (на уровне мнемонических уловок), а анализа и «понимания» информации.»
Могу сказать что то что вы описали — это ничто иное как искусственный интеллект колоссальной вычислительной мощности.
«Естественно, в силу ограниченности ресурсов придется пойти на некие компромиссы, но это уже чисто технический вопрос… „
То то и оно, что все упирается в ресурсы, которых пока у человечества нет. Поэтому я и использую вышеприведенную дыру в коде хаоса.

JuraZ
03.04.2015 14:02-2Возможно толика имел ввиду что под конкретный тип данных подбирается соответствующий лучший алгоритм зжатия. Например, для картинок один алгоритм, для видео другой, для текста третий. И даже дальше — для картинок типа А испoльзуем алгоритм типа А, и так далее. Что вообще-то на сегодняшний день мы и имеем.
А автор же хочет создать универсальный алгоритм, не так ли?

dtestyk
03.04.2015 14:19программа сжатия должна искать скрытые зависимости
может это поможет: Distilling Free-Form Natural Laws from Experimental Data

Gorthauer87
03.04.2015 12:11+1Вот поэтому мозг сжимает информацию с потерями и может запоминать намного больше информации.

ILIN-AIC Автор
03.04.2015 12:17Интересная теория… Правда то, что иногда выдают люди под гипнозом, ее несколько ставит под сомнение…

Gorthauer87
03.04.2015 13:43Там всё равно детали незначительные теряются. Точнее выдумываются заново.

JuraZ
03.04.2015 14:08Предлагаю просмотр курса «Lear How to Learn» нa Coursera — www.coursera.org/learn/learning-how-to-learn/outline

MiXaiL27
06.04.2015 04:54Эта теория очень легко опровергается. Когда посмотрели ЭЭГ загипнотизированного человека, то увидели активную работу лобный долей и других участков мозга, отвечающих за мышление и воображение, так что с потерями.

ILIN-AIC Автор
03.04.2015 12:28Тут мне пришел на почту вопрос: серьезно ли я насчет записи данных на бумажке? А как же… Нанотехнологии же! Шутка конечно :) просто в ходе редактирования статьи забыл зачеркнуть. Насколько я понял, я пока не могу отредактировать свою статью. Кстати на хабре есть хранилище, куда можно будет залить программу?

emreu
03.04.2015 12:30+1Когда-то тоже интересовался алгоритмами сжатия, пытаясь придумать свой супер-крутой метод. Дойдя до понимания того, что все существующие алгоритмы упираются в предел энтропии, нашёл такую лазейку — если обрабатывать данные большими блоками но на уровне отдельных бит, вероятность встретить «1» будет примерно 50%. Таким образом у блока длинной N будет N/2+delta бит «1» и N/2-delta бит «0», где delta не очень большое число (собирал статистику на разных больших файлах). Зафиксировав delta мы имеем всего C(N, N/2+delta) возможных перестановок «1», множество которых можно разбить на меньшие множества с числом элементов равным C(N, 1), C(N, 2),… C(N, k) (где k не превышает N/4 кажется, сейчас точно не помню) и установить отображение с блока, имеющего N/2+delta бит «1», на блок со значительно меньшим числом бит «1». Если правильно подобрать такое отображение, то можно нехило уменьшить число «1» в блоке и энтропию, после чего попробовать сжать блок ещё раз. Из накладных расходов — только сохранение числа delta, которое влезает в 2 байта для многокилобайтных блоков. Застопорился на практической реализации, так как красивого отображения придумать не получилось, а простым перебором чудовищно медленно выходит.

force
03.04.2015 13:36+1Я не очень вас понял, но очень похоже, что вы предлагаете что-то похожее, на замену последовательности 12345678 на 11111111, в которой следующий элемент является разницей между предыдущим и текущим. И данное преобразование отлично подходит для сжатия звука, но фигово для сжатия обычных данных.

emreu
03.04.2015 15:27Нет, я не предлагаю кодировать разницу, я предлагаю из уже сжатого потока (у которого распределение по байтам будет равновероятно) выделять блоки фиксированной длинны и преобразовывать их так что распределение будет не равновероятным, а значит их можно будет сжать ещё раз. При этом будет накапливаться дополнительный поток данных, необходимых для обратного преобразования, но объём этого потока будет очень мал, так что в сумме должно получиться меньше чем было изначально.

force
03.04.2015 16:07+1Преобразование Барроуза — Уилера? Которое BWT и используется в bzip2?
Проблема в том, что дополнительный поток данных как раз и сожрёт всю разницу.
emreu
03.04.2015 17:15Судя по тому что есть в википедии это не оно. Я вообще в этой области не специалист, могу сделать только общие прикидки, а проверять практически сейчас времени не хватит, но вот что получается для очень небольших блоков по 64 бита:
для оценки вероятности будем считать что в случайном файле у нас будут встречаться блоки, вероятность появления которых больше 95%, а это блоки с суммой бит от 24 до 40 ( Sum(C(64, k), k=24..40) / 2^64 ~ 0.96). Для записи дельты для этих блоков будет достаточно 4 бит. Наиболее часто встречающиеся блоки с суммой 32 можно отобразить на блоки с суммами от 1 до 27 ( Sum(C(64, k), k=1..27) > C(64, 32)). Таким образом можно уменьшить число «1» бит не менее чем на 5. Если такое преобразование позволит сжать блок до 60 бит, то мы ничего не потеряем. Число перестановок с суммой бит 27 меньше чем 2^60, так что в общем случае мы действительно ничего не должны терять. Однако достаточно велика вероятность отобразить блок так что сумма бит будет мала, значит мы сможем сжать лучше чем в 60 бит и таким образом выиграть на некоторых блоках.
Если брать более длинные блоки, то ситуация может значительно улучшится.
force
03.04.2015 17:33А это уже энтропийное сжатие :) Хаффман, Арифметическое, ренжи.
Хотя вы описали её не в лоб, но вы попадаете на длинный хвост из блоков, вероятность появления которых менее 5%, и которые не сжимаются. А банально за счёт того, что нам где-то нужен флажок, указывающий, «частые блоки»/«редкие блоки», мы на этих редких блоках этим флажком и допинаем всё.
Ну и сразу посмотрите на семейство PPM, это алгоритмы с контекстным моделированием и предсказании. Т.е. они по текущим данным предсказывают следующий блок.
emreu
03.04.2015 17:46Спасибо за информацию! :)
Боюсь только руки не дойдут практической реализацией заняться…

dtestyk
03.04.2015 14:56подвох при таком подходе: всего число вариантов 2^N, случаи N/2+delta более вероятны, потому что их больше, соответственно нужно указать на один из 2^N, можно указать его номер(т.е. не кодировать), или же количество 1 и номер сочетания: sum(С(N,i),i)=2^N
провел немного подсчетов монохромных изображений с одинаковыми гистограммами:
image size: N=w*h
total hists: combin(255, 255+N)
hists with k nonzero bins: combin(k-1, N)
hists corresponding equalized: combin(k, 256)
hists with one image: 256
hists with max images: 1(uniform)
images: 256^N
images of uniform hist: N!/(N/256)!^256

dtestyk
04.04.2015 12:39вот:function count_bits(a){ var n=0 for(var i=0; i<32; i++) n+=(a>>i)%2 return n } function top_bit(a){ var n=0 while(a/=2) n++ return n } n_bits=16 mx=1<<n_bits s=Math.sqrt(n_bits/4)*3 //3 sigma rule s=Math.floor(s) x1=n_bits/2-s x2=n_bits/2+s n_bits_less=0 n_blocks_missed=0 for(z=0; z<100; z++){ a=Math.floor(Math.random()*mx) index=a for(i=a; i; i--) if(count_bits(i)<=x1||x2<=count_bits(i))index-- console.log(a,index, top_bit(a), top_bit(index)) n_bits_less += top_bit(a) - top_bit(index) b=index for(i=1; i<b; i++) if(count_bits(i)<=x1||x2<=count_bits(i))b++ console.log(b) n_blocks_missed += a!=b } console.log('n_bits_less',n_bits_less) console.log('n_blocks_missed',n_blocks_missed)
чудовищно медленно и с большой вероятностью без потерь:)
ILIN-AIC Автор
03.04.2015 13:11Возникла пара вопросов:
«Зафиксировав delta»
Вы имеете в виду сохранение значений дельты, или фиксацию как константы?
«множество которых можно разбить на меньшие множества»
По какому алгоритму Вы производите разбиения?
emreu
03.04.2015 15:14Под фиксацией я имею в виду сохранение значения.
Пусть мы сжимаем блок длинной 1024 бита; посчитали сумму всех его бит, получили 510, соответственно delta=-2, записали её. Далее преобразуем наш блок и получаем блок той же длинны, но не с 510 единичками, а, допустим, с 100. В таком блоке будет совсем другая частота распределения по байтам (уже точно не равновероятная) и его можно будет сжать любым удобным алгоритмом и так же записать в выходной поток. При распаковке мы применяем тот же алгоритм, а потом прочитав дельту отображаем наш блок в 1024 бита с 100 единиц на исходный так, чтобы в результате получился блок с 510 единицами.
Что касается разбиения, то в простейшем случае можно действовать так: перенумеруем все возможные перестановки из K единиц в N позициях, и будем двигаться начиная с первой, проверяя, совпадает ли данная перестановка с нашим блоком. Параллельно будем на каждом шаге генерировать так же перечислимые перестановки с 1 битом «1». Если наша исходная перестановка совпала, то мы заменяем её на сгенерированную. Если мы обошли все сгенерированные перестановки с 1 битом, то начинаем обходить перестановки уже с 2 битами «1» и так далее. Важно что мы обязательно закончим при числе «1» бит меньшем чем в исходной перестановке.
Это самый тупой и медленный алгоритм, но он должен работать.

ILIN-AIC Автор
03.04.2015 15:30Я Вас понял, только непонятно как как Вы делаете вот это:
«Далее преобразуем наш блок и получаем блок той же длинны, но не с 510 единичками, а, допустим, с 100.»
emreu
03.04.2015 16:19Один из возможных способов преобразования я Вам описал выше. Этот способ очень медленный, но он работает. Ничего более изящного и быстрого я не придумал.

realbtr
03.04.2015 13:42+1Проблема определения энтропии большого объема данных в том, что повторяемость данных может быть на очень длинных последователях (сравнимых с самим объемом данных). Например, забавная шутка о том, что белый шум, оказывается, полностью повторяется каждые 2^29 бит

ILIN-AIC Автор
03.04.2015 14:14+1«Проблема определения энтропии большого объема данных в том, что повторяемость данных может быть на очень длинных последователях (сравнимых с самим объемом данных).»
Может быть я вас не совсем понял, но чем длиннее последовательность тем реже она повторяется в высокоэнтропийных данных.
Шутка про повторяемость белого шума напоминает нам о том что любая самая длинная последовательность бинарного кода с длиной n с вероятностью 50 процентов опять встретится на отрезке не превышающем 2*n*(2^n), где ^ — знак возведения в степень. Т.е. фрагмент белого шума из вашей шутки что такое повторяемостью не превышает 29 бит.
Ближе к теме обсуждаемой статьи, в принципе каждый может проделать простой эксперимент. Взять достаточно небольшой фрагмент высокоэнтропийного двоичного кода (если такового под рукой нет — то просто подкинуть монетку сто раз записать результат в виде нулей и единиц). Затем в одной копии этого кода сделать замену «00» на знак «2», а в другой копии этого кода сделать замену «01» на тот же знак «2». Даже на отрезке в 100 бит будет видна существенная разница между количеством найденных и замененных сочетаний «00» и «01».
realbtr
03.04.2015 16:54Смысл в том, что мы можем лишь вероятностно утверждать, что длинных повторяющихся последовательностей — нет. А вот проверить это в любых конкретных данных — задача непростая.
Которая еще больше усложняется, если, по сути, повторяются не сплошные, а перемежающиеся последовательности. Да еще и не прямо, а самоафинно.
По сути дела, можно сгенерировать такой многогигабайтный файл с данными, который статистически будет представлять собой белый шум, а модель его генерации будет заключаться в каких-нибудь несчастных паре килобайт. При этом, не используя стохастичности (т.е. генерация абсолютно устойчивая).
Разумеется, это гипотеза (ее можно доформулировать до теоремы и доказать, но на полях, как известно, мало места...)

saboteur_kiev
03.04.2015 14:11Основная проблема такого множественного сжатия (не буду говорить бесконечного) в том, что на практике оно невыгодно. Количество энергии потраченное на сжатие небольшого процента информации выйдет дороже чем приобретение лишнего носителя или развития текущих технологий записи, в которых скачок не в 1%, а например в два-три раза вполне достижим, что практически подтверждается.
Поэтому подобными вопросами занимаются весьма поверхностно — на уровне идеи и простых моделей. Но до успешного продукта (я не говорю про коммерческий), а просто, которым будут реально пользоваться — врядли дойдет…
P.S. В детстве тоже моделировал варианты, как можно сжатые данные подвергнуть какой-то известной переработкой, чтобы уменьшить энтропию. И до сих пор думаю, что может быть там что-то и есть.
Например, была вот такая достаточно рабочая идея с ощутимым выхлопом:
Публичный словарь для сжатия.
То есть в отдельно взятом онлайн хранилище, хранятся проиндексированные длинные последовательности различных данных.
Архиватор сжимает файл, используя этот словарь.
Таким образом ЛОКАЛЬНО, данные сжимаются, и сам архиватор не обязан локально хранить словари.
Минус — необходим доступ к этому хранилищу онлайн, возможно быстрый канал связи.
Плюс — словарь на планете хранится один раз (ну несколько с зеркалами).
Словарь может содержать различные последовательности для различных типов данных, со временем будет обучаться и количество последовательностей становиться больше. Даже бизнес на этой идее можно сделать неплохой. Но врядли сейчас.
IMHO идея обязательно будет когда-нибудь воплощена, но вряд ли мной :(
ILIN-AIC Автор
03.04.2015 14:24-1«Основная проблема такого множественного сжатия (не буду говорить бесконечного) в том, что на практике оно невыгодно. Количество энергии потраченное на сжатие небольшого процента информации выйдет дороже чем приобретение лишнего носителя или развития текущих технологий записи, в которых скачок не в 1%, а например в два-три раза вполне достижим, что практически подтверждается.»
То есть на одной чаше весов все дата-центры мира со всей потребляемой ими энергией, а на другой микрочип в котором содержится вся информация находящаяся в этих дата-центрах. И вы утверждаете что такой микрочип энергетически невыгоден?
Я как раз предлагаю вместо массивных дата-центров иметь такие микрочипы куда можно уместить какое угодно количество данных. Этакий дата-центр у каждого в кармане, с месячным бэкапом мирового интернета.
saboteur_kiev
03.04.2015 14:28Вы мухлюете с подменой понятий.
Какое количество энергии нужно потратить, чтобы расшифровать информацию из микрочипа, если для ее шифрования/дешифрования надо сделать хреналиард проходов?
Мое решение — не затрагивает процессорное время, то есть скорость сжатия/разжатия не равна, но хотя бы сравнима с обычными архиваторами. Но при этом, за один проход сжатия, метод использования публичных словарей дает ощутимый прирост. А в некоторых случаях, даже больше чем обычные архиваторы.
От массивных дата-центров все равно никуда не деться, так почему бы не использовать один под словари.
ILIN-AIC Автор
03.04.2015 14:39Из всего что есть в вашем комментарии мне больше всего понравилось слово «хреналиард». Рассматриваю его как бренд для будущего поисковика ;)
Разжимать придется во первых не весь архив, а какую-то его малую часть используя иерархическую структуру данных. А затем, в конце концов, кто мешает этот ваш словарь поместить в каждый микрочип? Вот вам и экономия электроэнергии на каналах связи.
saboteur_kiev
03.04.2015 15:15Мне мешает то, что словарь тупо не влезет в каждый микрочип.
Под словарем я подразумеваю «длинные последовательности различных данных», а не просто какие-то слова русского или английского языка. И ее длина может быть велика.
То есть весь смысл такого хранилища — хранить как раз те самые хаотические куски данных, сжатие которых обычными методами уже не имеет смысла.
P.S. хреналиард — это не совсем то слово, которое я имел ввиду, но то слово слишком нецензурное, хотя звучит лучше ;)
ILIN-AIC Автор
03.04.2015 15:24«Мне мешает то, что словарь тупо не влезет в каждый микрочип»
В мой влезет ;)
P.S. Тогда «хреналиард» беру во временное пользование :)

mrThreeElephants
03.04.2015 14:47+1Публичный словарь для сжатия.
То есть в отдельно взятом онлайн хранилище, хранятся проиндексированные длинные последовательности различных данных.
Архиватор сжимает файл, используя этот словарь.
Так постойте я кажется знаю такой словарь. И такой «архиватор».
Он называется BitTorrent. Как говорят на башорге «крупнейший восстановитель файлов по md5-сумме».
Словари не хранятся локально. magnet-ссылка меньше dvd-образа фильма в 100500 раз.
Вопрос только в том можем ли мы, пользуясь моделью черного ящика считать процесс скачивания торрента «распаковкой», а процесс создания magnet-линка «сжатием»?
И не путаем ли мы тут архивацию с индексацией?
ILIN-AIC Автор
03.04.2015 14:59Несколько гипертрофированно, но безусловно есть определенное сходство…

mrThreeElephants
03.04.2015 15:30Возможно и гипертрофированно но вопросы тем не менее остались в воздухе.
Имеем ли мы право считать процесс скачивания торрента распаковкой magnet-линка?
Мне кажется тут имеет место вопрос контекста распаковки данных. Мы не храним в торрентах видео телевизионных помех. Все возможные комбинации телевизионных помех. Мы не храним торрент-раздачах видео вторжения марсиан… а, нет храним. Ну не важно.
Суть в том что задача алгоритма архивации в том чтобы сжать данные в принципе а задача торрент-сети обмен достаточно ограниченным количеством файлов.
Говоря «ограниченным» я имею в виду ограниченным относительно количества всех возможных комбинаций единиц и нулей в рамках файла размером, скажем в 1 гигабайт (около 2^1073741824 вариантов одного файла если я не ошибаюсь).
То есть определяя область, если можно так выразиться, допустимых значений для задачи сжатия файлов мы существенно упрощаем задачу алгоритмам архивации.
Пусть M — область всех возможных комбинаций нулей и единиц в самом большом в мире файле.
N — общее количество файлов с уникальным содержанием на хардах всего человечества.
И T — подмножество N — все те файлы которые когда-либо были опубликованы в сети torrent.
Очевидно что M >> N >> T
Поскольку задачей торрент сети является отображение всего лишь ЧАСТИ множества N на множество T то понятно откуда такая эффективность в «сжатии» (если можно так выразиться).
ILIN-AIC Автор
03.04.2015 15:44«Возможно и гипертрофированно но вопросы тем не менее остались в воздухе.
Имеем ли мы право считать процесс скачивания торрента распаковкой magnet-линка?»
Да поскольку в принципе все существующие способы сжатия данных делают нечто иное как обычную табличную замену — отсюда и энтропийное ограничение Шеннона
Я пытаюсь объяснить уважаемому сообществу, что речь идет о принципиально ином подходе к сжатию данных — алгоритмическому.
Это как если бы мы вместо сжатия 3 миллиардов знаков числа пи просто написали бы программу для их вычисления. Которая, конечно, будет существенно короче этих трех миллиардов знаков.
Идея эта придумана и обоснована не мной. Вопрос был в том чтобы написать универсальную программу которая исходные данные с максимальной энтропией (то есть несжимаемые современными программами сжатия) записывала бы в более короткий цифровой код.

saboteur_kiev
03.04.2015 15:20-1Ну, проблема в том, что в вашем случае, если кто-то заранее не закинул туда файл целиком, то восстановить его не выйдет.
Самое главное, что идея — в принципе рабочая. Не сейчас и возможно не в ближайшие 10 лет, но рабочая.
Некоторые могут реализовать что-то подобное внутри компании.
А путать архивацию с индексацией — собственно индексация это тоже один из используемых в архивировании алгоритмов.
mrThreeElephants
03.04.2015 15:39Ну в случае с архиватором такая ситуация тоже возможна: если сгенерировать случайную последовательность вместо данных с архивом то распаковать его не выйдет. Или если все сжать нормально но, потом разбить архив на части и половину частей потерять (помните winrar?)
Идея — да, действительно рабочая ее Amazon уже применяет в сервисе Work Ops (вроде) для обновления нод кластера через torrent.
saboteur_kiev
03.04.2015 15:55Подозревал, что уже где-то будущее уже наступило!
Но что-то я не совсем понял… Обновление нод кластера через торрент и использование внешних словарей — разные вещи.

equand
03.04.2015 15:39Нет Bittorrent немного не то,
Нужен blockchain с рандомными данными в блоках по 16 байт. Будет весить 18.45 эксабайт :D.
В итоге сэкономим в 16 раз весь глобальный траффик и данные.
saboteur_kiev
03.04.2015 15:57не в 16, на индекс уйдет больше 1 байта. Но можно блоки сделать длиннее.
Насчет трафика — некоторые умные маршрутизаторы и модемы уже умеют составлять свои собственные словари часто передаваемых цепочек данных, и если внутренняя память позволяет, то переданный один раз файл размером в гигабайт, в следующий раз будет передан за мгновение, если память не будет занята под другие данные.
Возможно такой вариант с публичным словарем заинтересует глобальных провайдеров межконтинентальных и междугородних магистралей, задолго до внедрения в массы.
equand
03.04.2015 16:03То что Вы называете — это кеширование. Bittorrent — пиринговая сеть. То о чем я говорю — это заранее поставляемое ПО (возможно в виде чипа), которое работает как дешифратор (есть блоки, сортированы по а-я, индекс — его позиция в сортировке). Хотя в принципе можно и качать его из интернета (по индексу).

Deranged
03.04.2015 14:42Я вообще, довольно плохой философ, поэтому вопрос наверное тупой. Но вот вопрос.
Допустим, я хочу сжать файл 100500Гб. И так уж совпало, что всё его содержимое (не суть, в кодах ASII или HEX) совпадает с цифрами числа Pi, начиная с 549760232349346-го знака. Это значит, что я могу «сжать» файл в комбинацию — иррациональное число + позиция + длина.
Не противоречит ли сам факт такой возможности теореме Шеннона?
mrThreeElephants
03.04.2015 15:03Тут когда-то статья была про файловую систему которая данные хранит в числе пи (статью сходу не нашел, к сожалению). Автор предупреждал что работает медленно. :)
Сжать файл-то вы таким образом конечно можете — но вопрос в том где именно в пи он встретится (помним что чем длиннее последовательность — тем меньше вероятности ее встретить), и не будет ли смещение (число) по размеру длиннее чем сам файл?
И сколько вычислительных ресурсов потребуется чтобы вычислить пи до такого знака?
ILIN-AIC Автор
03.04.2015 15:08Да дело даже не в вычислительных ресурсах (с таким же успехом места вычисления числа pi можно использовать генератор случайных чисел), а в том что указание места где встречается эта последовательность в большинстве случаев будет длиннее самой последовательности :(

ILIN-AIC Автор
03.04.2015 15:05-1Вы совершенно правильно задали вопрос. Теорема Шеннона с ее ограничениями верна только для статистического или комбинаторного сжатия (Колмогоров в своей статье «Три подхода к определению понятия „Количество информации“» показал идентичность этих двух подходов). Как перспективное направление он указал алгоритмический подход к обработке данных. О чём и идёт речь в обсуждаемой нами статье.

equand
03.04.2015 15:42Теоритически с помощью квантового компьютера можно было бы вычленять локацию в pi.

0serg
03.04.2015 14:42+7Джентельмены, как можно всерьез обсуждать сжатие случайных данных? Сегодня же не первое апреля!
Пусть A — пространство всех возможных сообщений, B — пространство составленное из соответствующих «архивов».
Архиватор каждому сообщению a (элементу A) ставит в соответствие сжатую версию b (элемент B)
Разархиватор напротив, по b (элементу B) позволяет найти соответствующий A.
Очевидно что разным a соответствуют разные b и наоборот, т.е. архивирование задает биекцию (взаимно-однозначное отображение) множества A на B
Давайте рассмотрим в качестве A все возможные сообщения длины не более N бит. Существует ровно 2^{N+1}-2 таких сообщений, следовательно у нас должно быть ровно 2^{N+1}-2 разных элемента в множестве B.
Предположим теперь что все сообщения являются равновероятными (сжимание случайных данных). Попробуем посмотреть насколько может сжать такие данные самый лучший из возможных архиваторов.
Лемма: пусть некоторые сообщения в B имеют длину M бит. Тогда если B не содержит в себе всех возможных битовых последовательностей длиною меньше M бит, то архиватор не оптимален
Доказательство: берем сообщение длиной M бит и заменяем его на неиспользованную последовательность из <M бит. Т.к. она неиспользованная, то биекция не нарушена, мы сможем восстановить исходное сообщение. При этом мы улучшили сжатие архиватора на одном сообщении не ухудшив его ни в одном другом.
Следовательно оптимальный архиватор должен использовать в B все возможные битовые последовательности длины не более M бит для некоторого M и все сжатые сообщения этого архиватора будут иметь длину не более M+1 бит. Каково же может быть значение этого M? Поскольку существует всего 2^{M+2}-2 разных сообщения из M+1 бита, M должно быть достаточно велико чтобы все заархивированные сообщения были различными: 2^{M+2}-2 >= |B| = |A| = 2^{N+1}-2. Отсюда очевидно M+2>=N+1 или M >= N-1.
Минимально возможное M таким образом = N-1. Но вот незадача — легко посчитать что при таком M множество B исходя из той же логики равной мощности должно включать в себя не только все возможные последовательности из N-1 бита, но и все возможные последовательности из N бит. Приплыли — «идеальный» архиватор заведомо переводит все возможные сообщения из не более N бит в… все возможные сообщения из не более чем N бит. Если все исходные события равновероятны, то все кодированные сообщения тоже равновероятны, и следовательно средняя длина сжатой последовательности у идеального архиватора в точности равна средней длине исходной :)
Вы никуда не можете уйти от этих элементарных ограничений на A и B. ВСЕ реальные архиваторы вынуждены опираться на то что в реальных сообщениях исходные элементы A далеко не равновероятны и ВСЕ они работают по принципу «сортировки» когда отсортированные по убыванию вероятности сжатые сообщения в B имеют (в идеальном случае) строго возрастающую битовую длину. Это дает возможность для любого заданного наперед словаря сообщений A с известными вероятностями определить идеальный архиватор B, обогнать который невозможно: все возможные сообщения в A просто сортируются по вероятности их появления и N-му по вероятности появления сообщению ставится в соответствие число N в бинарной записи. Другой вопрос что на практике он в большинстве случаев не применим и приходится идти на разные ухищрения чтобы к нему приблизиться :).
ILIN-AIC Автор
03.04.2015 14:56-1«Джентельмены, как можно всерьез обсуждать сжатие случайных данных?»
Я вижу что джентльмен не читатель :) Выше уже обсуждалась это ваше доказательство которое верно только для существующих способов сжатия данных.
В обсуждаемой статье предлагается совершенно иной подход (алгоритмический) к сжатию данных, которые вполне серьезно рассматривался и обсуждался, например, таким авторитетным математиком как Колмогоров. Выше я цитировал его общие выводы относительно такого подхода и приводил ссылку на его фундаментальную статью, которую специально повторяю для всех таких джентльменов:
Колмогоров А.Н. Три подхода к определению понятия «Количество информации» см. §3 Алгоритмический подход
compression.ru/download/articles/ti/kolmogorov_1965_three_way_pdf.rar
Если Вы не согласны с выводами Андрея Николаевича, и есть что возразить по сути — милости прошу…
chersanya
03.04.2015 15:34+5Вы бы по сути возразили :) 0serg всё правильно написал, не важно какая процедура сжатия — любой файл она сжать не сможет.
Укажите, с какими пунктами вы не согласны здесь:
- файлов длины N всего 2^N
- файлов длины меньше N всего (2^N)-1
- т.е. файлов длины N больше, чем всех более коротких файлов
- следовательно никакой процедурой нельзя взаимооднозначно сопоставить одни другим (это и значит, что нельзя сжать все файлы)

ILIN-AIC Автор
03.04.2015 15:58«Вы бы по сути возразили :)»
Так он по сути моего алгоритма никаких возражений не привел. Это как если бы человеку показали самолет, а он бы обосновал, что аппарат тяжелее воздуха не может летать. ( кстати реальный исторический факт)
«Укажите, с какими пунктами вы не согласны здесь:
файлов длины N всего 2^N
файлов длины меньше N всего (2^N)-1
т.е. файлов длины N больше, чем всех более коротких файлов
следовательно никакой процедурой нельзя взаимооднозначно сопоставить одни другим (это и значит, что нельзя сжать все файлы)»
Со всеми пунктами согласен. Тут дьявол кроется в деталях. У моего оппонента речь идет «взаимооднозначном сопоставлениии», которое имеет место быть в статистическом или комбинаторном сжатии.
При алгоритмическом сжатии речь идет об создании программы воспроизводящей сжатые данные, причем запись этой программы должна быть короче самих сжатых данных.
Это как если бы мы вместо сжатия 3 миллиардов знаков числа пи просто написали бы программу для их вычисления. Которая, конечно, будет существенно короче этих трех миллиардов знаков.
chersanya
03.04.2015 16:06+3Да какая разница, какое именно у вас сжатие. Ну и что, что вы предлагаете создавать программу, которая воспроизведёт данные? Программ размером меньше N всё равно меньше, чем файлов размером N.
По поводу алгоритма — я вот хотел указать на ошибки по сути, но в таком виде это достаточно сложно. Если можно, опишите пожалуйста алгоритм более строго, в частности место где говорится
Стало быть, в полученном фрагменте для восстановления первоначального состояния нужна информация только о расположении одного знака “2”, т. к. очевидно, что другая двойка обязательно должна будет расположена после первого знака в сочетании
, ну и весь этот абзац вообще :)
А ещё лучше, показали бы реализацию, все вопросы и отпали бы :) Длинная арифметика сейчас почти во все языки встроена, выбор на чём писать огромный.
С числом пи вообще не понял, к чему — его цифры ну никак не являются несжимаемой последовательностью, о чём вы собственно и сказали.
ILIN-AIC Автор
03.04.2015 16:27«С числом пи вообще не понял, к чему — его цифры ну никак не являются несжимаемой последовательностью, о чём вы собственно и сказали.»
Начну с конца. Последовательность цифр числа пи является данными энтропия которых максимальна. Возьмите например 3 миллиона двоичных знаков числа пи и попробуйте сжать любой существующей программой сжатия. Получить результат меньше трех миллионов бит (или 375000 байт) у Вас не получится.
Гораздо короче просто сохранить программу которая воспроизводит путем вычисления эти три миллиона ( или хоть 3 миллиарда) двоичных знаков.
«Стало быть, в полученном фрагменте для восстановления первоначального состояния нужна информация только о расположении одного знака “2”, т. к. очевидно, что другая двойка обязательно должна будет расположена после первого знака в сочетании»
Речь идет о том что для выбранного АКС «101» когда мы его заменили в бинарном коде на любой другой знак например 2, существует ограничение — он не может стоять справа после последовательности «10» ( если замена АКС происходила слева направо).
Например: была последовательность 10101, если мы слева направо заменяем АКС «101» на другой знак, например 2, у нас никак не может получиться в результате 102, а только 201. Поскольку при замене слева направо программа сначала находит первые три знака которые соответствуют АКС «101»01 затем оно заменяет их на другой знак — в нашем случае на 2: «101»01 -> «2»01.
В этом случае преобразование последовательности 10101 в 102 исключено, поскольку для этого нам пришлось бы пропустить первые два знака.
chersanya
03.04.2015 16:38+1Вы кажется описали следующий абзац за тем, на который я указал.
А про число пи — ну и что, что энтропия максимальная? Она же учитывает только частоты цифр, и всё. Даже оставим в стороне то, что энтропия рассчитывается не для конкретного числа, а для источника случайных чисел.
Причём здесь «любые существующие программы сжатия» — тоже не понятно. Обычно архиваторы делают для того, чтобы сжимать данные, которые часто встречаются в реальности, ну а сжатие числа пи очень редкая операция — поэтому ничего удивительного, что с ней справляются плохо.
Ясно же, что любую последовательность цифр длины N любого вычислимого числа можно закодировать O(log N) битами (да-да, написать программу, которая его выводит :)).
sergeyII
03.04.2015 16:57Если количество программ по определению меньше, чем вариантов того, что они должны вывести, то можно предложить наплодить великое множество разнообразных процессоров, на которых они будут выполняться. Как вам такой разворот? :)

lair
03.04.2015 17:43+1При алгоритмическом сжатии речь идет об создании программы воспроизводящей сжатые данные, причем запись этой программы должна быть короче самих сжатых данных.
Знаю я одну такую запись. Называется «нотная».
Знаете, в чем ее проблема?

rg_software
03.04.2015 22:08+5Вот же забодали с этим аппаратом тяжелее воздуха. Вы можете привести доказательство, которое приводилось в этом реальном историческом факте?
Каким бы оно ни было, это «доказательство» — неверное, и я не понимаю, с какой целью регулярно в дискуссиях любят ссылаться на некоторую попытку с ошибкой доказать чего-либо.
В то время как доказательство вашего оппонента корректно, и чем ссылаться на самолёты, найдите ошибку.
Вы пытаетесь доказать, что сжатие A в B и создание программы, которая генерирует A — это разные вещи. В действительности это одно и то же: вот есть самораспаковывающися архив RAR с расширением .exe, и как он работает внутри — «генерирует» А или «распаковывает» А из B в данном случае неважно, теорема работает в любом случае.
Единственный аргумент в пользу вашей теории может состоять в том, что все «распаковщики-генераторы» будут опираться на некую универсальную библиотеку фрагментов, присутствующую на всех компьютерах пользователей. Вот ниже приводят пример нотной азбуки. Если у меня стоит хорошая библиотека инструментов, MIDI-композиции могут звучать на моём компьютере гораздо красивее, чем у соседа с FM-чипом.
Но это в целом достаточно сомнительная линия рассуждений, да и вообще по сути чит.

0serg
04.04.2015 21:21+2Это доказательство верно для *любых* способов сжатия данных подразумевающих запись входных и выходных сообщений в виде некоторой последовательности битов, поскольку оно опирается только на два очевидных соображения:
* разным входным последовательностям соответствуют разные архивы
* число различных последовательностей заданной битовой длины ограничено определенным числом
Если угодно, это «закон сохранения энергии» применительно к сжатию данных
Понятие колмогоровской сложности мне прекрасно известно и Колмогоров, естественно, не пытается доказывать тезис который вы ему приписываете. Где в цитируемом Вами документе, на какой странице содержится на ваш взгляд это утверждение?

saboteur_kiev
03.04.2015 16:00-3«Джентельмены, как можно всерьез обсуждать сжатие случайных данных? Сегодня же не первое апреля!»
Математически — нельзя. Практически можно.
Просто потому, что если правильно расставить приоритеты, то можно найти другие подходы к решению проблемы.
Суть не всегда в том, что вот есть кусок данных и его нужно сжать. Суть часто бывает в том, что есть кусок данных и его нужно «ужать» в нужное место или «передать другое место как можно быстрее». И тут начинаются 1 капля + 1 капля = 1 капля.
0serg
04.04.2015 21:38Я не совсем понял Вашу мысль, простите. Обычно чем битовые последовательности короче, тем их и впихнуть куда-то проще, и тем передать их можно быстрее.

saboteur_kiev
06.04.2015 11:55Несколькими страницами выше я привел пример идеи, которая может сработать. Подразумевается публичный словарь неких цепочек данных, которые можно использовать для сжатия/разжатия.
Таким образом, этот словарь находится не у пользователя, он хранится один раз, следовательно чем больше пользователей — тем чаще использованы цепочки данные. Это не «теоретический математический подход» к сжатию данных, это использование публичных мест для хранения цепочек, которые уже нельзя сжать.
Если провести детальный анализ множества сжатых данных и выбрать максимально часто встречающиеся цепочки, то из набора можно смело исключить все повторения и последовательности, в которых есть некая система — такие цепочки уже будут сжаты обычными методами. Из оставшихся можно будет выбрать некоторое количество часто встречающихся, чтобы на их индексирование ушло меньше бит/байт.
Да, огромный минус, что без подключения к сети, нельзя будет ни запаковать ни распаковать, и пока еще несовсем ясна модель монетизации, чтобы такое хранилище цепочек могло надежно существовать. Но идея, на первый взгляд, рабочая.
0serg
06.04.2015 12:50+2Для случайных данных никакой словарь работать не будет, см. доказательство выше — оно допускает наличие какого угодно словаря. Тот «теоретически идеальный метод сжатия» который там описан, собственно, потому и неприменим на практике что требует нереально огромного словаря.
Неслучайные данные можно сжимать и можно искать для них эффективные словари. Это называется «preset dictionary» и поддерживается рядом существующих библиотек и форматов сжатия. На практике выигрыш дает только на очень маленьких данных, на сколь-либо больших последовательностях неэффективно, потому особого распространения практика не получила.

dtestyk
03.04.2015 15:44Если честно, не понял оригинальный алгоритм в статье. Но думаю, что «кодирование» заданием проверяющей функции и некоторых эвристик позволит перевести память для хранения во время «декодирования» перебором с применением соответствующих эвристик. Например, для изображений можно указать высокоуровневые признаки(наличие кота, лица...), хеши, номер решения и какой-то алгоритм перебора, гарантирующий декодирование.

chersanya
03.04.2015 15:59+1Многие так думают, но в общем случае это невозможно. Либо в среднем набор хранимых признаков имеет длину не меньше, чем исходные данные, либо будет неоднозначное декодирование. Ничего не поделаешь :)

dtestyk
03.04.2015 17:41Возможно, но никто не мешает поставить задачу сжатия в более общем виде: построить алгоритм сжатия
Например, последовательность псевдослучайных чисел можно сжать до алгоритма их генерации, который, как правило, короче самой последовательности
в среднем набор хранимых признаков имеет длину не меньше
Наличие признака должно сокращать число вариантов. Например, «на фото лицо крупным планом на зеленом фоне», сразу отпадает огромное число вариантов. Если признака нет, не нужно его и указывать.
chersanya
03.04.2015 17:59+1Это всё хорошо, но вы посмотрите на это с другой стороны. Не важно, как назвать данные, по которым потом восстанавливается исходник — архивом или признаками (всё равно ведь хранятся в виде файла). Суть в том, что суммарная длина этих данных в среднем будет не меньше, чем исходника.
Да, сгенерированные некоторым алгоритмом числа можно сжать до этого самого алгоритма. Но алгоритмов (программ) меньшей длины опять-таки меньше, чем вариантов исходных данных :)
dtestyk
03.04.2015 18:14потенциально да, но врядли кто-то будет пробовать сжимать все возможные варианты даже килобайтных файлов :)

NYMEZIDE
03.04.2015 15:54Идея конечно интересная — но пока у нас не квантовые компьютеры. Которые будут способны перебрать все данные и увидеть супер формулу закономерности этих данных.
Представляю себе как построят супер компьютер — дадут ему данные для сжатия — он будет 100 лет работать — а потом выдаст ответ: 42

ILIN-AIC Автор
03.04.2015 16:02«Идея конечно интересная — но пока у нас не квантовые компьютеры. Которые будут способны перебрать все данные и увидеть супер формулу закономерности этих данных.»
В том-то все и дело, что пришлось все это сделать без квантовых компьютеров. Закономерность эта уже найдена, и об этом собственно статья.
NYMEZIDE
03.04.2015 16:10Ткните меня в носом в эту закономерность всего всего. Я ее не увидел. или 101, 010 = 2 это и есть закономерность?
Мне это напоминает тарелку с манной кашей и вареньем. Вначале каша и варенье были отдельно. Потом их соединили и ложкой смешали до однородной массы. Мы знаем как мешали, сколько раз по часовой стрелке и против часовой и под каким углом и т.д. НО сможем ли мы мешая обратно — восстановить первоначальные состояния каши и варенья? Ответ — нет.
или воспроизвести тоже самое состояние — имея тот же объем каши и варенья, туже самую ложку и т.д., мешая точно также как мы мешали первый раз?
ответ — ?
ILIN-AIC Автор
03.04.2015 16:38Про манную кашу и варенье у вас получилось несколько провокационно. Кажется пора подкрепиться… © Винни-Пух
А что касается закономерностей в хаосе — кто их значительно больше, я привел пример самой простой (101 или симметричная ей 010).

zvorygin
03.04.2015 16:42+1Шикарное видео про разделение «каши» и «варенья» — www.youtube.com/watch?v=LwrJp7G7KsI

miwa
03.04.2015 16:37Немного не в тему, но все же. Вы в курсе, что вместо «миллиардов гигабайт», «триллионов гигабайт» и прочего словесного мусора существуют более короткие и общепонятные (как минимум на хабре) терабайты, петабайты и т.д.?

zvorygin
03.04.2015 16:39+2Предлагаю автору супер способ сжатия любых данных в два раза:
Заменяем 00 на 1, 01 на 2, 10 на 3, 11 на 4.
Вуаля, из строки 0110 1100 1001 1110 мы получаем 23413243.
А выше уже правильно говорили про биекцию.

ILIN-AIC Автор
03.04.2015 16:46Мне просто интересно — а после того как будет представлена работающая программа сколько пройдет времени пока джентльмены поймут, что они были не правы :)

NYMEZIDE
03.04.2015 16:551. жду программу которая разожмет файл с каким-то полезным контентом — фильмом например, размером 4-4,5 Гб (DVD)
2. жду архив, который будет весить меньше либо равно 1 Мб.
3. Хочу получить этот фильм. (путем запуска этой программы и указания ей архива)
Если фокус на машине, без интернета (не хочу битторент качалку получить вместо чудо программы) — получу фильм — признаю свою неправоту и даже готов пожертвовать небольшую сумму для развития такого чудо архиватора, думаю другие тоже скинуться.
Сколько вам нужно времени? )
ILIN-AIC Автор
03.04.2015 17:04Учитывая то на чём я программирую, пока могу предложить только 10 мегабайтный архив (например rar) сжатый раза в два. И программу к нему не более мегабайта. Учитывая что за один проход происходит сокращение данных на около 0.005 %, то сжатие в 2 раза — это более 13862 циклов. Сколько это займет по времени пока сказать не могу…

chersanya
03.04.2015 17:06А есть у алгоритма минимальный размер данных? Если нет, то предлагаю сжать 1 бит данных, если есть — то берите минимальный размер, быстрее будет :)

sergeyII
03.04.2015 17:26Бит сложно сжать, вот мне вчера скинули пароль — там всего два байта, было бы неплохо сжать два байта в один — вот это я понимаю тз…

lair
03.04.2015 17:47Сколько это займет по времени пока сказать не могу…
Тогда откуда вы знаете, что ваше решение работает?

ILIN-AIC Автор
03.04.2015 21:48Я просто знаю сколько длится 8-10 циклов (оставлял комп работать на ночь ;)

lair
03.04.2015 22:26Так откуда вы знаете, что ваше решение работает? Где, скажем, математическое доказательство корректности и вычислительной сложности?

lair
03.04.2015 22:28Я вам больше того скажу. Чтобы показать работоспособность вашего алгоритма, достаточно сделать два простых теста. Оба из них получают на вход случайную (т.е., каждый раз меняющуюся) последовательность байт. Первый прогоняет ваш алгоритм и демонстрирует, что размер уменьшился. Второй — прогоняет ваш алгоритм в две стороны и сравнивает результат со входными данными.
Кстати, ваш алгоритм детерминистический?
ILIN-AIC Автор
03.04.2015 22:55-1Чтобы показать работоспособность нашего алгоритма, достаточно просто выложить самораспаковывающийся архив, внутри которого сжатый в 2 раза rar файл мегабайт на 20, внутри которого в свою очередь содержится полезная информация. Причем такой rar файл другими архивами сжиматься уже не должен.
Речь как раз и идет об ускорении работы программы.
По второму вопросу детерминирован ли данный алгоритм пока сказать трудно. Надеюсь не начнут проявляться никакие квантовые эффекты ;)
lair
03.04.2015 22:59+2Чтобы показать работоспособность нашего алгоритма, достаточно просто выложить самораспаковывающийся архив, внутри которого сжатый в 2 раза rar файл мегабайт на 20,
Зачем на 20? Почему нельзя с двух килобайт начать?
Ну и да, это не докажет работоспособность алгоритма, это докажет, что есть файл, который им сжимается. Но вы-то говорите о применимости к любым данным.
детерминирован ли данный алгоритм пока сказать трудно
То есть вы сам не знаете, от чего зависит поведение вашего алгоритма?
ILIN-AIC Автор
03.04.2015 23:26-1Зачем на 20? Почему нельзя с двух килобайт начать?
Вы невнимательно читали статью из которой следует, что за один проход сокращение данных происходит на 0.00005. То есть для 2 килобайт или 2048 бит сокращение должно составить 0.1024 бит. Таких ячеек памяти я еще не придумал. Минимум 1 бит. А стало быть теоретически пока сжатие достижимо только для 20 тысяч бит. Но это только теоретически поскольку существует еще служебная информация ( некоторые указания относительно параметров конкретного файла а это еще минимум 30 — 50 бит), что ещё в свою очередь повышают минимальный размер сжимаемого файла в 50 раз — уже миллион бит то есть грубо говоря где-то 125000 килобайт которые в лучшем случае мы сможем сократить даже не на байт, а на бит. Для сокращения данных на байт потребуется сжимать почти мегабайт, и это пока для данного алгоритма минимальный размер блока для сжатия.
То есть вы сам не знаете, от чего зависит поведение вашего алгоритма?
Да нет это просто под конец дня так шучу. Конечно алгоритм
детерминирован. Это же не искусственный интеллект который рассуждает: Сжать или не сжать вот в чем вопрос?
lair
03.04.2015 23:34+1Вы невнимательно читали статью из которой следует, что за один проход сокращение данных происходит на 0.00005.
Математическое обоснование можете предоставить?
То есть для 2 килобайт или 2048 бит сокращение должно составить 0.1024 бит.
Вы серьезно не в курсе, что 2 килобайта — это 16384 бита?
Но это только теоретически поскольку существует еще служебная информация ( некоторые указания относительно параметров конкретного файла а это еще минимум 30 — 50 бит),
Это что это за информация такая?
что ещё в свою очередь повышают минимальный размер сжимаемого файла в 50 раз
Это как это 30-50 бит служебной информации — которая, кстати, должна быть константой и легко вычитаться — повышают минимальный размер файла в 50 раз?
уже миллион бит то есть грубо говоря где-то 125000 килобайт которые в лучшем случае мы сможем сократить даже не на байт, а на бит.
Я хочу заметить, что миллион бит — это 125 тысяч байт, а не килобайт, так вы утверждаете.
Для сокращения данных на байт потребуется сжимать почти мегабайт, и это пока для данного алгоритма минимальный размер блока для сжатия.
Прекрасно. Начните с мегабайта. Зачем двадцать-то?
Кстати, так какая у вашего алгоритма асимптотическая сложность — иными словами, во сколько раз быстрее он обрабатывает один мегабайт, чем два?
ILIN-AIC Автор
03.04.2015 23:56Математическое обоснование можете предоставить?
Обязательно но попозже
Вы серьезно не в курсе, что 2 килобайта — это 16384 бита?
2*8*1024=16384 Я в курсе просто спать хочу :) И мозги плохо работают…
Это что это за информация такая?
Ну такая особая секретная информация ;) Например имя сжатого файла, которое может отличаться от имени архива
Это как это 30-50 бит служебной информации — которая, кстати, должна быть константой и легко вычитаться — повышают минимальный размер файла в 50 раз?
Запросто:
1/0.00005=20000
(1+50)/0.00005=1020000
Я хочу заметить, что миллион бит — это 125 тысяч байт, а не килобайт, так вы утверждаете.
Это просто грубая прикидка, а отнюдь не попытка ввести Вас в заблуждение. Признаю на самом деле 122.0703125 килобайт.
Прекрасно. Начните с мегабайта. Зачем двадцать-то?
То есть если я сожму мегабайт на 1 байт это лично Вас убедит? Однако боюсь что остальную уважаемую публику это отнюдь не впечатлит.
Кстати, так какая у вашего алгоритма асимптотическая сложность — иными словами, во сколько раз быстрее он обрабатывает один мегабайт, чем два?
Извините честно говоря засыпаю и соображаю с трудом. Боюсь вам неправильно ответить

lair
04.04.2015 00:06Обязательно но попозже
Вообще-то с него начинать надо.
Например имя сжатого файла, которое может отличаться от имени архива
Для целей доказательства это не нужно — сжимается байтовый массив в байтовый массив. И, кстати, имя файла в 50 бит вы не поместите: 50 бит — это 6 с мелочью байт, порядка трех символов.
Ура, мы только что выкинули 50 бит из рассмотрения, можно уменьшать размер сжимаемого файла обратно в 50 раз — т.е., чтобы получить выигрыш один байт, надо сжимать 20,5 кб.
То есть если я сожму мегабайт на 1 байт это лично Вас убедит?
Давайте начнем хоть с чего-то. Тест, в котором ваш алгоритм, гарантированно сжимает любые (в том числе — патологические) 20.5кб байт-потока на один байт (и, естественно, гарантированно распаковывает его обратно) — неплохое начало.
ILIN-AIC Автор
04.04.2015 09:39Давайте начнем хоть с чего-то. Тест, в котором ваш алгоритм, гарантированно сжимает любые (в том числе — патологические) 20.5кб байт-потока на один байт (и, естественно, гарантированно распаковывает его обратно) — неплохое начало
Соблазнительно конечно, но хотелось бы взять фору увеличив размер такого блока до 100 килобайт. Причем надо сразу оговорить что данные в таком блоке должны быть с максимальной энтропией то есть заведомо не сжиматься никакими из уже существующих способов данных.
Что касается служебной информации: если убрать данные о количестве циклов и о их параметрах, поскольку цикл будет только один, то по предварительным прикидкам необходимо будет как минимум указать количество найденных АКС и количество оставшихся элементов кода.
Для 167936 бит как вы предлагаете это числа порядка (14919 и 100521, 14842 и 100945, 14709 и 100742 — проверено на 3 архивах). Можно записывать конечно только + — отклонения от средних значений. Это по грубым прикидкам минимум 8 бит для первого числа и 9 бит для второго числа. Причем это в среднем, а поскольку данные у нас будут совершенно случайными эти значения могут прыгать и выходить за пределы их матожиданий. Таким образом получаем еще как минимум 17 бит служебных данных…
Итого: (17+8)/0.00005
=500000 бит = 62500 байт = 61.03515625 Килобайт
При этом опять-таки для этого размера блока увеличивается размер служебной информации. При этом опять-таки для этого размера блока увеличивается размер служебной информации — около 20 бит.
Итак считаем: 100 килобайт
819200 бит * 0.00005 = 40.96 бит сокращения (Цифры приблизительные поскольку параметры от файла к файла прыгают)
40.96 — 20 бит (служебной информации) = 20.96 бит
Итог: сокращение 100 килобайт на два байта.

lair
04.04.2015 10:26Соблазнительно конечно, но хотелось бы взять фору увеличив размер такого блока до 100 килобайт.
Да мне все равно, на самом деле, какого размера будет блок, если время работы теста будет разумным.
Причем надо сразу оговорить что данные в таком блоке должны быть с максимальной энтропией то есть заведомо не сжиматься никакими из уже существующих способов данных.
Во-первых, вы прекрасно знаете, что это требование невыполнимо. Во-вторых, чем оно обосновано? Почему ваш алгоритм не может сжимать данные, которые сжимаются другими программами?
(тут снова возникает слово «матобоснование»)
по предварительным прикидкам необходимо будет как минимум указать количество найденных АКС и количество оставшихся элементов кода.
Эээ, то есть работающего алгоритма у вас нет? Если «по предварительным прикидкам»?
Но, повторюсь, мне все равно. 100к — так 100к. Два байта выигрыша — так два байта выигрыша (хотя я не понимаю, как вы их гарантируете, учитывая, что вы не знаете размер метаданных, но не важно). Условия все те же: для случайного входного набора данных — гарантированное сжатие как минимум на два байта и гарантированная распаковка в такой же набор (причем естественно, алгоритм не должен содержать словаря таких наборов данных).
ILIN-AIC Автор
04.04.2015 11:27Во-первых, вы прекрасно знаете, что это требование невыполнимо.
Почему? Есть куча заархивированных файлов которые не поддаются дальнейшему сжатию. Или тот же бинарный белый шум которые не поддается сжатию.
Почему ваш алгоритм не может сжимать данные, которые сжимаются другими программами?
Вообще не проблема сжать любым архиватором тот файл который вы предоставите, а затем уже ужимать моим алгоритмом. Если предоставленные данные будут с низкой энтропией и будут сжиматься архиватором это приведет к существенному лучшему результату. Однако боюсь это вызовет кривотолки… Ведь такие файлы сжимаются и любыми другими программами сжатия.
Эээ, то есть работающего алгоритма у вас нет? Если «по предварительным прикидкам»?
То есть работающего алгоритма у нас есть! «По предварительным прикидкам» потому что алгоритм писался для многоцикличного сжатия, где эти служебные данные записываются общей отдельной строкой которая затем сжимается.
Сейчас идет работа по улучшению алгоритмов поэтому решение, какой будет объем данных в тестовом файле, еще не принято. Некоторые вообще требуют сжать в 2 раза фильмы на dvd…
lair
04.04.2015 13:01Почему? Есть куча заархивированных файлов которые не поддаются дальнейшему сжатию.
Потому что невозможно (точнее, вычислительно неоправданно) доказать, что конкретный массив не будет сжиматься никаким существующим алгоритмом.
То есть работающего алгоритма у нас есть!
Значит, вы должно точно знать размер накладных расходов.
Сейчас идет работа по улучшению алгоритмов поэтому решение, какой будет объем данных в тестовом файле, еще не принято.
Вообще-то, это не связано. Если вы утверждаете, что один проход гарантированно сжимает данные на какой-то процент, то, значит, можно построить тест, в котором это будет видно.
Надо сначала доказать общую работоспособность, а затем заниматься «улучшением».
ILIN-AIC Автор
04.04.2015 13:16Значит, вы должно точно знать размер накладных расходов.
Это как все равно что по размеру архива определить какой был точный размер сжатого файла до сжатия
Если вы утверждаете, что один проход гарантированно сжимает данные на какой-то процент, то, значит, можно построить тест, в котором это будет видно.
Безусловно
Надо сначала доказать общую работоспособность
Зачем? Чтобы те кто совсем недавно доказывал невозможность этого бросились писать форки? С математической точки зрения я все уже доказал. Приоритет зафиксировал.
Кроме того эту особенность хаоса можно использовать не только для сжатия данных. Предоставляю простор для полета вашей мысли…
lair
04.04.2015 13:19Это как все равно что по размеру архива определить какой был точный размер сжатого файла до сжатия
Вообще-то — нет. Это как по настройкам сжатия знать размер метаданных.
С математической точки зрения я все уже доказал.
Приведите это доказательство.
ILIN-AIC Автор
04.04.2015 13:29Приведите это доказательство.
Кстати да. Можно закинуть еще в одной статье…

0serg
04.04.2015 21:53Сжать rar-архив с какими-то неслучайными данными и сжать случайный поток данных — это две принципиально разные задачи. RAR-архив не случайных данных сам по себе не случаен. Точно так же не случаен, к примеру, зашифрованный поток данных, хотя для стороннего наблюдателя в хороших шифрах он статистически неотличим от случайного. Не случайны и данные любого псевдослучайного генератора.
Поэтому задача «сжать RAR-архив» теоретически решаема. Не любая битовая последовательность является RAR-архивом и на этом можно сыграть. Но у этого процесса существует предел сжатия и колмогоровская сложность, собственно, является одним из наиболее удачных способов этот предел описать. Задача же «сжать случайные данные» — не решаема.

saluev
04.04.2015 02:04Я, честно говоря, вообще удивлён тому, что вы пришли без программы. Программа — она ведь решила бы все проблемы задолго до их появления (либо убедила бы нас, либо разубедила вас).

uvelichitel
03.04.2015 17:25Не совсем когерентно статье, но мне кажется что в современном распределенном мире репликация и шардинг данных стали асимптотатически значимей сжатия. Из этих пластинок до Плутона сколько уникальных?
horlon
03.04.2015 18:47-2Весьма интересная идея. Я и сам этим страдал. Заново переоткрыл и алгоритм Хаффмана, и Шеннона-Фано и много еще каких… Все-же, думаю бесконечное сжатие возможно (основываясь на том, что сжатые данные, это меньше, чем все возможные варианты). Меня удивляет схожесть Вашего мышления, и даже то, что, на днях (в этот понедельник) мне в голову пришла одна идейка (на намного проще Вашей, работает ли — не знаю, пока что не знаю), а тут Ваша статья на ту же тему. Моему удивлению нет предела…
Вычислительное время и мощьности на описанный Вами алгоритм, наверное, коллосальные… Такая задача, если и нерешима, то довольно хорошо развивает мышление — проверено…
Искренне желаю удачи.
ILIN-AIC Автор
03.04.2015 22:09Видимо идеи носятся в воздухе…
Насчет вычислительного времени — да с этим пока есть некоторые проблемы, думаю распараллеливание задачи должно помочь. Насчет вычислительных мощностей — ну будет на первых порах сжимать данные в фоновом режиме, пока не сделают специальный микропроцессор как под майнинг bitcoin. И вообще это только начало, есть пара идей как улучшить алгоритм.
grossws
04.04.2015 03:43+4Видимо идеи носятся в воздухе…
Да, в весенне-осенний период это всегда так.

Ivan_83
03.04.2015 18:53Пользуйся на здоровье: www.netlab.linkpc.net/download/software/SDK/core/include/math_bn.h
:)
Если сильно приспичит — в принципе могу переписать чтобы использовать вместо стёка динамически выделяемую память.
Есть ещё mpr и ещё пара либ в линухах, думаю и под венду легко портировать можно, если ещё не сделали.
ILIN-AIC Автор
03.04.2015 22:16-2Так это что же мне еще Си придется учить? Нет! Только basic только хардкор!

Sayonji
03.04.2015 20:00Честно признаю, текст не осилил. Если кто-то дочитал, можете пожалуйста вкратце пересказать идею автора? Вот так я бы вопрос поставил: строки какого вида его алгоритм будет увеличивать?

ILIN-AIC Автор
03.04.2015 22:40Если излагать кратко: автор проводил исследования хаотически расположенных данных, у которых мера хаоса (энтропия) максимальна. В этом хаосе автор нашел некоторые структуры данных которые более упорядочены (менее хаотичны) чем другие. Вместо того чтобы писать статьи в научные журналы и получать нобелевку, автор решил использовать открытие в корыстных для человечества целях: писать программы которые могут сжимать данные ( видео музыку книги картинки) в разы лучше, чем те что уже есть сейчас. Тем самым автор хочет на порядки увеличить скорость интернета, увеличить электронные устройства памяти практически до бесконечности и сделать информацию максимально доступной в любом уголке мира. Как всегда человечество (во всяком случае — наиболее просвещенная его часть русскоязычного сегмента) ответило в основном глухим недовольством на вероломные попытки подорвать стабильность и нарушить привычный ход вещей.
По второму вопросу
У автора коварный план — сокращать любые строки, увеличивать он собирается только файлы архивированные собственным архиватором. Этакое электронное monsanto :)
Sayonji
03.04.2015 23:18Ну тогда всё в порядке. Просто я бегло просмотрел комментарии, и возникло ощущение, что автор будто бы хочет вообще чуть ли не все строки сжимать. Т. е. будто бы матожидаение длины случайно выбранной строки из строк не длиннее N после архивации должно оказаться меньше N.

ILIN-AIC Автор
03.04.2015 23:38Так автор как раз и хочет все строки сжимать. У вас правильно возникает ощущение. Только во первых он перед этим хочет сжимать эти строки обычным способом. А кроме того при этом после сжатия обычным способом у автора минимальный размер сжимаемых данных мегабайт.
То есть например 10 гигабайт сжатых архивов ужимается до 10 мегабайт относительно без проблем, потом постепенно происходит резкое ухудшение параметров сжатия.
Sayonji
04.04.2015 01:55+1увеличивать он собирается только файлы архивированные собственным архиватором
Вы говорите «строки, не являющиеся уже результатом применения данного алгоритма», а затем говорите «все строки». Всё-таки надо определиться. Поскольку второе невозможно, а первое очень даже стандартно, не советую вам употреблять слово «все» в данном случае, а то вас и дальше будут не понимать.

Throwable
03.04.2015 22:02Вопрос на триллион: как удостовериться, что достигнутый «предел энтропии» таковым является? Пример для размышления: возьмем хорошую хеш функцию и нагенерируем при помози него увесистый блок псевдослучайных чисел. Архиватор скажет нам, что энтропия этого блока максимальна и что тут нефиг сжимать. Однако мы-то с вами знаем, чтобы воспроизвести весь этот блок необходима всего лишь записать функцию.
Или например так: возьмем текстовый файл. Архиватор сожмет его примерно до 30%. Теперь зашифруем его каким-нибудь алгоритмом сжатия. Теперь архиватор говорит, что тут опять нефиг сжимать и энтропия максимальна. Но мы-то с вами опять в теме…
Теперь абстрагируемся от деталей и предположим, что для каждой последовательности данных есть функция, ее кодирующая. Вопрос в том, как найти оптимальную функцию, кодирующую блок данных. Где-то на хабре предлагалось использовать число Pi, утверждая, что в нем содержится любая последовательность чисел (хотя и не доказано). Мы можем архивировать блок, просто указывая смещение в последовательности Pi ;)
Если серьезно, то подвох в том, что при подобном подходе либо подбор функции, либо само вычисление блока данных потребует бесконечных вычислительные ресурсов.
ILIN-AIC Автор
03.04.2015 23:02Насчет хаотических данных мы теперь с вами в теме…
В данный момент проблема как раз не с вычислительными ресурсами, а элементарно с вычислительным временем из-за неспособности задействовать эти самые ресурсы в параллельном режиме

tolika
04.04.2015 00:13-2Конечно, пример автора с его хитрыми подстановками не очень нагляден и больше напоминает манипуляции наперстночника («кручу, верчу — обмануть хочу»).
Но идеи в ходе обсуждения все же всплыли очень глубокие — жаль только, что они стали как-то забалтываться…
Насчет того, для архивации ВСЕХ N-битных сообщений потребуется столько же N-битных архивов спору нет — это элементарно.
Но суть-то (предположение) в том, что в реальных (большинстве имеющихся) сообщений (последовательностей) имеются скрытые закономерности («избыточность кода»). При обнаружении которых архив можно представить в укороченном виде. Т.е. формально он может и будет иметь длину N бит, но последние М этих бит будут = 0
(кстати, интуитивно эта идея воспринимается в понятии «круглых чисел», а технически — в самом процессе округления (хотя это уже и сжатие с потерями...)).
Таким образом задача архивирования сводится к оптимальному перераспределению соответствий исходных последовательностей и их образов (архивов) — так же как, например, в азбуке Морзе более частотным буквам соответствуют более короткие комбинации.
Вот только пытаться навязать свой алгоритм подобной оптимизации — как-то не совсем научно… В принципе, алгоритм нахождения подобных «флуктуаций хаоса» должен быть универсальным — скорее всего такой алгоритм должен не бросаться тупо архивировать данные на основе какой-то жесткой схемы, а подобрать оптимальный алгоритм такой архивации в зависимости от данных (т.е. выйти на другой уровень обработки информации).
Реализовать подобную программу лучше всего, наверное, на уровне нейронных сетей. Но это уже дело техники (кстати обучать ее особо не придется — задать миллион типичных исходных файлов и пусть тренируется — глядишь и выявит какие-нибудь вселенские закономерности :-).

Hoshi
04.04.2015 04:03+2Попробую обьяснить невозможность создания такого архиватора простыми словами:
Предположим имеется файл размером N бит, тогда возможных вариантов файлов такого размера — 2N штук.
Сжав этот файл архиватором мы хотим получить архив размером M бит где M < N (размер архива должен быть меньше исходника).
И тут возникает проблема — возможных вариантов архивных файлов у нас 2M что меньше чем количество возможных исходных файлов 2N следовательно не всем исходным файлам мы можем сопоставить файл архива.
Из этого можно сделать вывод что наш сжимающий архиватор сжимает не все возможные файлы, а только их часть. Остальные-же файлы проще всего не сжимать вовсе.
А так как в реальной жизни содержимое файлов распределено неравномерно то можно сказать что написанние архиватора есть выбор алгоритма сопоставления множества M с множеством N таким образом чтобы во множество M попадало как можно больше реально-существующих(полезных) наборов данных.
ЗЫ: Под архивом подразумевается любой набор данных будь-то хитрый алгоритм или набор смещений+словарь либо ещё что…
a5b
04.04.2015 12:08С 2002 года открыт для участия конкурс по сжатию случайных данных от Mark Nelson с денежным призом в случае успеха:
* 2002: groups.google.com/forum/#!msg/comp.compression/BrES5syH_Rk/555gYFcmT4EJ
* 2006: marknelson.us/2006/06/20/million-digit-challenge/
* 2012: www.drdobbs.com/architecture-and-design/the-enduring-challenge-of-compressing-ra/240049914 (http://marknelson.us/2012/10/09/the-random-compression-challenge-turns-ten/)
Нужно сжать файл marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin с 415241 байт до 415240 байта, однако в объём сжатых данных должен быть включён код распаковщика.
reduce the size of roughly half a megabyte of random data – by as little as one byte – and be the first to actually have a legitimate claim to this accomplishment.
… The size of the decompressor and data file added together must be less than 415,241 bytes.
С момента объявления конкурс так и не выигран. При этом автор указывает 2 варианта:
* «Challenge Version 1 – A Kolmogorov Compressor… find the shortest program possible that will produce the million random digit file. In other words, demonstrate that its Kolmogorov complexity is less than its size.… The interesting part about this challenge is that it is only very likely impossible.»
* «Challenge Version 2 – A General Purpose Random Compressor… it is patently impossible: create a system to compress and then decompress any file of size 415,241 bytes. In other words, create a compressed file that is smaller than the input, then use only that compressed file to restore the original data.… there are no size limitations on Challenge 2. Your compressor and decompressor can be as large as you like. Because the programs have to be able to handle any input data, „
Если б не условие по учету размера распаковщика, то первую задачу успешно решает экспериментальный компрессор BARF от mattmahoney.net/dc/barf.html (автор нескольких вариантов ZPAQ). Он сжимает абсолютно любой файл, уменьшая размер данных файла на 1 байт. Кроме того, он успешно сжимает классический тестовый набор Calgary Corpus с 3.141 МБ до 14 байт (!). Размер распаковщика — около 1 МБ.
The BARF compressor will compress any nonempty file by at least one byte. Thus, by compressing already compressed files over and over again, it is possible to eventually reduce any file to 0 bytes.
BARF has been tested on the Calgary corpus, a well known benchmark. In just one pass, it achieves the best known result of any compressor, compressing all 14 files to 1 byte each. Run time is under 1 second on a 750 MHz PC.
Принцип работы — распознавание файлов из состава Calgary, либо удаление одного байта из содержимого файла и его запись в виде дополнительного расширения в имени файла (глубина рекурсивности сжатия может быть ограничена устаревшими файловыми системами):
if the input is the i'th (1-14) file of the Calgary corpus
then encode it as a 1 byte file with byte value i-1
…
Method n is as follows:
if the first byte is n-2 then remove it
Method n (2-257) is indicated by an extension of the form .x[0-9][a-z] as a base 26 encoding of n-2.

ILIN-AIC Автор
04.04.2015 12:40-1Нужно сжать файл marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin с 415241 байт до 415240 байта, однако в объём сжатых данных должен быть включён код распаковщика.
Ну насчет требований по включению в этот объем распаковщика это понятно. Страхуются от мошенников. Правда я прикинул что в таких случаях распаковщик нужно писать примерно на ассемблере.
Принцип работы — распознавание файлов из состава Calgary, либо удаление одного байта из содержимого файла и его запись в виде дополнительного расширения в имени файла
Короче мошенничество.horlon
10.04.2015 20:52-3Можно написать на интерпретируемом языке Python, PHP (не читал правила, не знаю можно ли).
А если серьезно. Кто-то всерьез считает, что архиватор такого уровня стоит 100$? Или я что-то не понял? Это же смешно! Не находите? Это чистое воровство!
P.S. Если ты изобрел что-то и отдаешь его бесплатно. Всегда найдется кто-то кто на этом заработает и даже не вспомнит о тебе…

SerJook
04.04.2015 13:46Я тоже когда-то думал, что придумал алгоритм сжатия, который принесет мне мировую славу, но оказалось, что я всего лишь придумал Код Хаффмана :(

dtestyk
04.04.2015 16:03допустим, существует алгоритм, сжимающий произвольные данные, применив его рекурсивно много раз получим 1 бит, но информация никуда не делась, теперь она закодирована в количестве рекурсий

fshp
04.04.2015 16:44+6Закон Попова-Бабушкина — каждые 24 месяца на свет рождается очередной Попов-Бабушкин.

ILIN-AIC Автор
04.04.2015 17:54-3Вы еще Петрика забыли ;)
ru.wikipedia.org/wiki/%D0%9F%D0%B5%D1%82%D1%80%D0%B8%D0%BA,_%D0%92%D0%B8%D0%BA%D1%82%D0%BE%D1%80_%D0%98%D0%B2%D0%B0%D0%BD%D0%BE%D0%B2%D0%B8%D1%87

tolika
05.04.2015 03:13-3Публичный словарь для сжатия.
То есть в отдельно взятом онлайн хранилище, хранятся проиндексированные длинные последовательности различных данных.
Архиватор сжимает файл, используя этот словарь.
Может этот «публичный словарь» и есть азбука, счет и прочие «навыки», которые позволяют получить доступ (понять) к залежам информации, которая для необразованного представляет сплошной хаос?.. ("… я ходила на концерт / слушала бетховена / только время потеряла / ну блин и фиговина...") — кстати, в совецкие времена перед показом по телевизору классической музыки обычно предварительно выступала умная тетка и долго и нудно объясняла — про что в этой «сифмонии» рассказывается… — эдакий встроенный разархиватор для тех кому архиватор в школе не закачали…
А более масштабно под таким словарем можно понимать все собранные и записанные человечеством сведения — а уже через призму этого словаря люди воспринимают («познают») себя, окружающих и природу (многие ли сейчас способны на «непосредственное восприятие»?)
В этом случае азбуку и проч сведения, дающие доступ к этому словарю, можно рассматривать как некий базовый словарь или BIOS или интерфейс…
Это я все к тому — может при изобретении архиватора использовать уже сформировавшиеся тысячелетиями методы, а не начинать с нуля?
Самолет ведь тоже разрабатывали, глядя на птиц… (кстати, они явно тяжелее воздуха...).
PS
Извиняюсь за сумбурность, но пытаюсь говорить на «уровне идей» — если всё это сформулировать научно, получится слишком много букв и мат. символов.

ILIN-AIC Автор
05.04.2015 13:26Внимание, уважаемое сообщество!
В ходе тестовых испытаний алгоритма сжатия, в связи вот с этим комментарием habrahabr.ru/post/254809/#comment_8361011, были проведены тесты по сжатию файла AMillionRandomDigits.bin, взятым вот отсюда: marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin
В связи с полученными результатами у меня большая просьба к как можно большему числу людей прямо сейчас скачать этот файл и сохранить у себя (он занимает всего 415241 байт). Можно его сохранить также в виде различных архивов, что, кстати, подтвердит его не сжимаемость существующими программами сжатия.
Также большая просьба сохранить и заскринить вот эту страничку: marknelson.us/2006/06/20/million-digit-challenge/
P.S. Сжатый файл и распаковщик к нему постараюсь выложить сегодня.

lair
05.04.2015 19:35+1Колмогоров в вышеуказанной статье математически доказал обратное в рамках инструментария теории алгоритмов. Другими словами для любых данных, некоторой достаточно большой длины, всегда найдется программа точно воспроизводящая эти данные, запись которой будет меньше, чем длинна этих данных.
Я прочитал статью и не нашел там этого утверждения. Можете привести точную цитату?
ILIN-AIC Автор
06.04.2015 08:26Сразу задам встречный вопрос: вышеуказанный файл (marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin) удовлетворяет вашим критериям случайности данных?
““““““““““
Я прочитал статью и не нашел там этого утверждения. Можете привести точную цитату?
””””””””””
А как в таком случае Вы понимаете основную теорему в третьем параграфе?
“Основная теорема. Существует такая частично рекурсивная функция A(p,x), что для любой другой частично рекурсивной функции ?(p,x) выполнено неравенство
KA(y j x) K'(y j x) +C' ”
2 столбец 5 стр.:
«то
A((n; p); x) = y;
l(n; p) l(p) +Cn:»
"«IA(x: y) не
меньше некоторой отрицательной константы C,
зависящей лишь от условностей избранного мето-
да программирования. Как уже говорилось, вся
теория рассчитана на применение к большим ко-
личествам информации, по сравнению с которым
jCj будет пренебрежимо мал.»
С учетом замечаний в четвертом параграфе:
«Введя надлежащие определения,
можно доказать точно формулируемые матема-
тические предложения, которые законно интер-
претировать как указание на существование та-
ких случаев, когда объект, допускающий очень
простую программу, т. е. обладающий очень ма-
лой сложностью K(x), может быть восстановлен
по коротким программам лишь в результате вы-
числений совершенно нереальной длительности.»
lair
06.04.2015 08:47Сразу задам встречный вопрос: вышеуказанный файл (marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin) удовлетворяет вашим критериям случайности данных?
Что за мои «критерии случайности данных»? Если вы о тесте, который я вам выше предлагал — то нет, не удовлетворяет, поскольку в этом тесте программе должны подаваться на вход каждый раз разные данные.
А как в таком случае Вы понимаете основную теорему в третьем параграфе?
Таким, что минимальная вычислительная сложность некоей информации не превышает символьного объема этой информации плюс некая константа, не зависящая от символьного объема.
ILIN-AIC Автор
06.04.2015 09:09"«Что за мои «критерии случайности данных»?»"
Ну как выяснилось из предыдущего обсуждения каждый понимает под этим нечто свое. Хотелось бы узнать ваши критерии.
"«Таким, что минимальная вычислительная сложность некоей информации не превышает символьного объема этой информации плюс некая константа, не зависящая от символьного объема. „“
Латинская l в статье означает длинну
lair
06.04.2015 11:05Латинская l в статье означает длинну
Это никак не меняет (и не противоречит) моего утверждения.

0serg
06.04.2015 12:38+1А как в таком случае Вы понимаете основную теорему в третьем параграфе?
Основная теорема в третьем параграфе говорит что существует такой язык программирования A что колмогоровская сложность y относительно x определенная в рамках этого языка превышает колмогоровскую сложность y относительно x в рамках любого другого языка phi не более чем на некоторую константу зависящую от языка phi.
Проще говоря эта теорема говорит о том что в рамках теории колмогоровской сложности существует асимптотически оптимальный метод программирования и выбор любого другого языка программирования не позволяет получить существенного выигрыша относительного этого метода какие бы x и y не использовались. Это критично для определения, т.к. иначе пришлось бы рассматривать колмогоровскую сложность не саму по себе, а в привязке к конкретным языкам программирования.
Вот и все. Каким образом Вы прочитали эту теорему иначе?
Ваше определение «суперсжатия» в рамках цитируемой работы должно звучать примерно так: существует такой phi что для любого достаточно большого x (исходных данных) найдется такое y (сжатые данные) что
K_phi(y|x) < l(x)-l(y) (размер программы разархивирования меньше чем выигрыш в сжатии)
Но естественно ничего подобного у Колмогорова нет.
ILIN-AIC Автор
06.04.2015 13:03-1"«не позволяет получить существенного выигрыша относительного этого метода»"
Как у меня о _существенном_ выигрыше речи нет — в лучшем случае 0.00005 за один цикл
lair
06.04.2015 13:12У вас идет речь о не-константном выигрыше, поэтому это уже не укладывается в формулу выше.

0serg
06.04.2015 14:45+1Так мои претензии и не к константе :)
Вы абсолютно неверно интерпретируете теорему, я с трудом представляю даже откуда вообще взялась Ваша интерпретация.
ILIN-AIC Автор
06.04.2015 14:52Много лет назад читал труды Колмогорова по теории алгоритмов. Если как вы считаете Колмогоров ничего такого не писал то это еще лучше.
Предлагаю сосредоточиться на моем алгоритме.
lair
06.04.2015 15:02+1Вы, главное, из поста уберите фразу, что Колмогоров утверждает возможность вашего алгоритма. Чтобы людей в заблуждение не вводить.

0serg
06.04.2015 15:19+2Какой смысл сосредотачиваться на разборе ошибок в конструкции «вечного двигателя»? Вы же даже если Вам указать на ошибку (что требует достаточно большого объема работы) начнете говорить что её можно легко исправить. Практика, увы, проверенная временем. Доказательство того почему «бесконечного сжатия» не бывает я Вам уже привел и это доказательство значительно проще чем Ваш алгоритм. Хотите чтобы к Вашему алгоритму присмотрелись серьезнее несмотря на то что по всем признакам это пустышка? Тогда продемонстрируйте с его помощью хоть какой-то интересный результат. В комментах Вы хвалитесь что сумели сжать AMillionRandomDigits.bin — вперед, продемонстрируйте хотя бы сжатие этого файла.

ILIN-AIC Автор
07.04.2015 11:12Движемся в эту сторону…
a5b
07.04.2015 11:27Не забывайте, по условиям marknelson.us/2006/06/20/million-digit-challenge/ недостаточно просто сжать файл, еще требуется чтобы суммарный размер декомпрессора и сжатого файла был меньше чем размер миллиона случайных цифр:
«The challenge is to create a decompressor + data file that when executed together create a copy of this file.
The size of the decompressor and data file added together must be less than 415,241 bytes.»
ILIN-AIC Автор
07.04.2015 11:38Да я помню. Все дело в повторном многократном циклическом сжатии. Причем по моим прикидкам программа должна быть примерно на ассемблере для того чтобы занимать как можно меньше места.

0serg
07.04.2015 12:48Начните с создания сжатых файлов, без учета программы сжатия.
Ставлю 10 к 1 что Вам не удастся этого сделать.
Условие о включении кода программы в архив в основном служит для отсечки недобросовестных решений которые будут просто включать (полностью или фрагментами) в себя кусок сжимаемого файла.

lair
05.04.2015 23:59+3Другими словами для любых данных, некоторой достаточно большой длины, всегда найдется программа точно воспроизводящая эти данные, запись которой будет меньше, чем длинна этих данных.
Извините, но нет. Открываем википедию, статья «Колмогоровская сложность», и читаем: «There exist strings of arbitrarily large Kolmogorov complexity. Formally: for each n ? ?, there is a string s with K(s) ? n.» Доказательство там же.
Или в русской википедии: «Согласно определению колмогоровской случайности (тж. алгоритмической случайности) строка называется случайной тогда и только тогда, когда она короче любой компьютерной программы, способной её воспроизвести. [...] С помощью принципа Дирихле легко показать, что для любой универсальной машины существуют алгоритмически случайные строки любой длины, однако свойство строки быть алгоритмически случайной зависит от выбора универсальной машины.»
Таким образом, ваши отсылки к алгоритмической сложности Колмогорова можно считать несостоятельными.
ILIN-AIC Автор
06.04.2015 08:57"«Извините, но нет. Открываем википедию...»"
:) Извините, но да. Читаем внимательно первоисточник (compression.ru/download/articles/ti/kolmogorov_1965_three_way_pdf.rar). В предыдущем комментарии я указал где именно.
Ваши цитаты из википедии, содержащие записанные кем-то чьи-то мысли относительно первоисточника, никак не могут подменять самого первоисточника.
"«Таким образом, ваши отсылки к алгоритмической сложности Колмогорова можно считать несостоятельными»"
Скорее, таким образом, ваши отсылки к цитатам из википедии можно считать несостоятельными.
Кстати хотелось бы поближе обсуждению самой обсуждаемой статьи и в частности утверждению, что в случайных данных можно вычленить последовательности с логарифмом вероятности их появления отклоняющимся от длин этих последовательностей.
lair
06.04.2015 09:03Вас, видимо, не смущает тот факт, что первоисточник обсуждает способы измерения количества информации, а не ее сжатия. Повторюсь, нигде в первоисточнике не написано то, что вы ему приписываете.
А про обсуждаемую статью уже все сказано: просто покажите алгоритм или дайте работающий тест.
ILIN-AIC Автор
06.04.2015 09:16"«Вас, видимо, не смущает тот факт, что первоисточник обсуждает способы измерения количества информации, а не ее сжатия. Повторюсь, нигде в первоисточнике не написано то, что вы ему приписываете.»"
Все дело в том, что первоисточник обсуждает способы измерения количества информации через ее запись или отображение. Более короткое отображение информации именуется сжатием.
"«просто покажите алгоритм»"
Вроде бы уже показал. Что непонятно?
chersanya
06.04.2015 09:23Вы вчера вроде как собирались выложить работающую программу :)

ILIN-AIC Автор
06.04.2015 09:28Программу-распаковщик я выложу. Как я уже говорил, необходима более длинная арифметика арифметического кодирования кода расположения АКС. Хотите помочь? :)

lair
06.04.2015 09:31Не нужна она (арифметика). В демонстрационных целях можно вообще на символах все сделать.

ILIN-AIC Автор
06.04.2015 09:36Хорошо покажем на символах. Какие файлы (помимо AMillionRandomDigits.bin) будем сжимать?
PS И кстати на Хабре есть куда файлы положить?
lair
06.04.2015 09:43Я же говорил уже: берете криптографический генератор случайных чисел, генерите из него каждый раз новую последовательность, на ней тестируете. Отдельными тестами — Нельсоновский файл и корпус Кентербери.

ILIN-AIC Автор
06.04.2015 09:49"«берете криптографический генератор случайных чисел, генерите из него каждый раз новую последовательность»"
Так откуда Вы будете знать что этот файл взят именно оттуда. Меня ж тут в Поповы-Бабушкины записали… Так сказать презумпция виновности :)
AMillionRandomDigits.bin Под категорию случайных данных пропадает? Вроде как он тестировался уже с 2002 года…
Также можете сами дать ссылки на какие-либо случайные последовательности.
lair
06.04.2015 09:53А мне не надо это знать. Я просто возьму новую последовательность и прогоню ее через аналогичный тест. Если целевые характеристики не будут соблюдены — тест провален. А раз ваш алгоритм детерминирован, это поведение будет повторяться у любого, кто будет повторять тест на таких входных данных.

chersanya
06.04.2015 10:05Выложите хоть что-нибудь! Не важно, насколько быстро это будет работать, главное чтобы каждый мог проверить: взять любой файл, сжать его, потом разжать. Исходники, кстати, тоже не обязательно :)

ILIN-AIC Автор
06.04.2015 10:21Так исходники уже и так по сути уже выложены (в статье ;)

chersanya
06.04.2015 10:24В статье описание алгоритма в очень свободной форме. Чем спорить, выложили бы программу — эти вопросы сразу бы разрешились.

ILIN-AIC Автор
06.04.2015 10:36Сейчас попробую скомпилировать то что есть. Предчувствую комментарии что-то типа:
'''Вы взрослый человек, Гедеван Александрович. Вы проучились один семестр и исчезли на годы! Объявились! _С каким-то камешком, с каким-то обломком кавказской керамики и колокольчиком от донки!_ А претендуете на… Ну, и к тому же, если вы способны музицировать, то почему вы не принимали участия в нашей курсовой самодеятельности? Вы извините меня, Скрипач, но это элементарное ку!''' © Кин-дза-дза
lair
06.04.2015 17:50И что же, за пять часов компиляция так и не завершилась? Или результат не работает?
a5b
07.04.2015 11:31Еще раз, mark nelson указывает 2 варианта конкурса:
* «Challenge Version 1 – A Kolmogorov Compressor… million random digit file.» — это вариант с тем файлом. В зачет идет размер декомпрессора И сжатого файла в сумме.
А тут от вас хотят второй вариант — в котором компрессор и декомпрессор в зачет не идут, но надо сжать не один файл с случайными данными, а ЛЮБОЙ (каждый возможный). Тестировать это можно так: генерируем 415241 байт случайных данных, сжимаем, измеряем — если получилось меньше — пробуем следующий случайный вариант, получилось больше — засчитываем поражение в конкурсе.
* «Challenge Version 2 – A General Purpose Random Compressor… it is patently impossible: create a system to compress and then decompress any file of size 415,241 bytes. In other words, create a compressed file that is smaller than the input, then use only that compressed file to restore the original data.… there are no size limitations on Challenge 2. Your compressor and decompressor can be as large as you like. Because the programs have to be able to handle any input data, „

lair
06.04.2015 11:03Все дело в том, что первоисточник обсуждает способы измерения количества информации через ее запись или отображение. Более короткое отображение информации именуется сжатием.
С этим никто не спорит. Но нигде в первоисточнике нет утверждения — на которое вы неоднократно ссылаетесь — что для любой информации возможно более короткое отображение.
Вроде бы уже показал. Что непонятно?
Непонятен сам алгоритм. Вы показываете некие — незавершенные! — принципы. Например, предположим, что вы изымаете из исходной последовательности все 101. Как вы храните указатели на места, откуда те изъяты?
ILIN-AIC Автор
06.04.2015 11:15В виде отдельного бинарного файла — где 1 — 101, а 0 — остальные знаки. Просто суть в том, что
1 не все 101 нужно указывать
2 не везде 101 может находиться
Эти две особенности сокращают длину такого файла количество единиц ( указание на акс) в нём
lair
06.04.2015 11:17Если у вас есть «особенности», значит, должен быть отдельный — формализованный — алгоритм записи и чтения с их учетом. И да, вы считали ожидание размера такого файла исходя из равновероятного потока?

ILIN-AIC Автор
06.04.2015 11:55''''Если у вас есть «особенности», значит, должен быть отдельный — формализованный — алгоритм записи и чтения с их учетом''''
Именно так и есть.
''''И да, вы считали ожидание размера такого файла исходя из равновероятного потока? '''
Да все делалось именно для случайных величин. Так например для того самого пресловутого тестового файла AMillionRandomDigits.bin длина бинарного файла 3321928 бит.
Длина кода расположения АКС для него 2286631 бит (292405 единиц и 1994226 нулей). Логарифм вероятности появления АКС — 2.96718368674378 при длине самого АКС три бита. Итого такой код сжимается по формуле Шеннона до 1261268.904 бит.
Затем АКС убираем. И записываем АКС в новом расположении с таким кодом, у которого логарифм вероятности появления АКС — равен длине АКС 3 бита. Это 284890 АКС среди 1994226 остальных знаков — код имеет энтропию по формуле Шеннона 1238846.109 бит. (Причем этот код мы берем не произвольно, а из определенной части сжимаемых данных ( например код расположения одного из знаков восьмеричного кода имеет примерно такую же вероятность)).
Итого сократили -7515 АКС по 3 бита = -22545 бит.
Коды расположения уменьшились1238846.109 — 1261268.904 = -22422.79479.
Разница составляет -123.9194967 бит общего уменьшения кода.
lair
06.04.2015 11:58Именно так и есть.
Нет, так «не есть». Формального описания алгоритма в вашем посте нет.
Да все делалось именно для случайных величин. Так например для того самого пресловутого тестового файла AMillionRandomDigits.bin длина бинарного файла 3321928 бит. Длина кода расположения АКС для него 2286631 бит (292405 единиц и 1994226 нулей).
Это вы приводите данные для конкретного потока. А я прошу ожидание для любого потока исходя из того, что 0 и 1 внутри него равновероятны.
А для «пресловутого тестового файла» должны быть не вероятностные значения, а конкретные после прохода вашего алгоритма.
ILIN-AIC Автор
06.04.2015 12:07"«я прошу ожидание для любого потока исходя из того, что 0 и 1 внутри него равновероятны.»"
вероятность 0.12783
«для «пресловутого тестового файла» должны быть не вероятностные значения, а конкретные после прохода вашего алгоритма. „
Выше и были приведены конкретные значения
lair
06.04.2015 12:12вероятность 0.12783
Я просил ожидание размера файла позиций.
Выше и были приведены конкретные значения
Т.е. вы можете назвать конкретные размеры результирующего файла после сжатия и файла метаданных?
ILIN-AIC Автор
06.04.2015 12:26Математическое ожидание длины кода расположения АКС «101» 0.68831 от длины первоначального кода
В сжатом виде 0.379586026 от длины первоначального кода
lair
06.04.2015 12:35Расчет привести можете?

ILIN-AIC Автор
06.04.2015 12:57-1По сути вы предлагаете мне привести математическое доказательство данных параметров. Это работа для отдельной (причем научной) статьи.
Меня в данный момент интересует практическое применение данных параметров. Поэтому я занимаюсь программой кодирования, которую каждый сможет запустить и проверить результаты на каких угодно файлах.
В принципе те же самые результаты можно получить эмпирически взяв бинарный код случайных данных пусть даже небольшого размера 10 000 знаков и в текстовом редакторе Word произвести все замены при помощи функции замена текста.
1) Замена 101 -> 2 (записываем N найденных)
2) удаляем 2
3) Опять замена 101 -> 2 (записываем M найденных)
4) Количество АКС расположение которых нужно указывать X=N-M
5) Замена 100 на 13
6) Опять удаляем 2
7) Смотрим количество оставшихся знаков Y
Код расположения вычисляется для Х АКС среди Y оставшихся знаков.
Вероятность встречаемости АКС = X: (X + Y)
Хотите произведите сами математическое обоснование и опубликуйте. Постараюсь по мере сил помочь
lair
06.04.2015 13:00По сути вы предлагаете мне привести математическое доказательство данных параметров.
Конечно. Ожидание нельзя получить иначе как математическим расчетом (ну то есть вру, можно — еще перебором).
Это работа для отдельной (причем научной) статьи.
Вообще-то, это сравнительно простой расчет. Другое дело, что вы его не проводили, судя по всему.
В принципе те же самые результаты можно получить эмпирически взяв бинарный код случайных данных пусть даже небольшого размера 10 000 знаков и в текстовом редакторе Word произвести все замены при помощи функции замена текста.
Вы правда не понимаете разницы между расчитанным ожиданием и результатом в конкретном примере?
ILIN-AIC Автор
06.04.2015 13:15""(ну то есть вру, можно — еще перебором""
Врать нехорошо ( шутка ;)
"«Вообще-то, это сравнительно простой расчет. Другое дело, что вы его не проводили, судя по всему.»"
Не проводил поскольку это мне не нужно. Мне хватило тестирования многочисленных данных. Меня интересуют практические аспекты.
Если как вы утверждаете это довольно простой расчет — проведите его я вам помогу. Заодно теоретически опровергните (как видимо вы полагаете) мои постулаты.
"«Вы правда не понимаете разницы между расчитанным ожиданием и результатом в конкретном примере? „“
Все я понимаю. Просто для моих целей хватает данных полученных эмпирическим путем.
Ссылка на вашу любимую википедию ru.wikipedia.org/wiki/%D0%AD%D0%BC%D0%BF%D0%B8%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C
Постскриптум. А на счет теоретических расчетов я говорю серьезно — посчитайте а я вам помогу
lair
06.04.2015 13:34Не проводил поскольку это мне не нужно.
QED. Непонятно только, зачем вы выше выдаете свои эмпирические результаты за ожидание.
Окей, следующий вопрос: ваш «отдельный бинарный файл» представляет собой битовую маску, указывающую на положения 101 в исходном файле, или список позиций?
ILIN-AIC Автор
06.04.2015 14:09«Непонятно только, зачем вы выше выдаете свои эмпирические результаты за ожидание»
Цитата с нашей любимой википедии:)
«Эмпири?ческая закономе?рность (от греч. ???????? — опыт)… — зависимость, основанная на экспериментальных данных и позволяющая получить приблизительный результат, в типичных ситуациях близкий к точному[1]. Такие закономерности легко запоминаются и дают возможность обходиться без сложных инструментальных измерений, чтобы вычислить некую величину. Подобные принципы используются в эвристике, широко распространённой в математике, психологии и информатике.
Закономерность обычно выражается в виде математической формулы, отражающей наблюдаемые результаты с достаточной точностью. Такая формула либо не имеет строгого теоретического вывода, либо является достаточно простым аналогом более сложного точного теоретического соотношения.»
ru.wikipedia.org/wiki/%D0%AD%D0%BC%D0%BF%D0%B8%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%B7%D0%B0%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C
«следующий вопрос: ваш «отдельный бинарный файл» представляет собой битовую маску, указывающую на положения 101 в исходном файле, или список позиций?»
представляет собой битовую маску, указывающую на положения 101 в исходном файле
lair
06.04.2015 14:30представляет собой битовую маску, указывающую на положения 101 в исходном файле
В таком случае без оптимизации его размер строго равен n, а с оптимизацией — n-2m, где n — размер входного файла, а m — количество вхождений 101. Никакого .6 и .3.
Если предположить, что исходный файл содержит ~1/8 вхождений 101 (что, если я не ошибаюсь, проистекает из его равновероятной структуры), то размер файла позиций будет составлять ~3/4n.
ILIN-AIC Автор
06.04.2015 14:47«В таком случае без оптимизации его размер строго равен n, а с оптимизацией — n-2m, где n — размер входного файла, а m — количество вхождений 101. Никакого .6 и .3.»
1) Исключены позиции в которых 2 после замены 101 находиться не может (10*0) 1020 -> «101»010 -> 2010
2) Исключены из кода расположения указания на 101 которые должны обязательно находиться в определенных местах после того как мы убрали 101 ( во вновь получившихся 101 обязательно должна было быть хотя бы одно 101: 110101 -> 101 иначе мы бы его автоматически убрали)
Я просто выложу программу которая генерирует из двух файлов: файла кода расположения и файла состоящего из знаков оставшихся после изъятия 101 первоначальный файл.
lair
06.04.2015 14:50И какова вероятность таких «исключений»? И, как следствие, ожидание вашего результата?
Ну и да, вы эту программу обещаете выложить уже несколько дней, а воз и ныне там.
ILIN-AIC Автор
06.04.2015 14:58"«И какова вероятность таких «исключений»? И, как следствие, ожидание вашего результата?»"
Эмпирически полученные цифры я вам указал.
""«Ну и да, вы эту программу обещаете выложить уже несколько дней, а воз и ныне там. „“
Не „несколько дней“, а вчера пообещал что возможно выложу. И ушел с головой в арифметическое кодирование, чтобы сжать код расположения АКС…
Все пойду заниматься программой…
lair
06.04.2015 15:01+1Эмпирически полученные цифры я вам указал.
QED. Вы не знаете поведение вашего алгоритма ни в статистическом случае, ни в патологическом случае.

ILIN-AIC Автор
06.04.2015 12:02"«И записываем АКС в новом расположении с таким кодом, у которого логарифм вероятности появления АКС — равен длине АКС 3 бита.»"
Хочу заметить, что не обязательно новая вероятность появления АКС должна быть _точно_ равна этому параметру. Однако максимум функции сжатия достигается именно при равенстве логарифма вероятности появления АКС его длине.

ILIN-AIC Автор
06.04.2015 09:42«в соответствии с теоремой Геделя о неполноте формальных систем, нельзя доказать, что минимальная длина программы L(P) преобразования X в Y, составленная на каком-либо языке программирования, действительно является объективно минимальной» (Вяткин В.Б. ЗАДАЧА ОЦЕНКИ НЕГЭНТРОПИИ ОТРАЖЕНИЯ СИСТЕМНЫХ ОБЪЕКТОВ И ТРАДИЦИОННЫЕ ПОДХОДЫ К КОЛИЧЕСТВЕННОМУ ОПРЕДЕЛЕНИЮ ИНФОРМАЦИИ vbvvbv.narod.ru/problemnegentropy/algoritm/index.htm)
То есть теоретически всегда можно написать более короткую программу

ILIN-AIC Автор
07.04.2015 11:03-2Итак уважаемые сообщество выкладываю тестовые файлы вместе с декодером к ним, которые можно скачать по адресу: www.ilin.biz/files/AIunCoder01.zip
Краткий FAQ к тестовой программе AIunCoder01.exe
В. Что это?
О. zip-архив с папкой AIunCoder01 в которой находятся файлы AIunCoder01.exe, ai1-locat.txt, ai2-field.txt
В. Что это за файлы?
О. Это бинарные (двоичные) файлы, на которые мы разложили тестовый файл AMillionRandomDigits.bin. В частности ai1-locat.txt — это файл кода расположения АКС (101), а файл ai2-field.txt — это файл кода который остался после изъятия этих АКС. AIunCoder01.exe – это декодер, который восстанавливает этих кодов исходный файл AMillionRandomDigits.bin.
В. Что мне с ними делать?
О. Скопировать все 3 файла на диск С:\ (в корневую директорию) и запустить декодер AIunCoder01.exe (на часик или больше в зависимости от мощности компьютера ;) после чего на диске С:\ раскодируется AMillionRandomDigits.bin
В. Что это за файл AMillionRandomDigits.bin?
О. «Широко известный в узких кругах» файл AMillionRandomDigits.bin выложен Марком Нельсоном на своей страничке (marknelson.us/attachments/million-digit-challenge/AMillionRandomDigits.bin) в 2002 году как пример нагромождения случайных данных, которые невозможно сжать существующими способами сжатия данных. И действительно с 2002 года его еще до сих пор никто не сжал. Подробно обо всех попытках получить денежный приз можно почитать на страничке Нельсона: marknelson.us/2006/06/20/million-digit-challenge/
В. А вы что его сжали?
О. Пока нет, но близок к этому. Выложенные мной файлы демонстрируют работоспособность алгоритма разложения исходных файлов на части, которые можно затем сжать и самое главное возможность, затем из этих частей восстановить первоначальный файл.
В. Еще чем-то примечательны выложенные вами файлы?
О. Примечательно то, что в файле кода расположения ai1-locat.txt количество указаний на АКС (количество единичек, которые находятся среди остальных знаков, представленных нулями) значительно меньше, чем самих изъятых АКС. И сама длина кода расположения существенно короче первоначальной длины двоичного представления исходного файла AMillionRandomDigits.bin.
В. И о чем нам это должно говорить?
О. А том, что благодаря найденным закономерностям в случайных данных, в которых по самому определению эти закономерности должны отсутствовать мы можем несколько сократить код представления этих данных, частности больше чем позволяет их энтропия, перепрыгнув через «энтропийный барьер».
В. Почему же тогда в таком случае вы не сжали сам файл AMillionRandomDigits.bin?
О. Для этого необходимо произвести арифметическое кодирование файла кода расположения ai1-locat.txt как можно с меньшими потерями как можно ближе приблизившись к теоретическому пределу сжатия.
В. Каков этот предел и насколько это возможно?
О. Этот предел обозначен формулой вычисления энтропии и для данного файла составляет до 1261269 бит. Это возможно, использовав длинную арифметику для арифметического кодирования этого файла. По сути ничего сложного.
В. И что нам это даст?
О. Еще раз подробно напишу алгоритм действий:
Мы взяли этот тестовый файл AMillionRandomDigits.bin длиною 415241 байт. Длина его бинарного файла (то есть двоичного) 3321928 бит.
Длина кода расположения АКС для него (ai1-locat.txt) 2286631 бит (292405 единиц и 1994226 нулей). Логарифм вероятности появления АКС — 2.96718368674378 при длине самого АКС три бита. Итого такой код сжимается по формуле Шеннона до 1261268.904 бит.
Затем мы АКС убираем, и записываем в оставшиеся после этого данные длиною 1994226 бит (ai2-field.txt) те же АКС в новом расположении и в новом количестве, с таким кодом, у которого логарифм вероятности появления АКС — равен длине АКС 3 бита. Для того чтобы так получилось это должно быть 284890 АКС среди 1994226 остальных знаков ai2-field.txt, такой новый код расположения имеет энтропию по формуле Шеннона 1238846.109 бит. (Причем этот код мы берем не произвольно, а из определенной части сжимаемых данных (например, код расположения одного из знаков восьмеричного кода имеет примерно такую же вероятность)).
При этом необходимо заметить, что не обязательно вероятность появления АКС в новом коде расположения должна быть _точно_ равна вышеуказанному параметру (0.125). Просто максимум функции сжатия достигается именно при равенстве логарифма вероятности появления АКС его длине.
Итого мы сокращаем -7515 АКС по 3 бита = -22545 бит.
Коды расположения уменьшились 1238846.109 — 1261268.904 = -22422.79479.
Разница составляет -123.9194967 бит суммарного уменьшения кода всех данных.
В. Ну и что это нам дает?
О. Сжатие данные на величину, превышающую их энтропию, позволяет производить их многократное повторное сжатие, преодолевая энтропийный предел сжатия данных. Простыми словами сжимать колоссальные массивы информации до определенного минимума.
В. И каков этот минимум?
О. По предварительным расчетам в пределах конкретного алгоритма данного способа сжатия до одного мегабайта.
В. В чем подвох?
О. Теоретические возможности, которые открываются при применении данного способа сжатия данных настолько выходят за рамки привычных представлений устоявшихся уже почти за сто лет, что даже серьезные специалисты вместо проверки самого (довольно несложного) алгоритма кодирования, предпочитают доказывать его теоретическую несостоятельность, несмотря на очевидные практические результаты.
lair
07.04.2015 11:16+4В. А вы что его сжали?
О. Пока нет
Этим все сказано про ваш алгоритм.
Математически он подтвержден? Нет.
Практически он подтвержден? Тоже нет.
Это возможно, использовав длинную арифметику для арифметического кодирования этого файла. По сути ничего сложного.
Что вы называете «длинной арифметикой» — конкретно, по пунктам? Если в этом нет ничего сложного, почему вы этого до сих пор не сделали?
очевидные практические результаты.
Где они?
Исходный файл имеет длину 415241 байт. Вы «разложили» его на файлы длиной 285828 байт и 290906 байт — суммарно 576734 байта, т.е. увеличив его размер в 1.4 раза.
ILIN-AIC Автор
07.04.2015 11:31Честно говоря ваш комментарий мне напоминает «не проверял но осуждаю» :)
"«Если в этом нет ничего сложного, почему вы этого до сих пор не сделали?»"
Дело в том что я собственно не программист. Так программирую помаленьку на бейсике для проверки своих теоретических изысканий. Сам арифметический кодер пока не писал и какая собственно необходима длинна арифметики не знаю. Поскольку помощи «от добрых людей» как с козла молока придется опять сделать самому :)
"«Где они?
Исходный файл имеет длину 415241 байт. Вы «разложили» его на файлы длиной 285828 байт и 290906 байт — суммарно 576734 байта, т.е. увеличив его размер в 1.4 раза. „“
Мы опять-таки упираемся необходимость арифметического кодирования кода расположения АКС — теоретически достижимой предела для которого 1261269 бит. Но и это не самое главное. Само по себе это нам ничего не дает. Все дело в дальнейшей замене этого кода на более короткий и соединение его с оставшимися знаками длиною 1994226 бит (ai2-field.txt).

lair
07.04.2015 11:36Честно говоря ваш комментарий мне напоминает «не проверял но осуждаю» :)
Почему же: я честно проверил размеры файлов.
Дело в том что я собственно не программист.
А кто вы? Математик? Data scientist? Специалист по шифрованию? Специалист по теории алгоритмов?
Сам арифметический кодер пока не писал и какая собственно необходима длинна арифметики не знаю.
Что такое «арифметический кодер»? Что он должен делать?
Мы опять-таки упираемся необходимость арифметического кодирования кода расположения АКС
Что такое «арифметическое кодирование»? Какими свойствами оно должно обладать, чтобы ваш алгоритм был успешен?
Все дело в дальнейшей замене этого кода на более короткий
Вы меня простите, но «замена кода на более короткий» — это и есть задача сжатия, которую вы, по вашим словам, решили. А получается, что чтобы решить вашу задачу, нужно решить задачу сжатия… для которой нет доказанного решения. Следовательно, нет доказанного решения и для вашей задачи.

0serg
07.04.2015 13:57+1Затем мы АКС убираем, и записываем в оставшиеся после этого данные длиною 1994226 бит (ai2-field.txt) те же АКС в новом расположении и в новом количестве, с таким кодом, у которого логарифм вероятности появления АКС — равен длине АКС 3 бита. Для того чтобы так получилось это должно быть 284890 АКС среди 1994226 остальных знаков ai2-field.txt, такой новый код расположения имеет энтропию по формуле Шеннона 1238846.109 бит.
Сдается мне у Вас в этой части будут проблемы. Распишите-ка её подробнее, поскольку без сжатия 2го файла суммарный объем данных = 3588523 бита > 3321928 исходных

ILIN-AIC Автор
07.04.2015 12:01“”Честно говоря ваш комментарий мне напоминает «не проверял но осуждаю» :)
Почему же: я честно проверил размеры файлов.””
Просто вы даже не дождались результатов работы программы, хотя сами меня постоянно подзуживали «выложите хоть что нибудь»…
“А кто вы? Математик? Data scientist? Специалист по шифрованию? Специалист по теории алгоритмов?”
Это трудно объяснить. Впрочем об этом у Азимова есть повесть «Профессия»
“Что такое «арифметический кодер»? Что он должен делать? Что такое «арифметическое кодирование»?”
Программа арифметического сжатия ru.wikipedia.org/wiki/Арифметическое_кодирование
“Какими свойствами оно должно обладать, чтобы ваш алгоритм был успешен?”
Не превышать теоретический предел сжатия данных по Шеннону (1261268.904 бит) более чем на 50 бит (1261268.904 + 50 бит)
“Вы меня простите, но «замена кода на более короткий» — это и есть задача сжатия, которую вы, по вашим словам, решили.”
Совершенно верно
“А получается, что чтобы решить вашу задачу, нужно решить задачу сжатия… для которой нет доказанного решения.”
Нет вы запутались. Нужно решить задачу энтропийного сжатия для которой ЕСТЬ доказанного решения :) Именно арифметическое кодирование способно достичь теоретического предела энтропийного сжатия. Просто как правило использует более короткую арифметику для ускорения процесса сжатия, что приводит к некоторым потерям в степени сжатия
“Следовательно, нет доказанного решения и для вашей задачи.”
Следовательно, ЕСТЬ доказанного решения и для вашей задачи :)
ru.wikipedia.org/wiki/Энтропийное_кодирование
ploop
07.04.2015 12:07offtop
Пользуйтесь, пожалуйста, вот такой кнопочкой
А то ведь читать невозможно…

lair
07.04.2015 12:13+1Просто вы даже не дождались результатов работы программы, хотя сами меня постоянно подзуживали «выложите хоть что нибудь»…
А что, ваша программа делает что-то кроме декодирования? Я же не ставлю под сомнение то, что она воссоздает правильный файл. Я просто говорю, что результаты вашего кодирования — которые вы предоставили, которые не имеют отношения к вашей программе — заранее не удовлетворяют задаче.
Именно арифметическое кодирование способно достичь теоретического предела энтропийного сжатия.
Не для всех входных данных. «Однако в случае равновероятного распределения символов, например для строки бит 010101…0101 длины s метод арифметического кодирования приближается к префиксному коду Хаффмана и даже может занимать на один бит больше». Каковы результаты сжатия традиционными алгоритмами для вашего потока позиций?
Возвращаемся к вопросу: каковы символы вашей входной азбуки и каковы их относительные вероятности? (я сейчас говорю о потоке позиций)

saboteur_kiev
07.04.2015 12:58Просто ситуация такая, что за кучей непонятных слов, не видно что именно ваша программа сделала.
Я вот например написал простенькую программу, которая декодирует этот millionrandomdigits.bin, после чего он rar-ом сжался на 200 байт сильнее, чем до, и в моей программе я точно знаю, что никакие данные не хранятся, то есть можно было бы алгоритм добавить в тот же rar, и он бы стал жать лучше.
Но я не уверен, что алгоритм сработает на другом наборе рандомных данных, поэтому не тороплюсь выкладывать результаты, хочу сперва собрать статистику.
У вас же еще даже первоначального надежного практического результата нет, а вы уже доказываете теорию.

lair
07.04.2015 13:19Для справки: сжатие бинарных файлов размером 285832 и 290908, полученных из ваших текстовых, парочкой разных архиваторов дает размер от 429080 до 443335 байт. «Не хватает» вам трех-четырех процентов. Где вы их собираетесь брать — вопрос интересный.

lair
07.04.2015 13:48И еще для информации — при сжатии одним и тем же архиватором исходного файла и суммы ваших файлов получается следующее:
- из исходного файла (415241) — 421084
- из суммы ваших файлов (576736) — 431771
Иными словами, ваше преобразование ухудшает сжатие, а не улучшает его.

0serg
07.04.2015 13:55+1Не превышать теоретический предел сжатия данных по Шеннону
Довольно забавно что Вы пишете пост посвященный опровержению теоремы Шеннона (она утверждает что битовый поток случайных данных сжать невозможно) но апеллируете в ходе своих построений к этой же теореме :)

ILIN-AIC Автор
07.04.2015 21:45-1Прочитал вечером все комментарии. Видимо идея слишком сложна для понимания. Что ж напишем модуль арифметического кодирования самостоятельно.
Специально для специалистов повторю постановку задачи:
Длина кода расположения АКС для него (ai1-locat.txt) 2286631 бит (292405 единиц и 1994226 нулей), а такой код сжимается по формуле Шеннона до 1261268.904 бит.
Необходимо при сжатии не превышать этот теоретический предел больше чем на 50 бит.
lair
07.04.2015 22:07Длина кода расположения АКС для него (ai1-locat.txt) 2286631 бит (292405 единиц и 1994226 нулей), а такой код сжимается по формуле Шеннона до 1261268.904 бит. Необходимо при сжатии не превышать этот теоретический предел больше чем на 50 бит.
В добрый путь. «Классический архиватор» дает на этом файле 1304632 бит. Вам надо выиграть всего-то 43 тысячи бит. Жалких три процента, как я и писал раньше.
ILIN-AIC Автор
08.04.2015 07:58""«Классический архиватор» дает на этом файле 1304632 бит.""
У меня пока выходит 1262576 бит. Нужно хотя бы 1261319. Надо выиграть всего-то 1257 бит.
Длина кода расположения АКС 2286631 бит. Необходимо уменьшить cжатый код на 1257 бит.
1257 / 2286631 = 0.000549717
Жалких 0.054971703 процента…

0serg
07.04.2015 22:08К сжатию ai1-locat.txt претензий у меня нет. Теоретически возможно. На практике Вы столько не выжмете, но теоретически — верно.
У меня претензии к сжатию ai2-field.txt. Если его не жать, то Вы проиграли. Потенциала сжатия в нем с ходу не очень видно. У Вас его сжатие расписано очень невнятно и сумбурно.
ILIN-AIC Автор
08.04.2015 08:04"«У меня претензии к сжатию ai2-field.txt. Если его не жать»"
А его и не нужно жать. В него записывают новый код расположения путем вставки АКС.
0serg
08.04.2015 09:20+1Если его не жать то как я уже писал выше, минимальный объем данных равен сжатому объему ai1-local (1261269 бит) и несжатому ai2-field (2327254 бит) = 3588523 бита в сумме > 3321928 исходных.

ILIN-AIC Автор
08.04.2015 09:24"«минимальный объем данных равен...»"
Но не учли сокращение данных на размер нового кода расположения…
0serg
08.04.2015 13:15+1Но не учли сокращение данных на размер нового кода расположения
1. Каких данных? ai2-field?
2. Какого сокращения? Распишите нормально в чем и за счет чего будет сокращение.
3. Что за «новый код расположения»? Почему его нет в выложенных Вами данных?

0serg
09.04.2015 10:45+1Что-то Вы притихли :). Уже сдались, или все еще пытаетесь осилить арифметический кодер?
Мой Вам совет: не возитесь а выложите данные которые уже «сжаты» за исключением этого самого последнего этапа сжатия с кодером. Предел в этом последним этапе довольно легко оценить и Вы не потратите время на реализацию кодера который все равно будет бесполезен
ILIN-AIC Автор
09.04.2015 21:47К сожалению отвлекли неотложные житейские проблемы.
«не возитесь а выложите данные которые уже «сжаты» за исключением этого самого последнего этапа сжатия с кодером. Предел в этом последним этапе довольно легко оценить»
Да скорее всего так и поступим. В таком случае будет очевидно что все упирается в сжатие кода расположения АКС. Жаль что в такой важный момент эта рабочая неделя фактически потеряна…

lair
07.04.2015 22:10… но мне все-таки интересно, какие в вашем исходном потоке есть символы, и какие у них вероятности.

ILIN-AIC Автор
08.04.2015 08:31В каком исходном потоке?

lair
08.04.2015 08:45Файла позиций.

ILIN-AIC Автор
08.04.2015 09:15Вы имеете в виду новый код расположения?

lair
08.04.2015 09:22Я имею в виду файл ai1-local

ILIN-AIC Автор
08.04.2015 09:38"«какие в вашем исходном потоке есть символы
…
файл ai1-local
»"
файл ai1-local.txt содержит только 2 символа — ноль и единицу
lair
08.04.2015 09:40Если так рассуждать, то любой бинарный файл содержит нули и единицы. Но я вот что-то не уверен, что Шенноновская формула (которая считает количество бит) рассчитана на такое применение.

ILIN-AIC Автор
08.04.2015 09:49"" я вот что-то не уверен, что Шенноновская формула (которая считает количество бит) рассчитана на такое применение""
:) Только если одних знаков меньше чем других
lair
08.04.2015 11:21Правда?
Вот вам код: 1110111011101110.
Содержит нули и единицы? Да.
Одних знаков меньше, чем других? Да.
Средняя битовая длина по формуле Шеннона? 0.81, что дает длину закодированного сообщения в 13 бит.
Казалось бы, выигрыш…
Вот только оптимальное кодирование этой последовательности занимает два (3) бита: 100. Потому что алфавит там, в реальности, из одного символа.
ILIN-AIC Автор
09.04.2015 21:57-1Вы абсолютно точно описали суть проблемы. Один и тот же код можно закодировать и более длинной и более короткой последовательностью.

dtestyk
08.04.2015 00:49если будете писать на .net, то System.Numerics.BigInteger вам в помощь
в python есть поддержка big int
может вам будет полезным: en.wikipedia.org/wiki/List_of_computer_algebra_systems
в частности, системы с поддержкой Arbitrary precision
range encoder:
- ezcodesample.com/reanatomy.html
- en.wikipedia.org/wiki/Range_encoding


MrGobus
«максимальная степень сжатия с помощью кодирования без потерь ограничивается энтропией источника. То есть, простыми словами — нельзя сжать данные больше, чем позволяет их энтропия»
Обожаю подобные обороты в научной литературе, простые слова раскрыли смысл сказанного на 100% =)
Когда то увлекался подобной темой, пробовал найти брешь между символьным представлением числа в разных системах исчисления и бинарным но к сожалению не смог отыграть ни бита. Зато сделал для себя много интересных открытий в бинарной логике =) и что улыбнуло я тоже проецировал мои результаты и выводы на масштабы вселенной и даже мелькала мысли о противостоянии богу =) В общем увлекательное это занятие скажу я Вам.
ILIN-AIC Автор
Стараюсь не противостоять, а помогать :)