Вейвлет-анализ. Часть 3 / forpes.ru

Главная
Вейвлет-анализ. Часть 3

Вейвлет-анализ. Часть 3 +16

14.06.2019 01:15

Scorobey 4 1700 Источник

Введение

При проведении CWT анализа средствами библиотеки PyWavelets (бесплатное программное обеспечение с открытым исходным кодом, выпущенное по лицензии MIT) возникают проблемы с визуализацией результата. Предложенная разработчиками тестовая программа по визуализации приведена в следующем листинге:

Листинг

 import pywt
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(-1, 1, 200, endpoint=False)
sig  = np.cos(2 * np.pi * 7 * t) + np.real(np.exp(-7*(t-0.4)**2)*np.exp(1j*2*np.pi*2*(t-0.4)))
widths = np.arange(1, 31)
cwtmatr, freqs = pywt.cwt(sig, widths, 'cmor1-1.5')
plt.imshow(cwtmatr, extent=[-1, 1, 1, 31], cmap='PRGn', aspect='auto',
             vmax=abs(cwtmatr).max(), vmin=-abs(cwtmatr).max())  # doctest: +SKIP
plt.show() # doctest: +SKIP

При работе с комплексными вейвлетами, например с 'cmor1-1.5', программа выдаёт ошибку:

File"C:\Users\User\AppData\Local\Programs\Python\Python36\lib\site-packages\matplotlib\image.py", line 642, in set_data
    raise TypeError("Image data cannot be converted to float")
TypeError: Image data cannot be converted to float

Указанная ошибка, а так же сложности с выбором масштаба (widths) для обеспечения необходимого временного разрешения, затрудняют, особенно для начинающих пользователей, изучение CWT анализа, что и побудило меня к написанию данной статьи учебного характера.

Целью настоящей публикации является рассмотрение применения нового модуля визуализации scaleogram для анализа простых и специальных сигналов, а так же при использовании методов нормализации, логарифмического масштабирования и синтеза, которые позволяют получить дополнительную информацию при анализе временных рядов.

В статье использована информация из публикации “A gentle introduction to wavelet for data analysis”. В приведенных в указанной публикации листингах примеров исправлены ошибки, и каждый листинг примера приведен к законченному виду, что позволяет его использовать без ознакомления с предыдущими. Для вейвлет – анализа специальных сигналов использованы данные из базы примеров PyWavelets.

Вейвлет-скалограмма — это двумерное представление одномерных данных. На ось X наносится время, а на ось Y — шкала – результат вейвлет — преобразования сигнала соответствующее значению амплитуды сигнала в момент времени X. Аналитическое значение такого графического отображения сигнала состоит в том, что разрешение по времени отображается на оси Y, что даёт дополнительную информацию о динамических свойствах сигнала.

Вейвлет — скалограммы простых сигналов

1. Косинусоида с гауссовой огибающей (Заменяя вейвлеты. можно исследовать зависимость временного разрешения от масштаба):

Листинг

from numpy import* 
from pylab import*
import scaleogram as scg 
import pywt
# Заменяя вейвлеты, можно исследовать зависимость временного разрешения от масштаба
# Без указания вейвлета программа использует вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
#Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time =arange(ns)
scales = scg.periods2scales( arange(1, 40) )
p1=10;
periodic1 = cos(2*pi/p1*time) * exp(-((time-ns/2)/200)**2)
fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9));  
lines = ax1.plot(periodic1); 
ax1.set_xlim(0, len(time))
ax1.set_title("Косинусоида с гаусовой огибающей")
fig1.tight_layout()
ax2 = scg.cws(periodic1, scales=scales, figsize=(6.9,2.9)); 
txt = ax2.annotate("p1=%s"%p1, xy=(100, 10), bbox=dict(boxstyle="round4", fc="w"))
tight_layout()
print("Вейвлет функция для преобразования сигнала:", scg.get_default_wavelet(), "(",
      pywt.ContinuousWavelet(scg.get_default_wavelet()).family_name, ")")
show()

Вейвлет функция для преобразования сигнала: cmor1-1.5 ( Complex Morlet wavelets )

Периодический сигнал теперь появляется в виде горизонтальной непрерывной полосы в точке Y = p1, интенсивность которой изменяется в зависимости от амплитуды периодического сигнала.

Наблюдается некоторая нечеткость в обнаружении, поскольку ширина полосы не равна нулю, это связано с тем, что вейвлеты не обнаруживают одну частоту, а скорее полосу. Данный эффект связан с полосой пропускания вейвлета.

2. Последовательно добавляются три импульса с возрастающим периодом (Для рассмотрения периодических вариации в разных масштабах: анализ мульти разрешения):

Листинг

from  numpy import* 
import pandas as pd 
from pylab import*
import scaleogram as scg 
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
# Без указания вейвлета программа использует вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
pulses = zeros(ns, dtype=float32)
steps  = linspace(0, ns, 8)
periods = [10, 20, 40]
for i in range(0,3):
    step_mask = (time > steps[i*2+1]) & (time < steps[i*2+2])
    pulses += cos(2*pi/periods[i]*time) * step_mask

fig1, ax1 = subplots(1, 1, figsize=(7,3));  
lines = ax1.plot(pulses); ax1.set_xlim(0, len(time)); 
ax1.set_title("Три импульса запускаются в разное время"); ax1.set_xlabel("Time")
fig1.tight_layout()

ax2 = scg.cws(pulses, scales=scales, figsize=(7,3))

for i in range(0, 3):
    txt = ax2.annotate("p%d=%ds"%(i+1,periods[i]), xy=(steps[i*2]+20, periods[i]), 
                       bbox=dict(boxstyle="round4", fc="w"))
    ax2.plot(steps[i*2+1]*np.ones(2), ax2.get_ylim(), '-w', alpha=0.5)
    ax2.plot(steps[i*2+2]*np.ones(2),   ax2.get_ylim(), '-w', alpha=0.5)
tight_layout()
show()

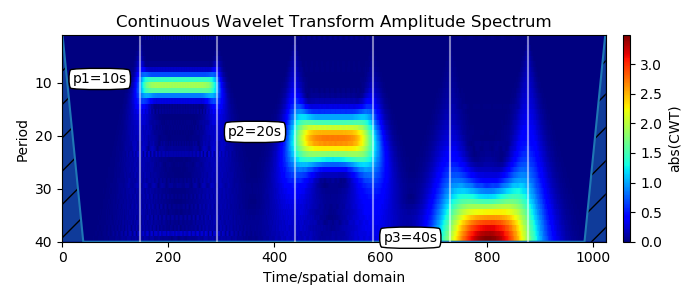
Импульсы появляются в ожидаемом месте Y, соответствующем их периодичности, они локализованы по частоте и во времени. Начало полосы и конец соответствуют импульсу.
Ширина полосы масштабируется с длиной периода. Это известное свойство вейвлет-преобразования: когда масштаб увеличивается, разрешение по времени уменьшается. Это также известно как компромисс между временем и частотой. Когда вы смотрите на спектрограмму такого типа, вы проводите много разрешающий анализ.

3. Три периодических колебания разной частоты одновременно (Вейвлет — анализ способен различить составляющие сигнала по частотам, если их отличия существенны):

Листинг

from  numpy import* 
import pandas as pd 
from pylab import*
import scaleogram as scg 
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
allwaves = np.zeros(ns, dtype=np.float32)
periods = [10, 20, 40]
for i in range(0,3):
    allwaves += cos(2*np.pi/periods[i]*time)

fig1, ax1 = subplots(1, 1, figsize=(6.5,2));  
lines = ax1.plot(allwaves); ax1.set_title("Три колебания одновременно") 
ax1.set_xlim(0, len(time)); ax1.set_xlabel("Время")
fig1.tight_layout()

ax2 = scg.cws(allwaves, scales=scales, figsize=(7,2))
tight_layout()
show()

4. Периодический сигнал не синусоидальной формы (Рассматривается отличие в вейвлет — преобразованиях сигнала треугольной формы с периодом 30 секунд от ранее рассмотренных):

Листинг

from  numpy import* 
from pylab import*
import scipy.signal
import scaleogram as scg 
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунд
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
ptri    = 30.0 # period in samples
raising = 0.8  # fraction of the period raising
triangle = scipy.signal.sawtooth(time/ptri*2*pi, raising)

# plot the signal 
fig1, ax1 = subplots(1, 1, figsize=(7,3));  
lines = ax1.plot(triangle); 
ax1.set_xlim(0, len(time))
ax1.set_title("triangle wave increasing 80% of the time with a 30s period")
fig1.tight_layout()

# and the scaleogram
ax2 = scg.cws(triangle, scales=scales, figsize=(7,3)); 
txt = ax2.annotate("first harmonic", xy=(100, 30), bbox=dict(boxstyle="round4", fc="w"))
txt = ax2.annotate("second harmonic", xy=(100, 15), bbox=dict(boxstyle="round4", fc="w"))
tight_layout()
show()

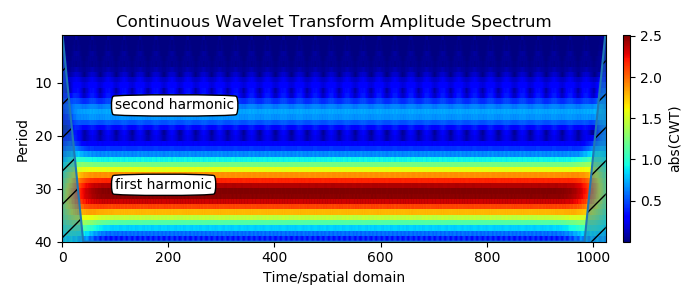
Большая полоса — это первая гармоника. Вторая гармоника видна ровно в половине значения периода первой гармоники. Это ожидаемый результат для периодических несинусоидальных сигналов. Нечеткие вертикальные элементы появляются вокруг второй гармоники, которая слабее и имеет амплитуду 1/4 от первой для сигнала треугольной формы.

5. Гладкие импульсы (гауссианы) схожи с реальными структурами данных. (В этом примере показано, как использовать вейвлет — анализ для обнаружения локализованных изменений сигнала во времени):

Серия гладких импульсов с различными значениями сигмы:

$2\cdot \sigma _{1}=2$
$2\cdot \sigma _{2}=10$
$2\cdot \sigma _{3}=20$

Ширина импульсов:

$\omega _{1}=2$
$\omega _{2}=20$
$\omega _{3}=100$

Листинг

from  numpy import* 
from pylab import*
import scaleogram as scg 
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
##Рассмотрим временную шкалу с 1 периодом / секунд
ns   = 1024
time = arange(ns)
scales = scg.periods2scales(arange(1, 40))
# несколько гауссовских импульсов с учетом сигмы
s1=1; s2=5; s3=10
events = [ns*0.1, ns*0.3, ns*0.7]
bumps = exp(-((time-events[0])/s1)**2) + exp(-((time-events[1])/s2)**2) +         exp(-((time-events[2])/s3)**2) 

# несколько шагов с учетом полуширины
w1=1; w2=5; w3= 50
steps = ((time > events[0]-w1) & (time < events[0]+w1)) +     ((time > events[1]-w2) & (time < events[1]+w2)) +     ((time > events[2]-w3) & (time < events[2]+w3))

# график импульсов
fig1, (ax1, ax2) = subplots(1, 2, figsize=(11, 2)); 
ax1.set_title("Bumps"); ax2.set_title("Steps")
lines = ax1.plot(bumps); ax1.set_xlim(0, len(time))
lines = ax2.plot(steps); ax2.set_xlim(0, len(time))
fig1.tight_layout()

# и скалограмма
scales_bumps = scg.periods2scales(arange(1, 120, 2) )
fig2, (ax3, ax4) = subplots(1, 2, figsize=(14,3));  
ax3 = scg.cws(bumps, scales=scales_bumps, ax=ax3)
ax4 = scg.cws(steps, scales=scales_bumps, ax=ax4)
for bmpw, stepw in [(2*s1, 2*w1), (2*s2,2*w2), (2*s3, 2*w3)]:
    ax3.plot(ax3.get_xlim(), bmpw*ones(2), 'w-', alpha=0.5)
    ax4.plot(ax4.get_xlim(), stepw*ones(2), 'w-', alpha=0.5)
fig2.tight_layout()
show()

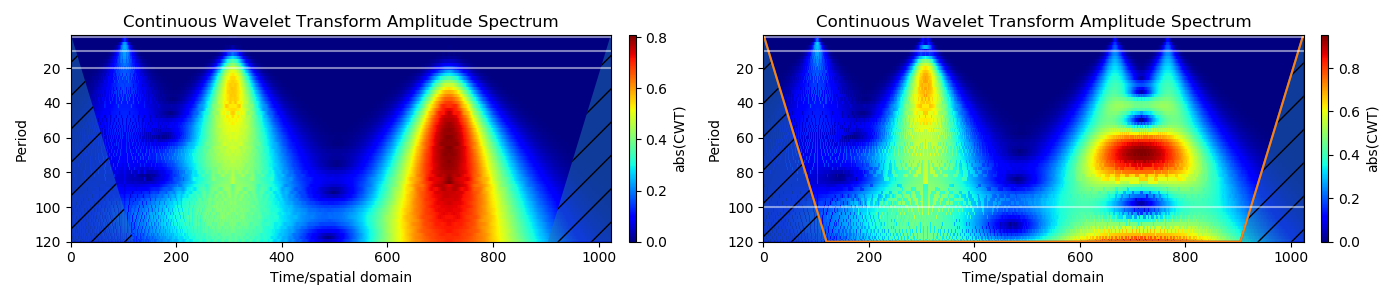
Дискретные импульсы создают конусообразные структуры на сиалограмме, которые также известны как конус влияния. Гладкие импульсы (гауссианы) схожи с реальными структурами данных и создают конусы, расширяющиеся в сторону больших масштабов. Горизонтальные направляющие линии приблизительно соответствуют периодам времени (2 с, 10 с, 20 с). Следовательно, импульс похож на периодический сигнал с одним периодом.

6. Шум (Отображение шума на сиалограмме):

Листинг

from numpy import* 
from pylab import*
import scaleogram as scg 
import random
scg.set_default_wavelet('cmor1-1.5')
# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
#Рассмотрим временную шкалу с 1 периодом / секунду
ns   = 1024
time =arange(ns)
scales = scg.periods2scales( arange(1, 40) )
noise =random.sample(range(ns), ns)


fig1, ax1 = plt.subplots(1, 1, figsize=(6.2,2));  
ax1.set_title("Последовательность псевдослучайных чисел")
lines = ax1.plot(time, noise) 
ax1.set_xlim(0, ns)
fig1.tight_layout()

ax2 = scg.cws(noise, scales=scales, figsize=(7,2))
tight_layout()
show()

Шум обычно отображается в виде набора элементов, а некоторые неровности могут выглядеть как объекты реальных данных, поэтому при использовании реальных данных необходимо соблюдать осторожность, и, при необходимости, проверить уровень шума. Верхний график будет отличатся при каждом запуске программы.

Вейвлет скалограммы специальных сигналов

В базе данных PyWavelets содержаться двадцать специальных сигналов вейвлет преобразования которых будут полезны как для изучения, так и для разработки. Поэтому приведу листинг позволяющий провести вейвлет анализ всех двадцати сигналов:

Листинг

#!/usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
from pylab import*
import scaleogram as scg 
import pywt
signals = pywt.data.demo_signal('list')
signal_length=1024
for signal in signals:
    if signal in ['Gabor', 'sineoneoverx']:
        x = pywt.data.demo_signal(signal)
    else:
        x = pywt.data.demo_signal(signal, signal_length)   
    times=[]
    signals=[]
    for time, sig in enumerate(x.real):
        times.append(time)
        signals.append(sig)
    scg.set_default_wavelet('cmor1-1.5')
    scales = scg.periods2scales( arange(1, 40) )
    fig1, ax1 = subplots(1, 1, figsize=(6.9,2.9));  
    lines = ax1.plot(signals); 
    ax1.set_xlim(0, len(times))
    ax1.set_title("%s"%signal)
    fig1.tight_layout()
    ax2 = scg.cws(signals, scales=scales, figsize=(6.9,2.9)); 
    tight_layout()
    show()

Приведу только один результат вейвлет преобразования Доплеровского сигнала:

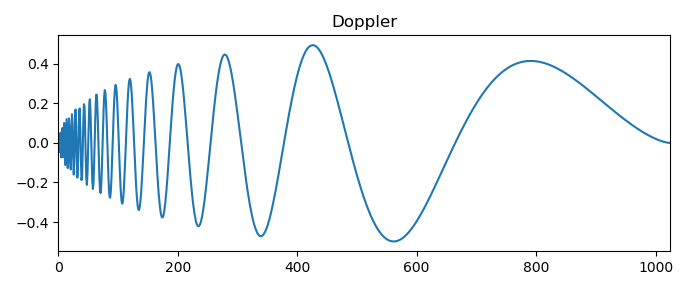
Рассмотрены наиболее распространённые разновидности простых и специальных сигналов, что позволяет перейти к использованию скалограммы для решения некоторых задач анализа временных рядов.

Вейвлет скалограммы временных рядов

1. CDC данные о рождаемости в США 1969-2008 (Данные о рождаемости содержат периодические особенности, как в годовом масштабе так и в меньшем):

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)

fig = figure(figsize=(12,2))
lines = plot(births.index, births.values/1000, '-')
xlim(datetime_lim)

ylabel("Nb of birthes [k]"); title("Total births per day in the US (CDC)");
xlim = xlim()

ax = scg.cws(births, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day")
set_x_yearly(ax, len(births))
show()

Горизонтальная линия появляется с периодичностью около 7 дней. Высокие значения появляются вблизи границ шкалы, что является нормальным поведением вейвлет — обработки. Эти эффекты хорошо известны как конус влияния, именно поэтому (необязательная) маска накладывается на эту область.

2. Нормализация (Удаление среднего значения -births_normed = births-births.mean() является обязательным, в противном случае границы данных рассматриваются как этапы, которые создают много ложных конусовидных обнаружений):

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
ax = scg.cws(births_normed, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day")
set_x_yearly(ax, len(births))
show()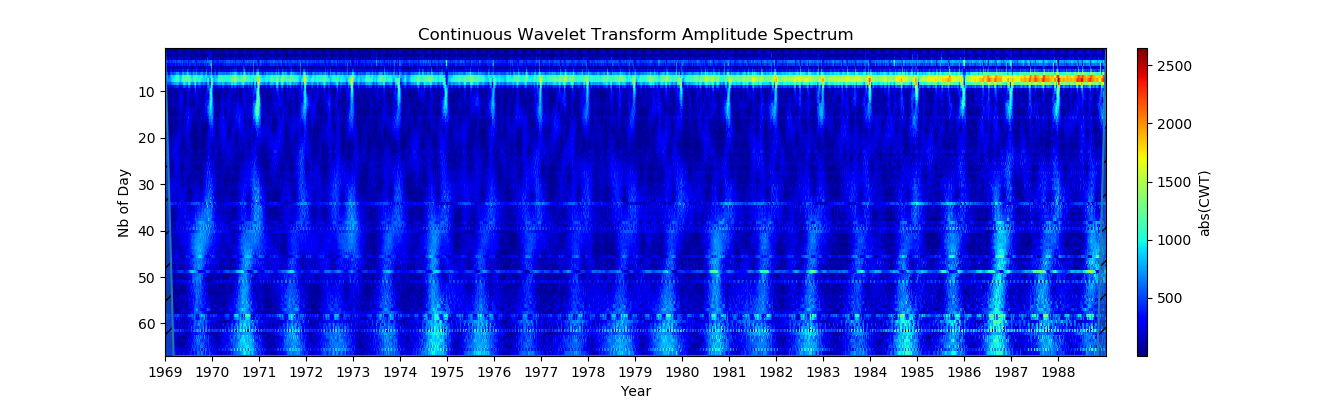

3. Cмена масштаба по амплитуде (Чтобы увидеть годовые объекты, с помощью period2scales () уточняется масштаб по оси Y.):

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
scales = scg.periods2scales(np.arange(1, 365+100, 3))
ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 5), xlabel="Year", ylabel="Nb of Day",
            clim=(0, 2500))
set_x_yearly(ax, len(births))
show()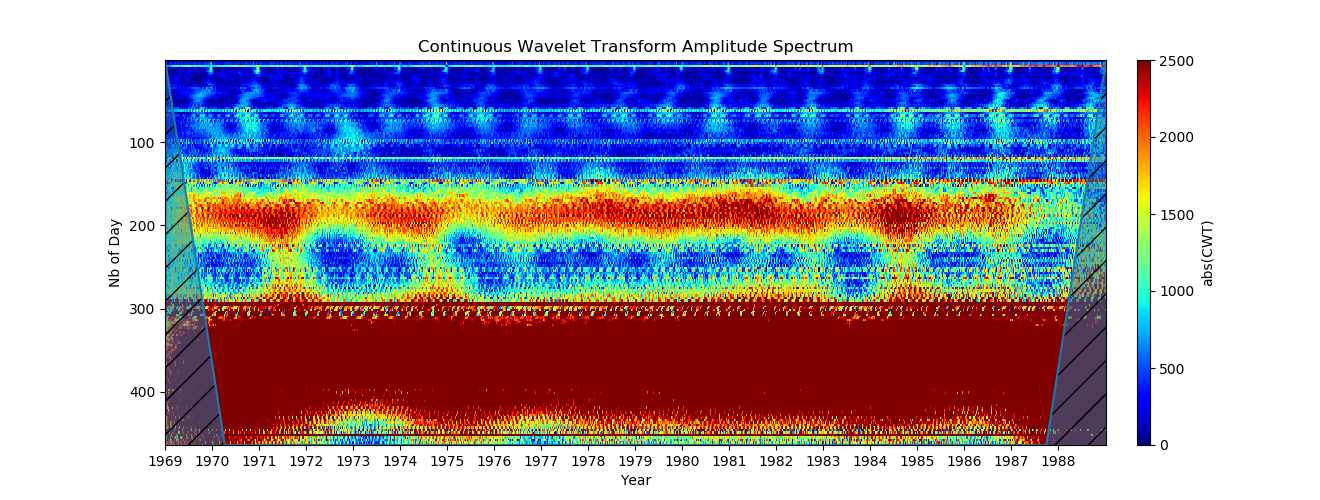

Диапазон амплитуд цветовой карты (ось Y) теперь задается параметром clim = (0,2500). Точное значение для амплитуды колебаний зависит от вейвлета, но будет оставаться близко к порядку действительного значения. Это намного лучше, теперь мы очень хорошо видим годовую вариацию, а также примерно 6 месяцев!

4. Использование логарифмической шкалы (Чтобы можно было видеть маленькие и большие периоды одновременно, лучше использовать логарифмическую шкалу на оси Y. Это достигается с помощью опции xscale = log.)

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
scales = scg.periods2scales(np.arange(1, 365+100, 3))
ax = scg.cws(births_normed, scales=scales, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))
print("Number of available days:", len(births_normed))
show()

Результат намного лучше, но теперь пиксели при низких значениях периодов вытянуты вдоль оси Y.

5. Равномерное распределение по логарифмической шкале( Чтобы получить однородное распределение по шкале, значения периода должно быть равномерно распределено, а затем преобразовано в значения шкалы, как показано ниже:):

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg 
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))

# сохранить CWT в объекте, чтобы избежать пересчета для следующих участков
cwt = scg.CWT(births_normed, scales=scales) 

ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))

bboxf = dict(boxstyle="round", facecolor="y", edgecolor="0.5")
arrowpropsf = dict(facecolor='yellow', shrink=0.05)
text = ax.annotate("unusual\nfeature", xy=(365*6, 15), xytext=(365*3, 50), 
                   bbox=bboxf, arrowprops=arrowpropsf)
show()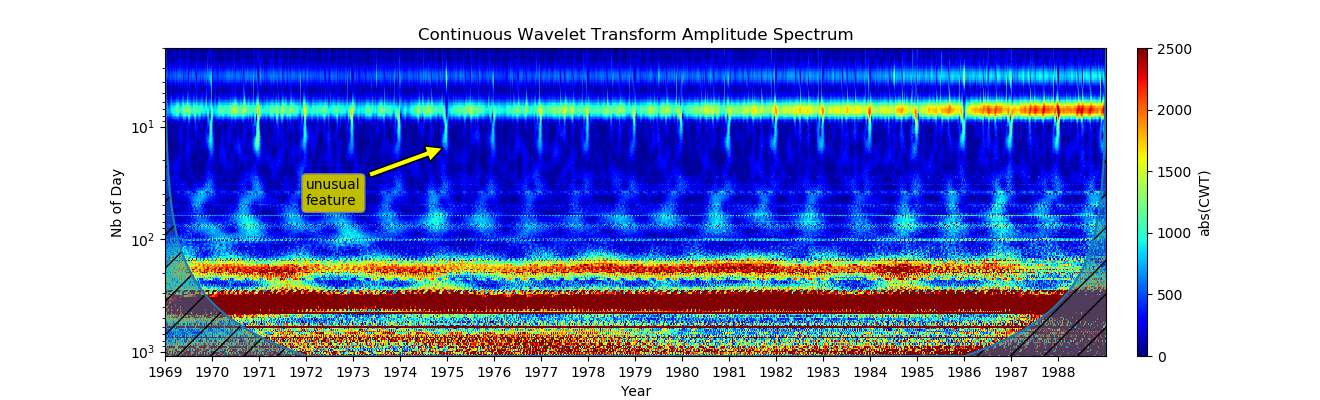

Мы можем видеть изменения сигнала на всех масштабах. Сиалограмма показывает каждый год в одинаковых периодах.

6. Выделение части шкалы времени (Проверка наличия промежуточных данных между отметками шкалы времени в поисках артефактов или отсутствующих данных.):

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg
import pywt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')

df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
cwt = scg.CWT(births_normed, scales=scales) 
# увеличить на два года: 1974-1976

fig = figure(figsize=(12,4))
lines =plot(births.index, births.values/1000, '-')
xlim(pd.to_datetime("1974-01-01"), pd.to_datetime("1976-01-01"))
ylabel("Nb of birthes [k]"); title("Total births per day bw 1974 and 1976");

# перерисовать предыдущую масштабограмму с увеличением
ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))
xlim = ax.set_xlim( (1974-1969)*365, (1976-1969)*365 )
show()

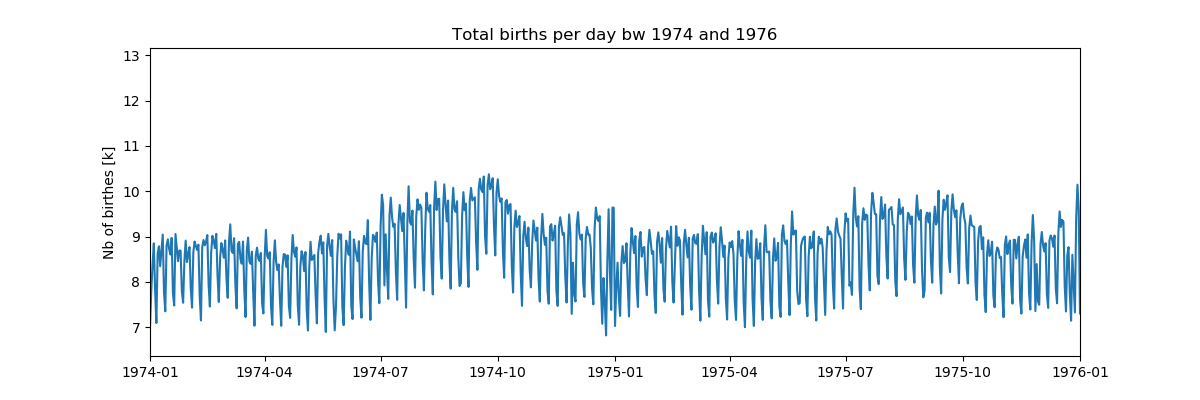
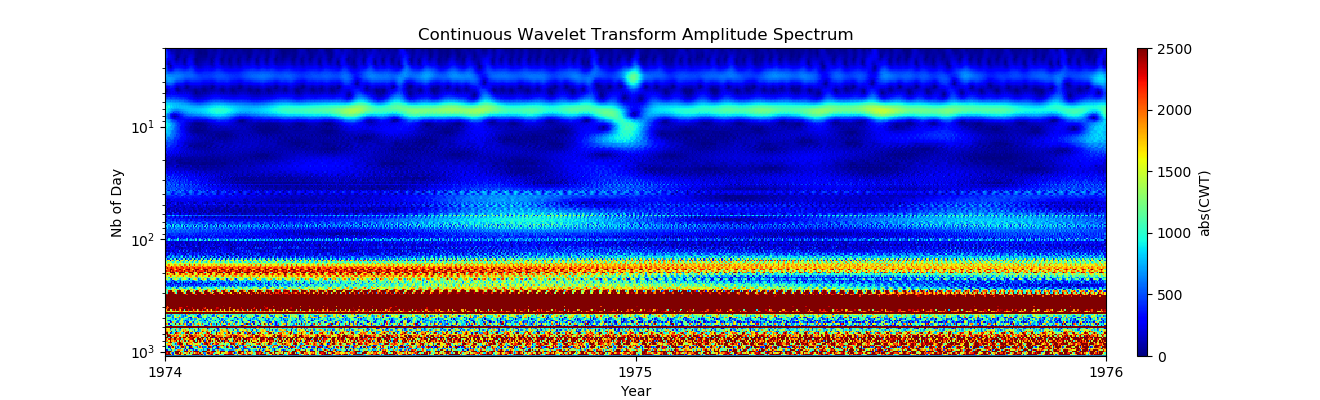
На первый взгляд, еженедельные модели выглядят очень равномерно, но что-то происходит на Рождество, давайте еще раз рассмотрим этот период:

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg
import pywt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
cwt = scg.CWT(births_normed, scales=scales) 
#Изменить масштабы: декабря 1975 года и января 1976 года
fig = figure(figsize=(12,4))
lines = plot(births.index, births.values/1000, '.-')
xlim(pd.to_datetime("1974-12-01"), pd.to_datetime("1975-02-01"))
ylabel("Nb of birthes [k]"); title("Total births per day : 2 monthes zoom");

# перерисовать предыдущую масштабограмму с увеличением
ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))
xlim = ax.set_xlim( (1975-1969)*365-30, (1975-1969)*365+30 )
show()

Теперь ясно, что это эффект конца года:

Рождество: 23/24/25 декабря показывает аномально низкое число рождений, и эти дни отклоняются от недельного графика;
Есть данные за декабрь, что согласуется с наличием некоторого значения для затронутых дат 1-е и 2-е января, в эти даты обычно меньше личных событий

7. Синтез (Сиалограмму строят из нормализованных данных, при лучшей читаемости для всех масштабов):

Листинг

import pandas as pd
import numpy as np 
from pylab import*
import scaleogram as scg
import pywt
from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

# Заменяя вейвлеты можно исследовать зависимость временного разрешения от масштаба
#По умолчанию используется вейвлет 'cmor1-1.5'
#scg.set_default_wavelet('cmor1-1.5')
#scg.set_default_wavelet('cgau5')
#scg.set_default_wavelet('cgau1')
#scg.set_default_wavelet('shan0.5-2')
#scg.set_default_wavelet('mexh')
df = pd.read_csv("births.csv")

#удалить аномальные данные 
df = df[(df.day>=1) & (df.day<=31) & (df.births.values > 1000)]

# преобразование дат
datetime = pd.to_datetime(df[['year', 'month', 'day']], errors='coerce')
df.insert(0, 'datetime', datetime)

datetime_lim = [ df.datetime.min(), df.datetime.max() ] 
years_lim = [ df.datetime.min().year, df.datetime.max().year ]
births = df[['datetime', 'births']].groupby('datetime').sum().squeeze()
def set_x_yearly(ax, days, start_year=1969):
    xlim  = (np.round([0, days]) / 365).astype(np.int32)
    ticks = np.arange(xlim[0], xlim[1])
    ax.set_xticks(ticks*365)
    ax.set_xticklabels(start_year + ticks)


births_normed = births-births.mean()
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
scales = scg.periods2scales(np.logspace(np.log10(2), np.log10(365*3), 200))
# использовать значения логарифмических интервалов при использовании оси log-Y-axis :-)
cwt = scg.CWT(births_normed, scales=scales) 
ax  = scg.cws(cwt, figsize=(13.2, 4), xlabel="Year", ylabel="Nb of Day", 
             clim=(0,2500), yscale='log')
set_x_yearly(ax, len(births))

bbox = dict(boxstyle="round", facecolor="w", edgecolor="0.5")
bbox2 = dict(boxstyle="round", facecolor="y", edgecolor="0.5")
arrowprops = dict(facecolor='white', shrink=0.05)
arrowprops2 = dict(facecolor='yellow', shrink=0.05)
for period, label in [ (3.5, "half a week"), (7, "one week"), (365/2, "half a year"), 
                      (365, "one year"), (365*2.8, "long trends")]:
    text = ax.annotate(label, xy=(365*5.5, period), xytext=(365*2, period), 
                       bbox=bbox, arrowprops=arrowprops)
text = ax.annotate("end of year\neffect", xy=(365*6, 15), xytext=(365*3, 50), 
                   bbox=bbox2, arrowprops=arrowprops2)
text = ax.annotate("increase in\nvariations *amplitude*", xy=(365*18.5, 7), xytext=(365*14, 50), 
                   bbox=bbox2, arrowprops=arrowprops2)
show()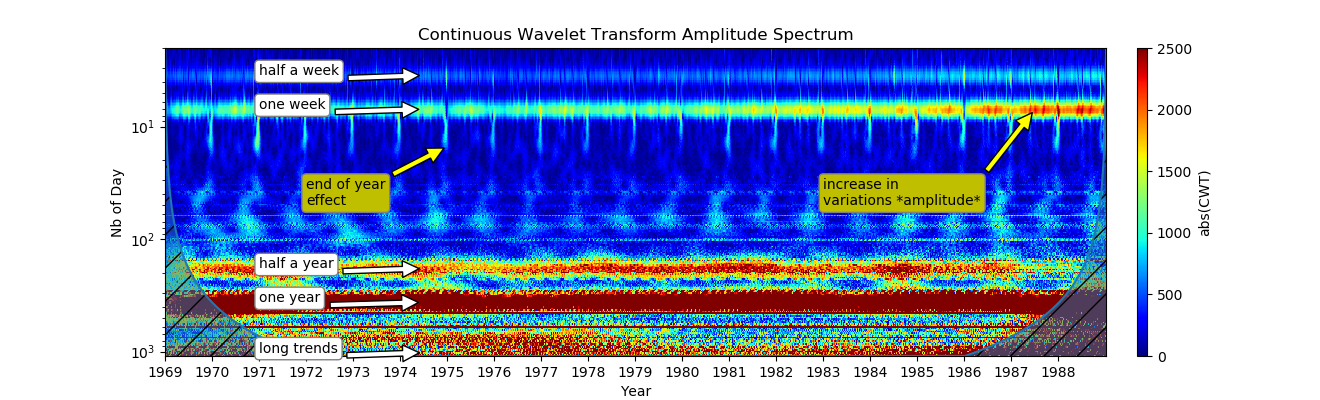

CWT раскрывает много информации за короткий промежуток времени:

Еженедельная вариация, показывающая привычки в больницах, присутствует в течение нескольких десятилетий;

В 80-х годах наблюдается увеличение недельного показателя, который может быть вызван изменением рабочих привычек больниц, изменением рождаемости или простым изменением населения;

Вторая полоса в полугодии — это явно вторая гармоника. Нечеткие модели появляются в зоне от 3 до 1 месяца, что может быть связано с третьей гармоникой, поскольку годовые колебания настолько сильны. Это также может быть вызвано влиянием праздников на рождаемость и может потребовать дальнейшего изучения;

Эффект конца года был отмечен на Рождество и 1 января. Этот, возможно, остался невидимым с другим частотным методом.

Выводы:

В этой публикации мы увидели, как базовый вид вариаций сигнала переводится на скалограмму. Затем был использован пример упорядоченного по времени набора данных, чтобы шаг за шагом продемонстрировать, как CWT применяется к стандартным данным.

Приведенная методика может быть расширена для анализа сетевого трафика и для обнаружения необычного поведения объектов. CWT — это мощный инструмент, который все чаще используется в качестве входных данных для нейронных сетей и может использоваться для создания новых функций с целью классификации или обнаружения аномалий.

Каждый пример реализован в виде самостоятельной программы, что позволяет выбрать пример под свою задачу, не вникая в предыдущие и последующие примеры. Пользователь может попробовать любые вейвлет – функции из списка приведенного в начале каждой программы, например, такие как mexh или gaus5. Для примера 1 соответственно:

P.S. Для практического использования листингов приведу версии используемых в них модулей:

>>> import scaleogram; print(scaleogram .__version__)
0.9.5
>>> import pandas; print(pandas .__version__)
0.24.1
>>> import numpy; print(numpy .__version__)
1.16.1
>>> import  matplotlib; print(matplotlib .__version__)
3.0.2

Для самостоятельного набора данных в файл *.csv привожу структуру данных(в одном столбце):
year,month,day,gender,births
1969,1,1,F,4046
1969,1,1,M,4440
1969,1,2,F,4454
1969,1,2,M,4548
…
Для версии 0.24.1 pandasс потребуется явно регистрировать конвертеры matplotlib.

Чтобы зарегистрировать конвертеры:

from pandas.plotting import register_matplotlib_converters
register_matplotlib_converters()

Комментарии (4)

robomakerr
15.06.2019 14:16
#20284002
Импульсы появляются в ожидаемом месте Y, соответствующем их периодичности, они локализованы по частоте и во времени.

Правильно ли я понимаю, что фурье-анализ со скользящим окном, равным наименьшему периоду в импульсе, покажет почти то же самое?
1. Scorobey Автор
  15.06.2019 16:43
  #20284250
  Оконное Фурье не адаптирует окно к частоте и работает либо на высоких частотах, либо на низких, а вейвлет работает на обеих частотах.
  1. robomakerr
    16.06.2019 11:07
    #20285490
    Вы не могли бы подробнее развернуть свой ответ? Если мои позабытые школьные знания не подводят, фурье «работает» на всех частотах, больших 1/Т, где Т — ширина окна.
    
    Scorobey Автор
    16.06.2019 12:13
    #20285600
    Лучше всего показать на примере в котором и Вы примите участие.Вот функция для быстрого (оконного фурье -STFT):
    from scipy import*
    from pylab import*
    def stft(x, fs, framesz, hop):
    framesamp = int(framesz*fs)
    hopsamp = int(hop*fs)
    w = hanning(framesamp)
    X = array([fft(w*x[i:i+framesamp])
    for i in range(0, len(x)-framesamp, hopsamp)])
    return X
    Вот пример её запуска для низкой частоты:
    f0 = 440 #Вычислить STFT синусоиды 440 Гц
    fs = 8000 # дискретизация на частоте 8 кГц
    T = 5 # продолжительностью 5 секунд
    framesz = 0.050 # с размером кадра 50 миллисекунд
    hop = 0.025 # и размер прыжка 25 миллисекунд.
    Вот интерфейс вывода в спектрограмму (не путать со скалограммой) с заданием спектра:
    t = linspace(0, T, T*fs, endpoint=False)
    x =sin(2*pi*f0*t)+sin(4*pi*f0*t)
    X = stft(x, fs, framesz, hop)
    imshow(absolute(X.T), origin='lower', aspect='auto',
    interpolation='nearest')
    xlabel('Time')
    ylabel('Frequency')
    show()
    Теперь сгенерируйте два нестационарных сигнала — один с двумя одновременно действующими частотами другой с теми же частотами но следующими по времени.
    Посмотрите на спектрограммы и всё поймёте — это лучший способ убедится во всём самому и заодно и вспомнить школьный курс. Да окно и перекрытие не меняется во время анализа а устанавливается для заданной частоты.
    Спасибо за вопрос!!!

Вейвлет-анализ. Часть 3 +16

Введение

Вейвлет — скалограммы простых сигналов

Вейвлет скалограммы специальных сигналов

Вейвлет скалограммы временных рядов

Выводы:

Комментарии (4)

robomakerr

Scorobey Автор

robomakerr

Scorobey Автор