Введение
Рассмотрим дискретное вейвлет – преобразования (DWT), реализованное в библиотеке PyWavelets PyWavelets 1.0.3. PyWavelets — это бесплатное программное обеспечение с открытым исходным кодом, выпущенное по лицензии MIT.
При обработке данных на компьютере может выполняться дискретизированная версия непрерывного вейвлет-преобразования, основы которого описаны в моей предыдущей статье. Однако, задание дискретных значений параметров (a,b) вейвлетов с произвольным шагом ?a и ?b требует большого числа вычислений.
Кроме того, в результате получается избыточное количество коэффициентов, намного превосходящее число отсчетов исходного сигнала, которое не требуется для его реконструкции.
Дискретное вейвлет – преобразование (DWT), реализованное в библиотеке PyWavelets, обеспечивает достаточно информации как для анализа сигнала, так и для его синтеза, являясь вместе с тем экономным по числу операций и по требуемой памяти.
Когда нужно использовать вейвлет-преобразование вместо преобразования Фурье
Преобразования Фурье будет работать очень хорошо, когда частотный спектр стационарный. При этом частоты, присутствующие в сигнале, не зависят от времени, и сигнал содержит частоты xHz, которые присутствует в любом месте сигнала. Чем нестационарнее сигнал, тем хуже будут результаты. Это проблема, так как большинство сигналов, которые мы видим в реальной жизни, нестационарны по своей природе.
Преобразование Фурье имеет высокое разрешение в частотной области, но нулевое разрешение во временной области. Покажем это на следующих двух примерах.
import numpy as np
from scipy import fftpack
from pylab import*
N=100000
dt = 1e-5
xa = np.linspace(0, 1, num=N)
xb = np.linspace(0, 1/4, num=N/4)
frequencies = [4, 30, 60, 90]
y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb)
y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb)
y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb)
y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb)
def spectrum_wavelet(y):
Fs = 1 / dt # sampling rate, Fs = 0,1 MHz
n = len(y) # length of the signal
k = np.arange(n)
T = n / Fs
frq = k / T # two sides frequency range
frq = frq[range(n // 2)] # one side frequency range
Y = fftpack.fft(y) / n # fft computing and normalization
Y = Y[range(n // 2)] / max(Y[range(n // 2)])
# plotting the data
subplot(2, 1, 1)
plot(k/N , y, 'b')
ylabel('Amplitude')
grid()
# plotting the spectrum
subplot(2, 1, 2)
plot(frq[0:140], abs(Y[0:140]), 'r')
xlabel('Freq')
plt.ylabel('|Y(freq)|')
grid()
y= y1a + y2a + y3a + y4a
spectrum_wavelet(y)
show()
show()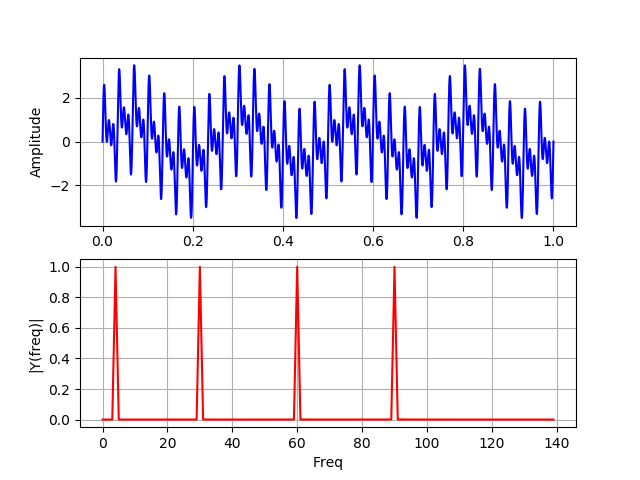
На этом графике все четыре частоты присутствуют в сигнале в течении всего времени его действия.
import numpy as np
from scipy import fftpack
from pylab import*
N=100000
dt = 1e-5
xa = np.linspace(0, 1, num=N)
xb = np.linspace(0, 1/4, num=N/4)
frequencies = [4, 30, 60, 90]
y1a, y1b = np.sin(2*np.pi*frequencies[0]*xa), np.sin(2*np.pi*frequencies[0]*xb)
y2a, y2b = np.sin(2*np.pi*frequencies[1]*xa), np.sin(2*np.pi*frequencies[1]*xb)
y3a, y3b = np.sin(2*np.pi*frequencies[2]*xa), np.sin(2*np.pi*frequencies[2]*xb)
y4a, y4b = np.sin(2*np.pi*frequencies[3]*xa), np.sin(2*np.pi*frequencies[3]*xb)
def spectrum_wavelet(y):
Fs = 1 / dt # sampling rate, Fs = 0,1 MHz
n = len(y) # length of the signal
k = np.arange(n)
T = n / Fs
frq = k / T # two sides frequency range
frq = frq[range(n // 2)] # one side frequency range
Y = fftpack.fft(y) / n # fft computing and normalization
Y = Y[range(n // 2)] / max(Y[range(n // 2)])
# plotting the data
subplot(2, 1, 1)
plot(k/N , y, 'b')
ylabel('Amplitude')
grid()
# plotting the spectrum
subplot(2, 1, 2)
plot(frq[0:140], abs(Y[0:140]), 'r')
xlabel('Freq')
plt.ylabel('|Y(freq)|')
grid()
y = np.concatenate([y1b, y2b, y3b, y4b])
spectrum_wavelet(y)
show()
show()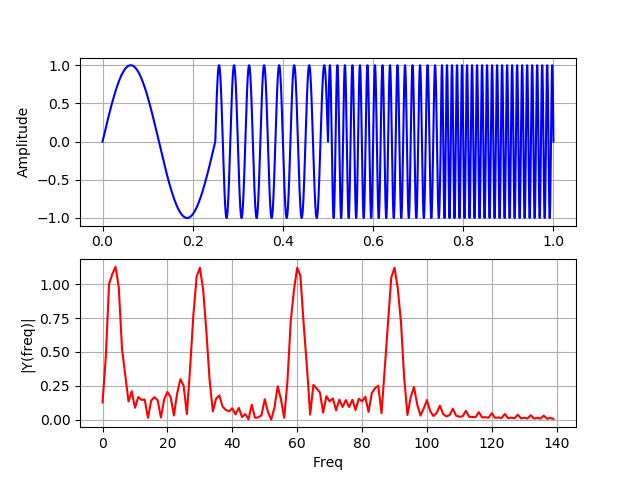
На этом графике сигналы не перекрываются во времени, боковые лепестки обусловлены разрывом между четырьмя различными частотами.
Для двух частотных спектров, содержащих точно такие же четыре пика, преобразование Фурье не может определить, где в сигнале эти частоты присутствуют. Лучшим подходом для анализа сигналов с динамическим частотным спектром является вейвлет-преобразования.
Основные свойства вейвлетов
Выбор типа, а следовательно свойств вейвлета, зависит от поставленной задачи анализа, например, для определения действующих значений токов в электроэнергетике большую точность обеспечивают вейвлеты Ингрид Добеши больших порядков. Свойства вейвлетов можно получить используя функцию pywt.DiscreteContinuousWavelet() в следующем листинге:
import pywt
from pylab import *
from numpy import *
discrete_wavelets = ['db5', 'sym5', 'coif5', 'haar']
print('discrete_wavelets-%s'%discrete_wavelets )
st='db20'
wavelet = pywt.DiscreteContinuousWavelet(st)
print(wavelet)
i=1
phi, psi, x = wavelet.wavefun(level=i)
subplot(2, 1, 1)
title("График самой вейвлет - функции -%s"%st)
plot(x,psi,linewidth=2, label='level=%s'%i)
grid()
legend(loc='best')
subplot(2, 1, 2)
title("График первообразной -функции -%s"%st)
plt.plot(x,phi,linewidth=2, label='level=%s'%i)
legend(loc='best')
grid()
show()Получим:
discrete_wavelets-['db5', 'sym5', 'coif5', 'haar']
Wavelet db20
Family name: Daubechies
Short name: db
Filters length: 40
Orthogonal: True
Biorthogonal: True
Symmetry: asymmetric
DWT: True
CWT: False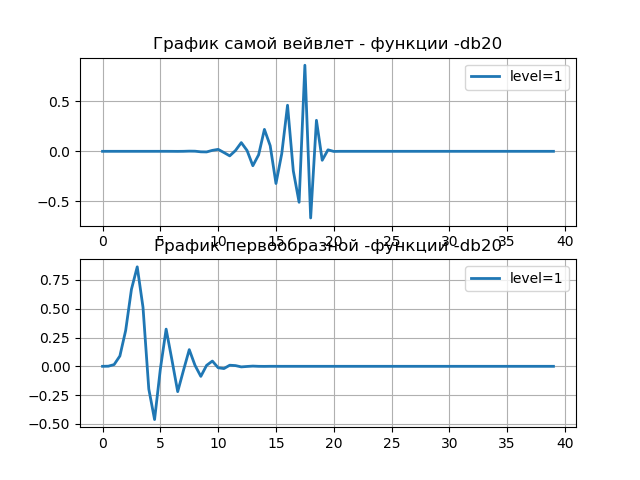
В ряде практических случаев возникает необходимость получить информацию о центральной частоте psi вейвлет – функции, которая используется, например, при вейвлет-анализе сигналов для выявления дефектов в зубчатых передачах:
import pywt
fс=pywt.central_frequency('haar', precision=8 )
print(fс)
# или так:
scale=1
fс1=pywt.scale2frequency('haar',scale)
print(fс1)0.9961089494163424
0.9961089494163424Пользуясь центральной частотой материнского вейвлета и масштабным коэффициентом «a» можно преобразовывать шкалы в псевдо частоты используя уравнение:
Режимы расширения сигнала
Перед вычислением дискретного вейвлет-преобразования с использованием банков фильтроввозникает необходимость удлинить сигнал. В зависимости от метода экстраполяции, на границах сигнала могут возникнуть существенные артефакты, приводящие к неточностям DWT преобразования.
PyWavelets предоставляет несколько методов экстраполяции сигнала, которые могут быть использованы для минимизации указанного негативного эффекта. Для демонстрации таких методов используем следующий листинг:
import numpy as np
from matplotlib import pyplot as plt
from pywt._doc_utils import boundary_mode_subplot
# synthetic test signal
x = 5 - np.linspace(-1.9, 1.1, 9)**2
# Create a figure with one subplots per boundary mode
fig, axes = plt.subplots(3, 3, figsize=(10, 6))
plt.subplots_adjust(hspace=0.5)
axes = axes.ravel()
boundary_mode_subplot(x, 'symmetric', axes[0], symw=False)
boundary_mode_subplot(x, 'reflect', axes[1], symw=True)
boundary_mode_subplot(x, 'periodic', axes[2], symw=False)
boundary_mode_subplot(x, 'antisymmetric', axes[3], symw=False)
boundary_mode_subplot(x, 'antireflect', axes[4], symw=True)
boundary_mode_subplot(x, 'periodization', axes[5], symw=False)
boundary_mode_subplot(x, 'smooth', axes[6], symw=False)
boundary_mode_subplot(x, 'constant', axes[7], symw=False)
boundary_mode_subplot(x, 'zeros', axes[8], symw=False)
plt.show()
На графиках показано, как короткий сигнал (красный) расширяется (черный) за пределами своей первоначальной протяженности.
Дискретное вейвлет – преобразование
Для демонстрации DWT будем использовать сигнал с динамическим частотным спектром, который со временем увеличивается. Начало сигнала содержит низкочастотные значения, а конец сигнала содержит частоты коротковолнового диапазона. Это позволяет нам легко определить, какая часть частотного спектра отфильтрована, просто взглянув на временную ось:
from pylab import *
from numpy import*
x = linspace(0, 1, num=2048)
chirp_signal = sin(250 * pi * x**2)
fig, ax = subplots(figsize=(6,1))
ax.set_title("Сигнал с динамическим частотным спектром ")
ax.plot(chirp_signal)
show()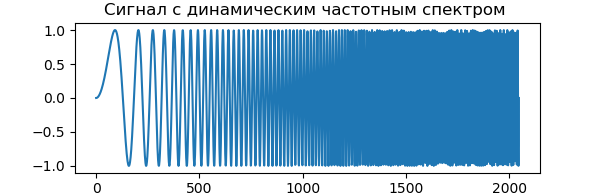
Дискретное вейвлет-преобразование в PyWavelets 1.0.3 это функция pywt.dwt(), которая вычисляет аппроксимирующие коэффициенты cA и детализирующие коэффициенты cD первого уровня вейвлет-преобразования сигнала, заданного вектором:
import pywt
from pylab import *
from numpy import *
x = linspace (0, 1, num = 2048)
y = sin (250 * pi * x**2)
st='sym5'
(cA, cD) = pywt.dwt(y,st)
subplot(2, 1, 1)
plot(cA,'b',linewidth=2, label='cA,level-1')
grid()
legend(loc='best')
subplot(2, 1, 2)
plot(cD,'r',linewidth=2, label='cD,level-1')
grid()
legend(loc='best')
show()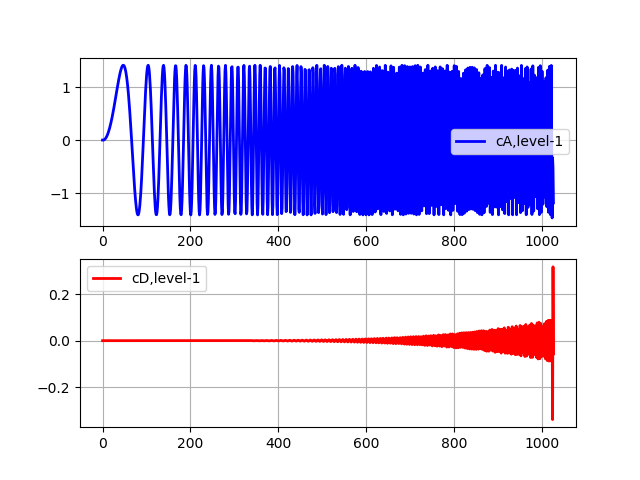
import pywt
from pylab import *
from numpy import *
x = linspace (0, 1, num = 2048)
y = sin (250 * pi * x**2)
st='sym5'
(cA, cD) = pywt.dwt(y,st)
(cA, cD) = pywt.dwt(cA,st)
(cA, cD) = pywt.dwt(cA,st)
(cA, cD) = pywt.dwt(cA,st)
(cA, cD) = pywt.dwt(cA,st)
subplot(2, 1, 1)
plot(cA,'b',linewidth=2, label='cA,level-5')
grid()
legend(loc='best')
subplot(2, 1, 2)
plot(cD,'r',linewidth=2, label='cD,level-5')
grid()
legend(loc='best')
show()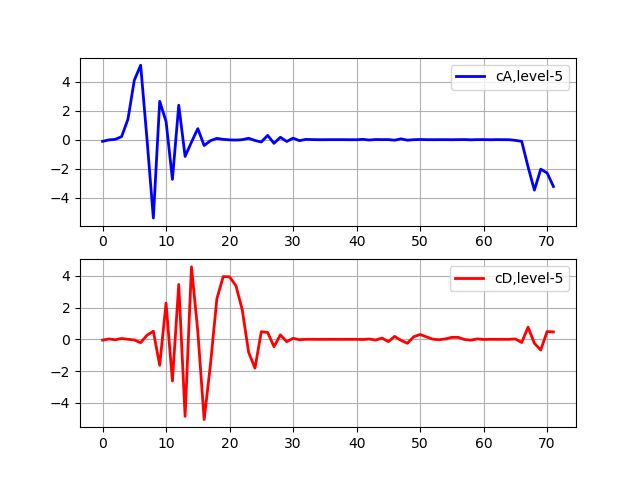
Коэффициенты аппроксимации (cA) представляют выход фильтра нижних частот (фильтра усреднения) DWT. Коэффициенты детализации (cD) представляют выход фильтра высоких частот (разностного фильтра) DWT.
Можно использовать функцию pywt.wavedec()для немедленного расчета коэффициентов более высокого уровня. Эта функция принимает за вход исходный сигнал и уровень и возвращает один набор коэффициентов аппроксимации (n-го уровня) и n наборов коэффициентов детализации (от 1 до n-го уровня). Вот пример для пятого уровня:
from pywt import wavedec
from pylab import *
from numpy import *
x = linspace (0, 1, num = 2048)
y = sin (250 * pi * x**2)
st='sym5'
coeffs = wavedec(y, st, level=5)
subplot(2, 1, 1)
plot(coeffs[0],'b',linewidth=2, label='cA,level-5')
grid()
legend(loc='best')
subplot(2, 1, 2)
plot(coeffs[1],'r',linewidth=2, label='cD,level-5')
grid()
legend(loc='best')
show()В результате получаем те же графики, что и в предыдущем примере. Можно получить отдельно коэффициенты cA и cD:
Для cA:
import pywt
from pylab import *
from numpy import*
x = linspace (0, 1, num = 2048)
data = sin (250 * pi * x**2)
coefs=pywt.downcoef('a', data, 'db20', mode='symmetric', level=1)Для cD:
import pywt
from pylab import *
from numpy import*
x = linspace (0, 1, num = 2048)
data = sin (250 * pi * x**2)
coefs=pywt.downcoef('d', data, 'db20', mode='symmetric', level=1)
Банк фильтров
Часть вопросов, касающихся уровней преобразования, мы рассмотрели в предыдущем разделе. Однако, DWT всегда реализуется как банк фильтров в виде каскада высокочастотных и низкочастотных фильтров. Банки фильтров являются очень эффективным способом разделения сигнала на несколько частотных поддиапазонов.
На первом этапе с малым масштабом анализируя высокочастотное поведение сигнала. На втором этапе шкала увеличивается с коэффициентом два (частота уменьшается с коэффициентом два), и мы анализируем поведение около половины максимальной частоты. На третьем этапе масштабный фактор равен четырем, и мы анализируем частотное поведение около четверти максимальной частоты. И это продолжается до тех пор, пока мы не достигнем максимального уровня разложения.
Максимальный уровень декомпозиции можно вычислить при помощи функции pywt.wavedec(), при этом декомпозиция и детализация будет иметь вид:
import pywt
from pywt import wavedec
from pylab import *
from numpy import*
x = linspace (0, 1, num = 2048)
data= sin (250 * pi * x**2)
n_level=pywt.dwt_max_level(len(data), 'sym5')
print('Максимальный уровень декомпозиции: %s'%n_level)
x = linspace (0, 1, num = 2048)
y = sin (250 * pi * x**2)
st='sym5'
coeffs = wavedec(y, st, level=7)
subplot(2, 1, 1)
plot(coeffs[0],'b',linewidth=2, label='cA,level-7')
grid()
legend(loc='best')
subplot(2, 1, 2)
plot(coeffs[1],'r',linewidth=2, label='cD,level-7')
grid()
legend(loc='best')
show()
Получим:
Максимальный уровень декомпозиции: 7
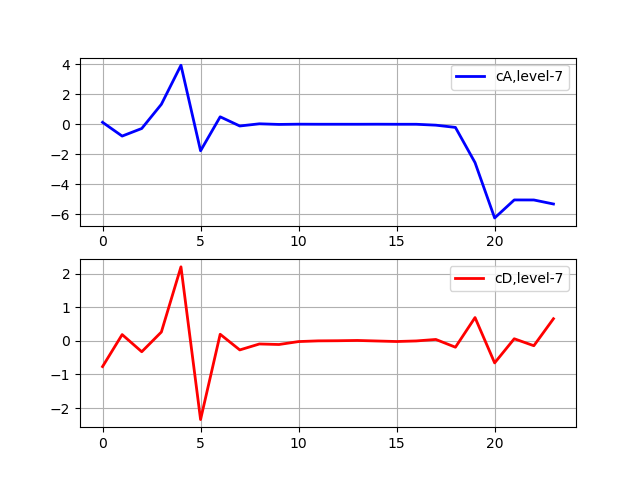
Декомпозиция останавливается, когда сигнал становится короче, чем длина фильтра для данного вейвлета sym5. Для примера предположим, что у нас есть сигнал с частотами до 1000 Гц. На первом этапе мы разделяем наш сигнал на низкочастотную и высокочастотную части, т. е. 0-500 Гц и 500-1000 Гц. На втором этапе мы берем низкочастотную часть и снова разделяем ее на две части: 0-250 Гц и 250-500 Гц. На третьем этапе мы разделили часть 0-250 Гц на часть 0-125 Гц и часть 125-250 Гц. Это продолжается до тех пор, пока мы не достигнем максимального уровня декомпозиции.
Анализ wav файлов с использованием fft Фурье и вейвлет скалограммы
Для анализа воспользуемся файлом WebSDR. Рассмотрим анализ приведенного сигнала средствами triang из scipy.signal и реализацию дискретного преобразования Фурье в python (fft из scipy.fftpack). Если длина последовательности fft не будет равна 2n, то вместо быстрого преобразования Фурье (fft) будет выполняться дискретное преобразование Фурье (dft). Именно таким образом работает эта команда.
Используем буфер быстрого преобразования Фурье по следующей схеме (численные данные для примера):
fftbuffer=np.zeros(15); создаем буфер, заполненный нулям;
fftbuffer [:8]=x [7:]; перемещаем конец сигнала в первую часть буфера; fftbuffer [8:]=x [:7]—перемещаем начало сигнала в последнюю часть буфера; X=fft(fftbuffer) — считаем преобразование Фурье буфера, заполненного значениями сигнала.
Чтобы фазовый спектр был более читаем, применим развертывание фазы. Для этого изменим строку с расчетом фазовой характеристики: pX=np.unwrap(np.angle(X)).
import numpy as np
from pylab import *
from scipy import *
import scipy.io.wavfile as wavfile
M=501
hM1=int(np.floor((1+M)/2))
hM2=int(np.floor(M/2))
(fs,x)=wavfile.read('WebSDR.wav')
x1=x[5000:5000+M]*np.hamming(M)
N=511
fftbuffer=np.zeros([N])
fftbuffer[:hM1]=x1[hM2:]
fftbuffer[N-hM2:]=x1[:hM2]
X=fft(fftbuffer)
mX=abs(X)
pX=np.angle(X)
suptitle("Анализ радиосигналаWebSDR")
subplot(3, 1, 1)
st='Входной сигнал (WebSDR.wav)'
plot(x,linewidth=2, label=st)
legend(loc='center')
subplot(3, 1, 2)
st=' Частотный спектр входного сигнала'
plot(mX,linewidth=2, label=st)
legend(loc='best')
subplot(3, 1, 3)
st=' Фазовый спектр входного сигнала'
pX=np.unwrap(np.angle(X))
plot(pX,linewidth=2, label=st)
legend(loc='best')
show()
Для сравнительного анализа воспользуемся вейвлет скалограммой, которую можно построить с использованием функции tree = pywt.wavedec(signal, 'coif5') в matplotlib.
from pylab import *
import pywt
import scipy.io.wavfile as wavfile
# Найти наибольшую мощность двух каналов, которая меньше или равна входу.
def lepow2(x):
return int(2 ** floor(log2(x)))
#Скалограмма с учетом дерева MRA.
def scalogram(data):
bottom = 0
vmin = min(map(lambda x: min(abs(x)), data))
vmax = max(map(lambda x: max(abs(x)), data))
gca().set_autoscale_on(False)
for row in range(0, len(data)):
scale = 2.0 ** (row - len(data))
imshow(
array([abs(data[row])]),
interpolation = 'nearest',
vmin = vmin,
vmax = vmax,
extent = [0, 1, bottom, bottom + scale])
bottom += scale
# Загрузите сигнал, возьмите первый канал.
rate, signal = wavfile.read('WebSDR.wav')
signal = signal[0:lepow2(len(signal))]
tree = pywt.wavedec(signal, 'coif5')
gray()
scalogram(tree)
show()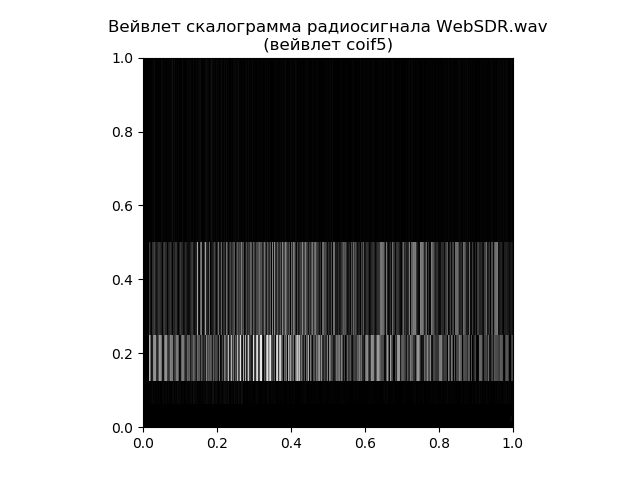
Таким образом, скалограмма дает более детальный ответ на вопрос о распределении частот во времени, а быстрое преобразование Фурье отвечает за сами значения частот. Всё зависит от поставленной задачи даже для такого простого примера.
Выводы
- Приведено обоснование использования дискретного вейвлет -преобразования для динамических сигналов.
- Приведены примеры вейвлет-анализа с использованием PyWavelets 1.0.3 — бесплатного программного обеспечение с открытым исходным кодом, выпущенного по лицензии MIT.
- Рассмотрены программные средства для практического использования библиотеки PyWavelets.
Комментарии (18)

geisha
13.05.2019 16:30Программные средства — это, конечно, замечательно, но неплохо бы в статье про вейвлеты иметь хотя бы одну формулу этого самого вейвлета. И уж совсем замечательно было бы научиться выдерживать отступы и подписывать оси в matplotlib.
Справедливости ради: Фурье-преобразование справляется с "нестационарными" сигналами посредством супер-нетривиального хака: берётся необходимый кусок сигнала и преобразуется. Преимущества над вейвлетами очевидны: никаких требований к памяти, фиксированная сложность и получение коэффициентов на лету.

Scorobey Автор
13.05.2019 16:52Формулы для материнских вейвлетов я приводил в статье Вейвлет-анализ основы. Повторяю для Вас:

Что касается «супер-нетривиального хака» поделитесь ссылкой ознакомлюсь. Спасибо за комментарий.
Colorbit
13.05.2019 19:54Под «супер-нетривиальным хаком» наверное понимается Оконное преобразование Фурье.

Scorobey Автор
13.05.2019 20:36Оконное Фурье преобразование не обладает свойствами масштабирования и задержки.

geisha
14.05.2019 11:28Я не совсем понимаю, почему вы так утверждаете: сам выбор окна обладает свойствами масштабирования (размер окна) и задержки (положение окна на временной шкале).

Scorobey Автор
14.05.2019 12:19При использовании оконного преобразования Фурье невозможно одновременно обеспечить хорошее разрешение по времени и по частоте. Чем уже окно, тем выше разрешение по времени и ниже разрешение по частоте.Разрешение по осям является постоянным. Это нежелательно для ряда задач, в которых информация по частотам распределена неравномерно. В таких задачах в качестве альтернативы оконному преобразованию Фурье может использоваться вейвлет-преобразование, временное разрешение которого увеличивается с частотой.

ValeriyS
13.05.2019 19:55Название статьи «Часть 1» и отсутствие ссылки на предыдущую вводную статью делает вопрос о формулах вполне резонным. Я на месте автора сразу бы добавил в свою статью отсутствующую ссылку вместо того, чтобы пенять на невнимательность (? — скорее слабое владение телепатией) спрашивающего.

Scorobey Автор
13.05.2019 20:32Из текста в начале статьи «При обработке данных на компьютере может выполняться дискретизированная версия непрерывного вейвлет-преобразования, основы которого описаны в моей предыдущей статье». Но ссылку уже добавил потому что «предыдущая статья» это не ссылка.Спасибо за замечание.

ValeriyS
13.05.2019 20:41Спасибо за позитивную реакцию. Давно присматриваюсь к вейвлет-преобразованиям, но пока что на самом деле в железе (FPGA) проще делать FFT после оконной функции на перекрывающихся участках входного сигнала. Прорывным для практического использования вейвлетов, которые выдают двумерную картинку, было бы последующее использование сверточных нейронных сетей, т.к. они наиболее проработаны для обработки двумерных входных данных — изображений.

Refridgerator
14.05.2019 12:03Справедливости ради: Фурье-преобразование справляется с «нестационарными» сигналами посредством супер-нетривиального хака: берётся необходимый кусок сигнала и преобразуется. Преимущества над вейвлетами очевидны: никаких требований к памяти, фиксированная сложность и получение коэффициентов на лету.
Справедливости ради: вейвлет-анализ придумали совсем не глупые люди и с Фурье-преобразованием, в том числе и оконным, совершенно точно хорошо знакомыми. И когда вам понадобится, к примеру, определить локальный максимум некоторой частоты во времени с максимально возможной точностью — то внезапно окажется, что использовать для этого SFFT с перекрытием в один семпл очень, очень накладно.

akhkmed
14.05.2019 00:13Спасибо за статью. Подскажите, какие есть применения у синтеза сигнала из вэйвлет-образа и любой ли вэйвлет позволяет делать обратное преобразование?

Refridgerator
14.05.2019 06:551) шумоподавление, нелинейная фильтрация
2) нет
akhkmed
14.05.2019 12:08Спасибо, подскажите, пожалуйста, что почитать об этом?

Refridgerator
14.05.2019 12:29Например. Хотя для начала не помешает разобраться в теории ЦОС (включая теорию функции комплексной переменной) достаточно для того, чтобы уметь самостоятельно синтезировать свои банки фильтров в логарифмической шкале частот. После этого все вопросы о вейвлетах отпадут сами собой.

cjmarse
16.05.2019 07:33Большое спасибо за статью и жду следующие части. Отдельное спасибо за примеры на python.
Попытаюсь применить вейвлеты для обработки геофизических данных.


Aoshi77
«Таким образом, скалограмма дает более детальный ответ на вопрос о распределении частот во времени, а быстрое преобразование Фурье отвечает за сами значения частот. Всё зависит от поставленной задачи даже для такого простого примера.»
А можно ли дать более развернутый ответ, так что же все таки показывает скалограмма, с чем эти показания можно связать, если на частотном спектре, мы явно видим выделенные частоты, то что мы видим здесь?
Спасибо!
Scorobey Автор
Допустим на масштабе а=1 сдвиг происходит на b=1. ( к примеру )
соответственно по ((t-b)/a) вейвлет помещается в точки на оси Х
((1-1)/1)=0
((2-1)/1)=1
((3-1)/1)=2…
Тогда на масштабе а=2 по формуле ((t-b)/a) получим сдвиг несколько меньше (ведь на 2 делим).
((1-1)/2)=0
((2-1)/2)=0.5
((3-1)/2)=1…
Т.е на том же временном интервале шагов анализа больше!