Методы Ньютона-Котеса — это совокупность техник приближенного интегрирования, основанных на:
В этой статье будут рассмотрены несколько методов Ньютона-Котеса:
Метод трапеций — простейший из рассмотренных. В качестве примера возьмем следующий интеграл:
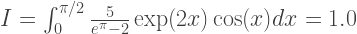
Точность приближения зависит от числа N отрезков, на которые разбивается промежуток интегрирования. Таким образом, длина промежутка:
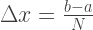
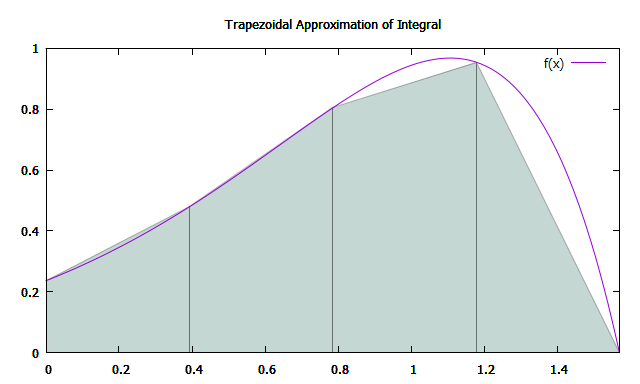
Площадь трапеции может быть вычислена по формуле:
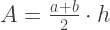
Суммируя все вышесказанное, приближенное значение интеграла вычисляется по формуле:
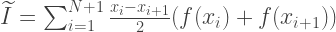
Функция, вычисляющая интеграл методом трапеций должна принимать 4 параметра:
Метод Симпсона заключается в интегрировании интерполяционного многочлена второй степени функции f(x) с узлами интерполяции a, b и m = (a+b)/2 — параболы p(x).Для повышения точности имеет смысл разбить отрезок интегрирования на N равных промежутков(по аналогии с методом трапеций), на каждом из которых применить метод Симпсона.
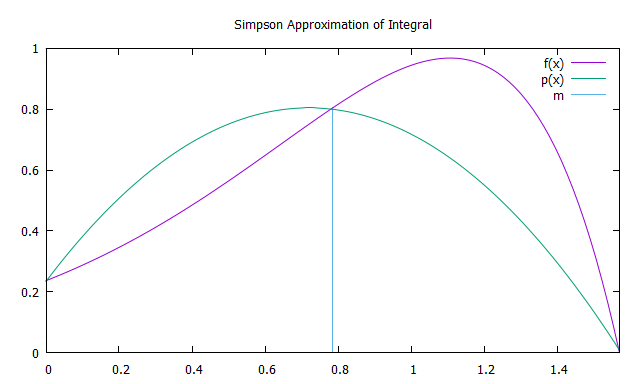
Площадь параболы может быть найдена суммированием площадей 6 прямоугольников равной ширины. Высота первого из них должна быть равна f(a), с третьего по пятый — f(m), шестого — f(m). Таким образом, приближение методом Симпсона находим по формуле:
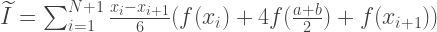
Пусть T(x) — приближение интеграла, полученное методом трапеций с шагом x. Получим 3 таких приближения, уменьшая размер шага в 2 раза при каждом вычислении.

Построим теперь симметричную относительно оси y параболу, проходящую через точки T(1) и T(1/2) чтоб экстраполировать полученные значения для x стремящегося к 0.
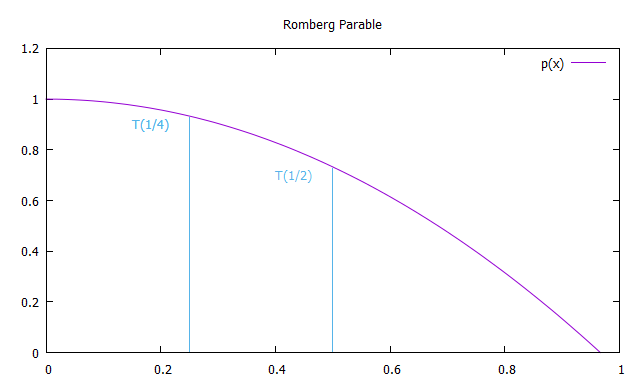
Следовательно, каждый член первого столбца R(n, 0) приближений Ромберга эквивалентен решениям полученным методом трапеций, а каждое решение второго столбца R (n, 1) — методом Симпсона. Таким образом, формулы для приближенного интегрирования методом Ромберга:
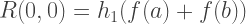
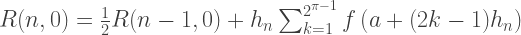
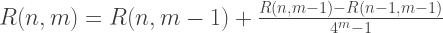
Реализация на C++:
- разбиении отрезка интегрирования на равные промежутки;
- аппроксимации подинтегральной функции на выбранных промежутках многочленами;
- нахождении суммарной площади полученных криволинейных трапеций.
В этой статье будут рассмотрены несколько методов Ньютона-Котеса:
- метод трапеций;
- метод Симпсона;
- метод Ромберга.
Метод трапеций
Метод трапеций — простейший из рассмотренных. В качестве примера возьмем следующий интеграл:
Точность приближения зависит от числа N отрезков, на которые разбивается промежуток интегрирования. Таким образом, длина промежутка:

Площадь трапеции может быть вычислена по формуле:
Суммируя все вышесказанное, приближенное значение интеграла вычисляется по формуле:
Функция, вычисляющая интеграл методом трапеций должна принимать 4 параметра:
- границы отрезка интегрирования;
- подинтегральную функцию;
- число N промежутков разбиения.
double trapezoidalIntegral(double a, double b, int n, const std::function<double (double)> &f) {
const double width = (b-a)/n;
double trapezoidal_integral = 0;
for(int step = 0; step < n; step++) {
const double x1 = a + step*width;
const double x2 = a + (step+1)*width;
trapezoidal_integral += 0.5*(x2-x1)*(f(x1) + f(x2));
}
return trapezoidal_integral;
}Метод Симпсона
Метод Симпсона заключается в интегрировании интерполяционного многочлена второй степени функции f(x) с узлами интерполяции a, b и m = (a+b)/2 — параболы p(x).Для повышения точности имеет смысл разбить отрезок интегрирования на N равных промежутков(по аналогии с методом трапеций), на каждом из которых применить метод Симпсона.

Площадь параболы может быть найдена суммированием площадей 6 прямоугольников равной ширины. Высота первого из них должна быть равна f(a), с третьего по пятый — f(m), шестого — f(m). Таким образом, приближение методом Симпсона находим по формуле:
double simpsonIntegral(double a, double b, int n, const std::function<double (double)> &f) {
const double width = (b-a)/n;
double simpson_integral = 0;
for(int step = 0; step < n; step++) {
const double x1 = a + step*width;
const double x2 = a + (step+1)*width;
simpson_integral += (x2-x1)/6.0*(f(x1) + 4.0*f(0.5*(x1+x2)) + f(x2));
}
return simpson_integral;
}Метод Ромберга
Пусть T(x) — приближение интеграла, полученное методом трапеций с шагом x. Получим 3 таких приближения, уменьшая размер шага в 2 раза при каждом вычислении.
Построим теперь симметричную относительно оси y параболу, проходящую через точки T(1) и T(1/2) чтоб экстраполировать полученные значения для x стремящегося к 0.

Следовательно, каждый член первого столбца R(n, 0) приближений Ромберга эквивалентен решениям полученным методом трапеций, а каждое решение второго столбца R (n, 1) — методом Симпсона. Таким образом, формулы для приближенного интегрирования методом Ромберга:
Реализация на C++:
std::vector<std::vector<double>> rombergIntegral(double a, double b, size_t n, const std::function<double (double)> &f) {
std::vector<std::vector<double>> romberg_integral(n, std::vector<double>(n));
romberg_integral.front().front() = trapezoidalIntegral(a, b, 1, f);
double h = b-a;
for(size_t step = 1; step < n; step++) {
h *= 0.5;
double trapezoidal_integration = 0;
size_t stepEnd = pow(2, step - 1);
for(size_t tzStep = 1; tzStep <= stepEnd; tzStep++) {
const double deltaX = (2*tzStep - 1)*h;
trapezoidal_integration += f(a + deltaX);
}
romberg_integral[step].front() = 0.5*romberg_integral[step - 1].front() + trapezoidal_integration*h;
for(size_t rbStep = 1; rbStep <= step; rbStep++) {
const double k = pow(4, rbStep);
romberg_integral[step][rbStep] = (k*romberg_integral[step][rbStep-1] - romberg_integral[step-1][rbStep-1])/(k-1);
}
}
return romberg_integral;
}

OldFisher
Девчонки и мальчишки, а также их родители! Пожалуйста, помните, что в реальной жизни
std::functionнадо передавать по значению, векторы — по ссылке, а для организации двумерных массивов есть более эффективные средства, чем вектор векторов.wilcot
Если вы говорите про более эффективные средства, то хотя бы их перечисляйте. А пока это выглядит как попытка поумничать.
Sazonov
Вам в реальности не нужно будет в рантайме менять длины некоторых строк/столбцов. Самое простое, но намного более эффективное решение это std::array из std::array. Никаких лишних аллокаций, всё в памяти одним блоком.
DistortNeo
Ну а динамических многомерных массивов в стандартной библиотеке C++, к сожалению, до сих пор нет.
Sazonov
Мне очень сложно представить ситуацию, когда они бы понадобились на практике. А если и понадобятся в узкоспецифическом проекте, то их не очень сложно реализовать самому.
wilcot
Изменять в рантайме размеры может и не нужно, но выделять, к примеру, матрицу размера, определённого в compile time, выглядит не всегда разумно. Вообще, как мне кажется, не нужно делать преждевременные оптимизации в ущерб читаемости кода, так как может оказаться, что проседания производительности не в лишних аллокациях. Да не спорю, круто писать сразу оптимальный во всех смыслах код, но кажется, что это может оказаться сильно дороже, чем хотелось бы.
OldFisher
Дать исчерпывающее перечисление всё равно не получится. Это может быть простой одномерный вектор вкупе с ручным вычислением эффективного индекса,
std::array, самописный класс, обёртка над стандартным контейнером, что-то из контейнеров Boost и многое другое. И выбор зависит от немалого количества факторов. Применительно к данной статье мог бы подойти «голый» одномерный вектор или самописная обёртка, хотя первое несколько усложнит код по сравнению с «идеальным» двумерным массивом (вектор векторов в этом смысле тоже не подарочек), а второе потребует как минимум привести интерфейс и пояснения.DistortNeo
Когда речь заходит об оптимизации вычислений, то передавать вообще надо не std::function, а шаблонный функтор. Ну и алгоритмические моменты: нет никакого смысла вычислять значение функции в одной и той же точке дважды.
OldFisher
По алгоритмическим моментам поддержу. И повторные вычисления желательно сокращать, и возведение в квадрат и четвёртую степень лучше делать через умножение, а не дорогостоящий
pow.А вот накладные расходы на вызов
std::functionбудут заметны на общем фоне только для совсем уж простых вычислений. Стоит ли жертвовать ради этого выразительностью и универсальностью, которые даётfunction? Зависит от обстоятельств, но в учебном проекте вряд ли стоит сражаться за считанные такты ценой снижения ясности кода.