Вирусы и питоны
Всё, что один человек написал, другой может переврать!
В прессе масса информации про разные вирусы — страшилки, наив, бесстрашие с безумием и откровенные роботексты, но проверить ничего из этого нельзя. Поэтому решил проверить сам как и какие параметры влияют на состояние, развитие и деградацию связной структуры и сделать выводы.
Перейдем к делу, у нас есть узлы(может это и люди) связанные между собой. Узлы деградируют/болеют и их можно лечить, изолировать в карантине, ну и они отключаются, увы иногда навсегда.
# число узлов/жителей
w_size = 1024 * 32
# связность, пытаемся создать у каждого узла не более max_conn связей
max_conn = 6
# вероятность деградации узла, заражения здорового, появления вируса и т.д.
# за один тик времени при общении с зараженным узлом вне карантина
infection_probably = 0.9
# вероятность починки узла, выздоровления больного,
# исчезновения вируса и т.д. за один тик времени
pr_recover = 0.75
# количество тиков времени до попадания в карантин.
# Или до выпадения из структуры компрометированного узла
# т.е. узел скомпрометирован/болен, но это еще не обнаружено и он несколько тиков
# времени продолжает заражать других
quarantine = 5
# если после стольких дней узел не исправлен - удаляем окончательно
dead = 14
import numpy as np
from tqdm import tqdm
import matplotlib
import matplotlib.pyplot as plt
from termcolor import colored
l_immun = []
l_quar = []
l_died =[]
l_infl = []
map_conn = []
# храним тут состояние узла. =0 исправен, >0 но <quarantine то заразен
# и не изоливан, >quarantine то изолирован, >dead - отключен
# <0 - вылечен и обладает иммунитетом/патч применен
map_stat = np.zeros((w_size), dtype="int16")
# храним связную структуру в виде списа списков связности.
# Т.е. map_conn[i] - список с номерами узлов связанных с узлом i
for i in range(w_size):
map_conn.append([])
for i in tqdm(range(w_size)):
t = np.random.randint(0, max_conn//2)
tt = np.random.randint(0, w_size, (t))
for j in tt:
map_conn[i].append(j)
map_conn[j].append(i)
for i in range(w_size):
map_conn[i] = list(set(map_conn[i]))
# очевидно, что возможно и больше max_conn связей.
# Мы создаем случайно для каждого узла max_conn//2 связей,
# но связность симметрична.
# состояние узла. Если 0 то здоров, если <0 переболел, восстановлен и
# не будет больше болеть
# если >0 то инфицирован/деградирует, если >quarantine, то в изоляции
# если >dead отключен окончательно, увы.
map_stat[:] = 0
# в начале все здоровы
map_stat[np.random.randint(1, w_size)] = 1
# случайный узел деградировал, первый день деградации.
day = 1
while True:
tmp_map_conn = map_conn.copy()
tmp_map_stat = map_stat.copy()
# тут сохраняем структуру во временное хранилище и
# начнем вычислять новое состояние
for i in range(w_size):
# если узел был инфицирован и восстановлен, Болел - выздоровел - иммунитет
if tmp_map_stat[i] < 0:
map_stat[i] = tmp_map_stat[i]
continue
# если узел был инфицирован и более чем quarantine тиков времни/дней
# увеличиваем счетчик тиков на 1
if tmp_map_stat[i] >= quarantine:
map_stat[i] = tmp_map_stat[i] + 1
continue
# если узел был инфицирован и менее чем quarantine тиков времни/дней
# то он выздоравливает с вероятностью pr_recover
# или счетчик тиков деградации увеличивается на один
if tmp_map_stat[i] > 0:
if np.random.rand() < pr_recover:
map_stat[i] = -tmp_map_stat[i]
else:
map_stat[i] = tmp_map_stat[i] + 1
# если узел в деградации больше quarantine тиков,
# то наверно это обнаружится и узел изолируют и начнут восстанавливать
# и все его связи исчезнут и связи с ним тоже
if map_stat[i] >= quarantine:
for j in tmp_map_conn[i]:
if i in map_conn[j]:
map_conn[j].remove(i)
map_conn[i] = []
continue
# если узел здоров, то в общении со своим контактом может
# заразиться с вероятностью infection_probably
if tmp_map_stat[i] == 0:
map_stat[i] = 0
for j in tmp_map_conn[i]:
t = np.random.rand()
if (
t < infection_probably
and tmp_map_stat[j] > 0
and tmp_map_stat[j] < quarantine
):
map_stat[i] = 1
break
# считаем число элементов до 0, от 0 до quarantine
# от quarantine до dead
immun = np.count_nonzero(map_stat < 0)
quar = np.count_nonzero((map_stat >= quarantine) & (map_stat < dead))
died = np.count_nonzero(map_stat >= dead)
infl = np.sum((map_stat > 0) & (map_stat < dead))
print(
"day {0:3d} infected {1:6d} recovered {2:6d} quarantine {3:6d} died {4:6d}".format(
day, infl, immun, quar, died
)
)
l_immun.append(immun)
l_quar.append(quar)
l_died.append(died)
l_infl.append(infl)
# если больных нет, считать прекращаем
if infl == 0:
break
# и так далее
day += 1
print ("\n{:6d} point number ".format(w_size))
print ("{:4d} maximum number of links ".format(max_conn))
print ("{:3.2f} the probability of infection in a single contact ".format(infection_probably))
print ("{:3.2f} chance to recover in one day ".format(pr_recover))
print ("{:4d} the number of days before the detection of the disease and the beginning of quarantine".format(quarantine))
print ("{:4d} number of treatment days to death".format(dead))
t = np.arange(0, day, 1.)
print (colored("the number of recovered ", "red"))
print (colored("the number in quarantine ", "green"))
print ("the number of died ")
print (colored("the number of infected ", "blue"))
fig, ax = plt.subplots()
ax.plot(t, l_immun, color='red')
ax.plot(t, l_quar, color='green')
ax.plot(t, l_died, color='black')
ax.plot(t, l_infl, color='blue')
ax.set(xlabel='time (days)', ylabel='number',
title='virus behavior')
ax.grid()
fig.savefig("test.png")
plt.show()
Тут самое время сказать — ну и что, что такого могут открыть десяток строк питона!
Мне же результат был интересен и полезен.
day 1 infected 2 recovered 1 quarantine 0 died 0
day 2 infected 4 recovered 2 quarantine 0 died 0
day 3 infected 10 recovered 4 quarantine 0 died 0
day 4 infected 12 recovered 9 quarantine 0 died 0
day 5 infected 11 recovered 20 quarantine 0 died 0
day 6 infected 21 recovered 28 quarantine 0 died 0
day 7 infected 39 recovered 43 quarantine 0 died 0
day 8 infected 66 recovered 72 quarantine 0 died 0
day 9 infected 92 recovered 120 quarantine 0 died 0
day 10 infected 127 recovered 197 quarantine 0 died 0
day 11 infected 211 recovered 292 quarantine 1 died 0
day 12 infected 352 recovered 446 quarantine 1 died 0
day 13 infected 578 recovered 714 quarantine 1 died 0
day 14 infected 949 recovered 1151 quarantine 1 died 0
day 15 infected 1492 recovered 1841 quarantine 1 died 0
day 16 infected 2192 recovered 2954 quarantine 2 died 0
day 17 infected 3045 recovered 4612 quarantine 3 died 0
day 18 infected 3995 recovered 6902 quarantine 8 died 0
day 19 infected 4617 recovered 9889 quarantine 14 died 0
day 20 infected 4595 recovered 13385 quarantine 16 died 1
day 21 infected 3880 recovered 16847 quarantine 26 died 1
day 22 infected 2887 recovered 19722 quarantine 41 died 1
day 23 infected 1834 recovered 21859 quarantine 58 died 1
day 24 infected 1106 recovered 23203 quarantine 67 died 1
day 25 infected 688 recovered 23977 quarantine 75 died 2
day 26 infected 412 recovered 24422 quarantine 85 died 3
day 27 infected 249 recovered 24679 quarantine 83 died 8
day 28 infected 174 recovered 24796 quarantine 80 died 14
day 29 infected 112 recovered 24873 quarantine 81 died 17
day 30 infected 86 recovered 24894 quarantine 71 died 27
day 31 infected 60 recovered 24906 quarantine 58 died 42
day 32 infected 42 recovered 24908 quarantine 41 died 59
day 33 infected 33 recovered 24909 quarantine 32 died 68
day 34 infected 23 recovered 24910 quarantine 23 died 77
day 35 infected 12 recovered 24910 quarantine 12 died 88
day 36 infected 9 recovered 24910 quarantine 9 died 91
day 37 infected 6 recovered 24910 quarantine 6 died 94
day 38 infected 2 recovered 24910 quarantine 2 died 98
day 39 infected 2 recovered 24910 quarantine 2 died 98
day 40 infected 0 recovered 24910 quarantine 0 died 100
32768 point number
6 maximum number of links
0.90 the probability of infection in a single contact
0.75 chance to recover in one day
5 the number of days before the detection of the disease and the beginning of quarantine
14 number of treatment days to death
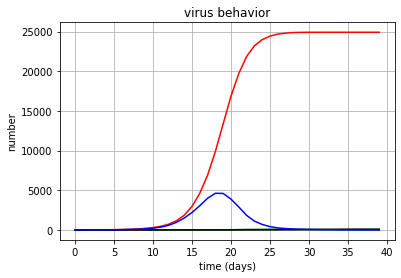
Получилось вот что (и был бы рад, если кто проверит и ткнет в ошибку): при infection_probably = 0.9 и max_conn = 6, т.е. при страшной заразности и при минимуме общения — 6 контактов в день — массовой деградации нет. Десяток запусков конечно не статистика, но мне достаточно.
А вот при infection_probably = 0.1 и max_conn = 40 погибает половина. Т.е. слабозаразная напасть при большой связности сообщества губит половину её членов. Причем от величины quarantine это не зависит.


ChePeter Автор
Всего голосов 15: ^ 1 и v 14
Причины минусов
Низкий технический уровень материала — 42.86%
Больше рекламы, чем пользы — 0%
Не соответствует тематике Хабра — 7.14%
В тексте много ошибок и опечаток — 0%
Пост небрежно оформлен — 7.14%
Личная неприязнь к автору или компании — 0%
В статье нет новой для меня информации — 0%
Ничего не понял после прочтения — 42.86%
Другое — 0%
Sirion
Почему вы решили оставить этот комментарий?