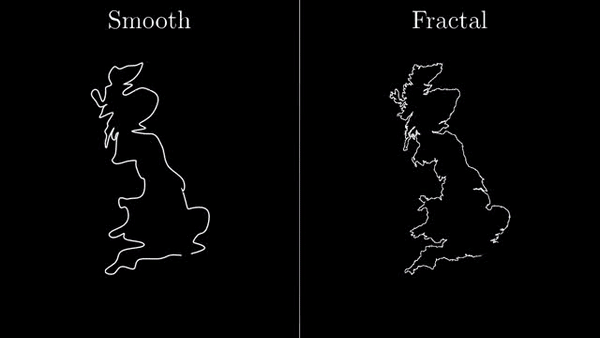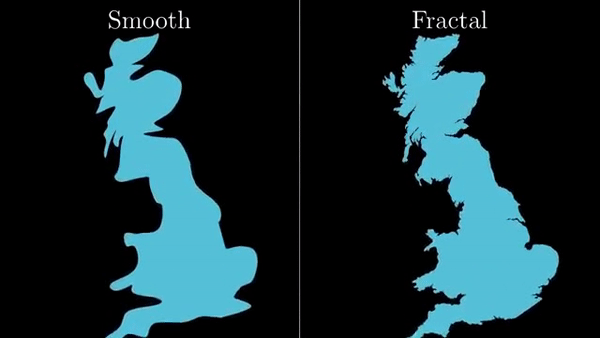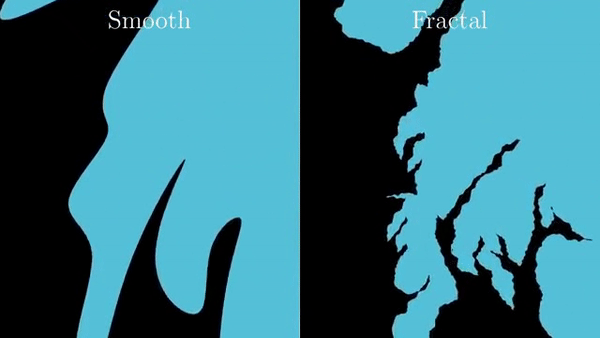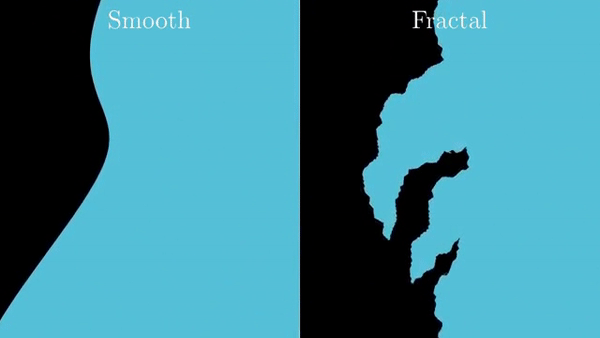
Фракталы — это самоподобные штуковины. Не совсем так.
Идея Мандельброта была шире. Как моделировать природу с учетом неровностей? В некотором роде, фрактальная геометрия — это бунт против классического матанализа, основная идея которого, что все будет очень гладким, если достаточно увеличить. Мандельброту это показалось чересчур идеальным, бесполезно абстрактным.
Настоящая идея фрактала имеет отношение к дробной размерности.
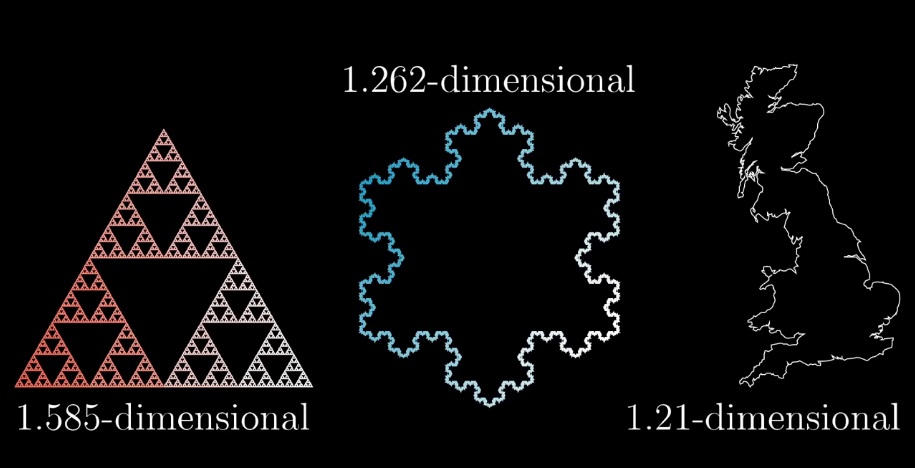
Дробная размерность
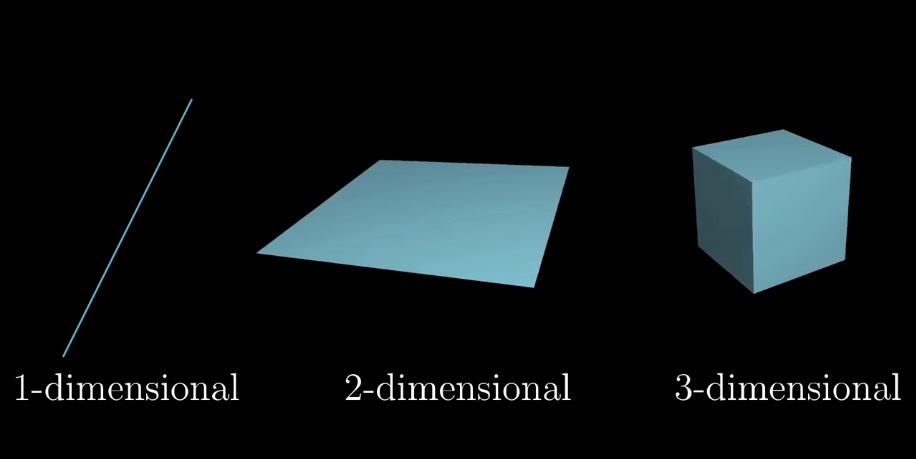
Многим кажется, что размерность имеет смысл только для натуральных чисел.

Рассмотрим 4 самоподобные фигуры:
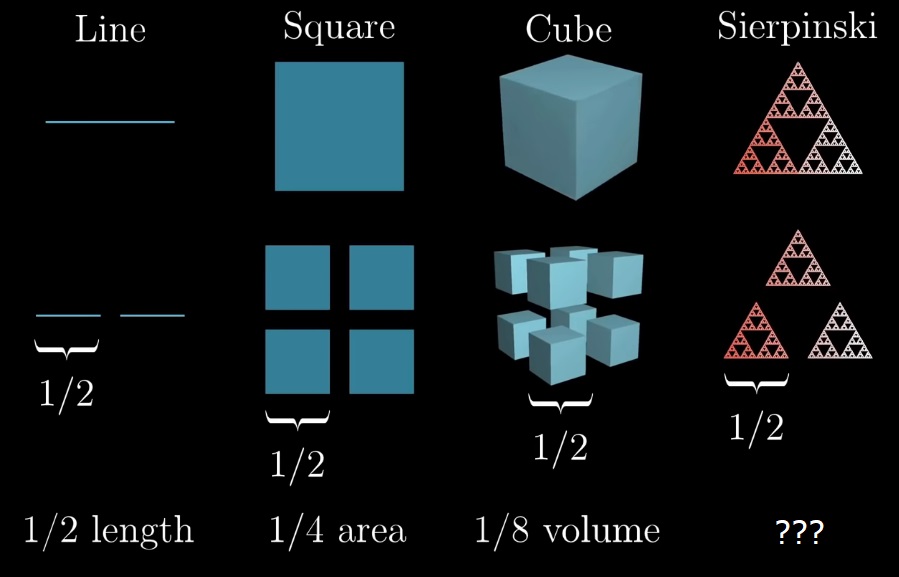
Составная часть каждой фигуры является точной копией целого.
Какое слово обобщает идею длины, площади и объема? Обычно используется слово «мера» (measure), но для наглядности можно говорить о «массе». Представим, что все упомянутые фигуры сделаны из металла. Фрактальная размерность связана с тем, как меняется масса фигур, когда вы их масштабируете.
Самоподобные фигуры дает четкое понимание того, как сравнивать «массы».
Когда вы уменьшаете масштаб отрезока в 2 раза, «масса» уменьшается в 2 раза (21).
Когда вы уменьшаете масштаб квадрата в 2 раза, масса уменьшается в 4 раза (22).
Уменьшая масштаб куба в 2 раза, масса уменьшается в 8 раз (23).
Для треугольника Серпинского при уменьшении масштаба в 2 раза очевидно, что масса уменьшается в 3 раза (2?):
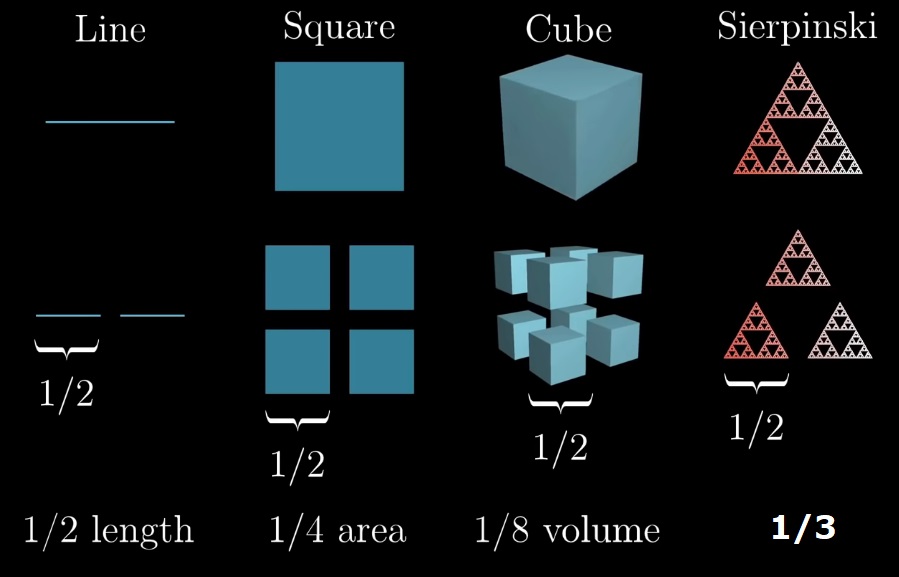
Тогда размерность треугольника Серпинского = log2(3) ? 1,585
«Длина» и «площадь» для треугольника Серпинского не совсем подходящие параметры. «Длина» треугольника Серпинского = ?, «площадь» = 0. Нам нужен 1,585 мерный аналог длины(площади).
Кривая фон Коха состоит из 4 собственных копий:
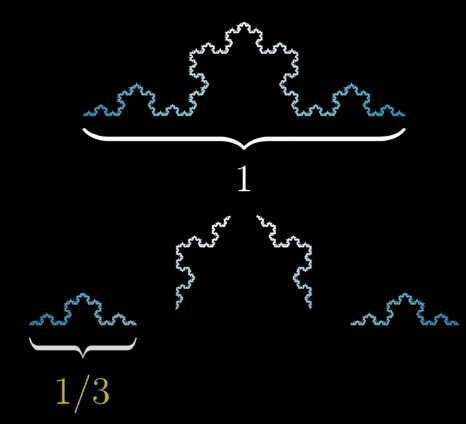
Когда масштаб уменьшается в 3 раза, «масса» уменьшается в 4 раза. Тогда размерность кривой фон Коха = log3(4) ? 1,262
Следующая фигура состоит из 8 своих копий:

Уменьшая масштаб в 4 раза, «масса» уменьшится в 8 раз. Размерность = log4(8) ? 1,5

«Масса» подходит только для самоподобных фигур. Но это слишком ограничено. Большинство двумерных фигур не самоподобны.
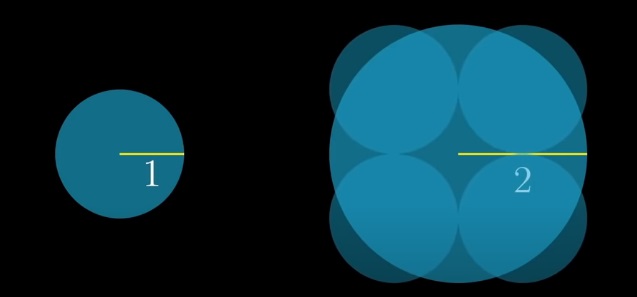
«Масса» круга при уменьшении масштаба уменьшается в 4 раза. Но мы никак не можем составить из 4 маленьких кругов один большой.
Можно использовать метод сетки:
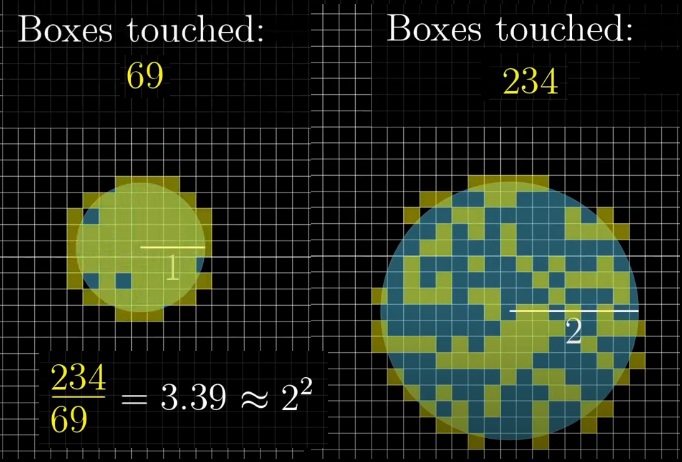
Если взять зерно сетки поменьше, получим более точный результат:

Увеличение количества затронутых клеточек идет как вторая степень от увеличения масштаба.
Для треугольника Серпинского:
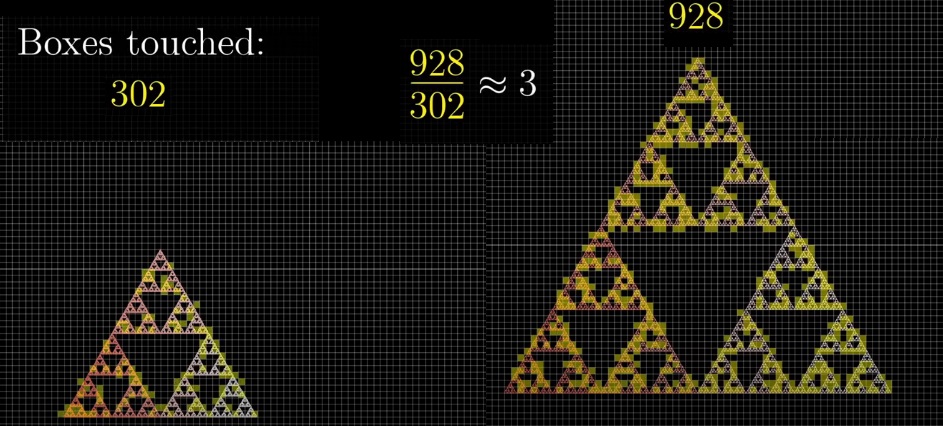
Увеличение количества затронутых клеточек идет как как степень 1,585 от увеличения масштаба.
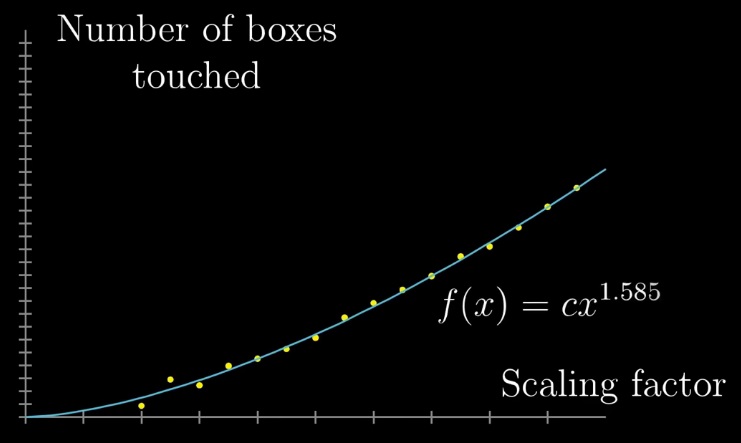
Для береговой линии:
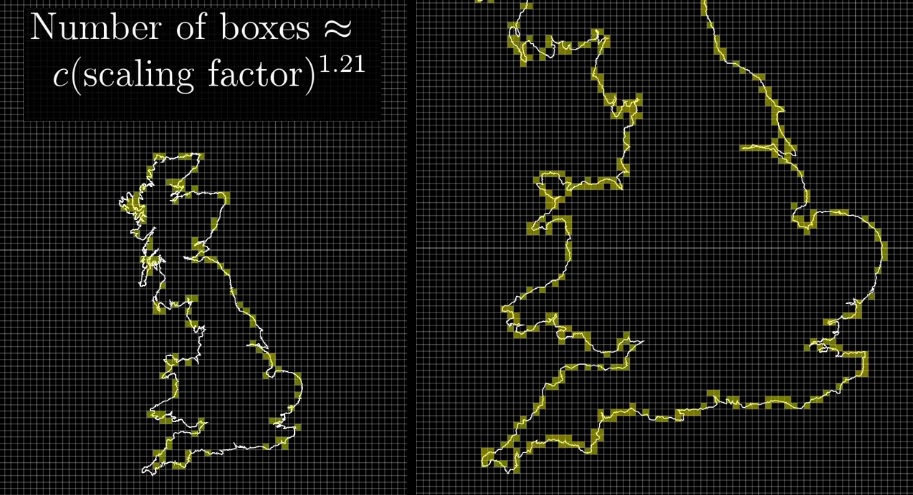
Увеличение количества затронутых клеточек идет как как степень 1,21 от увеличения масштаба.

При переходе к логарифмической шкале, график будет стремиться к прямой, и важен угол ее наклона, но не для всех фигур это будет прямая с постоянным углом наклона.
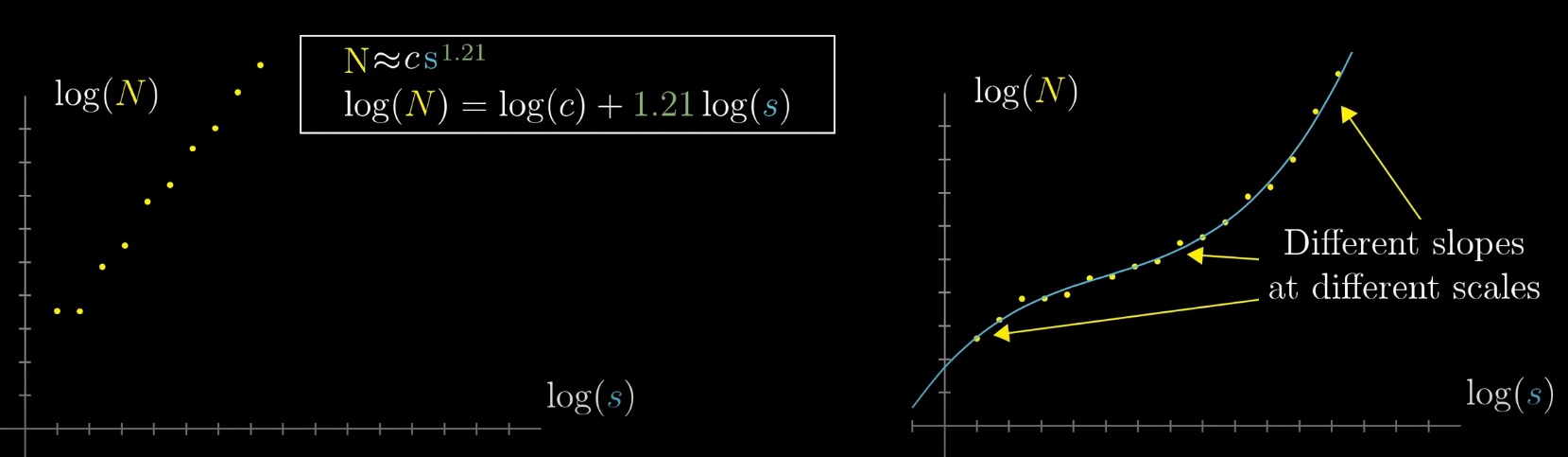
Различные точки на графике и усредненная прямая, которая им соответствует- это эмпирическое значение размерности.
Итак, фракталы — это фигуры, размерность которых — не целое число. У нас есть качественный способ сказать, что фигура неровная и будет оставаться неровной, если её увеличить.
В трехмерном пространстве мы считаем пересечение с трёхмерной сеткой кубиков.

Когда фигура меньше кубиков, мы воспринимаем её как линию, одномерную. Количество кубиков, которые она пересекает пропорционально её длине (первая степень).
При увеличении у нас получается труба (двумерная), которая пересекает своей поверхностью кубики сетки. И количество кубиков пропорционально второй степени.
Если мы еще увеличим масштаб, фигура выглядит одномерной. Количество кубиков будет пропорционально первой степени.
Процесс присвоения размерности фигуре может быть не очевидным и оставляет простор для разных соглашений и определений.
- Minkowski–Bouligand dimension
- Information dimension
- Hausdorff dimension
- Packing dimension
- Correlation dimension
- Generalized or Renyi dimensions
- Higuchi dimension
- Lyapunov dimension
- Assouad dimension
- Local connected dimension

В теории увеличение масштаба может быть бесконечным, на практике достаточно просто большого разброса масштабов для построения графика. Главное, чтобы размерность оставалась приблизительно постоянной на разных масштабах.
Береговая линия Британии имеет размерность 1,21 на различных масштабах. Размерность береговой линии Норвегии имеет размерность 1,52, что есть численный способ сказать о том, что она более неровная.
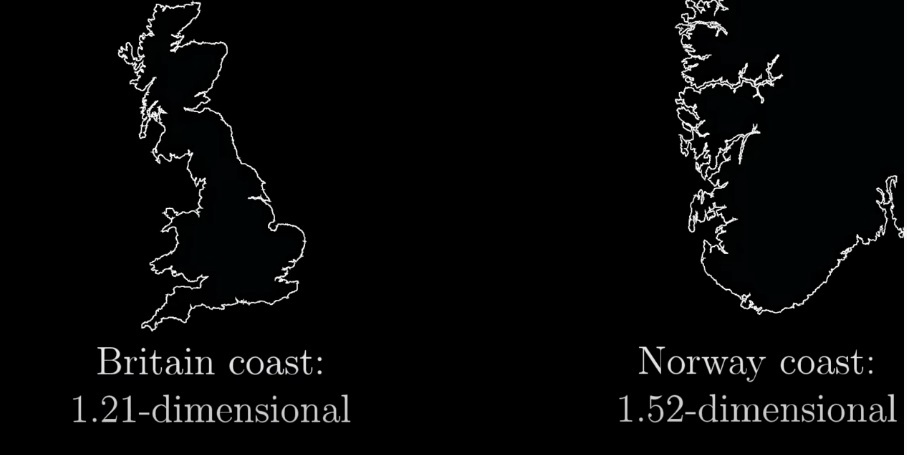
Фрактальная размерность — один из факторов, что объект природного происхождения, а не создан человеком.
Оригинал видео
Русский дубляж


lz961
аппроксимировать обычную, непрерывно-дифференцируемую кривую линию цепочкой квадратов, казалось бы не очень хорошая идея. Так можно дойти до аппроксимации кривой ломаной, участки которой параллельны какому либо из координатных ортов, «лесенкой». В этом случае можно «доказать» равенство длины гипотенузы сумме катетов.
mayorovp
Тут "спасает" тот факт, что с помощью подобной аппроксимации не пытаются измерять длину.
sergeperovsky
И подобная геометрия существует. И весьма полезна для некоторых задач.
Простейший пример — поездки по городу. «Расстояние», это сумма отрезков дорог. И «гипотенуза» может оказаться не короче «катетов».