27.01.2021 09:20
miksaz 2 649 Источник

Всем привет! В этом посте я расскажу, как наша команда участвовала и заняла третье место в Black-Box Optimization Challenge — соревновании по автоматическому подбору параметров для моделей машинного обучения. Особенность соревнования в том, что алгоритм не знает, какая модель машинного обучения используется, какую задачу она решает, и за что отвечает каждый из оптимизируемых параметров.


Звучит как соревнование, в котором лучше случайного поиска ничего не придумаешь, но существует целый класс алгоритмов для таких задач, о которых мы и поговорим под катом.



Меня зовут Никита Сазанович, я учусь на 2-м курсе магистратуры «Программирование и анализ данных» в Питерской Вышке. На протяжении трех месяцев мы с командой из JetBrains Research участвовали в соревновании по Black-Box Optimization (BBO) и заняли в нем третье место. Команда состояла из меня, Юрия Белоусова и Анастасии Никольской, которые тоже учатся в магистратуре, и руководителя нашей лаборатории Алексея Шпильмана. Наше решение строит разбиение пространства параметров и оптимизирует какой-то его участок, используя байесовскую оптимизацию. Про соревнование, наше решение и смежные понятия мы и поговорим в статье.


Что такое BBO


С понятием black box, вероятно, встречался каждый разработчик или в контексте black box тестирования, или программного обеспечения с закрытым исходным кодом, или чего-то еще. Все эти моменты объединяет то, что в абстракции black box наблюдаются только входные и выходные данные, а само устройство системы представляет собой «черный ящик»:



Например, при black box тестировании, тесты, как правило, пишутся теми, кто не принимал участия в написании тестируемого кода и не знает его устройства. Эти тестировщики руководствуются общими принципами тестирования функциональности программы (граничные случаи для входа, разбиение всех тестовых случаев на категории) без каких-либо предположений о том, как эта программа может быть реализована.


По аналогии, black box оптимизация должна оптимизировать какую-то модель, или в общем случае функцию $f$, у которой есть несколько входов $x_1, x_2, ..., x_n$, и есть возможность наблюдать выходной результат. Что за модель, для какой задачи мы наблюдаем результат, и что представляют из себя абстрактные параметры $x_i$, мы не знаем. К примеру, для линейной регрессии $y$ по $x$ мы можем определить два параметра: наклон $k$ и сдвиг $b$. А в качестве функции $f$ будем считать среднеквадратическую ошибку на нашем датасете $\{x_i, y_i\}$ в предположении того, что модель выглядит как $y=kx+b$. Тогда, зная, что у модели есть два вещественных параметра, алгоритм BBO оптимизации должен подобрать оптимальные наклон и сдвиг на нашем датасете.


Конечно, линейная регрессия имеет оптимальное решение в закрытой форме, и оптимизацию таким способом нам проводить не обязательно. Кроме того, даже если мы решили оптимизировать параметры линейной регрессии, а не найти их в закрытой форме, почему бы нам не использовать градиенты среднеквадратической ошибки? И это разумный вопрос, потому что если у нас есть возможность найти градиенты для каждого параметра, мы можем проводить оптимизацию классическими методами. Поэтому BBO в основном применяется в случаях, когда нет возможности посчитать градиент функции потерь по параметрам. Обычно такими параметрами являются гиперпараметры алгоритмов машинного обучения. Например, для метода k-ближайших соседей гиперпараметрами являются количество рассматриваемых соседей $n_{neighbors}$ и степень расстояния $p$, которое используется для определения близости.


Соревнование по BBO


Разобравшись в том, зачем и что собой представляет BBO, давайте поговорим про соревнование. Black-Box Optimization Challenge был организован разработчиками таких компаний, как Twitter, SigOpt, Valohai, Facebook, и проходил в рамках конференции NeurIPS 2020. Вся информация про соревнование расположена по адресу: https://bbochallenge.com.


Постановка задачи была следующая. Проверяющий код загадывает какую-то модель машинного обучения, выбирает датасет и метрику, с помощью которой он будет оценивать наборы гиперпараметров. Для однообразности, в случае если большее значение метрики соответствует лучшему результату (к примеру, метрика точности), проверяющий код будет возвращать отрицание ее значения, чтобы задача всегда заключалась в минимизации. Вашему алгоритму на старте передается информация о количестве параметров и ограничения на каждый из них вида $x_1$ — это вещественное число в диапазоне [0.01, 100], $x_2$ — это целое число в диапазоне [1, 4], а $x_3$ принимает категориальные значения из набора ['linear', 'poly', 'rbf', 'sigmoid']. Eсли провести обучение загаданной модели на выбранном датасете с предлагаемыми вами параметрами, ваш алгоритм должен предлагать какие-то наборы этих параметров, на которые проверяющий код будет возвращать значения метрики,. Более того, ваш алгоритм должен предлагать не один, а восемь наборов в каждой итерации, после чего он получает результаты. И количество таких итераций (загадал -> получил результаты -> ...) ограничено 16. То есть всего ваш алгоритм может предложить 128 конфигураций. Проверяющий код выставляет вам оценку в зависимости от того, насколько вам удалось уменьшить значение метрики одним из предложенных наборов.


Для лучшего понимания давайте посмотрим, как такое взаимодействие происходит для решения на задаче оптимизации точности классификации рукописных цифр (описание датасета) деревом принятия решений. У дерева принятия решений выделено шесть параметров, которые описаны в классе sklearn DecisionTreeClassifier:


  • $max\_depth$ означает максимальную глубину дерева (целое число от 1 до 15);
  • $min\_samples\_split $ означает минимальное число в процентах от всех сэмплов для того, чтобы дальше рассматривать разбиения этой вершины (вещественное число от 0.01 до 0.99);
  • $min\_samples\_leaf $ означает минимальное число в процентах от всех сэмплов, которое должно быть в любом листе (вещественное число от 0.01 до 0.49);
  • $min\_weight\_fraction\_leaf $ означает минимальный вес, который должен находиться в любом из листьев (вещественное число от 0.01 до 0.49);
  • $max\_features $ означает максимальный процент от всего числа признаков, которые мы будем рассматривать для одного разбиения (вещественное число от 0.01 до 0.99);
  • $min\_impurity\_decrease $ стоит за минимальным уменьшением impurity (число, использующееся для выбора разбиений) в нашем дереве (вещественное число от 0.0 до 0.5).

Рассмотрим некоторые итерации взаимодействия (все вещественные числа представлены с точностью до 3 цифр после запятой):


  • в __init__ алгоритм получает информацию о 6 параметрах, их типах и диапазонах значений;
  • в первом suggest алгоритм предлагает наборы (значения для параметров в порядке представления выше)
    [5, 0.112, 0.011, 0.010, 0.204, 0.250],
    [13, 0.144, 0.052, 0.017, 0.011, 0.362],
    [4, 0.046, 0.077, 0.013, 0.079, 0.075],
    [8, 0.014, 0.204, 0.072, 0.036, 0.237],
    [9, 0.985, 0.065, 0.067, 0.015, 0.122],
    [13, 0.379, 0.142, 0.266, 0.097, 0.313],
    [15, 0.015, 0.088, 0.142, 0.143, 0.438],
    [14, 0.461, 0.020, 0.030, 0.613, 0.204];
  • в первом вызове observe получает результаты
    [-0.107, -0.107, -0.107, -0.107, -0.107, -0.107, -0.107, -0.107];
  • в последнем suggest алгоритм предлагает наборы
    [9, 0.066, 0.013, 0.031, 0.915, 0.000],
    [8, 0.024, 0.012, 0.019, 0.909, 0.010],
    [9, 0.185, 0.020, 0.025, 0.925, 0.005],
    [15, 0.322, 0.014, 0.024, 0.962, 0.001],
    [10, 0.048, 0.018, 0.011, 0.939, 0.015],
    [12, 0.082, 0.017, 0.021, 0.935, 0.006],
    [7, 0.045, 0.015, 0.027, 0.954, 0.009],
    [12, 0.060, 0.014, 0.017, 0.921, 0.011];
  • и получает в observe результаты
    [-0.740, -0.757, -0.614, -0.476, -0.738, -0.747, -0.750, -0.766];
  • в итоге проверяющий код выставляет алгоритму оценку 109.78492, которая получается из минимума полученной метрики и границам, установленными авторами этого теста.

Заметим, что результаты, которые получает алгоритм, это отрицание точности классификации, так как в любом тесте ставится задача минимизации. На первой итерации наши предложения получают точность ~10%, что приблизительно соответствует случайной классификации 10 цифр. Но на последней итерации точности гораздо выше и достигают 76%.


Вы как участник должны реализовать следующий интерфейс. Он состоит из описанных выше методов инициализации (__init__), предложения наборов параметров (suggest) и обработки результатов (observe).


Как решать BBO


Одно из самых базовых вариантов решения такой задачи — это использование случайного поиска. Это метод и являлся baseline-ом, с которым сравнивались все предложенные решения. Для задачи с двумя параметрами рассмотренные этим методом наборы могут выглядеть так:



Техника довольно простая: мы знаем, сколько каких параметров, и какие значения они принимают. В __init__ мы запоминаем параметры и их диапазоны. На каждой итерации suggest мы сэмплируем 8 наборов из диапазонов и предлагаем их. Обработка результатов нас не интересует, поэтому observe оставляем пустым. Реализация этого метода представлена здесь.


Понятно, что метод далеко не оптимален, т.к. мы не учитываем результаты. Более того, алгоритм может предложить все наши 128 наборов в неоптимальном регионе, и мы так и не попробуем наборы из других регионов. Тем не менее, это уже способ, которым можно подбирать гиперпараметры, а не обучать модель только на первых установленных значениях.


Все же у многих поиск гиперпараметров ассоциируется с grid search-ем. И он является валидным решением задачи BBO. Grid search реализован во многих библиотеках. И, наверное, каждый, кто задумывается об оптимизации гиперпараметров для своей модели, следует ему. Вы для себя выбираете параметры, значения которых, как вам кажется, больше всего влияют на вашу модель, предполагаете их разумный диапазон, и отмечаете в нем несколько значений. Взяв каждую возможную комбинацию значений этих параметров, вы получаете grid или сетку поиска. Например, если у вас есть два гиперпараметра, и вы определили три значения для параметра 1 и три значения для параметра 2, то получится следующая сетка:



Обучив модель на каждой такой комбинации, вы оставляете лучший результат. В случае нашего интерфейса соревнования, в __init__ нужно сгенерировать такую сетку по описанию параметров, и в suggest предлагать еще не исследованные комбинации. Метод observe опять остается пустым.


Как же использовать результаты, возвращаемые алгоритму? Ведь понятно, что если мы сами последовательно подбираем гиперпараметры, то мы опираемся на результаты. Пусть мы попробовали два набора $S_1$ и $S_2$, и на наборе $S_1$ наша точность классификации составляет $92\%$, а на наборе $S_2$ — $54\%$. Мы не равнодушны к таким результатам. Вероятно, мы не будем больше пробовать обучить нашу модель на параметрах близких к $S_2$, а будем пробовать что-то близкое к $S_1$.


Наиболее популярным способом учета результатов является байесовская оптимизация. Оптимизация происходит из предположения о начальном распределении значений (prior), и с получением дополнительных результатов оно перестраивается (posterior). При использовании байесовской оптимизации в BBO чаще всего прибегают к гауссовским процессам. О них мы и поговорим далее.


Гауссовские процессы


С работой гауссовских процессов разберемся на примере задачи максимизации функции одной переменной $f$. Для оптимизации этой функции мы построим суррогатную модель $s$, которая будет приближать истинную функцию $f$. Описываться наша суррогатная модель будет гауссовским процессом. Значения $s$ будут совпадать с значениями $f$ в тех точках $x_i$, результаты которых мы знаем. Значения в остальных точках $x$ наша модель будет представлять распределениями, ведь мы не знаем их наверняка. Используя гауссовский процесс, эти распределения будут нормальными $\mathcal{N}(\mu,\sigma^2)$. Оценки на среднее $\mu$ и дисперсию $\sigma^2$ получаются из определения гауссовского процесса, который задается значениями в определенных точках и матрицей ковариаций с выбранным ядром. Более подробно про технику гауссовского процесса и нахождения $\mu$ и $\sigma^2$ можно почитать, например, в Википедии. Нам же будет важно его применение для оптимизации.


Рассмотрим теперь его применение к задаче максимизации функции одной переменной. После получения начальных точек и построения первой суррогатной модели, мы будет иметь что-то похожее на:



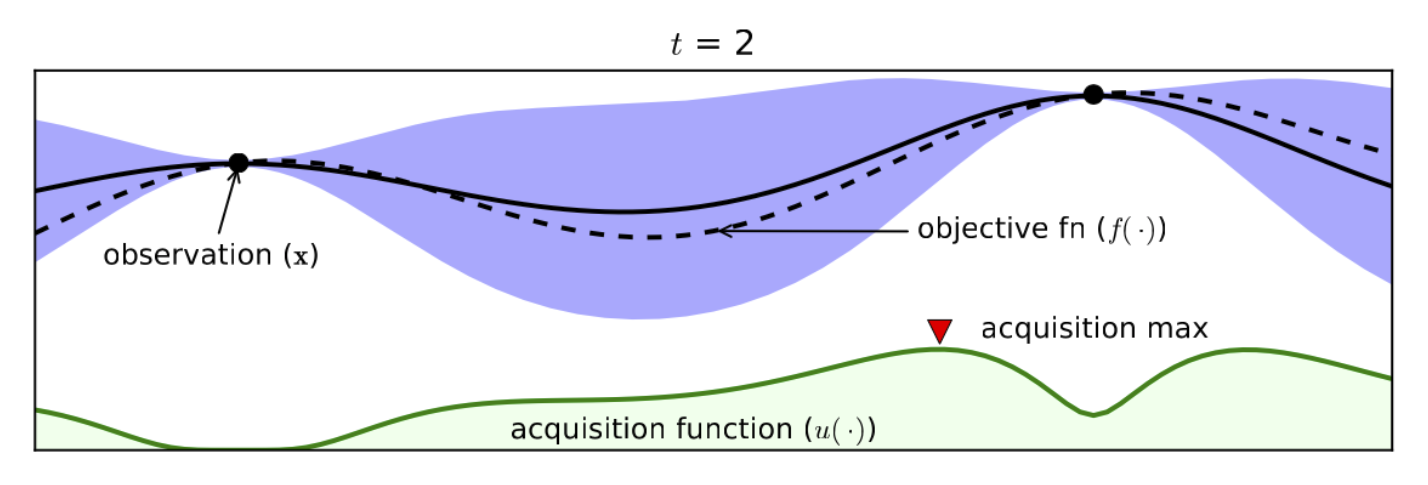
Здесь пунктирной линией показана истинная функция $f$, а сплошной — оценки на среднее значение суррогатной модели $s$. Синим фоном можно видеть оценку на отклонение значения от среднего. Для оптимизации функции нам нужно определиться, каким способом мы будем выбирать следующую точку. Эта стратегия обычно называется acquisition function или функцией приобретения. Существует множество способов выбора этой функцией. Наиболее популярными являются вероятность улучшения (Probability of Improvement, PI) и ожидаемое улучшение (Expected Improvement, EI). Они обе вычисляются по текущему оптимуму и оценке на среднее и дисперсию в точке. На рисунке в качестве следующей точки мы выбираем ту, у которой функция приобретения (на рисунке изображена зеленым цветом) максимальна, и предлагаем ее. Получив результат, мы видим следующее:



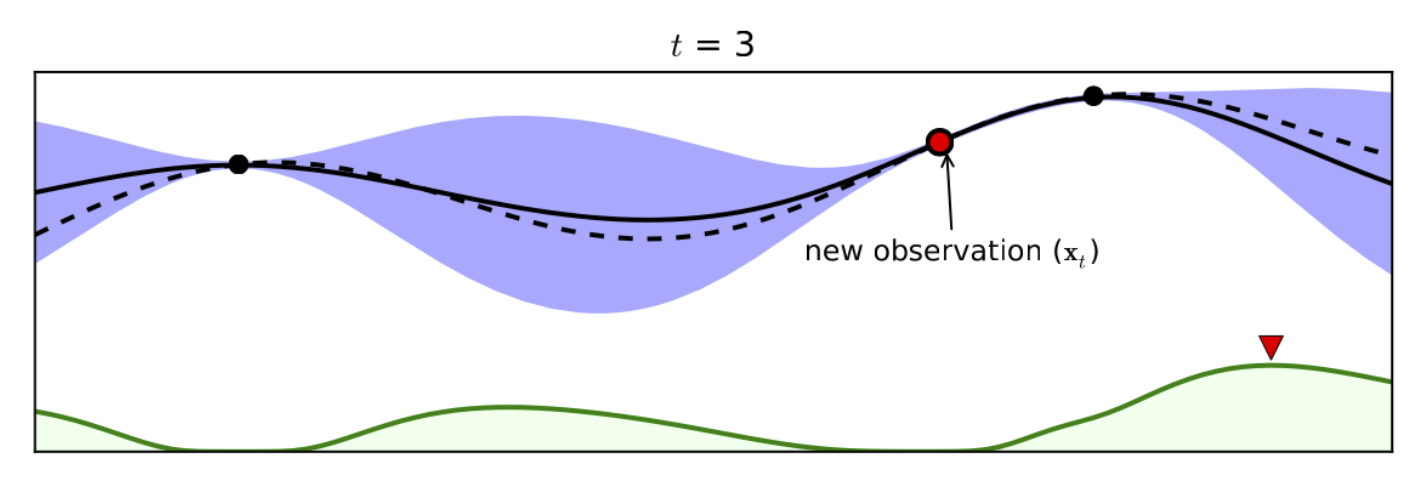
Добавляется новое наблюдение, и максимум функции приобретения переходит в другую точку, которую мы и запрашиваем далее:



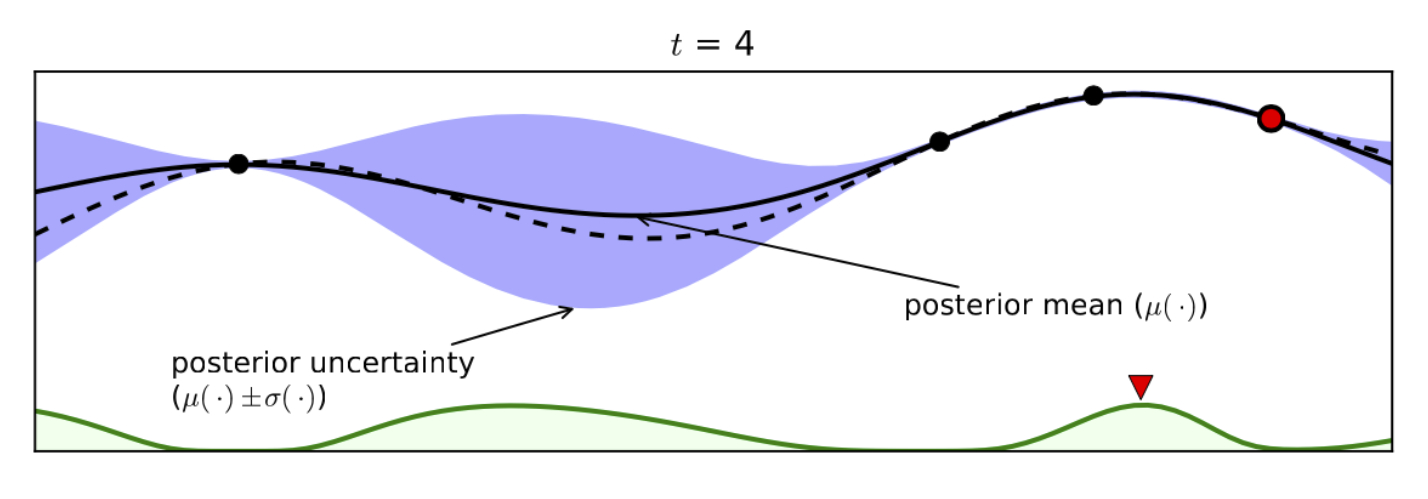
Таким образом происходит оптимизация, пока мы не достигнем предела итераций или наши улучшения станут незначительными. Гауссовский процесс также обобщается на несколько переменных.


В случае BBO нам нужно лишь проводить не максимизацию, а минимизацию, к которой легко перейти. В итоге имеем следующий алгоритм. В __init__ мы запоминаем наше пространство и преобразуем все переменные к вещественным значениям. Далее мы сэмплириуем (используя, например, Latin hypercube sampling) наборы для инициализации в течение нескольких первых итераций. В первых вызовах suggest мы предлагаем наши заготовленные наборы для инициализации. При вызове observe мы всегда лишь сохраняем пары $\{x_i, y_i\}$. А в дальнейших suggest мы поступаем следующим образом:


  1. Строим гауссовский процесс по уже имеющимся наблюдениям $\{x_i, y_i\}$.
  2. Сэмплируем какое-то количество кандидатов $n_{cand}$ (в нашем решении $n_{cand}=min(100*D, 5000)$, где $D$ — количество оптимизируемых параметров).
  3. Используя построенный гауссовский процесс, мы вычисляем оценки на средние и дисперсии значений в кандидатах.
  4. Вычисляем функцию приобретения в этих $n_{cand}$ кандидатах и выбираем 8 с наибольшими значениями.
  5. Возвращаем эти точки как наши предложения проверяющему коду.

Этот подход уже является сильным baseline-ом для задач, в которых нет явных ограничений на количество параметров и/или количество общих итераций.


Наш подход


Так как в соревновании все же было ограничение на количество итераций, и оно было равно 16, что довольно немного, мы решили упростить работу байесовской оптимизации.


В качестве подхода байесовской оптимизации мы использовали алгоритм TuRBO, которой является небольшим ответвлением от классических гауссовских процессов. Основное отличие состоит в том, что оптимизация проводится в доверительном регионе (откуда и название Trust Region Bayesian Optimization). Для интересующихся можно почитать оригинальную статью или код от организаторов соревнования.


Важной же частью нашего решения стало построение разбиения пространства гиперпараметров. Идея состоит в том, что если мы как-то ограничим все пространство допустимых значений, то байесовской модели будет проще получить хорошие результаты за столь малое количество итераций. В примере с методом k-ближайших соседей если мы каким-нибудь обучаемым методом поймем, что хорошее решение лежит в подпространстве, где $n_{neighbors}>50$ и $p\le2$, то имея меньшее пространство (а иногда и количество измерений), наша байесовская модель будет точнее.


Вот как этот обучаемый метод работает. Каждые 4 итерации (то есть не более 4 раз, т.к. всего имеем 16 итераций) мы перестраиваем разбиение всего пространства параметров. Пусть мы перестраиваем разбиение на итерации $t$ (от 1 to $16$), и у нас есть набор наблюдений $D_t$ который состоит из запрошенных нами точек и результатов $(x_1, y_1)$, ..., $(x_{n_t}, y_{n_t})$, где $n_t=8t$. Мы рекурсивно делим текущий набор наблюдений на левое и правое поддеревья. Деление выглядит следующим образом:


  1. Мы запускаем метод k-средних, чтобы разделить наши наблюдения на 2 кластера по значению метрики, которую мы пытается минимизировать. Под 1-ым кластером будем подразумевать точки с меньшим средним значением метрики, а под 2-ым — с большим.
  2. Использую эти метки кластеров, мы обучаем SVM модель, которая будет классифицировать точки в кластер 1 или 2. Мы знаем метки для текущих точек, и на них и обучаем модель.
  3. Так как у модели не всегда получается идеально приблизить метки, то наша SVM модель может классифицировать имеющиеся точки не так, как им были назначены кластера. Поэтому для каждой точки мы вычисляем ее кластер заново относительно SVM, и все точки с предсказаниями 1 отправляются в левое поддерево, а с 2 — в правое.

Мы продолжаем этот процесс рекурсивно пока не достигнем максимальной глубины $max_{depth}=5$, или количество точек в какой-то вершине станет недостаточным для инициализации байесовской модели в дальнейшем.


Исполнив этот метод, мы получаем дерево, в листьях которого расположены какие-то наборы точек, а в вершинах с детьми находятся SVM модели (критерии разбиения). Имея какую-то случайную точку, мы можем однозначно сопоставить ее с регионом нашего дерева, пройдя по этому дереву от корня до листа.


В этом разбиении более важно, что если мы хотим оптимизировать нашу функцию, то все листья в левом поддереве будут "перспективнее" в этом отношении, чем листья в правом поддереве (так как в левое мы направляли точки, которые соответствовали кластеру с меньшим средним значением метрики). Тогда после построения такого разбиения, мы выбираем регион, соответствующий самому левому листу, и проводим там байесовскую оптимизация до следующего перестроения.


К примеру, рассмотрим такое разбиение и работу TuRBO для модели SVM, у которой было выделено три параметра: коэффициент регуляризации $C$, параметр ядра $gamma$ и эпсилон для критерия остановки $tol$. Три параметра образуют трехмерное пространство. После разбиения пространства можно выделить два региона: точки, которые лежат в самом левом листе (зеленый цвет), и все остальные (красный цвет). Вот как это выглядит:



Темно-зеленым здесь отмечен доверительный регион TuRBO, и именно в нем и строится гауссовский процесс. Черным цветом обозначены 8 точек, которые будут возвращены нашим алгоритмом из suggest в рассматриваемой итерации.


Заключение


Все оставшиеся технические детали нашего решения можно найти в нашей статье. А код был опубликован на GitHub.


В этой статье мы поговорили о black box оптимизации, соревновании на эту тему, общие подходы к решениям и особенности нашего алгоритма, который занял третье место в этом соревновании.


Если вы хотите попробовать такие алгоритмы, то начальный код от авторов соревнования очень полезен. Запустить базовые решения можно, следуя инструкциям в этом репозитории.