22.03.2021 14:11
MarkWatney 2 1800 Источник


В настоящий момент появилось достаточно большое количество библиотек дополненной реальности с богатым функционалом (ARCore, ARKit, Vuforia). Тем не менее я решил начать свой открытый проект, попутно описывая как это работает изнутри. Если повезет, то позже получится добавить какой-то особый интересный функционал, которого нет в других библиотеках. В качестве целевых платформ пока возьмем Windows и Android. Библиотека пишется на C++, и сторонние библиотеки будут задействованы по минимуму, т.е. преимущественно не будет использовано ничего готового. Фокус в статьях будет направлен на алгоритмы и математику, которые постараюсь описать максимально доступно и подробно. В этой статье пойдет речь про основы векторной алгебры.


Дополненная реальность — это совмещение виртуального мира и реального. Для этого, нам нужно представить окружающее реальное пространство в виде математической модели, понимая закономерности которой, мы сможем получить данные для совмещения. Начнем с основ векторной алгебры.


Вектора — это частный случай матриц, состоящие либо из одного столбца, либо из одной строки. Когда мы говорим о векторе, обычно имеется вектор-столбец $\vec v = \begin{pmatrix}v_x \\ v_y \\ v_z \\v_w\end{pmatrix}$. Но записывать вектор как столбец неудобно, поэтому будем его транспонировать — $\vec v = \begin{pmatrix}v_x & v_y & v_z & v_w\end{pmatrix}^T$.


Длина вектора


Первое, что мы рассмотрим — получение длины вектора — $l = |\vec v|$, где $l$ — значение длины, $\vec v$ — наш вектор. Для примера возьмем двумерный вектор:

$\vec v = \begin{pmatrix}x & y\end{pmatrix}^T$, где $x$ и $y$ — компоненты вектора, значения проекций вектора на оси двумерных координат. И мы видим прямоугольный треугольник, где $x$ и $y$ — это длины катетов, а $l$ — длина его гипотенузы. По теореме Пифагора получается, что $l = \sqrt{x^2 + y^2}$. Значит $l = |\vec v| = \sqrt{x^2 + y^2}$. Вид формулы сохраняется и для векторов большей размерности, например — $l = |\vec v| = |\begin{pmatrix} x & y & z & w\end{pmatrix}^T| = \sqrt{x^2 + y^2 + z^2 + w^2}$.


Скалярное произведение


Скалярное произведение векторов — это сумма произведение их компонентов: $s = \vec a \cdot \vec b = a_x \cdot b_x + a_y \cdot b_y + a_z \cdot b_z$. Но так как мы знаем, что вектора — это матрицы, то тогда удобнее записать это в таком виде: $s = \vec{a}^T \vec{b}$. Это же произведение можно записать в другой форме: $s = {\vec a}^T \vec b = |\vec a| \cdot |\vec b| \cdot \cos{\delta}$, где $\delta$ — угол между векторами $\vec a$ и $\vec b$ (для двумерного случая эта формула доказывается через теорему косинусов). По этой формуле можно заключить, что скалярное произведение — это мера сонаправленности векторов. Ведь, если $\delta = 0^{\circ}$, то $\cos{\delta} = 1$, и $s$ — это просто произведение длин векторов. Так как $\cos{\delta}$ — не может быть больше 1, то это максимальное значение, которые мы можем получить, изменяя только угол $\delta$. Минимальное значение $\cos{\delta}$ будет равно -1, и получается при $\delta = 180^{\circ}$, т.е. когда вектора смотрят в противоположные направления. Также заметим, что при $\delta = 90^{\circ}$ $\cos{\delta}=0$, а значит какие бы длины не имели вектора $\vec a$ и $\vec b$, все равно $s = 0$. Можно в таком случае сказать, что вектора не имеют общего направления, и называются ортогональными.
Также при помощи скалярного произведения, мы можем записать формулу длины вектора красивее: $|\vec v| = \sqrt{\vec{v}^T \vec v}$, $|\vec v|^2 = \vec{v}^T \vec{v}$.


Проекция вектора на другой вектор


Возьмем два вектора: $\vec a$ и $\vec b$.
Проекцию вектора на другой вектор можно рассматривать в двух смыслах: геометрическом и алгебраическом. В геометрическом смысле проекция вектора на ось — это вектор, а в алгебраическом – число.



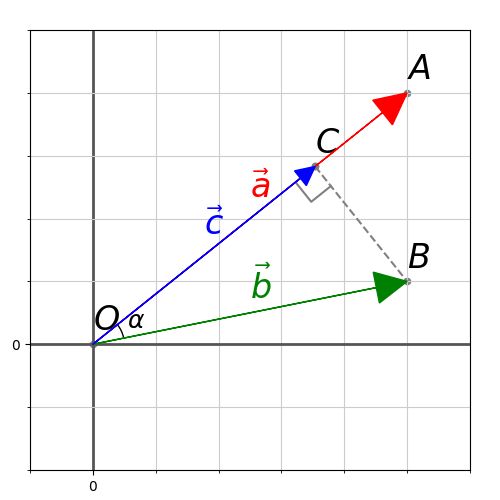
Вектора — это направления, поэтому их начало лежит в начале координат. Обозначим ключевые точки: $O$ — начало координат, $A$ — конечная точка вектора $\vec a$, $B$ — конечная точка вектора $\vec b$.


В геометрическом смысле мы ищем такой $\vec c$, чтобы конечная точка вектора (обозначим ее как — $C$) была ближайшей точкой к точке $B$, лежащей на прямой $OA$.


Иначе говоря, мы хотим найти составляющую $\vec b$ в $\vec a$, т.е. такое значение $t$, чтобы $\vec c = \vec a \cdot t$ и $|\vec c - \vec b| \rightarrow min$


Расстояние между точками $B$ и $C$ будет минимальным, если $\angle OCB = 90^\circ$. Получаем прямоугольный треугольник — $OCB$. Обозначим $\alpha = \angle COB$. Мы знаем, что $\cos{\alpha} = \frac{|OC|}{|OB|}$ по определению косинуса через соотношение сторон прямоугольного треугольника
($OB$ — гипотенуза, $OC$ — прилежащий катет).
Также возьмем скалярное произведение $s = \vec a \cdot \vec b = |\vec a| \cdot |\vec b| \cdot \cos{\alpha}$. Отсюда следует, что $\cos{\alpha} = \frac {\vec a \cdot \vec b } {|\vec a| \cdot |\vec b|}$. А значит $\frac{|OC|}{|OB|} = \frac {\vec a \cdot \vec b } {|\vec a| \cdot |\vec b|}$.


Тут вспоминаем, что $OC$ — это искомый вектор $\vec c$, а $OB$ — $\vec b$, и получаем $\frac{|\vec c|}{|\vec b|} = \frac {\vec a \cdot \vec b } {|\vec a| \cdot |\vec b|}$. Умножаем обе части на $|\vec b|$ и получаем — $|\vec c| = \frac {\vec a \cdot \vec b } {|\vec a|}$. Теперь мы знаем длину $\vec c$. Вектор $\vec c$ отличается от вектора $\vec a$ длинной, но не направлением, а значит через соотношение длин можно получить: $\vec c = \vec a \cdot \frac{|\vec c|}{|\vec a|}$. И мы можем вывести финальные формулы:
$t = \frac {\vec a \cdot \vec b } {|\vec a|^2} = \frac {{\vec a}^T \vec b}{{\vec a}^T \vec a}$ и
$\vec c = \vec a t = \vec a (\frac {{\vec a}^T \vec b}{{\vec a}^T \vec a})$


Нормализованный вектор


Хороший способ упростить работу над векторами — использовать вектора единичной длины. Возьмем вектор $\vec v$ и получим сонаправленный вектор $\vec{nv}$ единичной длины. Для этого вектор разделим на его длину: $\vec{nv} = \frac{\vec v}{|\vec v|}$. Эта операция называется нормализацией, а вектор — нормализованным.
Зная нормализованный вектор и длину исходного вектора, можно получить исходный вектор: $\vec v = \vec{nv} \cdot |\vec v|$.


Зная нормализованный вектор и исходный вектор, можно получить его длину: $|\vec v| = {\vec v}^T \vec{nv}$.


Хорошим преимуществом нормализованных векторов является то, что сильно упрощается формула проекции (т.к. длина равна 1, то она сокращается). Проекция вектора $\vec b$ на $\vec a$ единичной длины:
$t = \vec a \cdot \vec b = {\vec a}^T \vec b$
$\vec c = \vec a {(\vec a}^T \vec b)$


Матрица поворота двумерного пространства


Предположим у нас есть некая фигура:


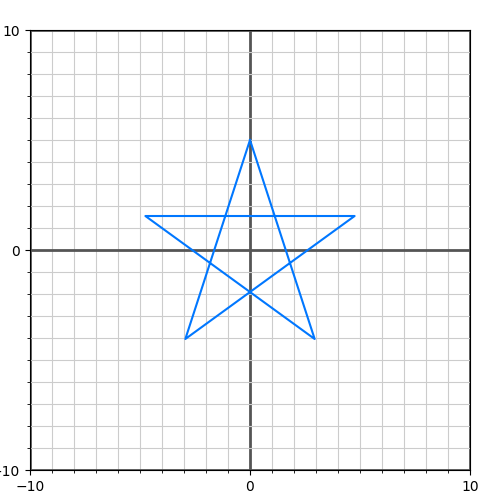
Figure


Чтобы ее нарисовать, заданы координаты ее вершин, от которых строятся линии. Координаты заданы в виде набора векторов следующим образом $\vec v_i = \begin{pmatrix}{v_i}_x & {v_i}_y \end{pmatrix}^T$. Наша координатная сетка задана двумя осями — единичными ортогональными (перпендикулярными) векторами. В двумерном пространстве можно получить два перпендикулярных вектора к другому вектору такой же длины следующим образом: $\perp \vec v = \begin{pmatrix}\mp v_y & \pm v_x \end{pmatrix}^T$ — левый и правый перпендикуляры. Берем вектор, задающим ось $X$ — $\vec{aX}=\begin{pmatrix} 1 & 0 \end{pmatrix}^T$ и ось $Y$ — левый к нему перпендикуляр — $\vec{aY}=\begin{pmatrix} 0 & 1 \end{pmatrix}^T$.
Выведем новый вектор, получаемый из наших базисный векторов:
$\vec{v'} = \vec{aX}^T \cdot v_x + \vec{aY}^T \cdot v_y = \begin{pmatrix} 1 & 0 \end{pmatrix}^T \cdot v_x + \begin{pmatrix} 0 & 1 \end{pmatrix}^T \cdot v_y = \begin{pmatrix} v_x & v_y \end{pmatrix}^T = \vec v$
Сюрприз — он совпадает с нашим исходным вектором.


Теперь попробуем как-то изменить нашу фигуру — повернем ее на угол $\alpha$. Для этого повернем векторы $\vec{aX}$ и $\vec{aY}$, задающих оси координат. Поворот вектора $\begin{pmatrix} 1 & 0 \end{pmatrix}^T$ задается косинусом и синусом угла — $\vec{aX}=rotate(\begin{pmatrix} 0 & 1 \end{pmatrix}^T, \alpha) = \begin{pmatrix} \cos{\alpha} & \sin{\alpha} \end{pmatrix}^T$. А чтобы получить вектор оси $Y$, возьмем перпендикуляр к $\vec{aX}$: $\vec{aY}=\perp \vec{aX}=\begin{pmatrix} -\sin{\alpha} & \cos{\alpha} \end{pmatrix}^T$. Выполнив эту трансформацию, получаем новую фигуру:
$\vec{v_i'} = \vec{aX} \cdot {v_i}_x + \vec{aY} \cdot {v_i}_y$


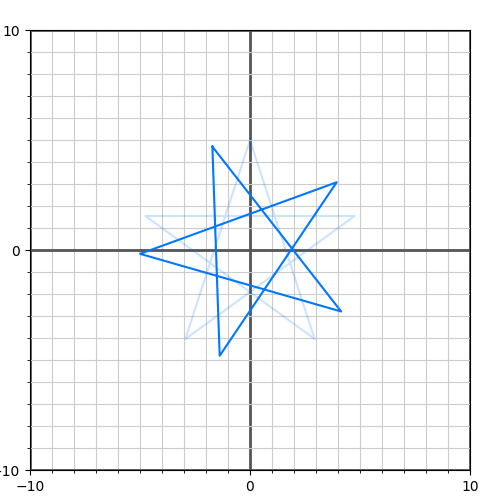
$<!-- math>$inline$\alpha=20^\circ$inline$</math -->$


Вектора $\vec{aX}$ и $\vec{aY}$ являются ортонормированным базисом, потому как вектора ортогональны между собой (а значит базис ортогонален), и вектора имеют единичную длину, т.е. нормированы.


Теперь мы говорим о нескольких системах координат — базовой системы координат (назовем ее мировой), и локальной для нашего объекта (которую мы поворачивали). Удобно объединить наш набор векторов в матрицу — $R = \begin{pmatrix} \vec{aX} & \vec{aY} \end{pmatrix} = \begin{pmatrix} \cos{\alpha} & -\sin{\alpha} \\ \sin{\alpha} & \cos{\alpha} \end{pmatrix}$
Тогда $\vec{v_i'} = \vec{aX} \cdot {v_i}_x + \vec{aY} \cdot {v_i}_y = \begin{pmatrix} \vec{aX} & \vec{aY} \end{pmatrix} \vec{v_i} = R \cdot \vec{v_i}$.


В итоге — $\vec{v_i'} = R \cdot \vec{v_i}$.


Матрица $R$, составляющая ортонормированный базис и описывающая поворот, называется матрицей поворота.


Также матрица поворота имеет ряд полезных свойств, которые следует иметь ввиду:


  • При $R = I$, где $I$ — единичная матрица, матрица соответствует нулевому повороту (угол $\alpha = 0$), и в таком случае локальные оси совпадают с мировыми. Как рассматривали выше, матрица никак не меняет исходный вектор.
  • $|R|=1$ — определитель матрицы равен 1, если у нас, как обычно бывает, правая тройка векторов. $|R| = -1$, если тройка векторов левая.
  • $R^T = R^{-1}$.
  • $R^T R = R^{-1} R = I$.
    $R^T R = \begin{pmatrix}\vec{aX} & \vec{aY}\end{pmatrix}^T \begin{pmatrix}\vec{aX} & \vec{aY}\end{pmatrix} = \begin{pmatrix}\vec{aX}^T\vec{aX} & \vec{aX}^T\vec{aY} \\ \vec{aY}^T\vec{aX} & \vec{aY}^T\vec{aY}\end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$.
  • $\vec{v'} = R \vec v \Rightarrow |\vec{v'}|=|\vec v|$, поворот не меняет длины вектора.
  • зная $\vec{v'}$ и $R$, можем получить исходный вектор $\vec v$ — $\vec v = R^{-1} \vec{v'} = R^T \vec{v'}$. Т.е. умножая вектор на матрицу поворота мы выполняем преобразование координат вектора из локальной системы координат объекта в мировую, но также мы можем поступать и наоборот — преобразовывать мировые координаты в локальную систему координат объекта, умножая на обратную матрицу поворота.

Теперь попробуем повернуть наш объект два раза, первый раз на угол $\alpha$, второй раз на угол $\beta$. Матрицу, полученную из угла $\alpha$, обозначим как $R_a$, из угла $\beta$ — $R_b$. Распишем наше итоговое преобразование:
$\vec{{v'}_i} = R_b R_a \vec{v_i}$.


$<!-- math>$inline$\alpha=20^\circ, \beta=10^\circ$inline$</math -->$


Обозначим $R_c = R_b R_a$, тогда $\vec{{v'}_i} = R_c \vec{v_i}$. И из двух операций мы получили одну. Так как поворот — это линейное преобразование (описали ее при помощи одной матрицы), множество преобразований можно описать одной матрицей, что сильно упрощает над ними работу.


Масштабирование в двумерном пространстве


Масштабировать объект достаточно просто, нужно только умножить координаты точек на коэффициент масштаба: $\vec{v_i'} = s \cdot \vec{v_i}$. Если мы хотим масштабировать объект на разную величину по разным осям, то формула принимает вид: $\vec{v_i'} = \begin{pmatrix} s_x \cdot {v_i}_x & s_y \cdot {v_i}_y \end{pmatrix}^T$. Для удобства переведем операцию в матричный вид: $S = \begin{pmatrix} s_x & 0 \\ 0 & s_y \end{pmatrix}, \vec{v_i'} = S \cdot \vec{v_i}$.


Теперь предположим, что нам нужно повернуть и масштабировать наш объект. Нужно отметить, что если сначала масштабировать, а затем повернуть, то результат будет отличаться, от того результата, где мы сначала повернули, а затем масштабировали:


Сначала поворот, а затем масштабирование по осям:


$<!-- math>$inline$\alpha=20^\circ, s_x=1.5, s_y=0.5$inline$</math -->$


Сначала масштабирование по осям, а затем поворот:


$<!-- math>$inline$\alpha=20^\circ, s_x=1.5, s_y=0.5$inline$</math -->$


Как мы видим порядок операций играет большое значение, и его нужно обязательно учитывать.
Также здесь мы также можем объединять матрицы преобразования в одну:
$\vec{{v'}_i} = S R \vec{v_i}, \space T_a = S R \space \Rightarrow \space \vec{{v'}_i} = T_a \vec{v_i}$
$\vec{{v'}_i} = R S \vec{v_i}, \space T_b = R S \space \Rightarrow \space \vec{{v'}_i} = T_b \vec{v_i}$
$T_a \neq T_b!$


Хотя в данном случае, если $s_x = s_y$, то $T_a = T_b$. Тем не менее, с порядком преобразований нужно быть очень аккуратным. Их нельзя просто так менять местами.


Векторное произведение векторов


Перейдем в трехмерное пространство и рассмотрим определенное на нем векторное произведение.
Векторное произведение двух векторов в трёхмерном пространстве — вектор, ортогональный к обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.


Для примера возьмем два трехмерных вектора — $\vec a$, $\vec b$. И в результате векторного произведения получим $\vec c = \vec a \times \vec b = \begin{pmatrix}a_y \cdot b_z - a_z \cdot b_y & a_z \cdot b_x - a_x \cdot b_z & a_x \cdot b_y - a_y \cdot b_x \end{pmatrix}^T$


Визуализируем данную операцию:



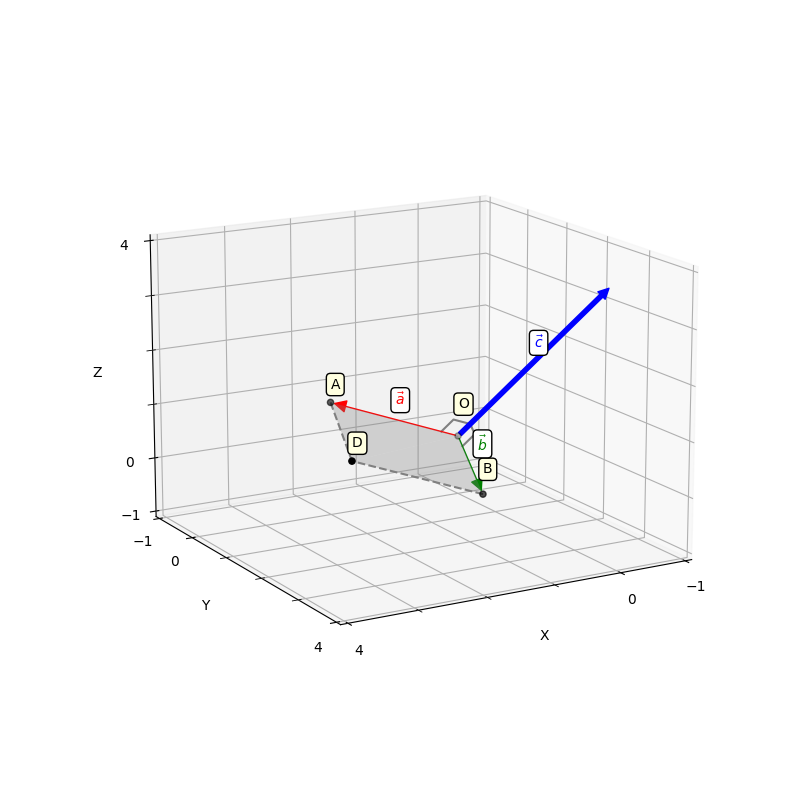
Здесь наши вектора $\vec a$, $\vec b$ и $\vec c$. Вектора начинаются с начала координат, обозначенной точкой $O$. Конечная точка вектора $\vec a$ — точка $A$. Конечная точка $\vec b$ — точка $B$. Параллелограмм из определения формируются точками $O$, $A$, $B$, $D$. Координаты точки $D$ находим как — $D = \vec a + \vec b$. В итоге имеем следующие соотношения:


  • $|\vec c| = S(OABD)$, где $S$ — площадь,
  • $\vec{a}^T \vec c = 0$,
  • $\vec{b}^T \vec c = 0$.

Два вектора образуют плоскость, а векторное произведение позволяет получить перпендикуляр к этой плоскости. Получившиеся вектора образуют образуют правую тройку векторов. Если берем обратный вектор, то получаем второй перпендикуляр к плоскости, и тройка векторов будет уже левой.


Для запоминания этой формулы удобно использовать мнемонический определитель. Пусть $i = \begin{pmatrix} 1 & 0 & 0 \end{pmatrix}^T, \space j = \begin{pmatrix} 0 & 1 & 0 \end{pmatrix}^T, \space k = \begin{pmatrix} 0 & 0 & 1 \end{pmatrix}^T$, и мы раскладываем определить по строке как сумму определителей миноров исходной матрицы $i, j, k$:
$\vec c = \vec a \times \vec b = \begin{vmatrix} (i, j, k)^T & \vec a & \vec b \end{vmatrix} = \begin{vmatrix} i & a_x & b_x \\ j & a_y & b_y \\ k & a_z & b_z \end{vmatrix} = i \cdot \begin{vmatrix} a_y & b_y \\ a_z & b_z \end{vmatrix} - j \cdot \begin{vmatrix} a_x & b_x \\ a_z & b_z \end{vmatrix} + k \cdot \begin{vmatrix} a_x & b_x \\ a_y & b_y \end{vmatrix} \space \Rightarrow$
$\vec c = \begin{pmatrix}a_y \cdot b_z - a_z \cdot b_y & a_z \cdot b_x - a_x \cdot b_z & a_x \cdot b_y - a_y \cdot b_x \end{pmatrix}^T$


Некоторые удобные свойства данного произведения:


  • Если два вектора ортогональны и нормализованы, то вектор также будет иметь единичную длину. Параллелограмм, который образуется двумя исходными векторами, станет квадратом с длинной сторон равной единице. Т.е. площадь равна единице, отсюда длина выходного вектора — единица.
  • $\vec a \times \vec b = - \vec b \times \vec a$

Матрица поворота трехмерного пространства.


С тем, как формировать матрицу в двумерном пространстве мы разобрались. В трехмерном она формируется уже не двумя, а тремя ортогональными векторами — $R = \begin{pmatrix} \vec{aX} & \vec{aY} & \vec{aZ} \end{pmatrix}$. По свойствам, описанным выше, можно вывести следующие отношения между этими векторам:


  • $\vec{aZ} = \vec{aX} \times \vec{aY}$
  • $\vec{aX} = \vec{aY} \times \vec{aZ}$
  • $\vec{aY} = \vec{aZ} \times \vec{aX}$

Вычислить вектора этих осей сложнее, чем в матрице поворота двумерного пространства. Для примера получения этих векторов рассмотрим алгоритм, который в трехмерных движках называется lookAt. Для этого нам понадобятся вектор направления взгляда — $\vec z$ и опорный вектор для оси $Y$ — $\vec y$. Сам алгоритм:


  1. Обычно направление камеры совпадает с осью $Z$. Поэтому нормализуем $\vec z$ и получаем ось $Z$ — $\vec aZ = \frac{\vec z}{|\vec z|}$.
  2. Получаем вектор оси $X$ — $\vec{aX} = \frac{\vec{y} \times \vec{aZ}}{|\vec{y} \times \vec{aZ}|}$. В итоге у нас есть два нормализованных ортогональных вектора $\vec{aX}$ и $\vec{aZ}$, описывающих оси $X$ и $Z$, при этом ось $Z$ сонаправлена с входным вектором $\vec z$, а ось $X$ перпендикулярна к входному опорному вектору $\vec y$.
  3. Получаем вектор оси $Y$ из полученных $\vec{aX}$ и $\vec{aZ}$ — $\vec{aY} = \vec{aZ} \times \vec{aX}$.
  4. В итоге $R = \begin{pmatrix} \vec{aX} & \vec{aY} & \vec{aZ} \end{pmatrix}$

В трехмерных редакторах и движках в интерфейсах часто используются углы Эйлера для задания поворота. Углы Эйлера более интуитивно понятны — это три числа, обозначающие три последовательных поворота вокруг трех основных осей $X, Y, Z$. Однако, работать с ними не очень то просто. Если попробовать выразить итоговый вектор напрямую через эти повороты, то получим довольно объемную формулу, состоящую из синусов и косинусов наших углов. Есть еще пара проблем с этими углами. Первая проблема — это то, что сами по себе углы не задают однозначного поворота, так как результат зависит от того, в какой последовательности происходили повороты — $X \rightarrow Y \rightarrow Z$ или $Z \rightarrow X \rightarrow Y$ или как-то еще. Углы Эйлера — это последовательность поворотов, а как мы помним, смена порядка трансформаций меняет итоговый результат. Вторая проблема — это gimbal lock.


Внутри же трехмерные движки чаще всего используют кватернионы, которых мы касаться не будем.


Существуют разные способы задания поворота в трехмерном пространстве, и каждый имеет свои плюсы и минусы:


  • Матрица поворота. С ней просто работать (т.к. это просто матрицы). Но есть логическая избыточность данных — все элементы матрицы связаны определенными условиями, так как количество элементов больше степеней свободы (12 элементов против трех степеней). Т.е. мы не можем взять матрицу и наполнить ее случайными числами, так при несоблюдении условий матрица просто не будет являться матрицей поворота.
  • Углы Эйлера. Они интуитивно понятны, но работать с ними сложно.
  • Вектор оси вращения и угол порота вокруг нее. Любой возможный поворот можно описать таким образом. Поворота вектора вокруг заданной оси рассмотрим ниже.
  • Вектор поворота Родрига. Это трехмерный вектор, где нормализованный вектор представляет собой ось вращения, а длина вектора угол поворота. Этот способ задания поворота похож на предыдущий способ, но количество элементов здесь равно числу степеней свободы, и элементы не связаны между собой жесткими ограничениями. И мы можем взять трехмерный вектор с абсолютно случайными числами, и любой полученный вектор будет задавать какое-то возможное вращение.

Поворот вектора вокруг заданной оси


Теперь рассмотрим операцию, позволяющую реализовать поворот вектора вокруг оси.


Возьмем вектор $\vec n$ — описывающий ось, вокруг которой нужно повернуть вектор $\vec v$ на угол $\alpha$. Результирующий вектор обозначим как $\vec{v'} = rotate(\vec n, \alpha, \vec v)$. Иллюстрируем процесс:



Вектор $\vec n$ мы можем разложить сумму векторов: вектора, параллельный к вектору $\vec n$ — $\vec{v_\parallel}$, и вектора, перпендикулярному к вектору к вектору $\vec n$ — $\vec{v_{\perp}}$.
$\vec v = \vec{v_{\parallel}} + \vec{v_{\perp}}$.
Вектор $\vec{v_\parallel}$ — это проекция вектора $\vec v$ на вектор $\vec n$. Т.к. $\vec n$ — нормализованный вектор, то:
$\vec{v_\parallel} = \vec{n} (\vec{n}^T \vec{v})$
Та часть $\vec v$, которая принадлежит оси вращения ($\vec{v_{\parallel}}$) не измениться во время вращения. Повернуть нам нужно только $\vec{v_{\perp}}$ в плоскости перпендикулярной к $\vec n$ на угол $\alpha$, Обозначим этот вектор как $\vec{v_{\perp rot}}$. Тогда наш искомый вектор — $\vec{v'} = \vec{v_\parallel} + \vec{v_{\perp rot}}$.
Вектор $\vec{v_{\perp}}$ можем найти следующим образом:
$\vec{v_{\perp}} = \vec v - \vec{v_\parallel}$
Для того, чтобы повернуть $\vec{v_{\perp}}$, выведем оси $X$ и $Y$ в плоскости, в которой будем выполнять поворот. Это должны быть два ортогональных нормализованных вектора, ортогональных к $\vec n$. Один ортогональный вектор у нас уже есть — $\vec{v_{\perp}}$, нормализуем его и обозначим как ось $X$ — $\vec{aX} = \frac{\vec{v_{\perp}}}{|\vec{v_{\perp}}|}$.


Теперь получим вектор оси $Y$. Это должен быть вектор, ортогональный к $\vec n$ и $\vec{aX}$ (т.е. и к $\vec{v_{\perp}}$). Получить его можно через векторное произведение: $\vec{d_y} = \vec n \times \vec{v_{\perp}}$. Значит $\vec{aY} = \frac{\vec{d_y}}{|\vec{d_y}|}$. По свойству векторного произведения $|\vec{d_y}|$ будет равно площади параллелограмма, образуемого двумя исходными векторами ($\vec n$ и $\vec{aX}$). Так как вектора ортогональны, то у нас будет не параллелограмм, а прямоугольник, а значит $|\vec{d_y}| = |\vec{n}| \cdot |\vec{v_{\perp}}|$. $|\vec{n}| = 1 \space \Rightarrow \space |\vec{d_y}| = |\vec{v_{\perp}}|$. Значит $\vec{aY} = \frac{\vec n \times \vec{v_{\perp}}}{|\vec{v_{\perp}}|}$.
Поворот двумерного вектора $\vec v = \begin{pmatrix} 1 & 0 \end{pmatrix}^T$ на угол $\alpha$ можно получить через синус и косинус — $rotate2D(\vec v, \alpha) = \begin{pmatrix} \cos{\alpha} & \sin{\alpha} \end{pmatrix}^T$. Т.к. $\vec{v_{\perp}}$ в координатах полученной плоскости сонаправлен с осью $X$, то он будет равен $\begin{pmatrix} |\vec{v_{\perp}}| & 0 \end{pmatrix}^T = \begin{pmatrix} 1 & 0 \end{pmatrix}^T \cdot |\vec{v_{\perp}}|$. Этот вектор после поворота — $rotate2D(\begin{pmatrix} 0 & 1 \end{pmatrix}^T, \alpha) \cdot |\vec{v_{\perp}}| = \begin{pmatrix} \cos{\alpha} & \sin{\alpha} \end{pmatrix}^T \cdot |\vec{v_{\perp}}|$. Отсюда можем вывести: $\vec{v_{\perp rot}} = (\vec{aX} \cdot \cos{\alpha} + \vec{aY} \cdot \sin{\alpha}) \cdot |\vec{v_{\perp}}|$ $\space \Rightarrow \space$
$\vec{v_{\perp rot}} = (\frac{\vec{v_{\perp}}}{|\vec{v_{\perp}}|} \cdot \cos{\alpha} + \frac{\vec n \times \vec{v_{\perp}}}{|\vec{v_{\perp}}|} \cdot \sin{\alpha}) \cdot |\vec{v_{\perp}}|$ $\space \Rightarrow \space$
$\vec{v_{\perp rot}} = \vec{v_{\perp}} \cdot \cos{\alpha} + (\vec n \times \vec{v_{\perp}}) \cdot \sin{\alpha}$
Теперь мы можем получить наш искомый вектор:
$\vec{v'} = \vec{v_{\parallel}} + \vec{v_{\perp rot}} = \vec{v_{\parallel}} + \vec{v_{\perp}} \cdot \cos{\alpha} + (\vec n \times \vec{v_{\perp}}) \cdot \sin{\alpha}$


Мы разобрались с тем, как поворачивать вектор вокруг заданной оси на заданный угол, значит теперь мы умеем использовать поворот, заданный таким образом.


Получить вектор оси вращения и угол из вектора Родрига не составляет большого труда, а значит мы теперь умеем работать и с ним тоже.


Напоминаю, что матрица поворота представляет собой три базисных вектора $R = \begin{pmatrix} \vec{aX} & \vec{aY} & \vec{aZ} \end{pmatrix}$, а углы Эйлера — три последовательных поворота вокруг осей $X$, $Y$, $Z$. Значит мы можем взять единичную матрицу, как нулевой поворот $R_0 = I$, а затем последовательно поворачивать базисные вектора вокруг нужных нам осей. В результате получим матрицу поворота соответствующую углам Эйлера. Например:
$\vec{aX'} = rotate((0, 0, 1)^T, angle_z, rotate((0, 1, 0)^T, angle_y, rotate((1, 0, 0)^T, angle_x, \vec{aX})))$
$\vec{aY'} = rotate((0, 0, 1)^T, angle_z, rotate((0, 1, 0)^T, angle_y, rotate((1, 0, 0)^T, angle_x, \vec{aY})))$
$\vec{aZ'} = rotate((0, 0, 1)^T, angle_z, rotate((0, 1, 0)^T, angle_y, rotate((1, 0, 0)^T, angle_x, \vec{aZ})))$
$R = \begin{pmatrix} \vec{aX'} & \vec{aY'} & \vec{aZ'} \end{pmatrix}$
$rotateEuler(angle_x, angle_y, angle_z, v) = R \cdot \vec v$
Также можно отдельно вывести матрицы вращения по каждой из осей $X$, $Y$, $Z$ ($R_x$, $R_Y$, $R_z$ соответственно) и получить итоговую матрицу последовательным их умножением:
$R = R_x \cdot R_y \cdot R_z$


Таким же образом можно перевести вектор поворота Родрига в матрицу поворота: также поворачиваем оси матрицы поворота, полученные от единичной матрицы.


Итак, с вращением объекта разобрались. Переходим к остальным трансформациям.


Масштабирование в трехмерном пространстве


Все тоже самое что и двумерном пространстве, только матрица масштабирования принимает вид: $S = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{pmatrix}$


Перемещение объекта


До этого момента точка начала локальных координат не смещалась в мировом пространстве. Так как точка начала координат нашего объекта — это его центр, то центр объект никуда не смещался. Реализовать это смещение просто: $\vec{v'_i} = \vec{v_i} + \vec t$, где $\vec t$ — вектор, задающий смещение.


Теперь мы умеем масштабировать объект по осям, поворачивать его и перемещать.
Объединим все одной формулой: $\vec{v'_i} = R \cdot S \cdot \vec{v_i} + \vec t$:


s_x = 0.5, \space s_y = 0.5, \space $<!-- math>$inline$\alpha={30^{\circ}}, \space \vec t = \begin{pmatrix} 6 & 4 \end{pmatrix}^T$inline$</math -->$


Чтобы упростить формулу, мы можем, как уже делали ранее, объединить матрицы $T = R \cdot S \space \Rightarrow \space \vec{v'_i} = T \cdot \vec{v_i} + \vec t$. В итоге наше преобразование описывает матрица $T$ и вектор $\vec t$. Объединение вектора $\vec t$ с матрицей $T$ еще более бы упростило формулу, однако сделать в данном случае не получится, потому как сложение здесь — это не линейная операция. Тем не менее сделать это возможно, и рассмотрим этот момент уже в следующей статье.


Заключение


Для какого-то покажется, что статья описывает очевидные вещи, кому-то может показаться наоборот немного запутанной. Тем не менее это базовый фундамент, на котором будет строиться все остальное. Векторная алгебра — является фундаментом для многих областей, так что статья может вам оказаться полезной не только в дополненной реальности. Следующая статья будет уже более узконаправленной.