У науки есть огромное, бесконечное число достоинств, и одно из них состоит в том, что именно она способна кратко, точно и ёмко ответить на самые неожиданные в своей простоте, детские вопросы. Например: «Почему барабан круглый?» Если у вас есть дети или вы сами в детстве задавались этим вопросом, то в этом переводе, которым мы решили поделиться к старту флагманского курса о Data Science, вы найдёте два ответа: первый — подробный, в формулах, второй — краткий, понятный ребёнку ответ.

Я всегда был очарован тем, как свойства любой формы волны связаны с тем, как мы их воспринимаем. Особенно форма волн и формы, от которых волны исходят. Мы знаем, что звук — это механическая волна и для её распространения нужна среда. Источник вибрации перемещает молекулы воздуха колебаниями, вызывающими сжатие и разрежение (области высокого и низкого давления). Эти изменения давления взаимодействуют с нашей барабанной перепонкой, и мы воспринимаем звук. Итак, если все виды вибраций вызывают вибрацию только молекул воздуха, то в свойствах формы волны должно быть что-то особенное, что помогает нам различать два звука. Что заставляет гитару звучать иначе, чем пианино, или почему мой голос отличается от вашего.

Я рассмотрю эту проблему с двух точек зрения. В первом подходе я сравниваю два реальных образца из разных инструментов и анализирую их свойства. Во втором — я работаю с нуля и показываю, как решения волновых уравнений в различных сценариях проявляются в этих свойствах, которые мы воспринимаем.

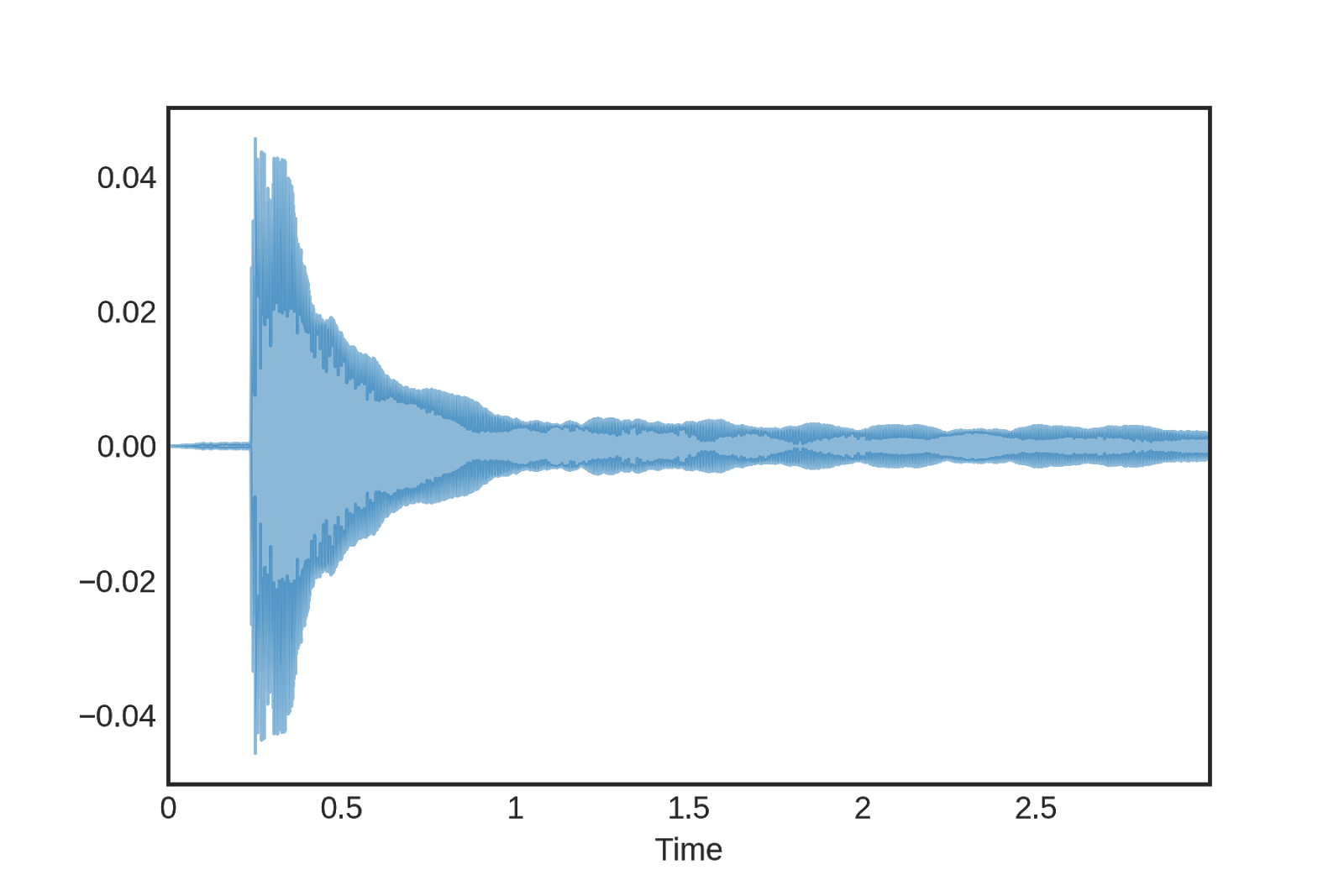
Пианино — это струнный инструмент. Вибрации начинаются с удара молотка по его струнам. Такое же поведение наблюдается и на графике формы волны. Молоток создаёт высокую импульсную силу на струнах, и в результате происходит внезапное увеличение амплитуды. Со временем амплитуда и, следовательно, громкость сигнала затухают.

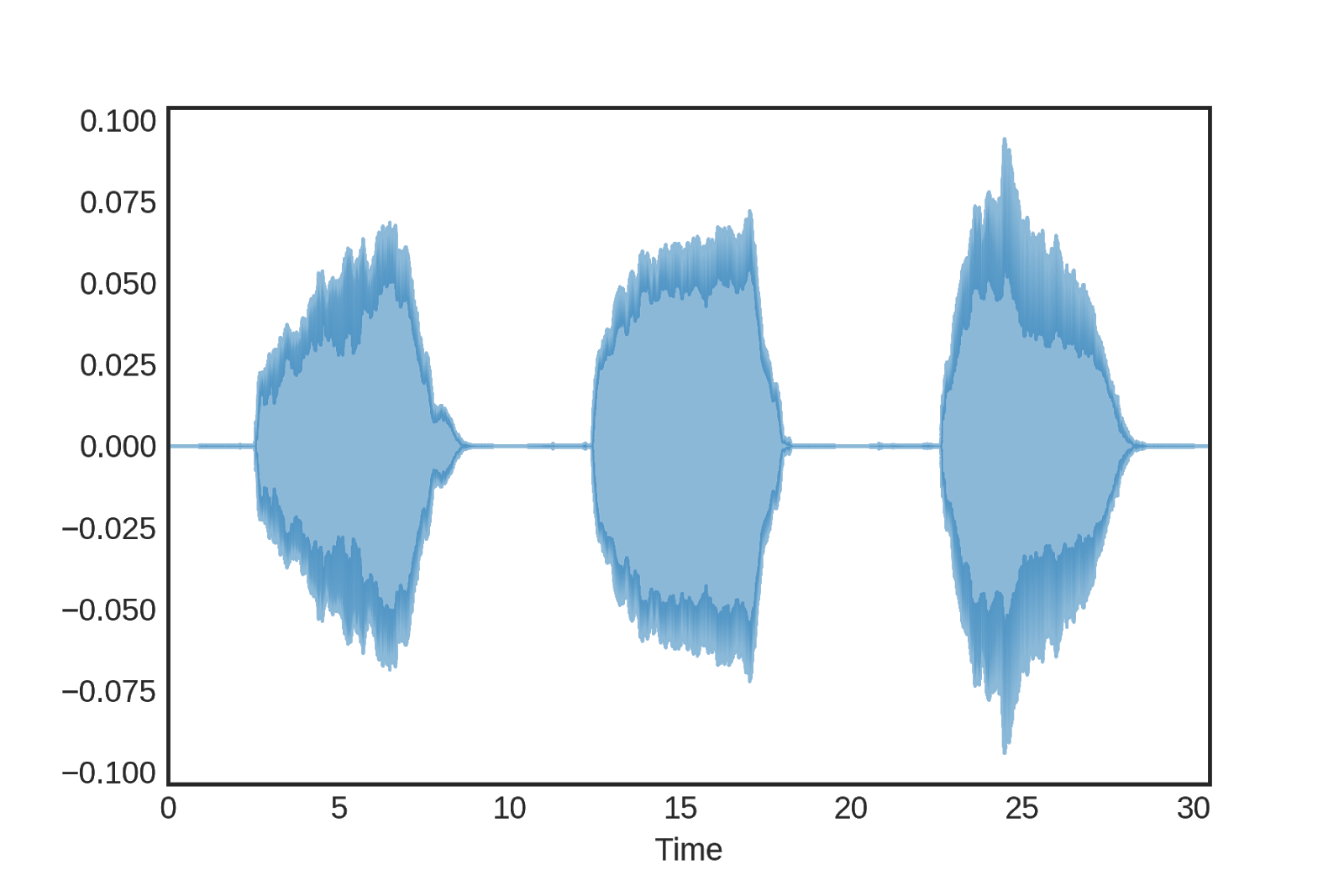
На рисунке визуализированы звуки скрипичных нот [включая полутон в середине, который по историческим причинам не считается нотой с формальной точки зрения, поэтому в названии вы видите диапазон A4-B4, все звуки в нём не обозначены] с возрастающей частотой. Частотные характеристики не фиксируются на графике формы волны, но формы отличаются от пианино. В отличие от пианино амплитуда всех нот постепенно увеличивается, так как звук издаётся смычком, который мягко трётся о струну. И уменьшение амплитуды происходит тоже резко, поскольку скрипач приглушает одну струну, играя на другой. И поэтому мы не слышим никакого протяжного звука или какой-то филировки, как мы называем это в музыке.

Чтобы найти больше различий в звуке, мы должны перейти в область частот. Лучший способ увидеть такие различия — спектрограмма, т. е. визуальное представление спектра частот по мере изменения сигнала во времени. Для создания спектрограммы аудиосигнал разбивается на более мелкие сегменты, и к каждому из этих сегментов может применяться быстрое преобразование Фурье. Давайте вначале рассмотрим простую синусоидальную волну с частотой 440 Гц.

Синусоидальная волна с частотой 440 Гц

Тон синусоидальной волны и тон пианино находятся точно в одной и той же высоте, на частоте 440 Гц. Однако синусоидальную волну слушать не так интересно. Звучит как просто непрерывный тон звука без какой-либо динамики или насыщенности. Хотя многие интересные звуки возможно получить путём интерференции и применения преобразований на синусоидах. Синтезатор — это устройство, позволяющее вам сделать это.

import numpy as np 
import matplotlib.pyplot as plt
import librosa, librosa.display
sr = 22050 # sample rate
T = 2.0    # seconds
t = np.linspace(0, T, int(T*sr)) # time variable
x = 0.5*np.sin(2*np.pi*440*t)
def plot_spectrogram(signal, name):

    spectrogram =     librosa.amplitude_to_db(np.abs(librosa.stft(signal)))
    plt.figure(figsize=(10, 5))
    librosa.display.specshow(spectrogram, y_axis="log")
    plt.colorbar(format="%+2.0f dB")
    plt.title(f"Log-frequency power spectrogram for {name}")
    plt.xlabel("Time")
    plt.show()
plot_spectrogram(x, 'sine wave')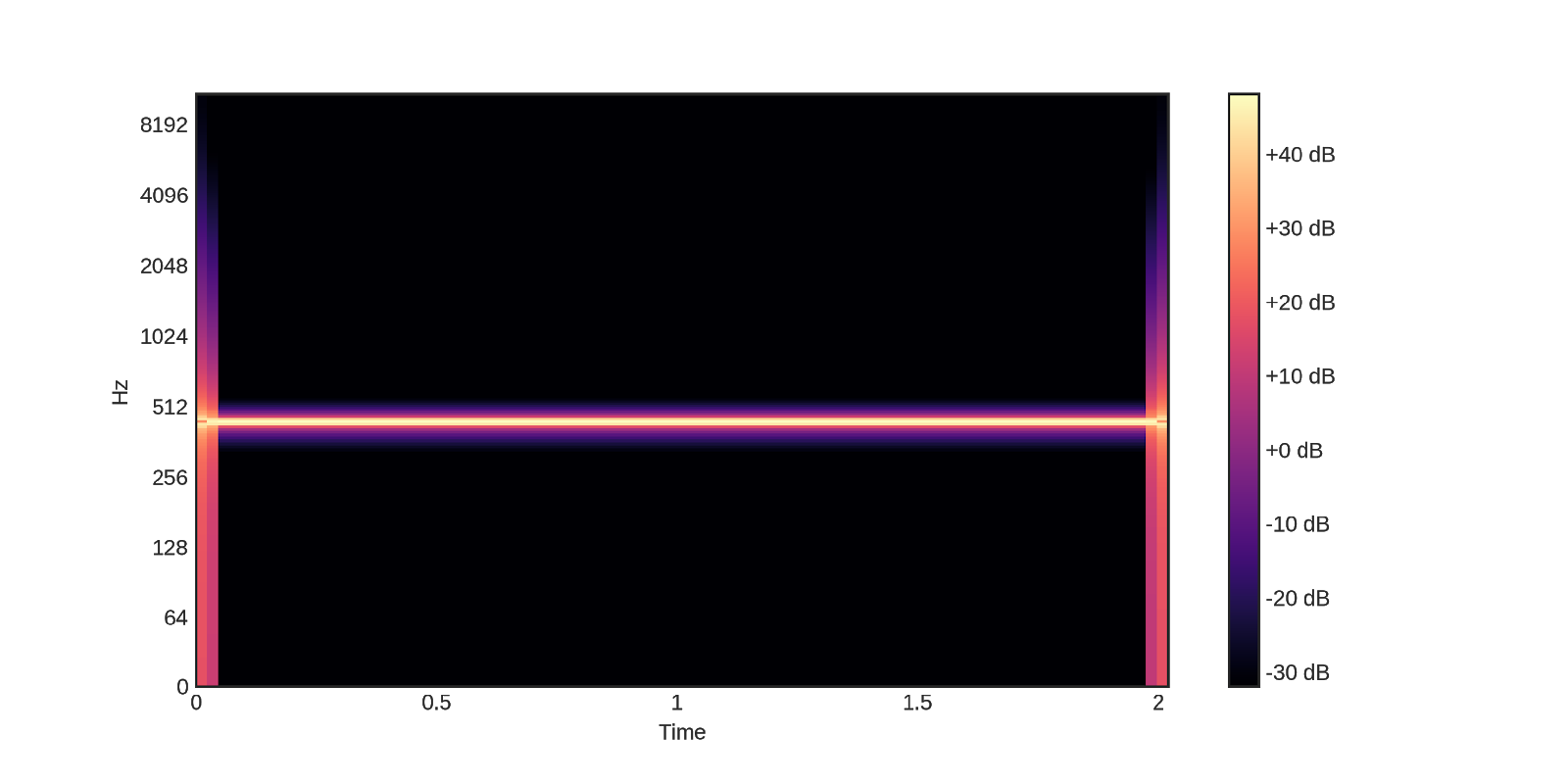

Наблюдая спектрограмму синусоидальной волны, можно обнаружить, что единственная присутствующая частота составляет 440 Гц.

piano, srp = librosa.load('Piano.mf.A4_trimmed.wav')
violin, srv = librosa.load('Violin.arco.mf.sulA.A4B4.wav')
plot_spectrogram(piano, 'piano')
plot_spectrogram(violin, 'violin')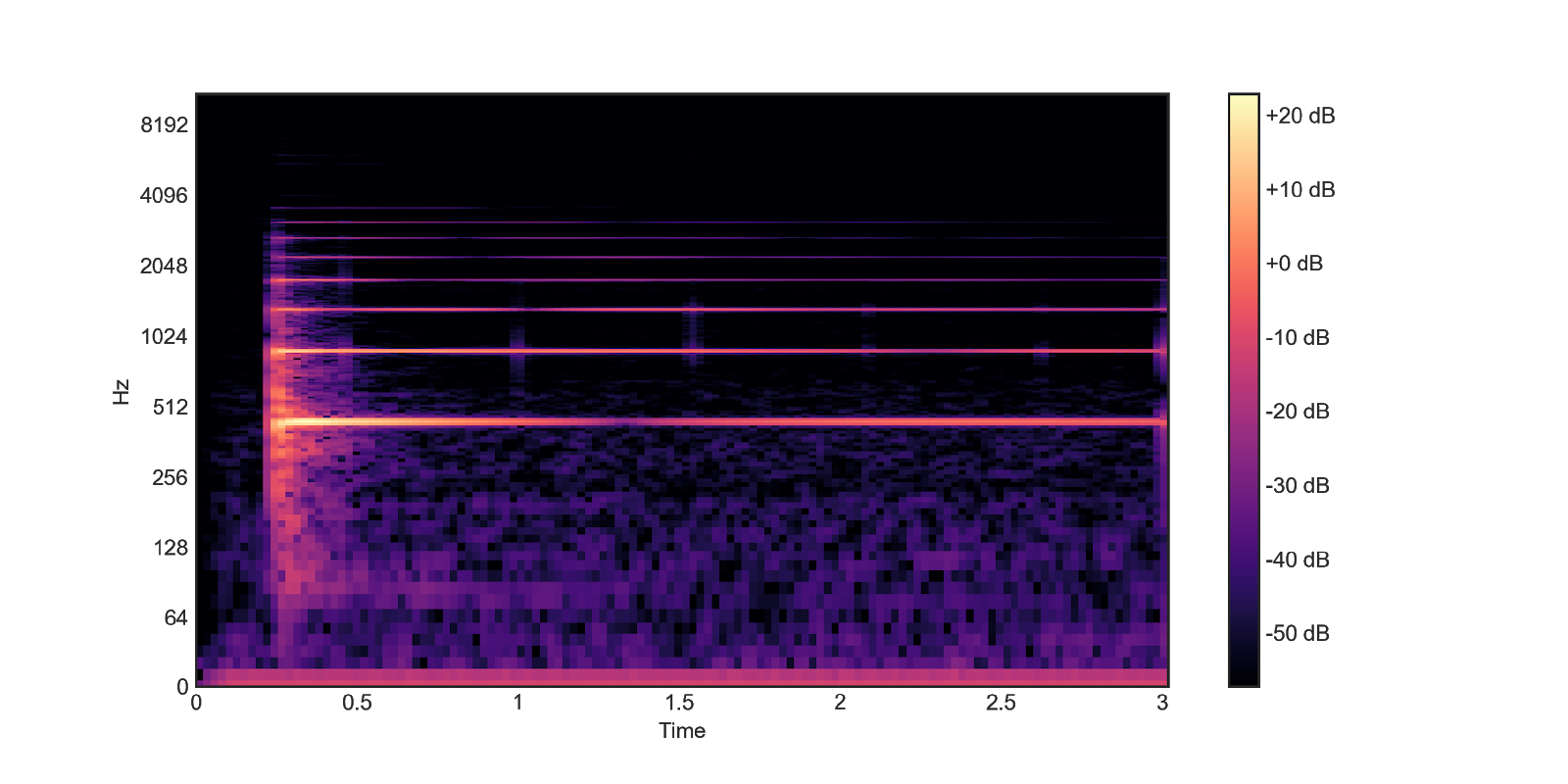

Построив спектрограмму пианино, мы увидим, что наиболее доминирующая частота составляет 440 Гц, но в то же время присутствует множество других частот. Они известны как обертоны, и для одной вибрирующей струны можно показать, что эти обертоны на самом деле являются целыми кратными основной частоте, в данном случае 440 Гц.

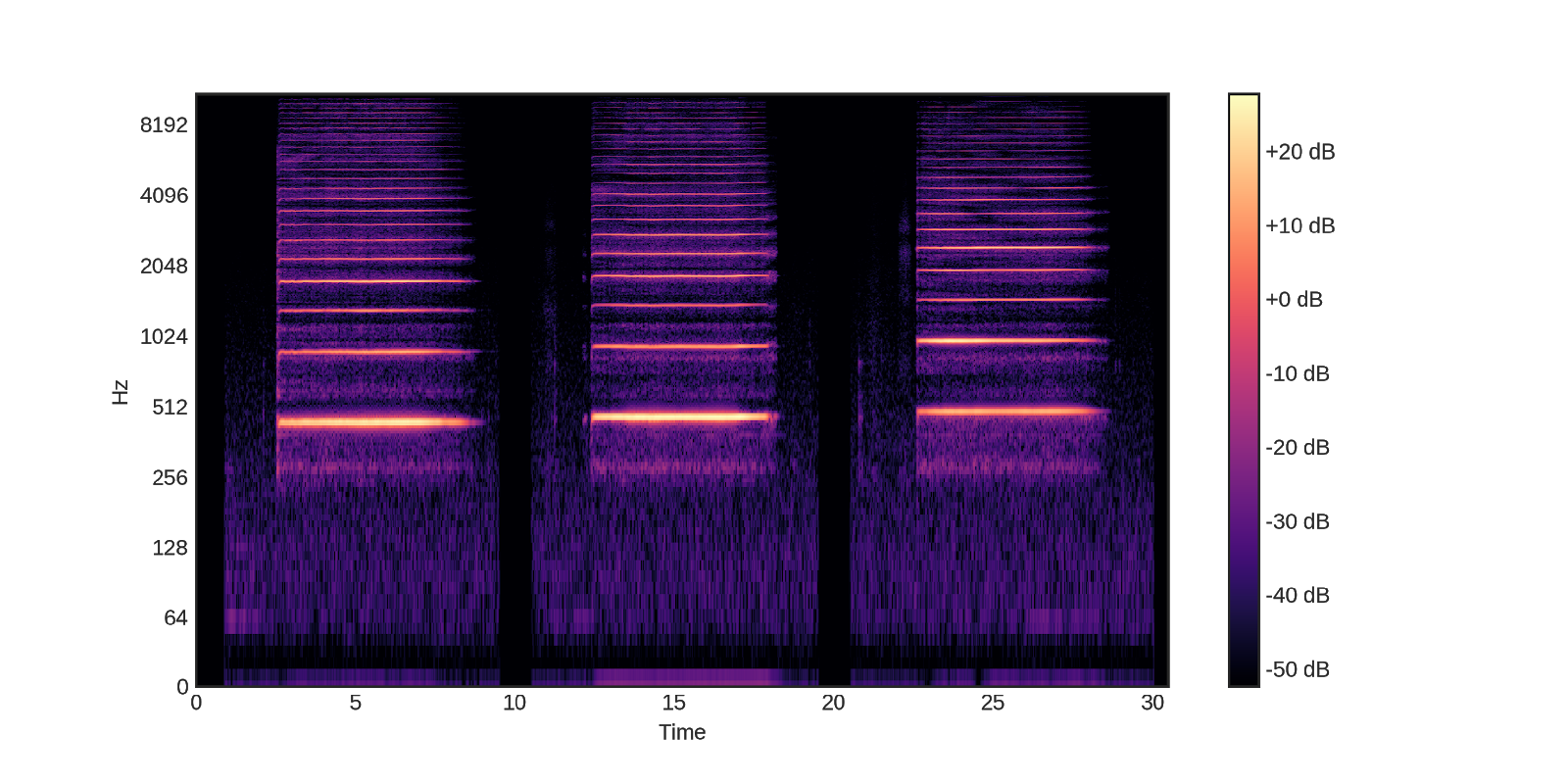
В случае скрипки на спектрограмме та же история. Есть основная частота, а затем — обертоны во всех трёх сыгранных нотах. Количество обертонов намного выше, чем на спектрограмме пианино. И это одна из причин того, почему пианино звучит иначе, чем скрипка, хотя оба они являются струнными инструментами. Основная частота увеличивается по мере перехода от первой ноты к третьей сыгранной ноте. Также здесь обертоны — целые числа, кратные основной частоте.

Таким образом, можно сказать, что частота обертонов имеет какое-то отношение к тональному качеству звука. Играя одну ноту на струнном инструменте, мы видим, что в звуке присутствуют кратные основной частоте целые числа. Если эти обертоны не находятся в целых кратных числах или в определённых соотношениях частот (как, например, когда на множестве клавиш исполняются аккорды), человеческому уху трудно различить, имеет ли звук какое-либо тональное качество или нет.

Вернёмся к первоначальному вопросу. Почему большинство барабанов круглой формы? От табла, конго, бонго до обычной ударной установки — всё круглое. Что такого особенного в круглой или прямоугольной форме? Чтобы разобраться в этом, нам придётся взглянуть на вибрации, исходящие от прямоугольной мембраны, и посмотреть, сможем ли мы что-то обобщить.

Предположим, что мембрана установлена в плоскости xy, а u(x, y, t) — вертикальный прогиб мембраны относительно положения равновесия (x, y) во времени t. При постоянном t поверхность z = u(x, y, t) задаёт форму мембраны в момент t.

Рассмотрим натянутую мембрану, закреплённую на прямоугольной раме длиной a и шириной b. Чтобы изучить её колебания, нужно решить задачу о начальном значении.

Здесь уравнения (2) и (3) — граничные значения, а уравнения (4) и (5) — начальные значения. Чтобы найти простые решения, мы можем воспользоваться разделением переменных, удовлетворяющих гомогенным граничным условиям, а затем применить принцип суперпозиции для построения серии решений, удовлетворяющих также и начальным условиям. Мы можем искать решения вида u (x, y, t) = X (x)Y (y)T (t). Подставив формулу в уравнение (1), получаем:

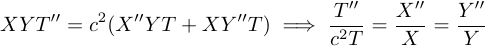
Поскольку обе стороны уравнения — функции независимых переменных, они должны быть равны константе.

Компонент времени упорядочен, но компоненты пространства снова содержат функции несвязанных переменных с обеих сторон уравнения. Можно приравнять их к константе, вот так:

Имея ввиду C = A-B,  эти уравнения можно переписать так:

Теперь решения этих двух однородных дифференциалов могут быть либо суммой экспоненциальных функций, либо суммой синусоид, в зависимости от знака B и C. Поскольку волны периодичны по своей природе, а мембрана в определённом месте не может просто продолжать увеличиваться, чтобы решение было периодическим по своей природе, B и C должны быть положительными константами.

??? в формуле известны как характерные частоты мембраны. Теперь точное решение волнового уравнения можно записать в виде произведения X (x), Y (y) и T (t), а коэффициенты возможно оценить при помощи свойств ряда Фурье. Нас больше интересует не поиск точного решения волнового уравнения, а выяснение звучания обертонов таких частотных характеристик. Если ради простоты предположить, что мембрана квадратная, то a = b, следовательно:

Здесь мы ясно видим, что в отличие от вибрирующей струны высшие обертоны не являются целыми кратными основной частоты. Вот почему вибрирующая струна обладает тональным качеством, а исходящий от прямоугольной мембраны звук не является тональным. Когда происходит произвольный удар в прямоугольный барабан, в процессе одновременно представлено множество мод колебаний, но различные слышимые частоты не являются целыми кратными одной и той же частоты.

Круглая мембрана — это немного другая история. При помощи аналогичных вычислений можно показать, что на самом деле обертоны — это целые кратные основной частоты. Более подробную информацию можно найти в этой замечательной книге по дифференциальным уравнениям.

Перед тем как играть на индийских классических ударных инструментах, таких как табла, пахавадж и т. д., музыкант настраивает эти инструменты на мажорную гамму, в которой будет исполняться вокальное или инструментальное произведение. Он натягивает или ослабляет круглую мембрану, на которой будет играть. Всё это возможно ещё и потому, что конструкция мембраны позволяет ей обладать тональным качеством — а значит, её можно настраивать. Если бы мембрана имела прямоугольную форму, настроить её было бы невозможно. Такие инструменты имеют многовековую историю, их круглая форма — не случайность!

Эта статья напоминает, что с помощью анализа данных, а также зная математические формулировки тех или иных процессов, можно смотреть на эти процессы с различных точек зрения и отвечать на неожиданные в своей простоте вопросы. Если вам интересно работать с данными, выявлять неочевидное, то вы можете обратить внимание на наш флагманский курс Data Science, где можно не только освоить профессию дата-сайентиста с нуля, но и прокачать ваши навыки в ней.

Узнайте, как прокачаться и в других специальностях или освоить их с нуля:

• Профессия Data Scientist

• Профессия Data Analyst

• Курс по Data Engineering