Timsort: Очень быстрый, O(n log n), стабильный алгоритм сортировки, созданный для реального мира, а не для академических целей.

Timsort — это алгоритм сортировки, который эффективен для реальных данных, а не создан в академической лаборатории. Tim Peters создал Timsort для Python в 2001 году. 

Timsort сначала анализирует список, который он пытается отсортировать, и на его основе выбирает наилучший подход. С момента его появления он используется в качестве алгоритма сортировки по умолчанию в Python, Java, платформе Android и GNU Octave.

Нотация Big O для Timsort — это O(n log n). Чтобы узнать о нотации Big O, прочтите это.

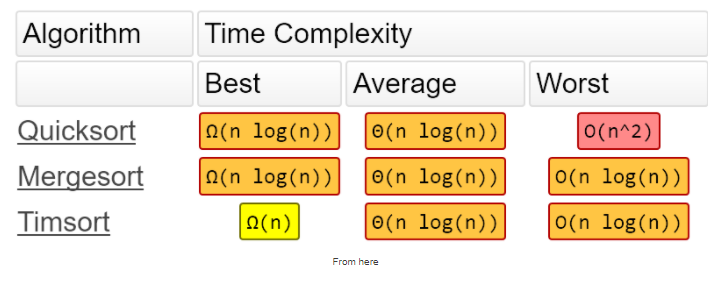
Время сортировки Timsort такое же, как и у Mergesort, что быстрее, чем у большинства других известных сортировок. Timsort фактически использует сортировку вставкой как и Mergesort. Вы это скоро увидите.

Peters разработал Timsort для использования уже упорядоченных элементов, которые существуют в большинстве реальных наборов данных. Он называет эти упорядоченные элементы "natural runs" (естественные пробеги). Они итеративно перебирают данные, собирая элементы в пробеги и одновременно объединяя несколько этих пробегов в один.

Если массив (array), который мы пытаемся отсортировать, содержит менее 64 элементов, Timsort выполняет сортировку вставкой.

Сортировка вставкой — это простая сортировка, которая наиболее эффективна для небольших списков. Она функционирует довольно медленно при работе с большими списками, но при этом быстро работает с маленькими списками. Идея сортировки вставкой заключается в следующем:

• Просматривать элементы по одному

• Построить отсортированный список, вставляя элемент в нужное место

Вот таблица, показывающая, как сортировка вставкой сортирует список [34, 10, 64, 51, 32, 21].

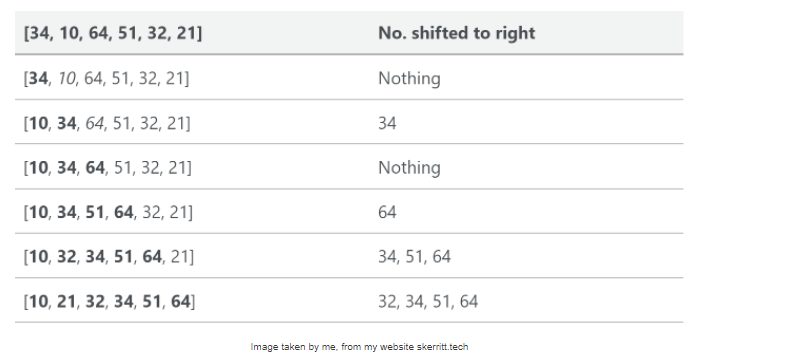
В данном случае мы вставляем только что отсортированные элементы в новый подмассив (sub-array), который начинается от начала массива.

Вот gif, показывающий сортировку вставкой:

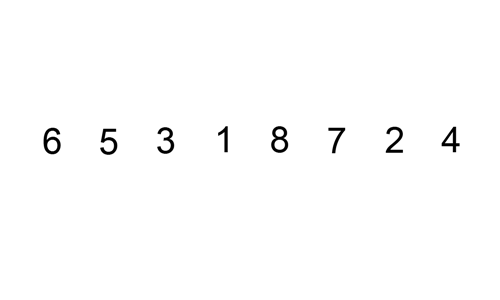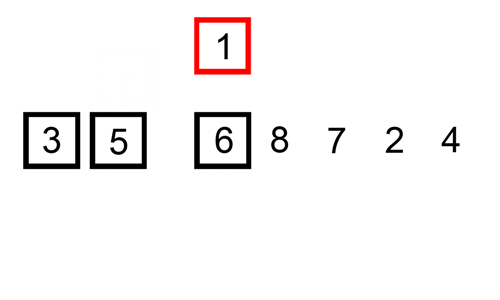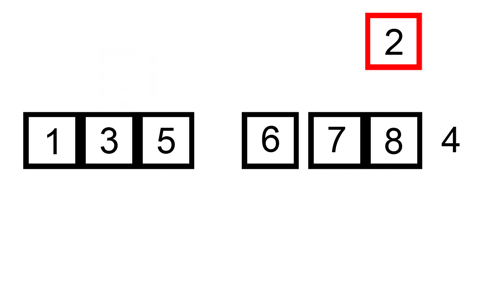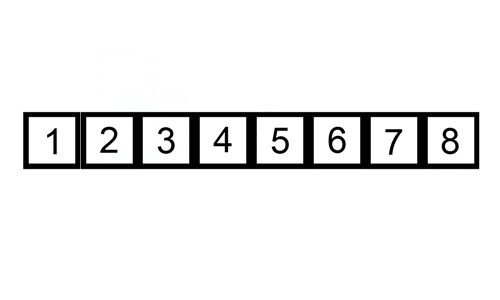
Больше о пробегах

Если список больше 64 элементов, то алгоритм сделает первый проход (pass) по списку в поисках частей, которые строго возрастают или убывают. Если какая-либо часть является убывающей, то она будет изменена.

Таким образом, если пробег уменьшается, он будет выглядеть следующим образом (пробег выделен жирным шрифтом):

Если не происходит уменьшение, то это будет выглядеть следующим образом:

Minrun - это размер, который определяется на основе размера массива. Алгоритм выбирает его таким образом, чтобы большинство пробегов в произвольном массиве были или становились длиной minrun. Слияние двух массивов более эффективно, когда число пробегов равно или чуть меньше степени числа 2. Timsort выбирает minrun, чтобы попытаться обеспечить эту эффективность, убедившись, что minrun равен или меньше степени числа 2.

Алгоритм выбирает minrun из диапазона от 32 до 64 включительно, таким образом, чтобы длина исходного массива при расчете была меньше или равна степени числа 2.

Если длина пробега меньше minrun, необходимо рассчитать длину этого пробега относительно minrun. Используя это новое число выполняется сортировка вставкой для создания нового пробега.

Итак, если minrun равен 63, а длина пробега равна 33, вы выполняете вычитание: 63-33 = 30. Затем вы берете 30 элементов из run[33], и делаете сортировку вставкой для создания нового пробега.

После завершения этой части должно появиться множество отсортированных пробегов в списке.

Слияние

Теперь Timsort использует сортировку слиянием, чтобы объединить пробеги. Однако Timsort следит за тем, чтобы сохранить стабильность и баланс слияния во время сортировки.

Для поддержания стабильности мы не должны менять местами два одинаковых числа. Это не только сохраняет их исходные позиции в списке, но и позволяет алгоритму работать быстрее. В ближайшее время мы обсудим баланс слияния.

Когда Timsort находит пробеги, он добавляет их в стек. Простой стек выглядит следующим образом:

Представьте себе стопку тарелок. Вы не можете взять тарелки снизу, поэтому вам приходится брать их сверху. То же самое можно сказать и о стеке.

Timsort пытается сбалансировать две конкурирующие задачи при сортировке слиянием. С одной стороны, мы хотели бы отложить слияние на как можно дольше, чтобы использовать паттерны, которые могут появиться позже, но еще больше нам хотелось бы произвести слияние как можно быстрее, чтобы воспользоваться тем, что только что найденный пробег все еще находится наверху в иерархии памяти. Мы также не можем откладывать слияние "слишком надолго", потому что на запоминание еще не объединенных пробегов расходуется память, а стек имеет фиксированный размер.

Чтобы добиться компромисса, Timsort отслеживает три последних элемента в стеке и создает два правила, которые должны выполняться для этих элементов:

1. A > B + C

2. B > C

Где A, B и C - три самых последних элемента в стеке.

По словам Tim Peters:

Хорошим компромиссом оказалось то, что сохраняет два варианта для записей в стеке, где A, B и C - длины трех самых правых еще не объединенных частей.

Обычно объединить соседние пробеги разной длины очень сложно. Еще сложнее то, что мы должны поддерживать стабильность. Чтобы обойти эту проблему, Timsort выделяет временную память. Он помещает меньший (называя оба пробега A и B) из двух побегов в эту временную память.

Galloping*

*Модификация процедуры слияния подмассивов

Пока Timsort объединяет A и B, обнаруживается, что один пробег "выигрывает" много раз подряд. Если бы оказалось, что A состоял из гораздо меньших чисел, чем B, то A оказался бы на прежнем месте. Слияние этих двух пробегов потребовало бы много работы c нулевым результатом.

Чаще всего данные имеют некоторую уже существующую внутреннюю структуру. Timsort предполагает, что если многие значения пробега A меньше, чем значения пробега B, то, скорее всего, A будет и дальше содержать меньшие значения, чем B.

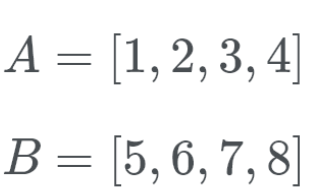
Затем Timsort переходит в режим galloping. Вместо того чтобы сверять A[0] и B[0] друг с другом, Timsort выполняет бинарный поиск соответствующей позиции b[0] в a[0]. Таким образом, Timsort может полностью переместить A. Затем Timsort ищет соответствующее местоположение A[0] в B. После этого Timsort также может полностью перемещает B.

Давайте посмотрим на это в действии. Timsort проверяет B[0] (который равен 5) и, используя бинарный поиск, ищет соответствующее место в A.

Итак, B[0] находится в конце списка A. Теперь Timsort проверяет A[0] (который равен 1) в правильном месте B. Итак, мы ищем, где находится число 1. Это число находится в начале B. Теперь мы знаем, что B находится в конце A, а A - в начале B.

Оказывается, что действие не имеет смысла, если подходящее место для B[0] находится очень близко к началу A (или наоборот), поэтому режим gallop быстро завершается, если он не приносит результатов. Кроме того, Timsort принимает это к сведению и усложняет вход в режим gallop, увеличивая количество последовательных "побед" только в A или только в B. Если режим gallop приносит результаты, Timsort облегчает его повторный запуск.

Если говорить коротко, Timsort делает две вещи невероятно хорошо:

• Обеспечивает высокую производительность при работе с массивами с уже существующей внутренней структурой

• Создает возможность поддерживать стабильную сортировку

А раньше, чтобы добиться стабильной сортировки, вам нужно было сжать элементы списка в целые числа и отсортировать его как массив кортежей.

Код

Если вас не интересует код, смело пропускайте эту часть. Под этим разделом есть дополнительная информация.

Если вы хотите увидеть оригинальный исходный код Timsort во всей его красе, посмотрите его здесь. Timsort официально реализован на C, а не на Python.

Timsort фактически встроен прямо в Python, поэтому этот код служит только в качестве пояснения. Чтобы использовать Timsort, просто напишите следующее:

list.sort()

Или

sorted(list)

Если вы хотите узнать, как работает Timsort, и понять его суть, я настоятельно рекомендую вам попробовать применить его самостоятельно!

Эта статья основана на оригинальном вступлении Tim Peters к Timsort, которое можно найти здесь.

Перевод статьи подготовлен в рамках курса «Алгоритмы и структуры данных».

Если вам интересно узнать о курсе больше, приглашаем на день открытых дверей онлайн.