05.07.2021 21:46
janatem 2 733 Источник
stream rate art
Measuring of stream rate in an artist's impression.

In one of our previous publications, we talked about a way to measure event stream rate using a counter based on exponential decay. It turns out that the idea of such a counter has an interesting generalization. This paper by Artem Shvorin and Dmitry Kamaldinov, Qrator Labs, reveals it.

Our immersion plan is as follows. First, let us look at and analyze a few examples of how events are counted and the rate of the stream is estimated in general. The next step is to see a generalization, namely some class of counters, which we call the u-model. Next, we explore what useful properties u-models have and propose a technique for constructing an adequate rate estimate.

1   Examples of Counters


Without limiting the generality, we may assume that an event counter is described by its state $s$, which, upon the arrival of an event at time $t$, is updated according to some rule:

$ s\mathop{\mapsto}^t s'. $


The state is not necessarily expressed by a number, but for feasibility reasons we may assume that it is representable by a finite set of bits.

In some cases, events are weighted, and the weight of the event $w$ must be taken into account when updating the state:

$ s\mathop{\mapsto}^{t,w} s'. $


But at first, we will consider simple unweighted events, and we will add weight later when we need it. That will not be difficult at all.

In this article, we will limit ourselves to considering only deterministic counters, that is, those for which the update rule is given by a function $s'=update(s,t)$. But in general, it may be useful to add some randomness to this mechanism; we recently talked about it [7] and will probably continue to do so.

It should also be possible, knowing the state of the counter, to estimate the rate of the stream. Generally speaking, the notion of stream rate is non-trivial, and we will discuss it in more detail later. For now, we will just assume that the counter model has some nominal estimate as a function $r(s,t)$, written out of some design considerations.

1.1   Linear Counters: Counting All Events


The simplest thing one may think of is to just count the number of events that have occurred since we started. That is, when an event arrives, we do this:

$ s \mapsto s + 1. $


We will call such counters linear.

The estimate is the average rate over the entire history:

$ r(s,t) = s/t. $



Some problem may occur due to counter overflow. There are also questions about defining the estimate: here, very old events have the same effect on the rate estimate as recent ones.

1.1.1   Sliding Window Event Counting


To eliminate the above drawbacks of linear counters, one may count the number of events not since the creation of the world but only those that occurred no more than $T$ cycles ago. This time interval of length $T$ is usually called a window, and it is sliding because it shifts a step forward with each cycle.

A naive implementation assumes to remember all events in the window, thus requiring $O(T)$ of memory. However, there are ways to save resources in trade-off for reduced precision, such as described in [6]. The update rule is expressed in a rather complicated way, while the average rate over time $T$ serves as the estimate:

$ r(s,t) = s/T. $



Unfortunately, such linear counters are unsuitable for our purposes: we can still tolerate a decrease in accuracy, but $O(\log T)$ in memory and complexity is too costly, even for small $T$.

1.2   EDecay: the Exponential Decay


The idea of the decay counter is inspired by the well-known concept of radioactive decay [4]. Its essence is that the amount of undecayed matter decreases over time according to an exponential law:

$v(t) = v_0 e^{-\lambda t},$


where $v_0$ is the amount of matter at the initial (zero) moment of time, $\lambda$ is some parameter, the so-called decay constant.

It is more convenient to rewrite this expression in the following form:

$v(t) = v_0 \alpha^{-t},$


replacing the parameter. For more details on parameterization of counter models, see Section A of the Appendix.

Relying on this mechanism, we can build an event counter as described in our article [1].
By definition, we will assume that each type of event corresponds to the value of $v$, which has a physical meaning of “quantity of matter” and depends on time in such a way that it sharply increases by one at the occurrence of the event and decreases in the remaining time in accordance with the exponential law shown above.

That is, to account for a new event arriving at time $t$, one must first apply the decay and then increase the counter by one:

$ \begin{equation*} v_{new}(t) = v(t) + 1 \equiv v(t_0)\alpha^{-(t - t_0)} + 1, \end{equation*} $


where $t_0$ is the arrival time of the previous event.

To be able to use this, we need to figure out how to store the counter in memory. The simplest way to represent the state of the counter is to use a pair of numbers $(v, t_0)$, where $t_0$ is the time of the last update, and $v$ is the amount of matter at that time. In this case, the update rule and estimation may be written as follows:

$ \begin{align*} (v, t_0) &\mathop{\mapsto}^t (v \alpha^{-(t - t_0)} + 1, t) \\ r((v, t_0), t) &= v \alpha^{-(t - t_0)}. \end{align*} $



In the article [1] we take a detailed look at such counters. An important idea that is relevant to mention here is a lower cost representation of the counter state as a single number $s$, the so-called absolute value, which holds all the information needed to work with the counter.
The value of $v$ is not explicitly stored in memory but can be computed at any time. Instead, the value $s$ is stored, such that at time $t$ the value $v$ is expressed as follows:

$ v = \alpha^{s-t}. $



Without going into detail, let us just say that with this approach, the update rule and estimation take the form:

$ \begin{align*} s &\mathop{\mapsto}^t t+\log_\alpha(1 + \alpha^{s - t}) \hspace{10em}(1)\\ r(s, t) &= \alpha^{s - t}.\nonumber \end{align*} $



1.3   QDecay: a Faster Decay


When looking at the exponential decay model, we can see that the decay function (in this case, the exponent) satisfies the differential equation:

$\frac{dv}{dt} = -\lambda v.$


In fact, from a physical point of view, it is instead the other way around: this is the equation describing radioactive decay, and the exponent is its solution.

Indeed, the meaning of the equation is that the rate of decay is proportional to the amount of matter available. At some point, we intended to improve the model making decay faster, so we tried to take a quadratic law (QDecay) instead of a linear one:

$\frac{dv}{dt} = -\lambda v^2.$


The solution is a new decay function:

$ v(t) = \frac{1}{\lambda t + 1/v_0}, $


and it is really gotten steeper.

As a matter of fact…
It is hardly correct to say that a hyperbola is steeper than an exponent. However, large values decay indeed faster (and vice versa for small values).

Similar to the model discussed previously (with exponential decay), here, we can represent the counter state as a single number $s$. The corresponding update rule and rate estimate look like this:

$ \begin{align*} s &\mathop{\mapsto}^t t - \frac{t-s}{1 + \lambda(t - s)} \hspace{10em}(2) \\ r(s, t) &= \frac{1}{\lambda(t - s)}.\nonumber \end{align*} $



The great thing here is that calculating the update function is cheap: it requires only elementary arithmetic operations, with only one division. That is, all we originally wanted was a faster horse (faster decay), but we got a new useful feature (cheaper calculations).

We could go further by providing a higher degree in the equation defining the decay function: $dv = -\lambda v^3 dt,$ and so on, but the solution is more complicated, the calculations are more expensive, and the obvious benefit is somehow not noticeable. Rejected

1.4   SW: Averaging of Interpacket Interval


Consider another approach to constructing counters, namely averaging. In this case, we will average the time interval between neighboring events. We call this value the interpacket interval, because we deal with network traffic, where the event is the arrival of a network packet, and the word “inter-event” has somehow not caught on.

Generally speaking, the point of this approach is that we have a sequence of values of some quantity (in this case, interpacket intervals) that changes too quickly to be used directly, and we want to smooth or average this sequence in some way.

Averaging is…
Let there be a sequence $\langle p_n\rangle$, then its average at the $n$th step is defined as follows:

$ \overline{p}_n = \frac{1}{n} \sum_{i = 1}^n p_i. $


Here, we get the arithmetic mean of the last $n$ members of the sequence.

This definition may be generalized. The weighted average of a sequence $\langle p_n\rangle$ is the sum

$ \sum_{i = 1}^n \omega_i p_i, $


where $\omega_i$ are some weights such that $\omega_i\ge 0, \sum_{i}\omega_i=1$.


Recall that the newer events are, the more interesting we find their contribution to the rate estimate. So it is natural to use weighted averaging instead of usual averaging, giving more weight to recent events. Weights may be chosen in different ways; now, let us try to take the weights as terms of a geometric progression. This way of summing up is called exponential moving average (EMA).

EMA averaging is…
The exponential moving average of the $\langle p_n\rangle$ sequence is defined as follows:

$ \overline{p}^{EMA}_n = \frac{1}{B}\sum_{i = 1}^n (1-\beta)^{n-i} p_i, $


where $\beta\in(0,1)$ is a parameter, $B=\sum_{i = 1}^n (1-\beta)^{n-i}$.

Since there are very many events, i.e., $n$ is large, we may assume that there were some dummy events $p_i$, $i<0$ in the dim and distant past, whose contributions are taken with negligible weights $q^{n-i}$. Then it is more convenient to rewrite the definition as follows:

$ \overline{p}^{EMA}_n = \beta\sum_{i = -\infty}^n (1-\beta)^{n-i} p_i, $


since in this case $B=\sum_{i = -\infty}^n (1-\beta)^{n-i} = 1/\beta$.

One important advantage of EMA over other averaging methods is the ability to collapse a cumbersome sum into a recursive expression:

$ \overline{p}^{EMA}_n = \beta\cdot p_n + (1-\beta)\cdot \overline{p}^{EMA}_{n-1}. $


Thus, it is not necessary to store many old values of $p_n$ for the calculations. By the way, it is the formula (3) is often taken as the definition of EMA [2].

Applying the exponential averaging formula to the interpacket intervals, we get:

$ v_n = \beta\cdot (t_n-t_{n-1}) + (1-\beta)\cdot v_{n-1}, $


where $v_n$ is the desired EMA-averaged interpacket interval, $t_n$ is the moment when the $n$th event occurs.

This model is mentioned again in Section 4.3, where, in particular, we show how to express the counter state by a single number and simplify the calculations. For now, let us just write out the result.

Update the counter when an event occurs at time $t$:

$ \begin{equation*} s \mathop{\mapsto}^t t + \beta\cdot(s-t).\hspace{10em}(4) \end{equation*} $



The reciprocal of the averaged interpacket interval serves as the rate estimate:

$ r(s,t) = -\frac{\beta}{1-\beta}\cdot\frac{1}{s-t}. $



Remark
Using EMA averaging, we can also obtain a model exactly coinciding with the decay model from Section 1.2. Instead of averaging the interpacket intervals, this deals with the value $p_t$, which could be called the momentary rate:

$ p_t = \left\{ \begin{array}{ll}1, & \mbox{if at the moment t an event occurred},\\ 0, & \mbox{otherwise}. \end{array} \right. $



1.5   Probabilistic Counters


The idea of probabilistic counters is to change the counter state when an event arrives, not always, but with some probability. This probability may be defined in various ways, e.g.

  • stay constant (binomial counters);
  • decrease by a factor of 2 after each successful update (Morris counters);
  • change after every $X > 1$ of successful updates.

Probability counters make very efficient use of memory. For example, the original 8-bit Morris counters may be used to account for up to $2^{256}$ events. Their obvious disadvantage, however, is significant inaccuracy in estimating the number of events. We discuss such counters in detail in the article [7], and we also propose some extensions of known algorithms.

2   The Idea of the U-model


If we look at the counters based on the idea of decay, we may notice this peculiarity: the state is described by a pair of numbers $(v, t)$, but then it miraculously appears to be possible to express the state by a single number $s$. Let us try to find a general principle by which this becomes possible for any counters of this type.

Let us temporarily forget the fact that in practice, the counter value must be discrete and represented by a relatively small number of bits, and, staying within the spherical cow concept, let us assume both the counter value and the event arrival time be real numbers, and the transformations over them also are real-valued functions. Later (see Section 3.3) we will learn how to discretize the models, making them usable in practice.

2.1   An Invariant of Decay


Consider a section of the decay curve (see Fig. 1a). Let at time $t_0$ an event was registered, and then on the interval $[t_0, t)$ there were no other events. Now we are at the point $t$ going to account for a new event, or just to see what the value of $v$ is, in order to estimate the rate. One may notice that from the point of view of an observer at the moment $t$ there is absolutely no difference whether the last event occurred at the $(t_0, v_0)$ point on the plot or at $(t'_0, v'_0)$. This fact seems to hint that storing two numbers as the counter state is redundant. Thus, the two formally different versions of reality are functionally equipotent. That is, they give the same effect:

$ (t_0,v_0) \sim (t'_0, v'_0). $


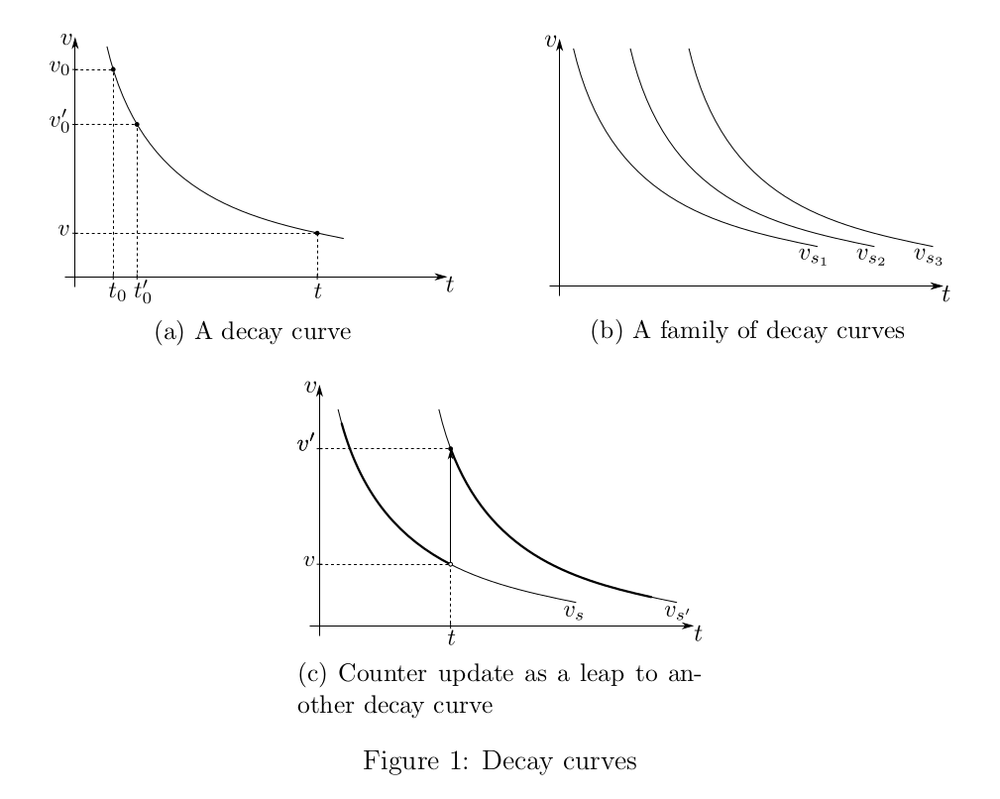
decay curves
Generally speaking, we do not have a single decay curve, but a family $v=v_s(t)$ (see Figure 1b). Each of these curves describes a state of the counter. They may be enumerated somehow, and we may take the index of the curve as the counter state.

Let us now see how such a counter should be updated. Let $s$ be the current state of the counter. According to the decay model, this means that in the absence of events, the value of $v$ changes over time, remaining on the curve $v_s(t)$. Let an event occur at some point $t$. This means that the value of $v$ increases stepwise by one (see Fig. 1c), that is, among the whole family of curves we must find the one that passes through the point $(t, v')$ where $v'=v+1$. Let $s'$ be the index of the found curve, i.e.,

$ \begin{equation*} v_{s'}(t) = v_s(t) + 1,\hspace{10em}(5) \end{equation*} $


then this is the value of $s'$ to set as the new counter state.

Remark
If one wants to count weighted events, the stepwise change should be not by one but by the weight of the event: $v'=v+w$.

It is not yet clear how to find the index of the desired curve, but it will come to light very soon.

2.2   Translational Symmetry


In Fig. 1b decay curves $v_s(t)$ are depicted in such a way that they differ from each other only by a horizontal shift. Scientifically, this is called translational symmetry of the time [8]. We want to take this property as an axiom for our counter model. Indeed, it is logical to expect that, within the model, the decay process goes today in exactly the same manner as it did yesterday.

Mathematically, this property may be written as follows:

$ \forall t\in\mathbb{R}\colon v_{s_2}(t) = v_{s_1}(t-\Delta), $


that is, the curve $v_{s_2}(t)$ is obtained from the curve $v_{s_1}(t)$ by shifting it to the right by some $\Delta$.

In general, curves may be enumerated any way you like, and you just need to be able to find the index of the new curve during the update operation. But it is more convenient to enumerate them in order so that the index $s$ represents something meaningful, namely, a real number corresponding to the horizontal distance between the $v_s(t)$ curve and the curve with zero index $v_0(t)$. Then, due to translational symmetry, any curve from the family may be very simply expressed as a shift of the curve number zero:

$ \begin{equation*} \forall t,s\in\mathbb{R}\colon v_s(t) = v_0(t-s)\equiv \mu(s-t).\hspace{10em}(6) \end{equation*} $


Remark
Here we introduce the notation $\mu(x) := v_0(-x)$, which is convenient because the function $\mu$ increases monotonically. This will come in handy later in Section 2.4 in determining the rate.

Now, the update rule on an event arrival at time $t$ may be expressed from equation (5) as follows:

$ \begin{align*} &s' = t + u(s-t),&\\ &\quad \text{where } u(x) = \mu^{-1}(\mu(x) + 1).&\hspace{10em}(7) \end{align*} $



Thus, the update rule appears as

$ \begin{equation*} s \mathop{\mapsto}^t t + u(s-t),\hspace{10em}(8) \end{equation*} $


where $u(\cdot)$ is some function.

This rule looks so simple and universal that it may be taken as the definition. That is how we will define the u-model.

Remark
If the decay function is given by a differential equation of such kind:

$ \frac{dv}{dt} = f(v), $


then it is always easy to find an invariant for that the property (6) holds.

Indeed, the solution of the differential equation may be written as

$ F(v) - F(v_0) = t - t_0,\quad\mbox{where } F(v) = \int \frac{dv}{f(v)}. $


Thus we can take $s = t_0-F(v_0)$ as an invariant, and the corresponding curve is expressed as $v_s(t)=F^{-1}(t-s)$.

Section 3.1 lists the formal properties that the function $u$ must satisfy in order to build a workable counter model on its basis.

2.3   Absolute and Relative


We may say that $s$ is the absolute value of the counter, it is stored directly in memory, and $x=s-t$ is the relative value of the counter at time $t$. Then it turns out that the update function works with the relative counter value: $x' = u(x)$.

The fact that the update function works with the relative counter value reflects the decay principle: if no events occur, then the absolute value of $s$ does not change, and the relative value automatically decreases over time. And the rate estimate, accordingly, also degrades. From the calculation point of view, it is very convenient: as long as there are no events, there is no need to do anything. It is very similar to inflation in economics: the state of the counter stands for banknotes lying under the pillow, and the rate estimate stands for the purchasing power of these banknotes, which degrade itself.

2.4   Rate Estimate


For the decay model, the value $\mu(s-t)$ by construction is the rate estimate, see formula (6). However, several problems arise with this definition. First, if we use the definition of the model through the function $u$, it would be difficult to construct the function $\mu$ (the functional equation (7) would be needed to solve). Secondly, it would be nice to check experimentally how adequately a particular counter measures the rate.

Preserving not the letter (from the formula (6)), but the spirit of the decay idea, we construct the rate estimate as a function of a single argument, namely, the relative value of the counter: $r(s, t) = r(s-t)$. Thus, the problem is set as follows: having an update function $u(x)$, construct a function $r(x)$ that would be an adequate estimator of the rate.

It turns out that the u-model approach consists of implementing the following plan (yes, it looks a bit punkish).

  1. We take some models built from “physical considerations”, and for each of them, we express the update rule through a u-function.
  2. Then we abstract away from the physical sense, leaving only the bare u-function. Now we can, without worrying about the sense, boldly change the u-function, for example, by choosing a computationally cheaper one.
  3. Finally, we figure out how to reintroduce meaning, i.e., to construct an adequate estimate of the rate.
  4. PROFIT!

In order to make this plan possible (the snag, obviously, is only clause 3), some constraints on the u-function would have to be imposed, and now let us try to figure out which ones. The reader, however, may skip these motivational considerations and jump directly to the definition of those constraints (9) on the u-function in Section 3.

2.4.1   A Uniform Stream


Our company studies network traffic, and we may need to count network packets arrivals as items. In this case, they form a stream, and its rate is measured in packets per second (pps). Alternatively, we have to take packet size into account, so the size is considered the weight of an event, and correspondingly, the rate of such a weighted stream is measured in bits per second (bps). It may also be important to distinguish packets by their contents (source and/or destination IP address, port number, protocol, etc.), then we group events by their type and create separate counters for each type.

Since we discuss here how to evaluate the rate of an event flow, we must first formalize the notions of the event and the event stream.

Definition (event). Let us call an event a triple $(id, w, t)$, where $t$ is the event arrival time, $w>0$ is the event weight, $id$ is the event type, some stream identifier.

Definition (event stream). An event stream is defined as a sequence of events $\mathcal{E}_k=(id_k,w_k,t_k)$, $k\in\mathbb{Z}$. And the events in the stream must be ordered by time: $t_i\le t_j$ at $i<j$.


In most implementations of event accounting systems, the time is considered a discrete value: $t_k\in\mathbb{Z}$, but for theoretical reasoning, it may be convenient to generalize and consider the time continuous: $t_k\in\mathbb{R}$.

If we are interested only in events as such, e.g., we measure the number of packets in pieces per second, then the weight $w$ may be assumed to be unity. It is also assumed that a single counter counts events of the same type, i.e., the $id$ field serves to distinguish different streams and does not play a role within a single counter.

Definition (uniform stream). A deterministic uniform stream $\langle t_k\rangle$ is defined as follows:

$ t_k = pk,\quad k\in\mathbb{Z}, $


Where $p>0$ is the stream parameter, i.e., the period between events. Then the rate of such a stream, by definition, is expressed as $r=1/p$.


Now we can express a way to measure the stream rate for any model. Consider a stream of some known rate $r$ affecting a counter and observe how the relative value of the counter changes; let the measured counter value be $x_n$ after the $n$th event.

We want the stream rate $r$ and the sequence of $x_n$ values to be somehow related. Then, being lucky, we could construct a rate estimation function $r(x)$.

2.4.2   An Attractor


Studying with concrete examples the behavior of the u-model under the influence of a deterministic stream, we found that (at least for those examples) there is a notion of an attractor, which is somewhat informally described by the following properties.

  • For every rate value of the incoming stream $r$, there exists an attractor, i.e., such a subset of the relative counter values that if any value $x_N$ ended up in this attractor, then all subsequent values $x_n$ for $n\ge N$ will also end up there. The attractor is an interval $[\check{x}, \hat{x}]$ (possibly degenerate, when both ends of it have merged).
  • There is convergence: even if the relative value of the counter was outside the attractor, after several updates, it will get there or at least get as close to the attractor as possible.
  • There is monotonicity: the position of the attractor depends monotonically on the rate of the incoming stream. That is, both ends of the segment $\check{x}(r)$ and $\hat{x}(r)$ are monotonically increasing functions.

Since we need to judge the rate of the stream by the value of the counter, we need to solve the inverse problem. This is possible due to monotonicity and continuity: there exist functions $\check{r}(x), \hat{r}(x)$ such that if $x$ enters the attractor, we can guarantee that the true rate value lies in the interval $[\check{r}(x), \hat{r}(x)]$.

Of course, for these properties to be practically useful, first, the segment (attractor) must be short; otherwise, the accuracy will be low, and second, the convergence must be fast, or one will have to wait for a long time before the counter starts to show an adequate value. In any case, for a particular u-model, it is possible to write down the solution explicitly and evaluate the accuracy and speed of convergence.

Let us try to pass from the particular to the general. Now, ask a question: What conditions must be imposed on the u-function for the corresponding u-model to have an attractor with the above properties? An exhaustive answer is given in the next section.

3   Implementation of the U-model


3.1   Definition of the U-model


Let the function $u\colon\mathbb{R}\to\mathbb{R}$ satisfy the following conditions:

$ \begin{align*} &u(x)\text{ increases},&\hspace{10em}(9a)\\ &\Delta u(x) \ge 0\text{ for all }x,&\hspace{10em}(9b)\\ &\Delta u(x)\text{ decreases},&\hspace{10em}(9c)\\ &\Delta u(+\infty)=0,&\hspace{10em}(9d) \end{align*} $


where $\Delta u(x) = u(x)-x$.

Definition (u-model). Consider a counter update method based on the function $u$
having the properties (9), in which the counter update $s$ on
event arrival at time $t\in\mathbb{R}$ is expressed by the rule (8):

$ s\mathop{\mapsto}^t t + u(s-t). $



This way of updating the counter will be called the u-model.


A function $u$ satisfying the conditions (9), has some useful properties. For example, the function $u$ (and also $\Delta u$) is continuous. This arises from the properties (9a) and (9c) having used the $\varepsilon$-$\delta$-formalism. Second, either $\Delta u(x)>0$ on $\mathbb{R}$, or there exists such $x_{max}\in\mathbb{R}$ that $\Delta u(x)>0$ at $x<x_{max}$, and $\Delta u(x)=0$ at $x\ge x_{max}$.

3.2   Rate Measurement


Properties (9) are sufficient to ensure the existence of an attractor and to construct upper $\hat{r}$ and lower $\check{r}$ estimates of the rate. There are several theorems on this point, some of which are presented in this section and some of which are left out.

3.2.1   A Strict U-model


We can observe that the conditions (9) do not forbid the case when the increment of the update function converts to zero at some point, that is, when $\exists x_{zero}\colon \Delta u(x_{zero})=0$. In this case, $\Delta u$ will also convert to zero at all $x>x_{zero}$. Let us denote by

$ \begin{gather*} X = \{x\mid \Delta u(x)>0\}\\ x_{max}=\sup X,\quad x_{max}\in\mathbb{R}\cup\{+\infty\}. \end{gather*} $


It is easy to prove that if we take $x_0\in X$ and apply a series of updates to it, then values larger than $x_{max}$ will be unattainable, so the relative counter values will never go beyond $X$. That is, $X=(-\infty, x_{max})$ may be called the operating range of the u-model. Outside this range, the u-function is arranged trivially, and we are not interested in its behavior. This caveat is needed to introduce the notion of a strict u-model.

Definition (strict u-model). If, in addition to the properties (9) functions $u$ and $\Delta u$ are strictly monotone on $X$, then the corresponding u-model will be called strict.


Theorem (fixed point theorem). For a strict u-model under the influence of a deterministic uniform rate stream $r$, a sequence of values $x_n$ is constant if an additional condition is satisfied: the function $u$ is a compressive mapping, that is, $\exists \kappa\in(0,1)$ such that $\forall a \forall b\colon |u(a) - u(b)| < \kappa|a-b|$.


This directly follows from the Banach fixed-point theorem [5], which guarantees the existence and uniqueness of a fixed point in a compressible mapping. Then all terms of the sequence $x_n$ will be equal to the value of this fixed point.

It turns out that in a strict u-model, the attractor consists of a single point.

In fact, not for all u-models we use the update function is a compressible mapping. For example, the EDecay model has an “almost” compressible update function, as for it, the constant $\kappa$ is equal to one. That means the Banach theorem does not work. But this is not a problem from the practical application point of view because there are other useful theorems.

For example, the following statement holds.
Statement. If at some point in time the counter was in a state where its relative value was $x_0$, and a deterministic stream of events began to arrive at it, then the sequence of its relative values $x_k$ tends to some value of $x^*$, and the convergence rate is known. In particular, for the EDecay model, the convergence looks like this: $|x_k-x^*|\le C\alpha^{-(t_k-t_0)}$, which, from a practical point of view, allows us to evaluate how quickly and adequately the model responds to changes in the traffic pattern.

3.2.2   A Non-strict U-model


As for discretized models (see Section 3.3), they lose strict monotonicity, so instead of the fixed point theorem, a set of assertions (not given here) that require weaker conditions and give weaker, though still useful, results for rate estimation helps. For the non-strict model, instead of a one-to-one correspondence between the rate of the stream and the relative value of the counter, there is an interval estimate. That is, the attractor is a nondegenerate segment.

Using the proposed methodology, for a given u-model, all that remains is to construct upper $\hat{r}$ and lower $\check{r}$ estimates of the rate and find out how rapidly the $x_n$ sequence converges to the attractor.

3.3   Discretization


In order to use the u-model in practice, it must be discretized. That is, to make the set of counter states finite and preferably small in size. Why small? We need to keep billions of counters in memory; the more of them, the higher will be the quality of service. Indeed, why should we waste 64 bits per counter when we can do with 16?

Remark
One may go for the trick of complicating the state representation by assuming it as a pair $s=(s_{local}, s_{global})$, where $s_{local}$ refers to a particular counter, and $s_{global}$ is the common part of the state of a whole group of counters. We do use this technique, in particular, to deal with counter overflows, but we do not consider it in this paper.


One obvious way to discretize is to select a finite subset of consecutive integers from the continuum of relative counter values and modify the u-function slightly to become an integer.

First, let us construct a function $u^\sqcup\colon \mathbb{R}\to\mathbb{R}$ such that:

  • it has integer values at integer points: $u^\sqcup(n) \in \mathbb{Z}$ for $n\in\mathbb{Z}$,
  • is in some sense close to $u$: $u^\sqcup(n)\approx u(n)$ for $n\in\mathbb{Z}$,
  • satisfies the conditions (9).

Apparently, this problem may be solved in different ways. Below is one particular way of constructing $u^\sqcup$.

The basic idea of this construction is to set the values of $u^\sqcup$ at integer points by rounding down, that is, $u^\sqcup(n):=\lfloor u(n)\rfloor$ for $n\in\mathbb{Z}$, then complete $u^\sqcup$ at intermediate points so that continuity and monotonicity (conditions (9)).

It is more convenient to first construct $\Delta u^\sqcup$ and then determine $u^\sqcup$ through it. To do this, fix $\Delta u^\sqcup$ at integer points, and do linear interpolation at intermediate points. That may be written as follows:

$ \Delta u^\sqcup(x) = (1-\varepsilon)\Delta u(n) + \varepsilon\Delta u(n+1), $


where $n=\lfloor x\rfloor,$$\varepsilon = \{x\}$ are the integer and fractional parts of the argument, respectively.

All that remains is to determine the function $u^\sqcup(x)$ itself:

$ u^\sqcup(x) = \Delta u^\sqcup(x) + x. $



Statement. The function $u^\sqcup$ thus constructed satisfies the conditions (9) and thus defines the u-model.


Remark
Generally speaking, the u-model gets a bit screwed up with this operation (switching from $u$ to $u^\sqcup$): if it was strict, it ceases to be so after the transformation.


A legitimate question arises: why do we need to add $u^\sqcup$ at intermediate (non-integer) points if we plan to perform calculations only over integer counter values? The point is that in addition to the update rule, we need to build another rate estimate, and the easiest way to do that is to apply a “lazy approach”: first, extend $u^\sqcup$ at non-integer points, gaining a new u-model, then use theorems relating the observed counter value to rate estimates, thus reducing the problem to the solved one.
Remark
There seems to be some meta theorem to claim that, regardless of the way $u^\sqcup$ is constructed at intermediate points, the methodology for constructing the estimates gives the same result.


Now we have a function $u^\sqcup$ that generates a u-model and takes integer values at integer points. It remains to take care of limiting it on a finite interval, so that the counter values do not spread to infinity. To do this, take the integer interval $X^\square=\{x_{min},\dots, x_{max}\}$ and limit $u^\sqcup$ on it, that is, we get a function $u^\square\colon X^\square\to X^\square$ that matches $u^\sqcup$ on the area of definition.

How to choose the interval bounds
Take as $x_{max}$ such a number that $\Delta u^\square(x_{max})=0$, $\Delta u^\square(x_{max}-1)>0$. (By virtue of the condition (9d), such a number exists.) Then the result of the update will never exceed the right bound: for $\forall x\in X^\square$ we have $u^\square(x)\le x_{max}$. As for the left boundary, it may be chosen arbitrarily (any $x_{min} < x_{max}$ will do). Indeed, due to non-negativity of $\Delta u^\square$ for $\forall x\in X^\square$, $u^\square(x)\ge x \ge x_{min}$ will be satisfied, that is, the result of the update will not exceed the left boundary. Thus, $x_{min}$ may be chosen based on counter size considerations: the larger the counter capacity, the more left-hand boundary may be moved, and the more accurate the estimate of low-intensity streams will be.


It is this function $u^\square$ (more precisely, its numerical implementation) that we will use in the counter update algorithm.

Section B of the Appendix shows the discretization of the EDecay model as an example.

4   Examples of U-model Counters


As shown above, the counters introduced in Section 1 (except for linear ones) are represented as u-models. Here we consider them again, now as u-models: first, take the u-function, then construct the estimators.

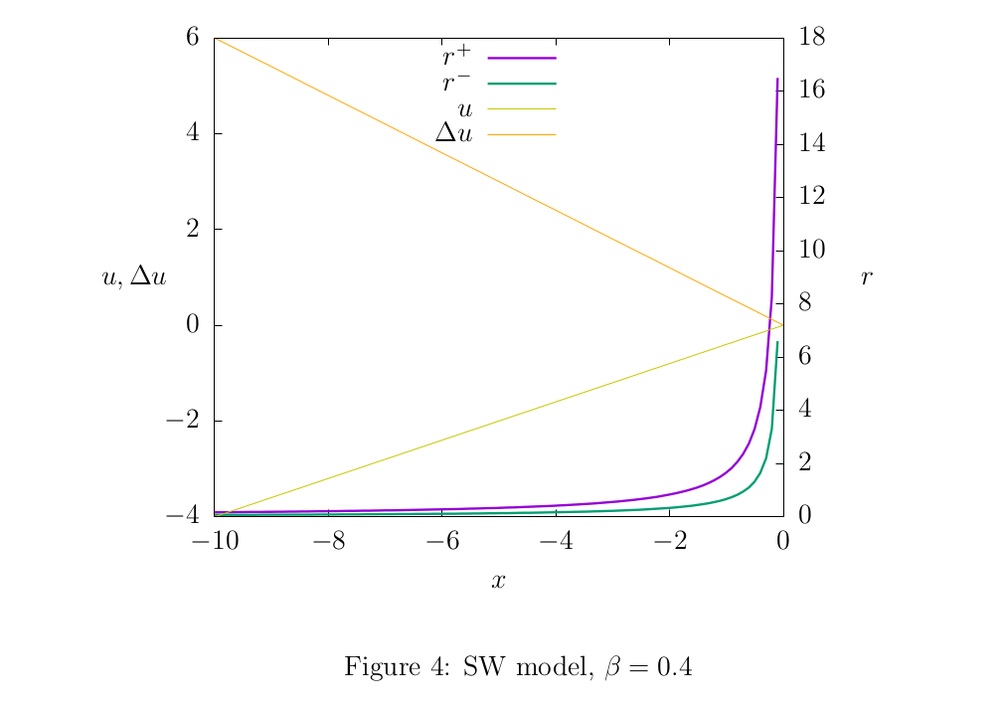
Figures 2,3, and 4 illustrate the properties of the models: shades of yellow show the function graphs $u(x)$ and $\Delta u(x)$, and the remaining graphs are rate estimates. The parameters of the models were chosen in such a way as to show the difference between the upper and lower estimates. In practice, we use such parameter values so that the estimates are more accurate. If, for example, for the EDecay model we take $\tau$ larger (for example, in our working code $\tau$ is about $10^8$), the graphs of the estimates will visually merge, which obviously indicates the high accuracy of the model.

4.1   EDecay


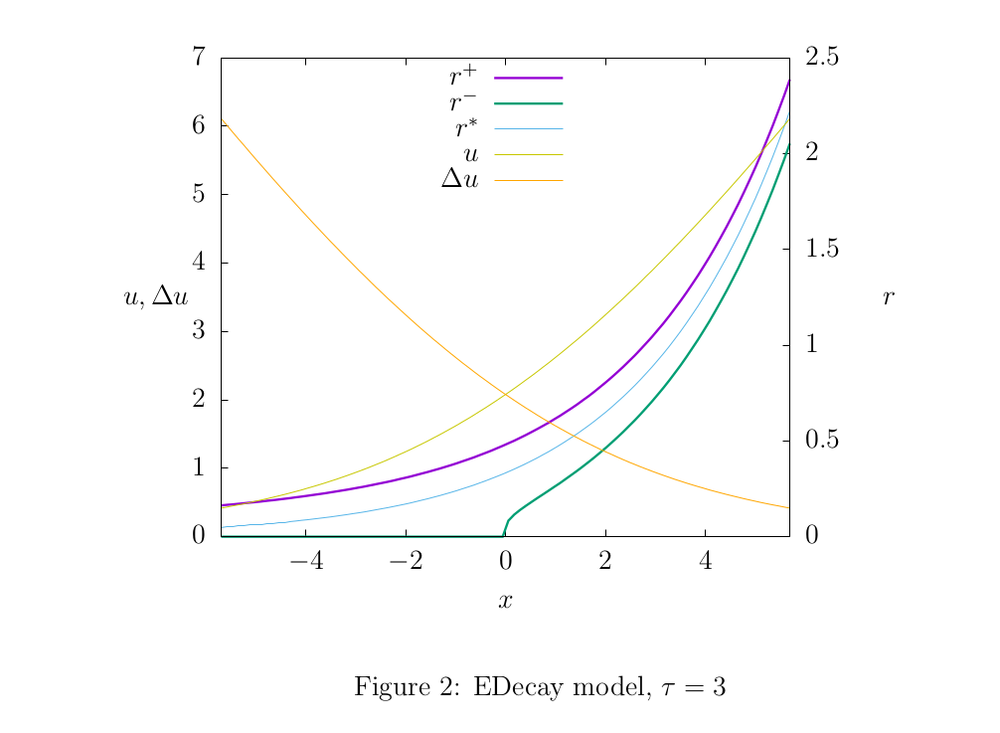
EDecay
The update rule (1) looks like this:

$u(x) = \log_\alpha(1+\alpha^x),$


where $\alpha>0$ is a parameter (see Section A of the Appendix).

This model has an interesting feature: there is an estimating function $r^*(x) = \alpha^x$ (its graph is indicated by the blue line in Fig. 2), which has the following property. Let there be two counters that account for two different event streams and a third counter that accounts for both streams at once. Then for the EDecay model, there exists an estimator function $r^*(x)$ such that at each time $t$ the equality holds:

$r^*(s_1-t) + r^*(s_2-t) = r^*(s-t),$


where $s_1$ and $s_2$ are the absolute value of the first two counters, and $s$ is the absolute value of the third. It makes sense to call this property of the model additivity. It turns out that EDecay is the only one among all u-models that has this property. For other u-models, this equality can be satisfied only approximately. Here, by the way, there is a clear analogy with radioactive decay: we may say that this estimate $r^*(x)$ plays the role of mass or amount of matter.

4.2   QDecay


The corresponding rule (2) the update function looks like this:

$u(x) = \frac{x}{1-x/\tau}.$


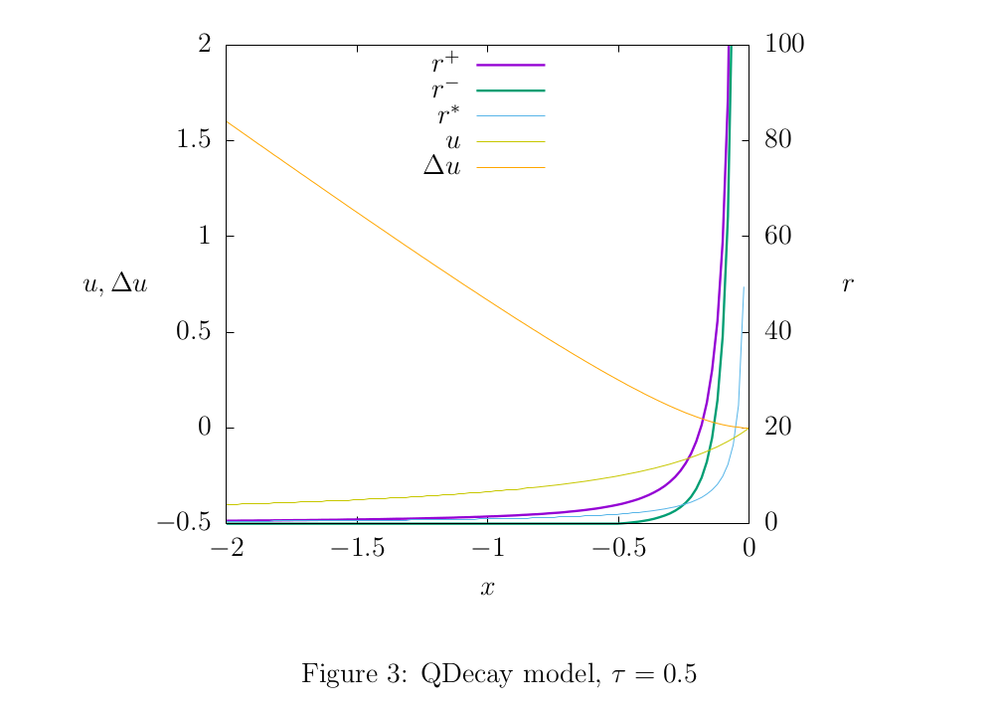
QDecay

4.3   SW


The update rule (4) is equivalent within the u-model through the update function

$u(x) = \beta x.$


A useful property of this model is the computational simplicity of the update function; we can directly write this formula into code without any table approximations.

SW

4.4   Summary Table


Table 1 lists the characteristics of the mentioned models.

summary table
One may notice that for some models, the formula for the lower estimate $r^-$ becomes meaningless at some values of the argument. That means that for such (too small) relative counter values, we cannot say anything about how small the rate may be, so we assume that the lower estimate simply equals zero (no rate is less than zero). Theoretically, for some u-models, it may happen that the upper estimate $r^+$ makes no sense for some reason. In such cases, it should be assumed to be infinite.

In addition to the rigorous rate estimates $r^-$ and $r^+$ derived from the general u-model methodology, an estimate of $r^*$ constructed “from physical considerations” (the blue line in the graphs) is also indicated. It was expected that it would always be between the lower and upper estimates ($r^-$ and $r^+$), but with the QDecay model, this is not the case, as there is an area where it is smaller than the lower estimate. This example shows the usefulness of the approach described here: whatever the considerations on which the counter model is built, it is always useful to double-check how a stream of a known rate affects the state of the counter.

Conclusions


The general principles of event counters have been shown in several examples. As a rather universal generalization, the u-model scheme has been proposed. A methodology for constructing rate estimates for any u-model has been proposed.

In addition, a lot of interesting things were left out of the picture.

  • Probability Counters. What happens if we replace the $u$ function in the u-model update rule with a random variable that depends on the relative value of the counter?
  • Representation and maintenance of large arrays of identical counters. The update and evaluation functions depend on the relative counter value $x=s-t$, where $s$ and $x$ may be in a relatively narrow range of values, while $t$ runs over a wide (potentially infinite) range. How can we make sure that the counters do not overflow?
  • Algorithms detecting heavy streams. Individual counters allow us to measure the rate of streams, but how do we organize them to reveal the most intense streams?

Appendix


A   Parameterization


All of the counter models discussed in this article are single-parameter. But we use different values in different places to make the formulas look more convenient. Below is a list of quantities that may be equally used as a model parameter, with an indication of their physical meaning and the relationship between them.

  • $\lambda>0$ is the so-called decay constant from the law of radioactive decay [4]

    $v(t) = v_o e^{-\lambda t}.$

  • $\tau>0$, $\tau=1/\lambda$ is a value characterizing the average lifetime in the same model. It is also true that during the time $\tau$ the amount of decaying matter decreases $e$ times, and the half-life is expressed through $\tau$ as follows: $T_{1/2}=\tau\ln2$.
  • $\alpha>1$, $\alpha=e^\lambda$.
  • $\beta\in(0,1)$ is the smoothing parameter in the EMA [2]

    $v_n = \beta\cdot (t_n-t_{n-1}) + (1-\beta)\cdot v_{n-1}.$


    The exponential decay model may be expressed in two ways: through radioactive decay and through EMA smoothing. Here is the relationship between these parameters: $\beta = 1-1/\alpha$.

B   An Example of EDecay Discretization


The EDecay model is defined by the following update function:

$ u(x) = \log_\alpha(1 + \alpha^x). $


Consider in Fig. 5 how the update function changes with sampling.
interpolated EDecay
  1. There is a perfect real-valued update function that exactly exponential decay model (the smooth green line in the graph).
  2. It has to be discretized for practical applications. It is possible to use a floating-point representation (obviously, it is also discretized, only not uniform) or take an integer representation. In this case, rounding down applies, although it is not crucial (blue line).
  3. Finally, It is possible to overload the update function even more. In [1] to speed up calculations, it was suggested that instead of calculating the real-valued function with logarithms and exponents, a table approach should be used. It was assumed that the size of the table would be small if a low-digit counter was used. However, nothing prevents us from thinning the table by reducing its size a few more times and implementing linear interpolation. The resulting update function will be slightly different (the red dotted line on the graph).

Of course, as a result of sampling, the update function is distorted, which is not a problem in itself, but we have to take it into account when constructing the rate estimate. In addition, strict monotonicity of the model is inevitably lost, which reduces the accuracy of the estimate. The degree of distortion depends on the parameter $\tau$: the larger it is, the closer the discretized function is to the original one.

References


[1] Our article about the decay model: https://qratorlabs.medium.com/rate-detector-21d12567d0b5
[2] Exponential moving average: https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average
[3] Weighted moving average: https://en.wikipedia.org/wiki/Moving_average#Weighted_moving_average
[4] The radioactive decay law: https://en.wikipedia.org/wiki/Exponential_decay
[5] Banach fixed-point theorem: https://en.wikipedia.org/wiki/Banach_fixed-point_theorem
[6] Ayur Datar et al. — Maintaining Stream Statistics Over Sliding Windows — Society for Industrial and Applied Mathematics, Vol. 31, No. 6: http://www-cs-students.stanford.edu/~datar/papers/sicomp_streams.pdf
[7] Our overview of Morris's counters: https://habr.com/ru/company/qrator/blog/559858/
[8] Translational symmetry: https://en.wikipedia.org/wiki/Translational_symmetry

Комментарии (2)