Я работаю программистом в игровой студии IT Territory, а с недавних пор перешел на направление экспериментальных проектов, где мы проверяем на прототипах различные геймплейные гипотезы. И работая над одним из прототипов мы столкнулись с задачей генерации случайных чисел. Я хотел бы поделиться с вами полученным опытом: расскажу о псевдогенераторах случайных чисел, об альтернативе в виде хеш-функции, покажу, как её можно оптимизировать, и опишу комбинированные подходы, которые мы применяли в проекте.

Случайными числами пользовались с самого зарождения математики. Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях. 

Есть разные способы получения случайных чисел. Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди. 

К первым техническим способам получения случайных чисел можно отнести различные генераторы с использованием энтропии. Это устройства, основанные на физических свойствах, например, емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.

Сегодня мы с вами поговорим о генераторах псевдослучайных чисел — вычисляемых функциях. К ним предъявляются следующие требования:

• Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.

• Портируемость алгоритма на различные системы. 

• Скорость получения последовательности. Чем быстрее, тем лучше. 

• Повторяемость результата. Это очень важный показатель. От него зависят все компьютерные игры, которые используют генераторы миров и различные системы с аналогичной функциональностью. Воспроизводимость даёт нам общий контент для всех, то есть мы можем генерировать на отдельных клиентах одинаковое содержимое. Также мы можем генерировать контент на лету в зависимости от входных данных, например, от местоположения игрока в мире. Ещё повторяемость случайных чисел используется для сохранения конкретного контента в виде зерна. То есть мы можем держать у себя только какое-то число или массив чисел, на основе которых будут генерироваться нужные нам параметры для заранее отобранного контента.

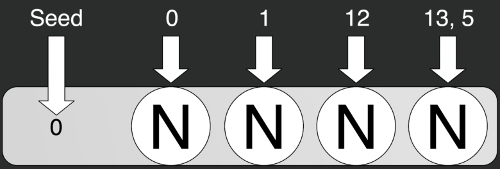
Зерно

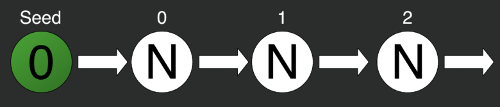
Зерно — это основа генерирования. Оно представляет собой число или вектор чисел, который мы отправляем при инициализации генератора. 

var random = new Random(0);
var rn0 = random.Next();
var rn1 = random.Next();
var rn2 = random.Next();

На иллюстрации просто инициализирован стандартный генератор случайных чисел из стандартной библиотеки C#. При инициализации отправляем в него некоторое число — seed (зерно), — в данном случае это 0. Затем по очереди берём по одному числу методом Next. Но тут мы столкнёмся с первой проблемой: генерирование всегда будет последовательным. Мы не можем получить сразу i-тый элемент последовательности. Для получения второго элемента последовательности необходимо сначала задать зерно, потом вычислить нулевой элемент, за ним первый и только потом уже второй, третий и i-й. 

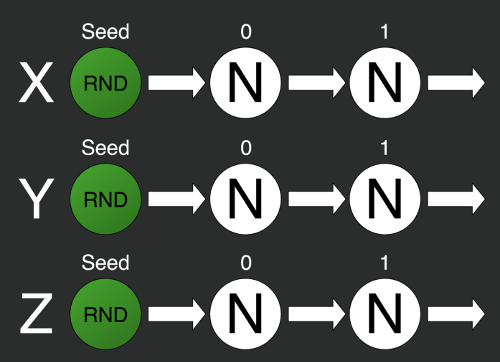
Решить эту проблему можно будет с помощью разделения одного генератора на несколько отдельных. 

var X = 0;
var Y = 1;
var Z = 2;

var rs0 = new Random(X);
var rs1 = new Random(Y);
var rs2 = new Random(Z);

То есть берём несколько генераторов и задаём им разные зёрна. Но тут мы можем столкнуться со второй проблемой: нельзя гарантировать случайность i-тых элементов разных последовательностей с разными зёрнами. 

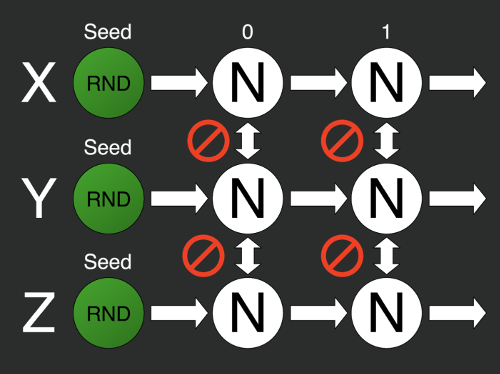
На иллюстрации изображён результат генерирования нулевого элемента последовательности с помощью стандартной библиотекой C#. Мы постепенно меняли зерно от 0 до N. 

Качество генератора

Предлагаю оценивать качество генератора с помощью изображений разного типа. Первый тип — это просто сгенерированная последовательность, который мы визуализируем с помощью первых трёх байтов полученного числа, конвертированных в RGB-представление. 

private static uint GetBytePart(uint i, int byteIndex)
{
   return ((i >> (8 * byteIndex)) % 256 + 256) % 256;
}

public static Color GetColor(uint i)
{
   float r = GetBytePart(i, 0) / 255f;
   float g = GetBytePart(i, 1) / 255f;
   float b = GetBytePart(i, 2) / 255f;
   return new Color(r, g, b);
}

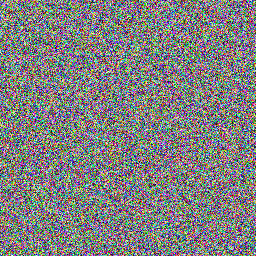
Второй тип изображений — это пространственная интерпретация сгенерированной последовательности. Мы берём первые два бита числа (Х и Y), затем считаем количество попаданий в заданные точки и при визуализации вычитаем из 1 отношение количества попаданий в конкретный пиксель к максимальному количеству попаданий в какой-то другой пиксель. Черные пиксели — это точка, куда мы попадаем чаще всего, а белые — куда мы либо почти, либо совсем не попали. 

var max = 0;
for (var i = 0; i < ints.Length; i += 2)
{
   var x = GetBytePart(ints[i], ByteIndex);
   var y = GetBytePart(ints[i + 1], ByteIndex);
   var value = coords[x, y];
   value++;
   max = Mathf.Max(value, max);
   coords[x, y] = value;
}

Сравнение генераторов

Стандартные средства C#

Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом. 

В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности. 

Линейный конгруэнтный генератор (LCG)

Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом. 

const long randMax = 4294967296;
state = 214013 * state + 2531011;
state ^= state >> 15;
return (uint) (state % randMax);

При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu. 

const long randMax = 2147483648;
state = 65539 * state + 0;
return (uint) (state % randMax);

Этот генератор страшен тем, что умножает одно большое число на другое и берёт остаток от деления на 2³¹. В результате формируется вот такая красивая картинка. 

XorShift

Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.

state ^= state << 13;
state ^= state >> 17;
state ^= state << 5;
return state;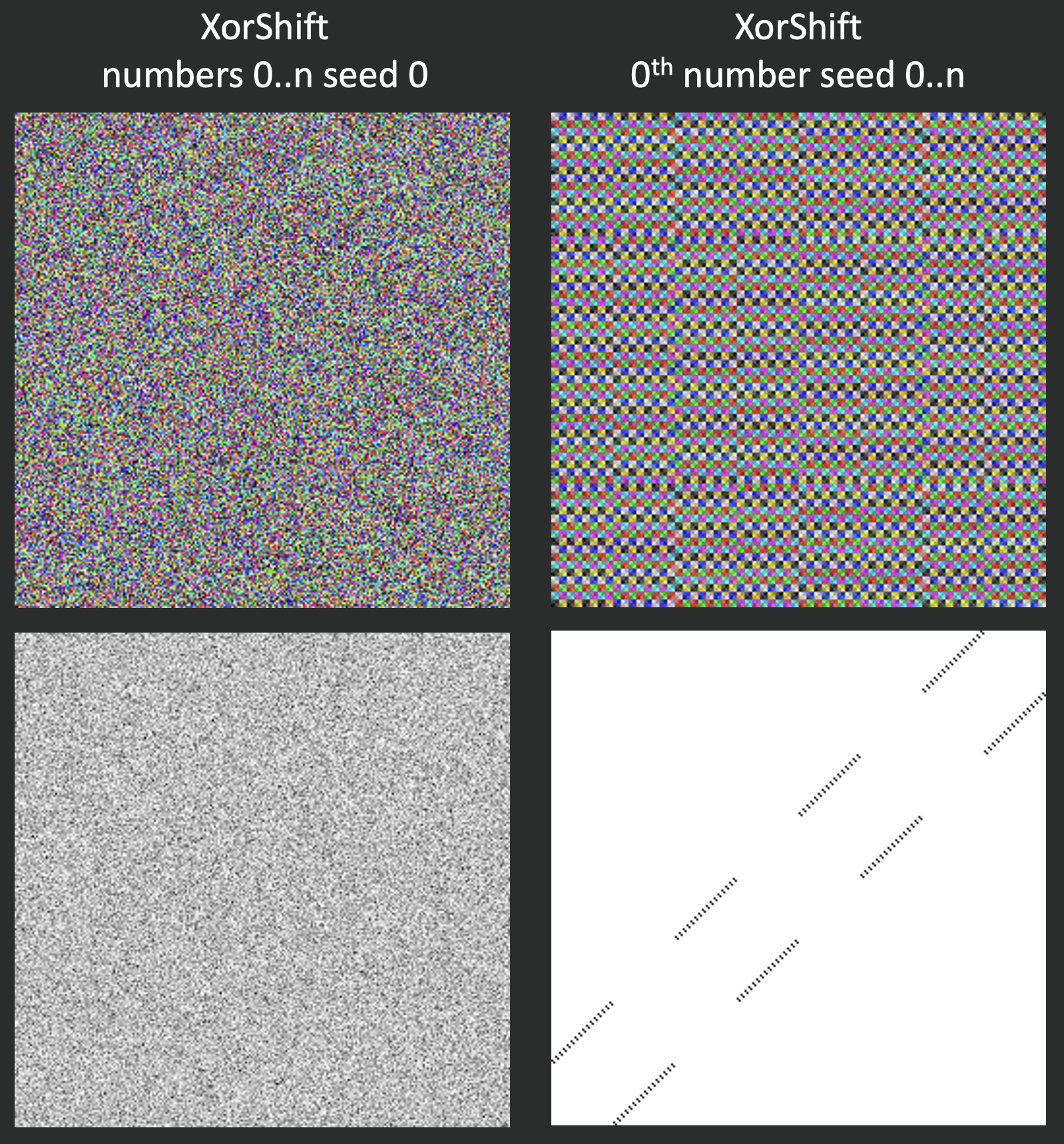

Вихрь Мерсенна

Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.

ulong x;
 if (mti >= NN)
 {
  // generate NN words at one time
  for (var i = 0; i < NN - MM; i++)
  {
   x = (mt[i] & UM) | (mt[i + 1] & LM);
   mt[i] = mt[i + MM] 
           ^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
  }
  for (var i = NN - MM; i < NN - 1; i++)
  {
   x = (mt[i] & UM) | (mt[i + 1] & LM);
   mt[i] = mt[i + (MM - NN)] 
           ^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
  }
  x = (mt[NN - 1] & UM) | (mt[0] & LM);
  mt[NN - 1] = mt[MM - 1] 
               ^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
  mti = 0;
 }
 x = mt[mti++];
 x ^= (x >> 29) & 0x5555555555555555L;
 x ^= (x << 17) & 0x71d67fffeda60000L;
 x ^= (x << 37) & 0xfff7eee000000000L;
 x ^= x >> 43;
 return x;

Unity — Random

Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность. 

Перемешанный конгруэнтный генератор (PCG)

Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.

Длительность последовательного генерирования

Это важная характеристика генераторов. В таблице приведена длительность для алгоритмов в миллисекундах. Замеры проводились на моём MacBook Pro 2019 года. 

Вихрь Мерсенна работает дольше всего, но даёт качественный результат. Стандартный генератор Random из библиотеки C# подходит для задач, в которых случайность вторична и не имеет какой-то значимой роли, то есть его можно использовать в рамках одного зерна. LCG (линейный конгруэнтный генератор) — это уже более серьёзный алгоритм, но требуется время на подбор нужных коэффициентов, чтобы получить адекватный паттерн. XorShift — самый быстрый алгоритм из всех рассмотренных. Его можно использовать там, где нужно быстро получить случайное значение, но помните про ярко выраженный паттерн с повторяющимся значением. Unity Random и PCG (перемешанный конгруэнтный генератор) сопоставимы по длительности работы, поэтому в разных ситуациях мы можем менять их местами: для длительных последовательностей использовать Unity, а для коротких — PCG.

Альтернатива генераторам — хеш-функции

Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.

Требования к генераторам на основе хеш-функций предъявляются те же самые, что и к простым генераторам, кроме длительности получения последовательности. Дело в том, что такому генератору можно отправить на вход одновременно зерно и требуемое состояние, потому что хеш-функции принимают на вход массивы данных. 

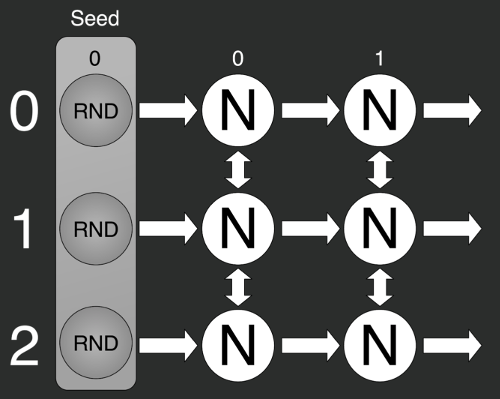
Вот пример использования хеш-функции: можно либо создать конкретный класс, отправить туда зерно и постепенно запрашивать только конкретные состояния, либо написать статичную функцию, и отправить туда сразу и зерно, и конкретное состояние. Слева показан алгоритм работы MD5 из стандартной библиотеки C#. 

var hash = new Hash(0);
var rn0 = hash.GetHash(0);
var rn1 = hash.GetHash(1);
var rn2 = hash.GetHash(12);
var rn3 = hash.GetHash(13, 5);

var rn4 = Hash.GetHash(0, 0);
var rn5 = Hash.GetHash(0, 1);
var rn6 = Hash.GetHash(0, 12);
var rn7 = Hash.GetHash(0, 13, 5);

Сделать генератор на основе хеш-функции можно так. Непосредственно при инициализации генератора задаём зерно, увеличиваем счётчик на 1 при запросе следующего значения и выводим результат хеша по зерну и счётчику. 

class HashRandom
{ 
	private int seed; 
	private int counter;  
	public HashRandom(int seed) 
{  
	this.seed = seed; 
	} 
	public uint Next() 
	{  
	return Hash.GetHash(seed, counter++); 
	}
}

Одни из самых популярных хеш-функций — это MurMur3 и WangHash.

MurMur3 не создаёт паттернов при использованиии i-тых элементов разных последовательностей при разных зёрнах. У WangHash статистические показатели образуют заметный паттерн. Но любую функцию можно прогнать через себя два раза и получить улучшенные показатели, как это показано в правом крайнем столбце WangDoubleHash. 

Также сегодня активно развивается и набирает популярность алгоритм xxHash.

Забегая вперёд, скажу, что мы выбрали этот генератор для наших проектов и активно его используем. 

Длительность последовательного генерирования у всех хеш-функций примерно одинакова. Однако у MD5 эта характеристика заметно отличается, но не потому, что алгоритм плохой, а потому что в стандартной реализации MD5 много разных состояний, которые влияют на быстродействие алгоритма. 

Оптимизация хеш-функций

Этот инструмент создавался для других целей — свёртки целых сообщений, поэтому на вход они принимают массивы данных. Лучше оптимизировать хеш-функции для задач генерирования случайных чисел, ведь нам достаточно подать два простых числа — зерно и счётчик. 

Что нужно сделать для оптимизации:

1. Убрать функцию включения хвоста. Это операция вставки недостающих элементов в конец массива для хеш-функции. Если его длина меньше требуемой для хеширования, недостающие элементы заполняются определёнными значениями, обычно нулями. 

2. Перевести обработку данных с типа byte на тип int.

3. Избавиться от конвертирования массива byte в одно число int.

Мы можем взять такую реализацию алгоритма xxHash:

uint h32;
var index = 0;
var len = buf.Length;

if (len >= 16)
{ 
	var limit = len - 16; 
	var v1 = seed + P1 + P2; 
	var v2 = seed + P2; 
	var v3 = seed + 0; 
	var v4 = seed - P1; 

	do 
	{  
		v1 = SubHash(v1, buf, index);  
		index += 4;  
		v2 = SubHash(v2, buf, index);  
		index += 4;  
		v3 = SubHash(v3, buf, index);  
		index += 4;  
		v4 = SubHash(v4, buf, index);  index += 4; 
	} while (index <= limit); 

	h32 = Rot32(v1, 1) + Rot32(v2, 7) + Rot32(v3, 12) + Rot32(v4, 18);
}
else
{ 
	h32 = seed + P5;
}
h32 += (uint) len;

while (index <= len — 4)
{ 
	h32 += BitConverter.ToUInt32(buf, index) * P3; 
	h32 = Rot32(h32, 17) * P4; 
	index += 4;
}

while (index < len)
{ 
	h32 += buf[index] * P5; 
	h32 = Rot32(h32, 11) * P1; 
	index++;
}
h32 ^= h32 >> 15;
h32 *= P2;
h32 ^= h32 >> 13;
h32 *= P3;
h32 ^= h32 >> 16;

return h32;

И уменьшить до такой:

public static uint GetHash(int buf, uint seed)
{ 
	var h32 = seed + P5; 
	h32 += 4U; 
	h32 += (uint) buf * P3; 
	h32 = Rot32(h32, 17) * P4; 
	h32 ^= h32 >> 15; 
	h32 *= P2; 
	h32 ^= h32 >> 13; 
	h32 *= P3; 
	h32 ^= h32 >> 16; 
	return h32;
}

Здесь Р1, Р2, Р3, Р4, Р5 — стандартные коэффициенты алгоритма xxHash. 

Комбинированные подходы

Комбинированные подходы бывают двух типов:

1. Сочетание хеш-функции и генератора случайных чисел. 

2. Иерархические генераторы. 

С первым всё предельно просто: берём хеш-функцию и получаем с её помощью зёрна, которые отправляем в другие генераторы. Слева показан результат работы комбинации стандартного Random из библиотеки C#, зёрна которому мы создавали с помощью хеш-функций. 

Второй подход гораздо интереснее. Мы его используем в ситуациях, когда нам необходимо генерировать группы последовательностей, например, ботов для тестирования. 

Сначала генерируем зёрна, а затем отправляем их в генераторы ботов. Первое число, полученное из генератора, мы используем как индекс для массива из ников игроков. Второе число будет зерном для генерирования истории матчей. Третье у нас используется для генерирования истории турнира. И т.п.

В этой иерархии могут применяться разные генераторы. Например, когда нам необходимо создать какую-то короткую последовательность, мы использовали перемешанный конгруэнтный генератор. А когда нам нужно было создать длинную историю матча, то использовали генератор Unity.

Мы разобрали наиболее популярные алгоритмы генераторов псевдослучайных чисел, рассмотрели альтернативу в виде хеш-функций, узнали, как их оптимизировать и прошлись по комбинированным подходам к генерированию псевдослучайных чисел. Надеюсь, что вам это было полезно!