Подобный Python Triton уже работает в ядрах, которые в 2 раза эффективнее эквивалентных реализаций Torch. А ядра матричного умножения FP16, сравнимые производительностью с cuBLAS, на Triton займут менее 25 строк. Как утверждает автор, многие программисты не могут написать такие ядра. Подробностями о Triton делимся к старту курса по ML и DL.

Новые исследовательские идеи в области Deep Learning обычно реализуются с помощью комбинации операторов нативного фреймворка. Это удобно, но часто требует создания (и/или перемещения) множества временных тензоров, что может снизить производительность нейросетей в большом масштабе. Проблемы решаются специализированными ядрами для GPU, но написать их может быть удивительно сложно из-за тонкостей программирования на GPU ^{1, 2, 3}.

И, хотя в последнее время появилось множество облегчающих труд систем^{4, 5}, мы обнаружили, что они либо слишком многословны, либо недостаточно гибкие, либо генерируют код заметно медленнее, чем настроенный вручную базовый. Это привело к расширению и улучшению Triton⁶, — нового языка и компилятора, создатель которого сейчас работает в OpenAI.

Проблемы программирования GPU

Архитектура современных GPU условно делится на три основных компонента — DRAM, SRAM и ALU. Оптимизируя код на CUDA, нужно учитывать каждый.

• Передачи памяти из DRAM должны быть объединены в большие транзакции, чтобы использовать большую ширину шины современных интерфейсов памяти.

• Данные должны быть вручную сохранены в SRAM перед повторным использованием и управляться таким образом, чтобы минимизировать конфликты между банками общей памяти при извлечении.

• Вычисления должны быть разделены и тщательно спланированы как между потоковыми мультипроцессорами (SM), так и внутри них, чтобы способствовать параллелизму на уровне инструкций/потоков и использовать специализированные ALU (например, тензорные ядра).

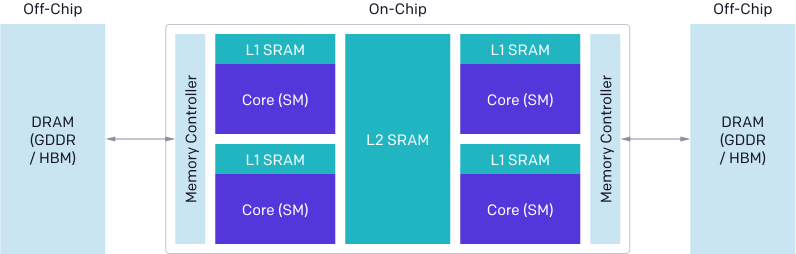
Учитывать эти факторы может быть сложно даже опытным программистам CUDA. Цель Triton — полностью автоматизировать эти оптимизации, чтобы разработчики сосредоточились на высокоуровневой логике параллельного кода. 

Triton стремится к широкому применению, и поэтому не составляет автоматического расписания работы между SM, оставляя некоторые важные алгоритмические соображения (например, тайлинг, синхронизация между SM) на усмотрение разработчиков.

Оптимизация компилятора в CUDA по сравнению с Triton.

Модель программирования

Из всех доступных доменно-специфических языков и JIT-компиляторов Triton, пожалуй, наиболее похож на Numba: ядра определяются как оформленные функции Python и запускаются параллельно с разными program_id на сетке так называемых instances (инстансов, экземпляров). 

Однако, как показано в приведённом ниже фрагменте кода, на этом сходство заканчивается: Triton раскрывает внутриэкземплярный параллелизм через операции над блоками — небольшими массивами, размеры которых равны степени двойки, — вместо модели выполнения Single Instruction, Multiple Thread (SIMT, одна инструкция — много потоков)⁷. 

При этом Triton эффективно абстрагируется от всех проблем, связанных с параллелизмом внутри блоков потоков CUDA (например, объединение памяти, синхронизация/конфликты общей памяти, планирование работы тензорных ядер).

Добавление вектора:

BLOCK = 512

# This is a GPU kernel in Numba.
# Different instances of this
# function may run in parallel.
@jit
def add(X, Y, Z, N):
   # In Numba/CUDA, each kernel 
   # instance itself uses an SIMT execution
   # model, where instructions are executed in
   # parallel for different values of threadIdx
   tid = threadIdx.x
   bid = blockIdx.x
   # scalar index
   idx = bid * BLOCK + tid
   if id < N:
     # There is no pointer in Numba.
     # Z,X,Y are dense tensors
     Z[idx] = X[idx] + Y[idx]


...
grid = (ceil_div(N, BLOCK),)
block = (BLOCK,)
add[grid, block](x, y, z, x.shape[0])

BLOCK = 512

# This is a GPU kernel in Triton.
# Different instances of this
# function may run in parallel.
@jit
def add(X, Y, Z, N):
   # In Triton, each kernel instance
   # executes block operations on a
   # single thread: there is no construct
   # analogous to threadIdx
   pid = program_id(0)
   # block of indices
   idx = pid * BLOCK + arange(BLOCK)
   mask = idx < N
   # Triton uses pointer arithmetics  
   # rather than indexing operators
   x = load(X + idx, mask=mask)
   y = load(Y + idx, mask=mask)
   store(Z + idx, x + y, mask=mask)


...
grid = (ceil_div(N, BLOCK),)
# no thread-block
add[grid](x, y, z, x.shape[0])

Хотя это может быть не особенно полезно для поэлементных вычислений, подход может значительно упростить разработку более сложных программ на GPU. Рассмотрим, например, случай ядра fused softmax, где каждый экземпляр нормирует отдельную строку заданного входного тензора X∈R^M×N. 

Стандартные CUDA-реализации этой стратегии распараллеливания могут быть сложными в написании, требуя явной синхронизации между потоками, поскольку они одновременно уменьшают одну и ту же строку XX. Большая часть этой сложности исчезает в Triton, где каждый экземпляр ядра загружает интересующую строку и последовательно нормализует её, используя NumPy-подобные примитивы.

Fused softmax в Triton:

import triton
import triton.language as tl

@triton.jit
def softmax(Y, stride_ym, stride_yn, X, stride_xm, stride_xn, M, N):
    # row index
    m = tl.program_id(0)
    # col indices
    # this specific kernel only works for matrices that 
    # have less than BLOCK_SIZE columns
    BLOCK_SIZE = 1024
    n = tl.arange(0, BLOCK_SIZE)
    # the memory address of all the elements
    # that we want to load can be computed as follows
    X = X + m * stride_xm + n * stride_xn
    # load input data; pad out-of-bounds elements with 0 
    x = tl.load(X, mask=n < N, other=-float('inf'))
    # compute numerically-stable softmax
    z = x - tl.max(x, axis=0)
    num = tl.exp(z)
    denom = tl.sum(num, axis=0)
    y = num / denom
    # write back to Y
    Y = Y + m * stride_ym + n * stride_yn
    tl.store(Y, y, mask=n < N)

import torch
# Allocate input/output tensors
X = torch.normal(0, 1, size=(583, 931), device='cuda')
Y = torch.empty_like(X)
# SPMD launch grid
grid = (X.shape[0], )
# enqueue GPU kernel
softmax[grid](Y, Y.stride(0), Y.stride(1), 
              X, X.stride(0), X.stride(1),
              X.shape[0]    , X.shape[1])

Обратите внимание, что Triton JIT рассматривает X и Y как указатели, а не тензоры; мы чувствовали, что сохранение низкоуровневого контроля доступа к памяти важно в обращении с более сложными структурами данных (например, блочно-рассеянных (block-sparse) тензоров). Важно отметить, что эта конкретная реализация softmax сохраняет строки XX в SRAM на протяжении всего процесса нормализации, что позволяет максимально переиспользовать данные, когда это возможно (~<32K столбцов). 

Иначе дело обстоит во внутреннем коде CUDA PyTorch, чьё использование временной памяти делает его более общим, но значительно более медленным (см. ниже). 

Triton упрощает разработку специализированных ядер, которые могут быть намного быстрее ядер в библиотеках общего назначения.

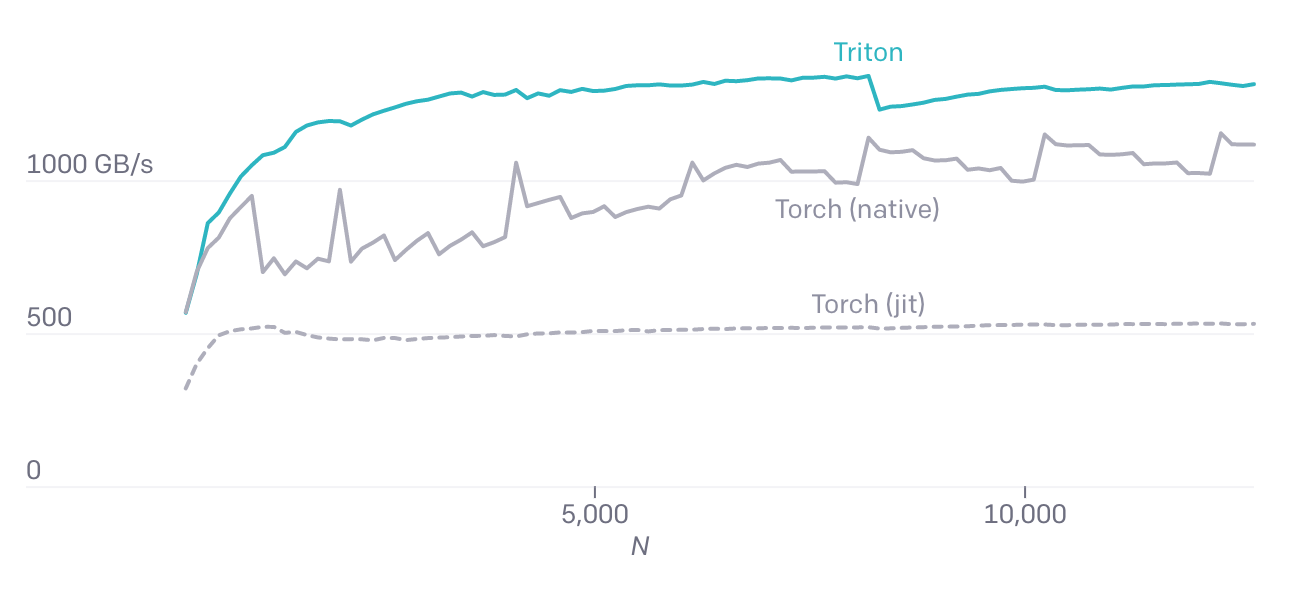
Более низкая производительность Torch (v1.9) JIT подчёркивает сложность автоматической генерации кода CUDA из последовательностей высокоуровневых тензорных операций. Fused softmax на Torch JIT:

@torch.jit.script
def softmax(x):
    x_max = x.max(dim=1)[0]
    z = x - x_max[:, None]
    numerator = torch.exp(x)
    denominator = numerator.sum(dim=1)
    return numerator / denominator[:, None]

Матричное умножение

Возможность писать "слитые" (fused) ядра (ядра с обобщением этапов вычислений) для операций и сокращений по элементам важна, но недостаточна, учитывая, что в нейронных сетях задачи умножения матриц занимают важное место. Как оказалось, Triton отлично подходит и для них, достигая пиковой производительности менее чем в 25 строк Python. С другой стороны, реализация чего-то подобного в CUDA потребует гораздо больше усилий и даже, скорее всего, приведёт к снижению производительности.

Умножение матриц при помощи Triton:

@triton.jit
def matmul(A, B, C, M, N, K, stride_am, stride_ak, 
            stride_bk, stride_bn, stride_cm, stride_cn,
            **META):
    # extract metaparameters
    BLOCK_M, GROUP_M = META['BLOCK_M'], META['GROUP_M']
    BLOCK_N = META['BLOCK_N']
    BLOCK_K = META['BLOCK_K']
    # programs are grouped together to improve L2 hit rate
    _pid_m = tl.program_id(0)
    _pid_n = tl.program_id(1)
    pid_m = _pid_m // GROUP_M
    pid_n = (_pid_n * GROUP_M) + (_pid_m % GROUP_M)
    # rm (resp. rn) denotes a range of indices
    # for rows (resp. col) of C
    rm = pid_m * BLOCK_M + tl.arange(0, BLOCK_M)
    rn = pid_n * BLOCK_N + tl.arange(0, BLOCK_N)
    # rk denotes a range of indices for columns 
    # (resp. rows) of A (resp. B)
    rk = tl.arange(0, BLOCK_K)
    # the memory addresses of elements in the first block of
    # A and B can be computed using numpy-style broadcasting
    A = A + (rm[:, None] * stride_am + rk[None, :] * stride_ak)
    B = B + (rk [:, None] * stride_bk  + rn[None, :] * stride_bn)
    # initialize and iteratively update accumulator
    acc = tl.zeros((BLOCK_M, BLOCK_N), dtype=tl.float32)
    for k in range(K, 0, -BLOCK_K):
        a = tl.load(A)
        b = tl.load(B)
        # block level matrix multiplication
        acc += tl.dot(a, b)
        # increment pointers so that the next blocks of A and B
        # are loaded during the next iteration
        A += BLOCK_K * stride_ak
        B += BLOCK_K * stride_bk
    # fuse leaky ReLU if desired
    # acc = tl.where(acc >= 0, acc, alpha * acc)
    # write back result
    C = C + (rm[:, None] * stride_cm + rn[None, :] * stride_cn)
    mask = (rm[:, None] < M) & (rn[None, :] < N)
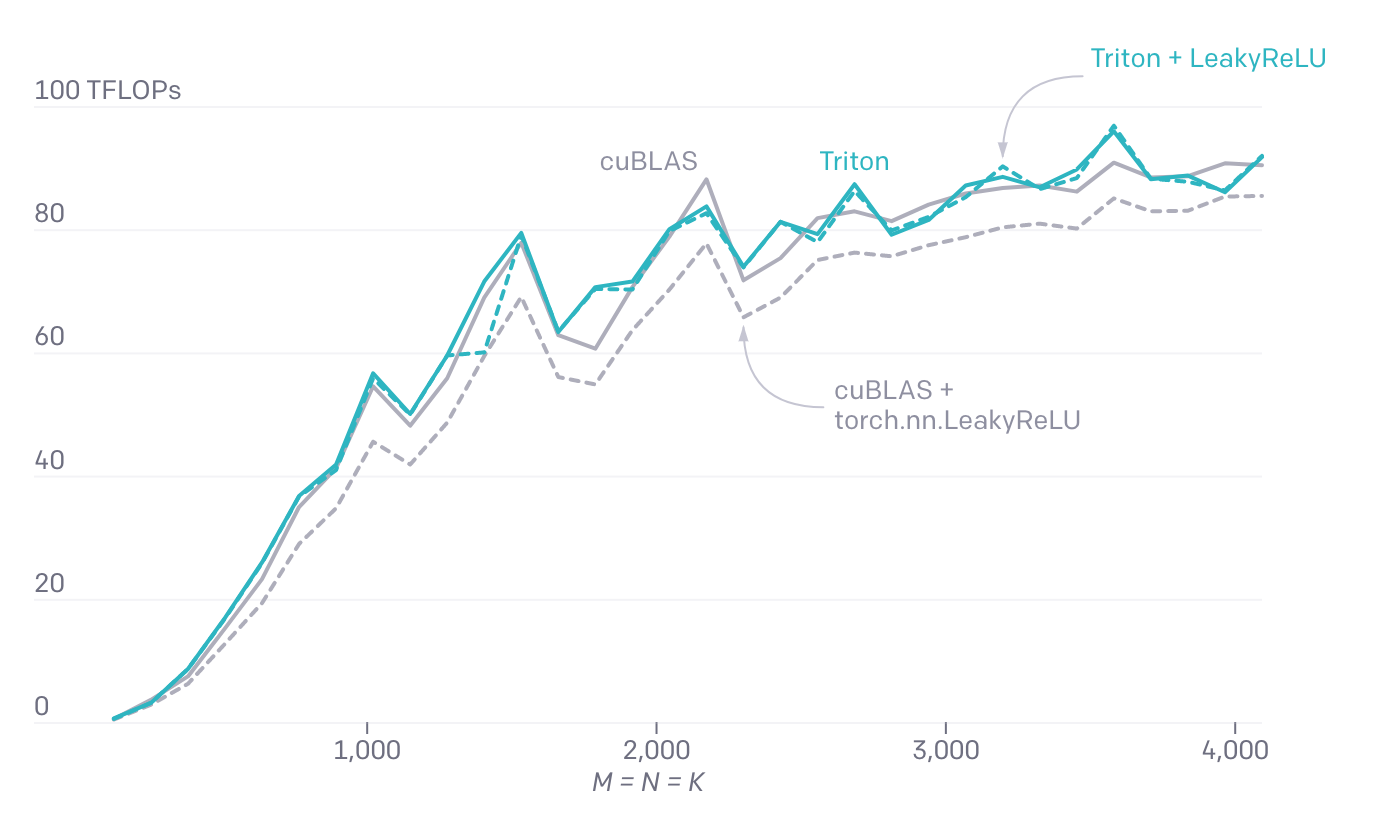
    tl.store(C, acc, mask=mask)

Одним из важных преимуществ рукописных ядер матричного умножения является то, что они могут быть настроены по желанию, чтобы разместить слитые преобразования их входных данных (например, слайсинга) и выходных (например, Leaky ReLU). Без Triton нетривиальные модификации ядер матричного умножения недоступны разработчикам без исключительного опыта программирования GPU.

Обзор архитектуры

Хорошая производительность Triton обусловлена модульной архитектурой системы, в центре которой — Triton-IR, то есть промежуточное представление на основе LLVM, где многомерные блоки значений — это самое важное.

@jit
def add(X, Y, Z, N):
   pid = program_id(0)
   idx= pid * 512 + arange(512)
   mask = idx < N
   x = load(X + idx, mask=mask)
   y = load(Y + idx, mask=mask)
   store(Z + idx, x + y, mask=mask)

def void add(i32* X .aligned(16) , i32* Y .aligned(16) , i32* Z .aligned(16) , i32 N .multipleof(2) )
{
entry:
  %0 = get_program_id[0] i32;
  %1 = mul i32 %0, 512;
  %3 = make_range[0 : 512] i32<512>;
  %4 = splat i32<512> %1;
  %6 = add i32<512> %4, %3;
  %9 = splat i32<512> N;
  %11 = icmp_slt i1<512> %6, %9;
  %14 = splat i32*<512> X;
  %16 = getelementptr i32*<512> %14, %6;
  %19 = broadcast i1<512> %11;
  %21 = splat i32<512> undef;
  %22 = masked_load i32<512> %16, %19, %21;
  %26 = splat i32*<512> Y;
  %28 = getelementptr i32*<512> %26, %6;
  %31 = broadcast i1<512> %11;
  %33 = splat i32<512> undef;
  %34 = masked_load i32<512> %28, %31, %33;
  %38 = splat i32*<512> Z;
  %40 = getelementptr i32*<512> %38, %6;
  %43 = add i32<512> %22, %34;
  %46 = broadcast i32<512> %43;
  %48 = broadcast i1<512> %11;
  masked_store void %40, %46, %48;
  ret void;
}

.visible .entry add(
    .param .u64 add_param_0, .param .u64 add_param_1,
    .param .u64 add_param_2, .param .u32 add_param_3
)
.maxntid 128, 1, 1
{
    .reg .pred     %p<4>;
    .reg .b32     %r<18>;
    .reg .b64     %rd<8>;
    ld.param.u64     %rd4, [add_param_0];
    ld.param.u64     %rd5, [add_param_1];
    mov.u32     %r13, %tid.x;
    ld.param.u32     %r14, [add_param_3];
    shl.b32     %r15, %r13, 2;
    mov.u32     %r16, %ctaid.x;
    mad.lo.s32     %r17, %r16, 512, %r15;
    setp.ge.s32     %p3, %r17, %r14;
    setp.lt.s32     %p1, %r17, %r14;
    mul.wide.s32     %rd7, %r17, 4;
    add.s64     %rd2, %rd4, %rd7;
    @%p1 ld.global.cg.v4.b32 {%r5,%r6,%r7,%r8}, [ %rd2 + 0];
    add.s64     %rd3, %rd5, %rd7;
    @%p1 ld.global.cg.v4.b32 {%r9,%r10,%r11,%r12}, [ %rd3 + 0];
    @%p3 bra     LBB0_2;
    ld.param.u64     %rd6, [add_param_2];
    add.s64     %rd1, %rd6, %rd7;
    add.s32     %r1, %r5, %r9;
    add.s32     %r2, %r6, %r10;
    add.s32     %r3, %r7, %r11;
    add.s32     %r4, %r8, %r12;
    st.global.v4.u32     [%rd1], {%r1, %r2, %r3, %r4};
LBB0_2:
    ret;
}

Декоратор @triton.jit работает, просматривая AST предоставленной функции Python, чтобы на лету сгенерировать Triton-IR, используя обычный алгоритм построения SSA⁸.

Полученный IR-код затем упрощается, оптимизируется и автоматически распараллеливается нашим бэкендом компилятора, после чего преобразуется в высококачественный LLVM-IR и, в конечном счёте, в PTX для выполнения на новейших графических процессорах NVIDIA. 

CPU и GPU AMD сейчас не поддерживаются, но мы приветствуем устраняющий это ограничение код.

Бэкенд компилятора

Мы обнаружили, что использование блочных представлений программ Triton-IR позволяет нашему компилятору автоматически выполнять широкий спектр важных оптимизаций. 

Данные могут автоматически укладываться в общую память, просматривая операнды вычислительно интенсивных операций на уровне блоков (например, tl.dot), и выделяться/синхронизироваться с помощью стандартных методов анализа живучести.

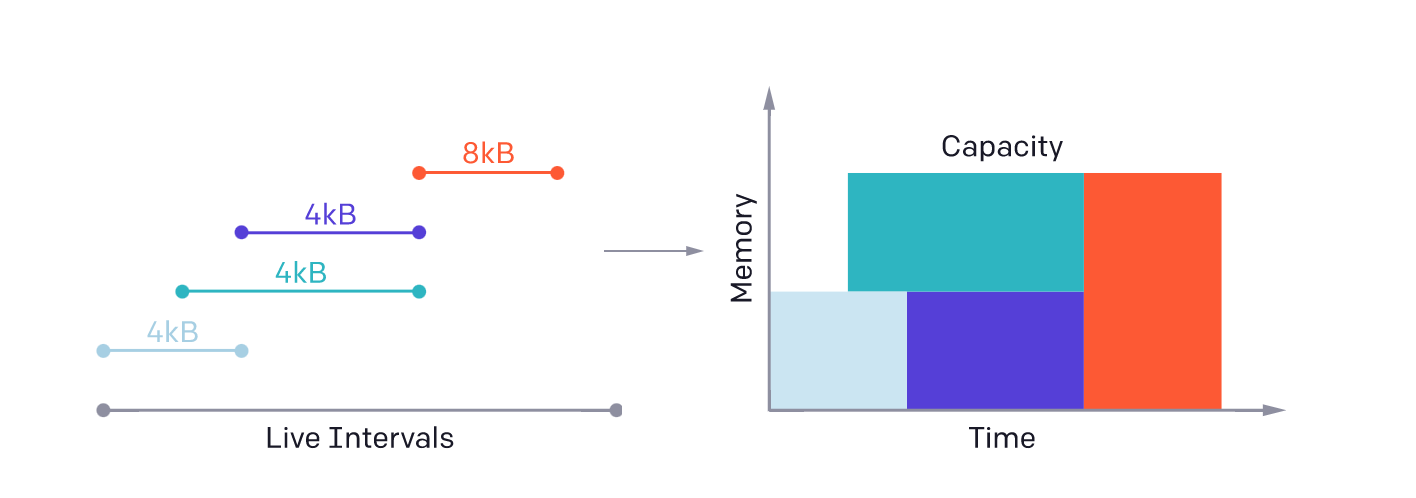
С другой стороны, программы Triton могут быть эффективно и автоматически распараллелены как (1) между SM — путём одновременного выполнения различных экземпляров ядра, так и (2) внутри SM — путём анализа пространства итераций каждой операции на уровне блоков и адекватного разбиения его на различные SIMD-блоки, как показано ниже.

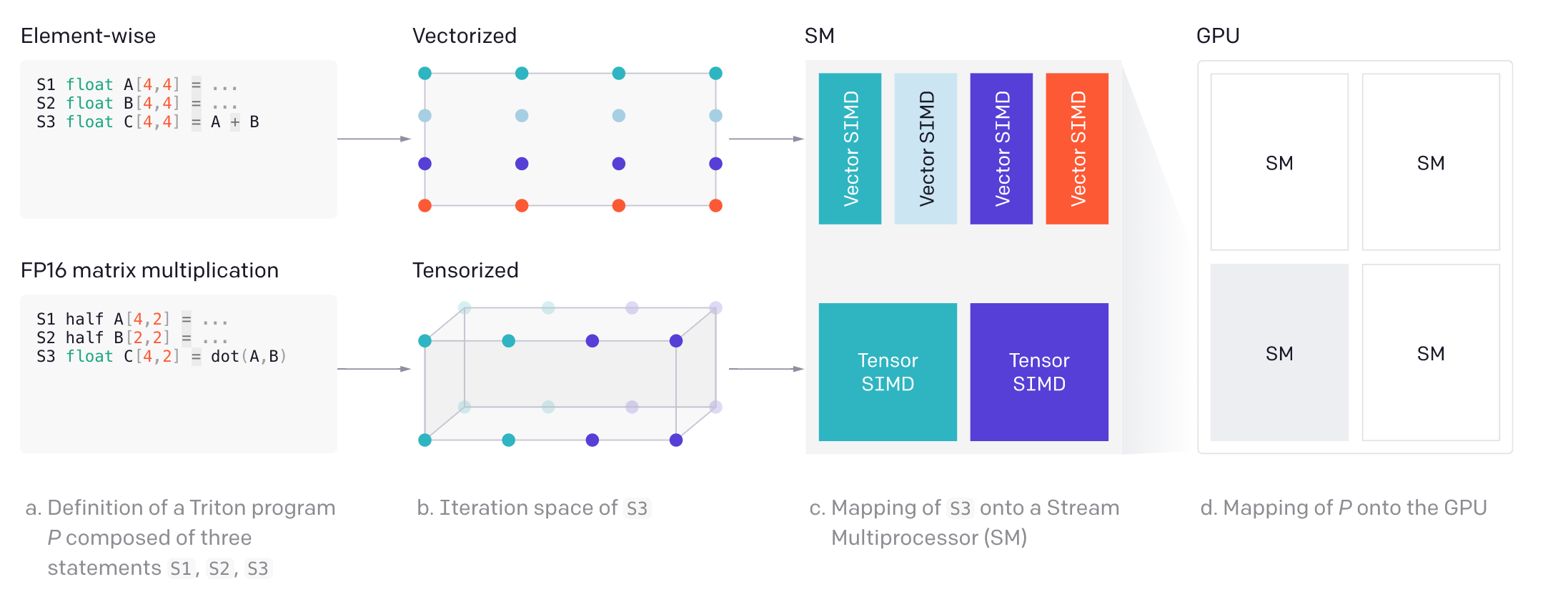
Код и крупные иллюстрации

S1 float A[4,4] = ...
S2 float B[4,4] = ...
S3 float C[4,4] = A + B

S1 half A[4,2] = ...
S2 half B[2,2] = ...
S3 float C[4,2] = dot(A,B)

Выше — определение программы Triton P, состоящей из трёх утверждений S1, S2, S3.

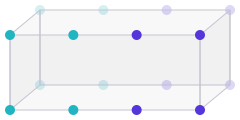
Пространство итерации S3.

Отображение S3 на потоковый мультипроцессор (SM).

Отображение P на GPU.

Заключение

В OpenAI намерены, чтобы проект Triton управлялся сообществом. Свободно форкайте репозиторий на GitHub. Документация Triton находится здесь. Попробовать Triton вы сможете на наших курсах:

• Курс по Machine Learning и Deep Learning (6 месяцев)

• Профессия Data Scientist (24 месяца)

А чтобы увидеть, как мы готовим специалистов в других направлениях IT, вы можете перейти на страницы из каталога.