Это вторая статья из цикла моих работ, посвящённых параллельным механизмам, а именно дельта-роботу. В прошлой статье ознакомились с конструкцией этого манипулятора, изучили историю по материалам других авторов и узнали о научных работах, которые велись и ведутся в рамках проектирования, усовершенствования и использования этого механизма. Сегодня начнём изучать дельта-робот более обстоятельно. Убедимся, что рабочий орган этого механизма имеет три степени свободы. Узнаем, что такое прямая и обратная задачи кинематики, решим их, решение проверим. Также расскажу, как я рисую "красивые" картинки и дам готовый код и 3Д модель для расчётов.

Нельзя не сказать о той статье, которая легла в основу моих рассуждений. На habr-е ещё в 2016-ом году была опубликована статья, посвящённая как раз решению обратной и прямой задач кинематики для дельта-робота. В ней, что называется, всё было расписано «для чайников» — просто и понятно. Читая её, я и пришёл к выводу, что все эти индексируемые в Scopus, Web of Science, РИНЦ журналы, увы, часто слабо помогают в освоении материала. Там люди пишут, по большей части, ради плюшек в виде прибавки к зарплате/стипендии а то и вообще, чтобы не уволили или ради того, чтобы похвалиться своим результатом, нормально не описав, как он получен. Журналы выставляют жёсткие требования на объём, содержание, оформление, что часто и приводит к тому, что полезную информацию приходится выцеживать из публикаций с огромным трудом. В общем, за основу я брал эту статью, и не в какое сравнение про доступности изложения она не идёт с теми, что я читал в рецензируемых журналах. Я во многом повторю материал из неё, даже картинки очень похожие будут (на них, кстати, убил кучу времени), но постараюсь дать больше информации, изложить её ещё более понятно и закинуть удочку в море дальнейшей работы.

В процессе повествования и под формулами и я буду расшифровывать все символы, входящие в уравнения и неравенства, но если вы уже вы в конце статьи и не знаете, что означает какой-то символ, а искать пояснение к нему не очень хочется, то поднимаемся сюда и открываем спойлер, в котором я привёл все обозначения, используемые в этой статье.

Я уже говорил, что дельта-робот имеет три поступательные степени свободы. Подтверждает ли это теория? Ответ под спойлером. Это мы нигде применять потом не будем, поэтому, если интересно, читаем, но потребуются некоторые знания теории механизмов и машин.

Определение числа степеней свободы дельта-робота по формуле Малышева

Для определения числа степеней свободы пространственного механизма используется формула Малышева ????:

где – число подвижных звеньев;

– число одноподвижных кинематических пар;

– число двухподвижных кинематических пар;

– число трёхподвижных кинематических пар;

– число четырёхподвижных кинематических пар;

– число пятиподвижных кинематических пар.

Звено механизма – это деталь или несколько неподвижно соединенных деталей, двигающихся как единое целое.

Кинематическая пара – это соединение двух соприкасающихся звеньев, допускающее их относительное движение.

Сначала, применим эту формулу к оригинальной конструкции, представленной на следующем рисунке:

Примечательно, что в ней используются только одноподвижные вращательные кинематические пары. Тогда для такого дельта-робота подвижность механизма получится Очевидно, что это не тот результат, которого мы ожидали. Как справедливо замечено в ???? при составлении уравнения Малышева никак не учтена особенность механизма, заключающаяся в том, что две штанги одного плеча являются сторонами параллелограмма, необходимого лишь для поддержания такой же ориентации подвижной платформы, как и у основания. Механизм будет работать идентично исходному, если мы уберём одну из штанг в каждом плече, но наложим условие, согласно которому ориентация каретки всегда будет такая же, как и у основания. В таком случае исходные данные будут иметь вид а подвижность механизма будет равна Что и есть в действительности.

Для анализа конструкции, показанной на рисунке ниже (с трёхподвижными шаровыми шарнирами), необходимо внести изменения в исходные данные для расчёта подвижности. После описанного выше упрощения при подвижность Тут стоит отметить появление шести местных подвижностей, а именно возможности вращения штанг вокруг своих осей, что на движение робота, в целом, никакого влияния не оказывает. Учитывая их, получим что также корректно.

Теперь перейдём к задачам кинематики. Ещё раз знакомая картинка, для понимания:

Определение углов поворота рычагов, при которых центр подвижной платформы будет иметь заданные координаты, называется обратной кинематической задачей. Решение этой задачи играет важнейшую роль, так как в большинстве случаев роботу будет подаваться команда о перемещении его рабочего органа в заданную точку, и система управления должна будет вычислить углы, на которые нужно повернуть валы каждого двигателя, чтобы выполнить эту команду. Установление связи между входными и выходными координатами называют также задачей о положениях.

Также существует и прямая кинематическая задача, в результате решения которой по известным углам поворота рычагов (их мы легко можем определить, если на осях вращения рычагов установлены датчики угла поворота) мы можем определить позицию, в которой сейчас находится рабочий орган. Это может понадобиться для различных расчётов, в рамках проектирования и управления роботом.

Обратная задача кинематики (ОЗК)

Для решения обратной кинематической задачи первоначально определим, какие конструктивные размеры нам известны. Известными будем считать длину стороны верхнего основания (треугольника, образуемого осями вращения рычагов), длину рычага (расстояние от оси рычага до общей оси трёхподвижных шарниров), длину штанги (расстояние между общими осями для трёхподвижных шарниров рычага и платформы) и длину стороны платформы (треугольника, образованного общими осями шарниров подвижной платформы). Кроме того, известными будем считать требуемые координаты центра платформы Определению подлежат углы поворота рычагов и отсчитываемые от плоскости основания (во многих источников отсчитывают от чего-то другого). Более наглядно эти параметры представлены на рисунке ниже

Сначала введём упрощение – заменим две штанги каждого плеча одной и допустим, что плоскости основания и платформы всё равно всегда будут параллельны. Введём систему координат, начало которой расположим в точке пересечения высот треугольника основания O. Ось Y направим вдоль одной из этих высот, ось X расположим перпендикулярно ей в плоскости основания, ось Z тогда окажется перпендикулярной плоскости основания. Выбор системы координат, а также все дальнейшие рассуждения, связанные с геометрией, иллюстрирует:

Постой, а как ты делаешь такие картинки?

Когда я задумал сделать первое такое изображение, я попытался найти, как похожие картинки делают другие люди. Ничего не найдя, я придумал свой способ.

Сначала в любой программе для 3Д моделирования (я использую Autodesk Inventor) делается "каркас" механизма:

Тут сразу я выбираю наиболее приятный глазу ракурс и делаю скриншонт области экрана.

Далее добавляю это изображение на отдельный слой в программе векторной графики Adobe Illustrator (можно использовать любою другую) и блокирую слой, чтобы случайно не сдвинуть его мышкой.

Далее кропотливо обвожу все фигуры и линии. Стараюсь грамотно распределить все примитивы по слоям, чтобы потом можно было легко их скрыть или изменить:

Другими способами я не пользовался. Если вы знаете способ лучше – пишите в комментарии.

Начнём с рассмотрения плеча, лежащего в плоскости YOZ. Для определения требуемого угла достаточно знать координаты точек Q и L, а вычислить угол можно по формуле:

где – координата точки L по оси Z;

– координата точки Q по оси y;

и т. д. по той же логике здесь и далее я буду обозначать координаты точек.

Координату точки Q по оси Y найдём с помощью известной для равностороннего треугольника формулы поиска радиуса вписанной окружности:

где – длина стороны треугольника основания.

Пару слов о F и f

По существу,– это радиус вписанной в треугольник основания окружности OQ:

Часто дельта-робот и рисуют не с треугольником в основании, а с окружностью. В подавляющей части расчётов длина стороны нигде не используется, а используется именно OQ. А вот и пример.

Для того, чтобы найти координаты точки L проанализируем траектории движения концов рычага и штанги. Точка L, принадлежащая рычагу, описывает окружность в плоскости YOZ с центром в точке Q. Точка M является трёхподвижной парой, поэтому точка L, принадлежащая штанге описывает сферу с центром в точке M. Следовательно, для определения координаты точки L всего механизма нужно найти точку пересечения сферы и окружности. Таких точек пересечения две – L и L₁, нам же нужно выбрать точку, у которой координата по оси Y меньше. Соответственно, мы должны решить систему из двух уравнений:

где – длина рычага;

– длина штанги.

Координату точки M по оси Y, найдём по формуле, аналогичной формуле (2):

где – длина стороны треугольника платформы.

Остальные координаты точки M будут равны соответствующим координатам точки V, что приведёт нас к итоговой системе:

Раскрыв скобки в первом и втором уравнениях и вычтя из первого уравнения второе, получим равенство, из которого линейным образом можно выразить по формуле:

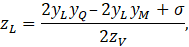
где

Тогда, подставив это в первое уравнение системы и приведя его к виду квадратного уравнения относительно можно составить систему для расчёта коэффициентов квадратного уравнения:

Далее найдём меньший корень квадратного уравнения по формуле ниже и подставим полученное решение в формулу (6), найдя тем самым неизвестную координату точки L по оси Z.

Можно, конечно, подставить все расчёты в исходную формулу (1), но получится громоздко и не наглядно. Выполняя это простую последовательность отдельных вычислений мы всё равно придём к нужному результату.

Заметим, что найти угол поворота первого плеча можно и другим способом. Мы можем перейти к плоской задаче, так как знаем, что плоскость YOZ пересекает сферическую траекторию конца штанги по окружности с центом в точке N, что показано на рисунке:

Радиус этой окружности – NL можно найти из прямоугольного треугольника LMN по теореме Пифагора. Так как сторона NM, по факту, является координатой точки V по оси X, а сторона LM штангой длины то получим формулу:

Перейдём в плоскость YOZ и рассмотрим треугольник QLN. Сторону NQ мы можем найти, зная координаты точек N и Q по формуле:

Длины остальных сторон нам тоже известны, следовательно, по теореме косинусов мы можем найти угол :

Необходимый нам угол найдём как арккосинус по формуле:

Тогда искомый угол найдём, как разность полного оборота и найденных углов:

Для поиска двух оставшихся углов поворота рычагов воспользуемся следующим приёмом. Введём вспомогательную систему координат, повёрнутую на 120° вокруг оси Z относительно основной :

В новой системе координат задача для определения угла сводится к задаче определения угла с той лишь разницей, что координаты точки V нужно перевести из XYZ в по известным формулам:

где – координаты точки V по осям X и Y в системе координат

Аналогичным образом можно рассчитать угол поворота третьего рычага, введя систему координат, повёрнутую на 240°.  Заметим, что данные формулы справедливы лишь для случая, когда мы находим координаты точки в системе, повёрнутой по часовой стрелке относительно основной.

В совокупности полученный результат называют также функцией положения.

Прямая задача кинематики (ПЗК)

Исходными данными для решения прямой кинематической задачи являются углы поворота рычагов. Зная эти углы, мы можем из прямоугольного треугольника Q₁W₁L₁, расположенного в плоскости YOZ (рисунок ниже) найти координаты точки L₁.

Используя найденную ранее координату точки Q, получим формулы:

Для поиска координат по оси Z оставшихся точек L₂ и L₃ применим аналогичные формулы:

С другой стороны, для поиска координат по оси Y воспользуемся уже известным приёмом – вычислим координаты по этой оси в системах координат, повёрнутых на 120° и 240° относительно основной, обозначив их а потом пересчитаем их в основную систему координат по формулам ниже. В отличие от зависимостей (14), применим формулы для пересчёта в систему, повёрнутую против часовой стрелки относительно основной.

Нам известно, что точки L₁, L₂ и L₃ представляют собой трёхподвижные шарниры, и, если принять эти точки за центры вращения, то их концы – точки M₁, M₂ и M₃ описывают 3 сферы. Далее сдвинем каждую штангу параллельно плоскости XOY так, чтобы точки M₁, M₂ и M₃ оказались в точке V, что наглядно показано на рисунке:

Теперь рассматриваемые сферы (уже с центрами в точках P₁, P₂ и P₃) пересекаются как раз в точке V. Для поиска координат новых центров сфер перейдём в плоскость XOY (рисунок ниже). Для поиска координаты точки P₁ достаточно сдвинуть координату по оси Y точки L₁ на в большую сторону.

Координаты остальных точек легко найти, рассматривая прямоугольный треугольник VM₃T, гипотенуза которого равна так же . Из него координаты точек P₂ и P₃ определим по формулам:

После вышеизложенных расчётов мы можем найти необходимые координаты точки V, как меньшее по оси Z решение системы уравнений (19), представляющее собой нижнюю точку пересечения трёх сфер.

Чтобы получить решение, первым шагом, раскроем скобки и перенесём все известные слагаемые вправо:

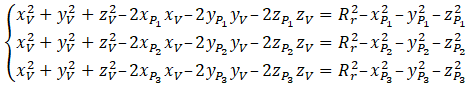
Правые части уравнений в системе сразу обозначим за константы а затем вычтем из первого уравнение второе, а потом из первого третье, тем самым получив систему:

В этой системе вынесем за скобки и поделим левую и правые части на 2. Получим систему:

Обозначим за соответственно. Во втором уравнении введём аналогичные обозначения, но с индексами равными 2. Выразим из получившейся системы через получив уравнения:

Тогда, подставив это в первое уравнение системы (19), получим квадратное уравнение (24) относительно переменной вычислив меньший корень которого, найдём интересующую нас координату точки V по оси Z.

где

Зная координату найдём оставшиеся координаты точки V по уже найденным формулам (23).

Алгоритмы расчёта и их проверка

Мы нашли решения ОЗК и ПЗК. Хорошо. Теперь, чтобы без опаски использовать полученные формулы в алгоритмах расчёта, наши решения нужно проверить.

Способов проверки можно выделить несколько:

• можно решить ОЗК двумя приведёнными способами для одних и тех же конфигурации механизма и заданного положения, и посмотреть, совпадают ли результаты;

• можно решить ОЗК, а потом, используя найденные углы, решить ПЗК (должно получиться исходное положение);

• можно построить дельта-робота с указанными размерами в какой-нибудь программе для трёхмерного моделирования и сравнить, какие углы соответствуют определённому положению в полученной 3Д модели, а какие получаются при расчётах по формулам.

Начнём с алгоритма для решения ОЗК. Я работаю пакете MATLAB, поэтому привожу код для этой среды расчётов и программирования. "Решатель" ОЗК состоит из трёх файлов. В первом (основном) задаются размеры робота и желаемые координаты точки центра платформы V:

%Объявляем глобальные переменные характерных размеров робота и констант
global R_l R_r  VM OQ cos120 sin120 cos240 sin240
%Вычисляем константы
cos120 = cosd(120);
sin120 = sind(120);
cos240 = cosd(240);
sin240 = sind(240);
%Задаём размеры робота [мм]
F = 270; %Длина стороны треугольника основания
f = 80; %Длина стороны треугольника платформы
R_l = 170;  %Длина рычагов (по осям)
R_r = 320;  %Длина штанг (по осям)
%Вычисляем радиусы вписанных окружностей
OQ = F*sqrt(3)/6; %Радиус окружности осей шарниров
VM = f*sqrt(3)/6; %Радиус окружности осей рычагов
%Задаём желаемые координаты центра подвижной платформы [мм]
X_V = 10; %Координата по оси X
Y_V = 30; %Координата по оси Y
Z_V = -310; %Координата по оси Z
%Вычисляем углы, на которые нужно повернуть рычаги
[Theta1, Theta2, Theta3] = OZK(X_V, Y_V, Z_V)

В конце приведённого кода вызывается функция, которая и решает ОЗК:

%Находит решение обратной задачи кинематически для дельта-робота
function [Theta1, Theta2, Theta3] = OZK(X_V, Y_V, Z_V)
%Расчёт координат точки V в системах координат, повёрнутых на 120° и 240°
%по часовой стрелке относительно основной
global cos120 sin120 cos240 sin240
X_V_120 = X_V*cos120 - Y_V*sin120;
Y_V_120 = X_V*sin120 + Y_V*cos120;
    X_V_240 = X_V*cos240 - Y_V*sin240;
    Y_V_240 = X_V*sin240 + Y_V*cos240;
%Расчёт углов поворота рычагов в соответствующих системах координат
Theta1 = Theta(X_V, Y_V, Z_V);
Theta2 = Theta(X_V_120, Y_V_120, Z_V);
Theta3 = Theta(X_V_240, Y_V_240, Z_V);
end

А в ней вызываются функции, которые считают углы для каждого рычага в отдельности:

%Находит углы поворота рычагов в соответствующих системах координат
function [Theta] = Theta(X_V, Y_V, Z_V)
global R_l R_r  VM OQ
y_M = -VM + Y_V;
y_Q = -OQ;
%Первый метод вычисления
sigma = R_l^2 - R_r^2 + X_V^2 + y_M^2 - y_Q^2 + Z_V^2;
a = (2*y_M - 2*y_Q)^2/(4*Z_V^2) + 1;
b = - 2*y_Q - ((2*y_M - 2*y_Q)*sigma)/(2*Z_V^2);
c = sigma^2/(4*Z_V^2) - R_l^2 + y_Q^2;
y_L = (-b-sqrt(b^2-4*a*c))/(2*a);
z_L = ( - 2*y_L*y_M  + 2*y_L*y_Q + sigma)/(2*Z_V);
Theta = 180 + atand((-z_L)./(y_Q-y_L));
%Второй метод вычисления
% NL = sqrt(R_r^2-X_V^2);
% const_1 = y_M - y_Q;
% NQ = sqrt(const_1^2 + Z_V^2);
% Theta = 360 - acosd((R_l^2 + NQ^2 - NL^2)/(2*R_l*NQ)) - acosd(const_1/NQ);
end

Можно заметить, что в последней функции можно использовать два разных метода, которые описаны выше. Решения при использовании и того, и другого совпадают.

Кстати, если задать в алгоритм такую точку, в которую конкретный дельта-робот не сможет поместить свой рабочий орган, то программа всё равно найдёт решение ОЗК, но последнее будет мнимым. Например, Theta1 = 99.4457 - 25.7939i, Theta2 = 95.4333 - 24.1706i, Theta3 = 93.4994 - 23.0821i.

Далее сделаем проверку, которая даст нам ещё +100% к гарантии того, что формулы правильные. В Autodesk Inventor (или любой другой среде, где можно создавать 3Д модели) можно создать модель дельта-робота, состоящую лишь из линий эскизов. С умом используя возможность параметризации, я получил такую модель:

В эту модель также, как и в программу, представленную выше, вводятся размеры робота и координаты центра платформы. В результате вычисления последних трёх параметров можно увидеть интересующие нас углы. Решение, полученное таким образом совпадает с решением, полученным алгоритмом в MATLAB.

Не буду вдаваться в подробности, как строить такие модели, если очень интересно, пишите в комментариях. Вот ссылка на мою модель в формате .ipt для Inventor-а 2022 и выше.

Кому-то данный способ проверки может показаться слишком топорным и глупым. Но именно его я использовал для исправления ошибок в формулах и в записи их в MATLAB.

ПЗК проверим по второму способу – найдём решение ОЗК для конкретных координат точки V по алгоритму выше (а он правильный).

А далее введём полученные данные в качестве входных значения алгоритма ПЗК. Последний состоит из двух файлов. Первый, как и для ОЗК, основной:

%Объявляем глобальные переменные характерных размеров робота и констант
global R_l R_r  VM OQ cos120 sin120 cos240 sin240
%Вычисляем константы
cos120 = cosd(120);
sin120 = sind(120);
cos240 = cosd(240);
sin240 = sind(240);
%Задаём размеры робота [мм]
F = 270; %Длина стороны треугольника основания
f = 80; %Длина стороны треугольника платформы
R_l = 170;  %Длина рычагов (по осям)
R_r = 320;  %Длина штанг (по осям)
%Вычисляем радиусы вписанных окружностей
OQ = F*sqrt(3)/6; %Радиус окружности осей шарниров
VM = f*sqrt(3)/6; %Радиус окружности осей рычагов
%Задаём желаемые координаты центра подвижной платформы [мм]
Theta1 = 211.1864; %Координата по оси X
Theta2 = 202.9511; %Координата по оси Y
Theta3 = 198.8468; %Координата по оси Z
%Вычисляем углы, на которые нужно повернуть рычаги
[L1, L2, L3, V] = PZK(Theta1, Theta2, Theta3)

А второй – это функция непосредственно для решения прямой задачи:

%Находит решение прямой задачи кинематически для дельта-робота
%Возвращает координаты точек L1, L2, L3, необходимые для построения робота и
%координаты точки V
function [L1, L2, L3, V] = PZK(Tetta1, Tetta2, Tetta3)
global R_l R_r VM OQ
%Расчёт координат концов рычагов
x_L1 = 0;
y_L1 = -OQ-R_l*cosd(Tetta1-180);
z_L1 = -R_l*sind(Tetta1-180);
z_L2 = -R_l*sind(Tetta2-180);
z_L3 = -R_l*sind(Tetta3-180);
y_L2S = -OQ-R_l*cosd(Tetta2-180);
y_L3S = -OQ-R_l*cosd(Tetta3-180);
x_L2 = y_L2S*sind(120);
y_L2 = y_L2S*cosd(120);
x_L3 = y_L3S*sind(240);
y_L3 = y_L3S*cosd(240);
%Расчёт координат центров сфер (сдвинутых концов рычагов)
x_P1 = x_L1;
y_P1 = y_L1+VM;
z_P1 = z_L1;
x_P2 = x_L2+VM*cosd(30);
y_P2 = y_L2-VM*sind(30);
z_P2 = z_L2;
x_P3 = x_L3-VM*cosd(30);
y_P3 = y_L3-VM*sind(30);
z_P3 = z_L3;
%Расчёт точки пересечения сфер
w1 = R_r^2-x_P1^2-y_P1^2-z_P1^2;
w2 = R_r^2-x_P2^2-y_P2^2-z_P2^2;
w3 = R_r^2-x_P3^2-y_P3^2-z_P3^2;
a1 = x_P2-x_P1;
a2 = x_P3-x_P1;
b1 = y_P2-y_P1;
b2 = y_P3-y_P1;
c1 = z_P2-z_P1;
c2 = z_P3-z_P1;
d1 = (w1-w2)/2;
d2 = (w1-w3)/2;
e1 = ((b1*c2 - b2*c1)/(a1*b2 - a2*b1));
f1 = -(b1*d2 - b2*d1)/(a1*b2 - a2*b1);
e2 = -(a1*c2 - a2*c1)/(a1*b2 - a2*b1);
f2 = (a1*d2 - a2*d1)/(a1*b2 - a2*b1);
a_KU = (e1^2 + e2^2 + 1);
b_KU = (2*e1*(f1 - x_P1) - 2*z_P1 + 2*e2*(f2 - y_P1));
c_KU = z_P1^2 + (f1 - x_P1)^2 + (f2 - y_P1)^2 - R_r^2;
z_V = ((-b_KU-sqrt(b_KU^2-4*a_KU*c_KU)))/(2*a_KU);
x_V = e1*z_V+f1;
y_V = e2*z_V+f2;
L1 = [x_L1, y_L1, z_L1];
L2 = [x_L2, y_L2, z_L2];
L3 = [x_L3, y_L3, z_L3];
V = [x_V, y_V, z_V];
end

Применяя эту программу, получим исходную точку, что говорит о корректности и этого алгоритма.

А, выдаёт он нам решения при любых значениях углов и ему абсолютно всё равно, что реальный дельта-робот в таком положении оказаться не может:

Алгоритм ещё и находит координаты точек концов рычагов L₁, L₂ и L₃. В дальнейшем это используется для построения робота в осях трёхмерного графика, но об этом в следующей статье.

Надеюсь рассказал обо всём понятно и наглядно. Вообще, всё, что я тут показывал, несёт большой смысл. Всё это будет использовано при написании прошивки, управляющей дельта-роботом, и при дальнейших расчётах направленных на конструирование конкретной его реализации "в железе".

На ответы в комментариях не всегда хватает времени, так что, если не ответил, – извиняйте. В следующей статье будем строить рабочую зону дельта-робота.