Еще раз здравствуй, Хабр! Меня зовут Мария Белялова, и я занимаюсь data science в мобильном фоторедакторе Prequel. Кстати, именно в нём и обработана фотография из шапки поста.

Эта вторая статья в нашем цикле материалов про сравнение алгоритмов оптимизации для обучения нейросетей. В первой части мы сравнивали поведение 39 алгоритмов на тестовых функциях. Если вы ее еще не читали, то советуем начать с нее. Также в прошлой статье мы кратко рассказали, в связи с чем появляется так много разных оптимизаторов для нейросетей.

В этой статье мы посмотрим, как они ведут себя на игрушечной задаче — распознавании цифр из датасета MNIST. В следующей части мы проверим эти алгоритмы в бою на реальной задаче из продакшена. Код для этой и предыдущей части находится здесь.

Условия эксперимента

В качестве игрушечной задачи мы выбрали классификацию черно-белых изображений с рукописными цифрами из датасета MNIST. Этот датасет в силу своей простоты является популярным выбором для тестирования алгоритмов. Он содержит 60 000 тренировочных изображений и 10 000 тестовых изображений, каждое из которых принадлежит одному из 10 классов, которые соответствуют числу на изображении.

В качестве классификатора мы взяли простую модель с двумя сверточными слоями, двумя полносвязными слоями, макспулингом и дропаутом:

class Net(nn.Module):
	def __init__(self, n_classes=10):
    	super(Net, self).__init__()
    	self.conv1 = nn.Conv2d(1, 32, 3, 1)
    	self.conv2 = nn.Conv2d(32, 64, 3, 1)
    	self.dropout1 = nn.Dropout(0.25)
    	self.dropout2 = nn.Dropout(0.5)
    	self.fc1 = nn.Linear(9216, 128)
    	self.fc2 = nn.Linear(128, n_classes)

	def forward(self, x):
    	x = self.conv1(x)
    	x = F.relu(x)
    	x = self.conv2(x)
    	x = F.relu(x)
    	x = F.max_pool2d(x, 2)
    	x = self.dropout1(x)
    	x = torch.flatten(x, 1)
    	x = self.fc1(x)
    	x = F.relu(x)
    	x = self.dropout2(x)
    	x = self.fc2(x)
    	output = F.log_softmax(x, dim=1)
    	return output

В качестве функции потерь использовался negative log likelihood loss. Во всех экспериментах модель инициализируется одинаковыми весами.

С каждым алгоритмом оптимизации модель обучалась:

• на сетке из 4 learning rate и 6 размерах батча — 48 раз;
• с 12 разными learning rate schedulers с двумя парами фиксированных learning rate и размером батча (ниже расскажем, как мы их выбрали) — 24 раза.

В экспериментах участвовали 36 алгоритмов оптимизации (в прошлой статье мы рассматривали 39 алгоритмов, в этой мы не рассматриваем LBFGS, Shampoo и Adafactor, так как они обучались слишком долго — при таком количестве экспериментов мы не могли себе это позволить). Всего модель была обучена 2592 раз с разными параметрами и оптимизаторами.

Сравнение с разными learning rate

Фиксируем размер батча на 64 и обучим модель со всеми оптимизаторами с разными learning rate: 1e-2, 1e-3, 1e-4 и 1e-5. В роли метрики качества выбрана accuracy, потому что в MNIST нет ярко выраженного дисбаланса классов.

Так выглядят графики accuracy от эпохи обучения, функции потерь на обучении (train loss) и на тесте (test loss) для learning rate = 1e-4 — с этим значением графики наиболее наглядны. В легенде на графике accuracy алгоритмы отсортированы по максимальной достигнутой accuracy, а также указан номер эпохи, на которой она достигается. В легенде на графиках train loss и test loss алгоритмы отсортированы по минимальному достигнутому ими значению функции потерь, и указано место алгоритма по accuracy (чем меньше номер, тем больше accuracy). На графиках train loss и test loss нет алгоритма Rprop из-за масштабирования (это единственный алгоритм, с которым loss возрастает), с ним график перестает быть наглядным. 



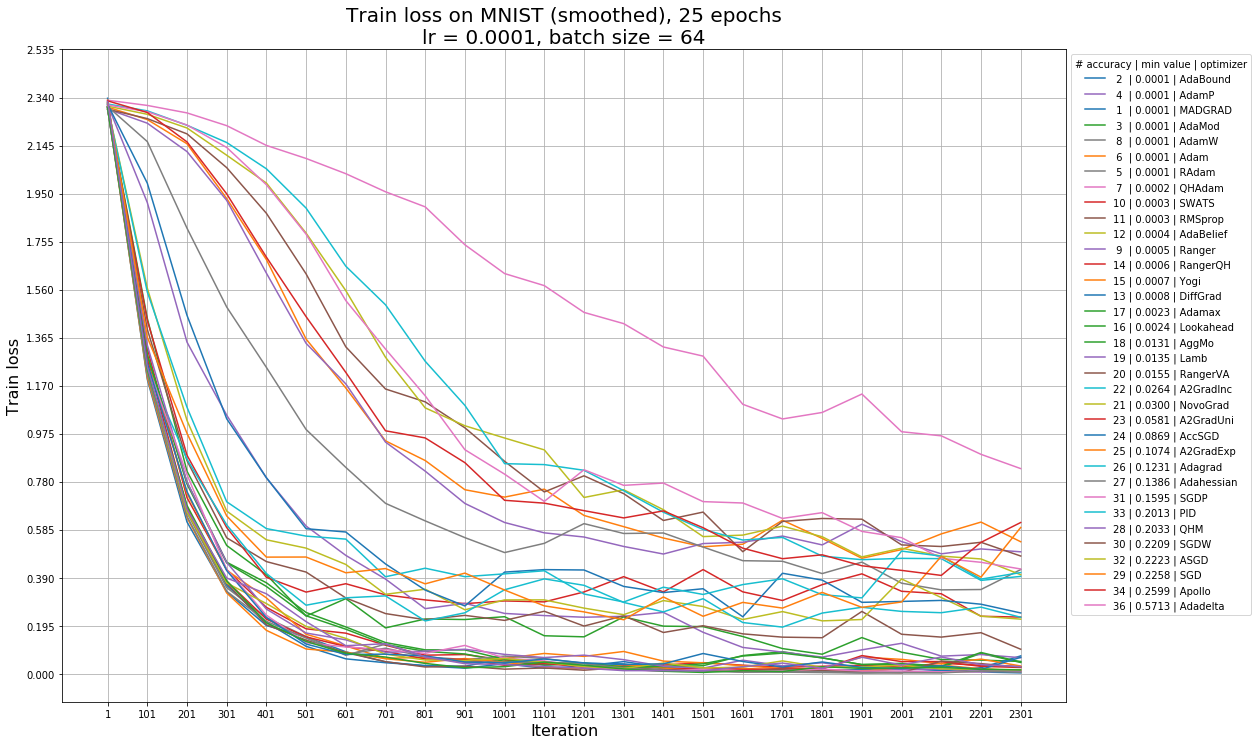
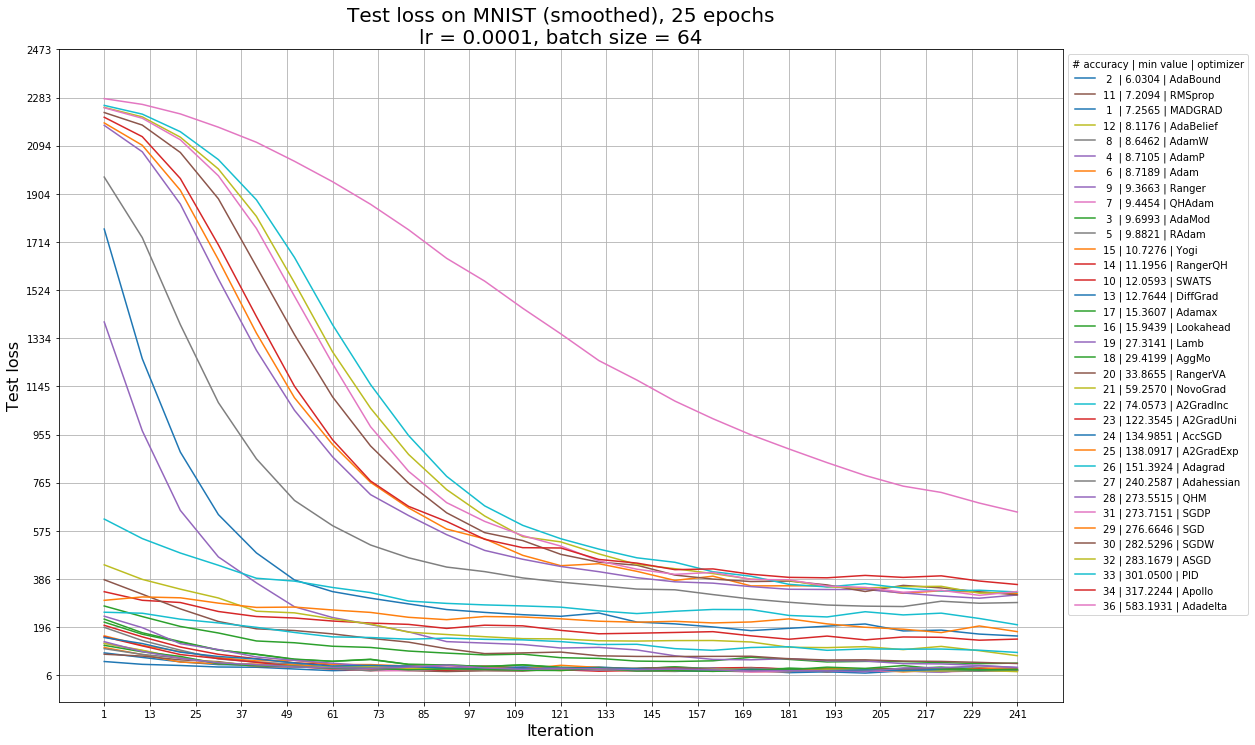
Для того, чтобы понять, какие алгоритмы наиболее устойчивы к изменению learning rate, отсортируем их по средней accuracy моделей, обученных с разными learning rate. В таблицах ниже также приведены среднеквадратическое отклонение, минимальное и максимальное значения, и learning rate, на котором было достигнуто максимальное значение accuracy. Чем больше значение в столбце, тем ближе оно к зеленому, чем меньше, тем ближе к красному. В таблице 1 представлены результаты того, как алгоритмы обучались в течение 25 эпох. Далее мы также приведем таблицу с результатами обучения на 50 эпохах для того, чтобы посмотреть, каким из алгоритмов требуется больше времени, чтобы сойтись, и какие алгоритмы при более длительном обучении не покажут особых улучшений.

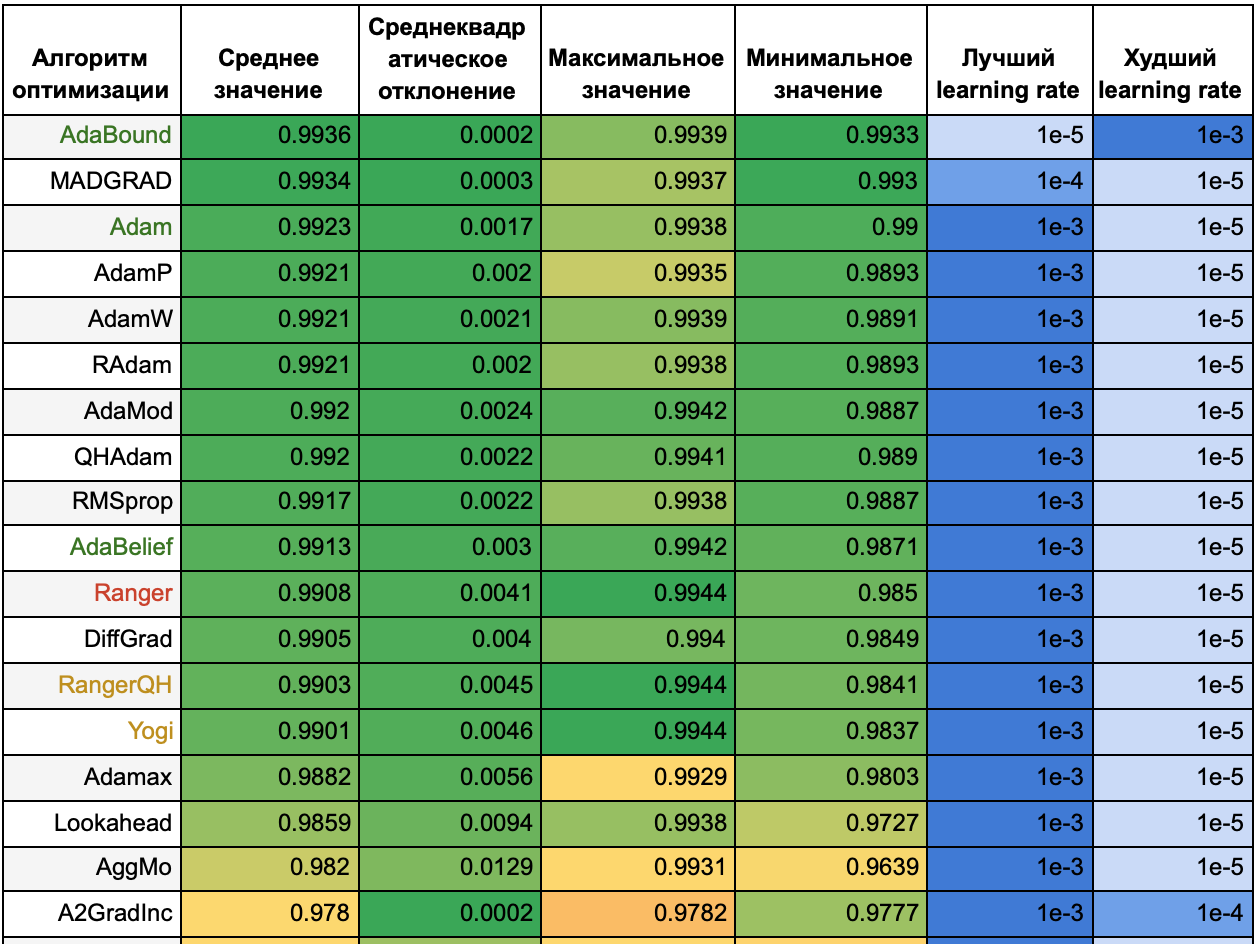
Таблица 1. 



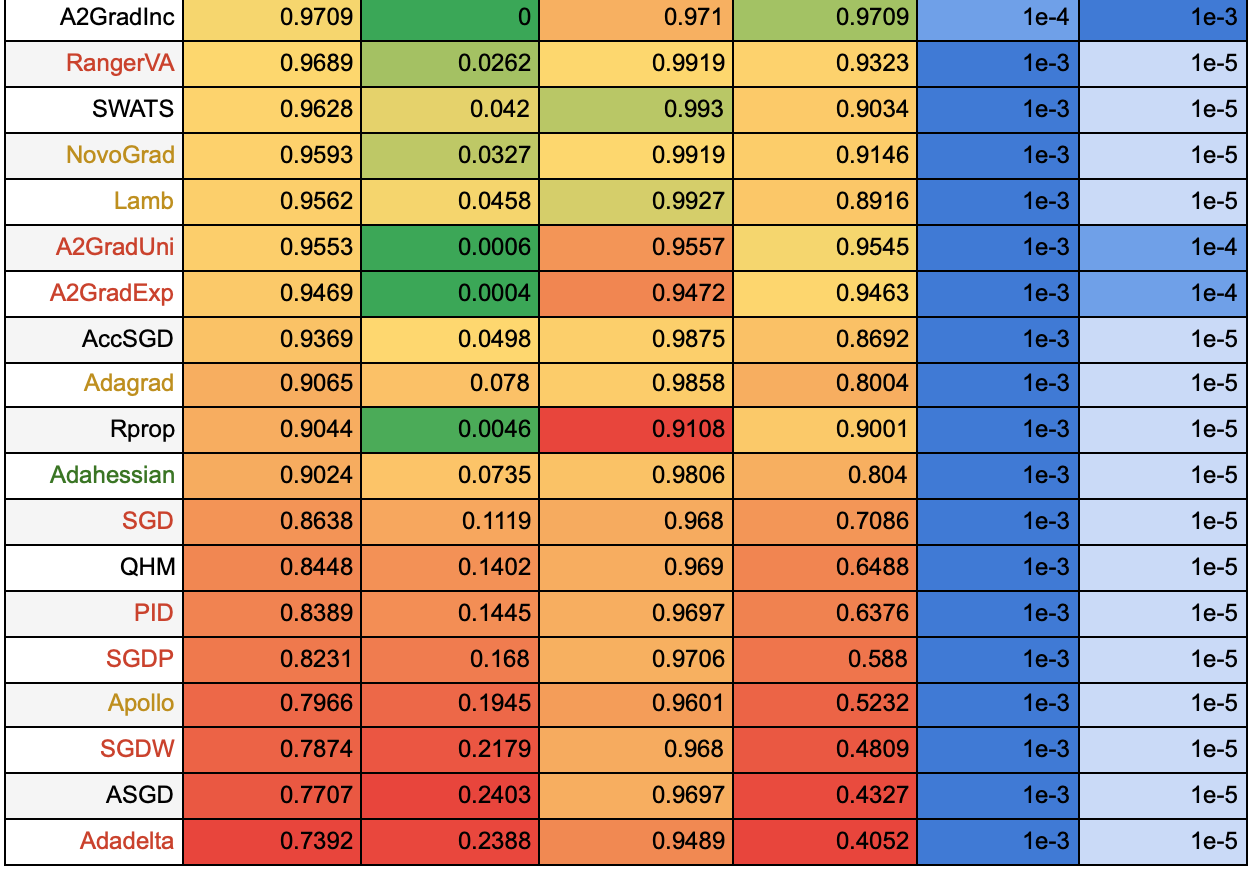
Названия алгоритмов выделены цветом по тому же принципу, что и в предыдущей статье: зеленым цветом отмечены те алгоритмы, которые хорошо себя показали на обеих тестовых функциях, желтым — средне, красным — плохо. На примере этой таблицы можно убедиться, что не стоит выбирать алгоритм по тестовым функциям: так, алгоритмы MADGRAD, AdaMod, Ranger, Yogi не оказались в числе лидеров ни для одной из тестовых функций, но на данной задаче показали хорошие результаты. Среди алгоритмов, которые оказались лучше всех на обеих тестовых функциях, на этой задаче тоже оказались в лидерах адаптивные алгоритмы первого порядка AdaBound, Adam, AdaBelief. Результаты алгоритма второго порядка Adahessian оказались ближе к худшим.

По таблице видно, что многие алгоритмы показывают худшие результаты на маленьком learning rate = 1e-5. Посмотрим на таблицу для 50 эпох, чтобы понять, какие алгоритмы продолжают медленно обучаться и дальше, а какие уже сошлись на 25 эпохах.

Таблица 2.



Для наглядности сопоставим результаты обучения в течение 25 эпох и 50 эпох. В следующей таблице приведено место алгоритма по accuracy на 25 на 50 эпохах, как это место изменилось (красным выделены алгоритмы, которые упали в рейтинге, зеленым — которые поднялись), и средние accuracy на 25 и на 50 эпохах. В последнем столбце указано, как изменилась средняя accuracy при увеличении эпох от 25 до 50 — чем ближе значение к зеленому, тем быстрее к лучшему решению с точки зрения метрики accuracy сходится алгоритм. Значения каждого столбца размечены тепловой картой независимо от значений в других столбцах.

Таблица 3.



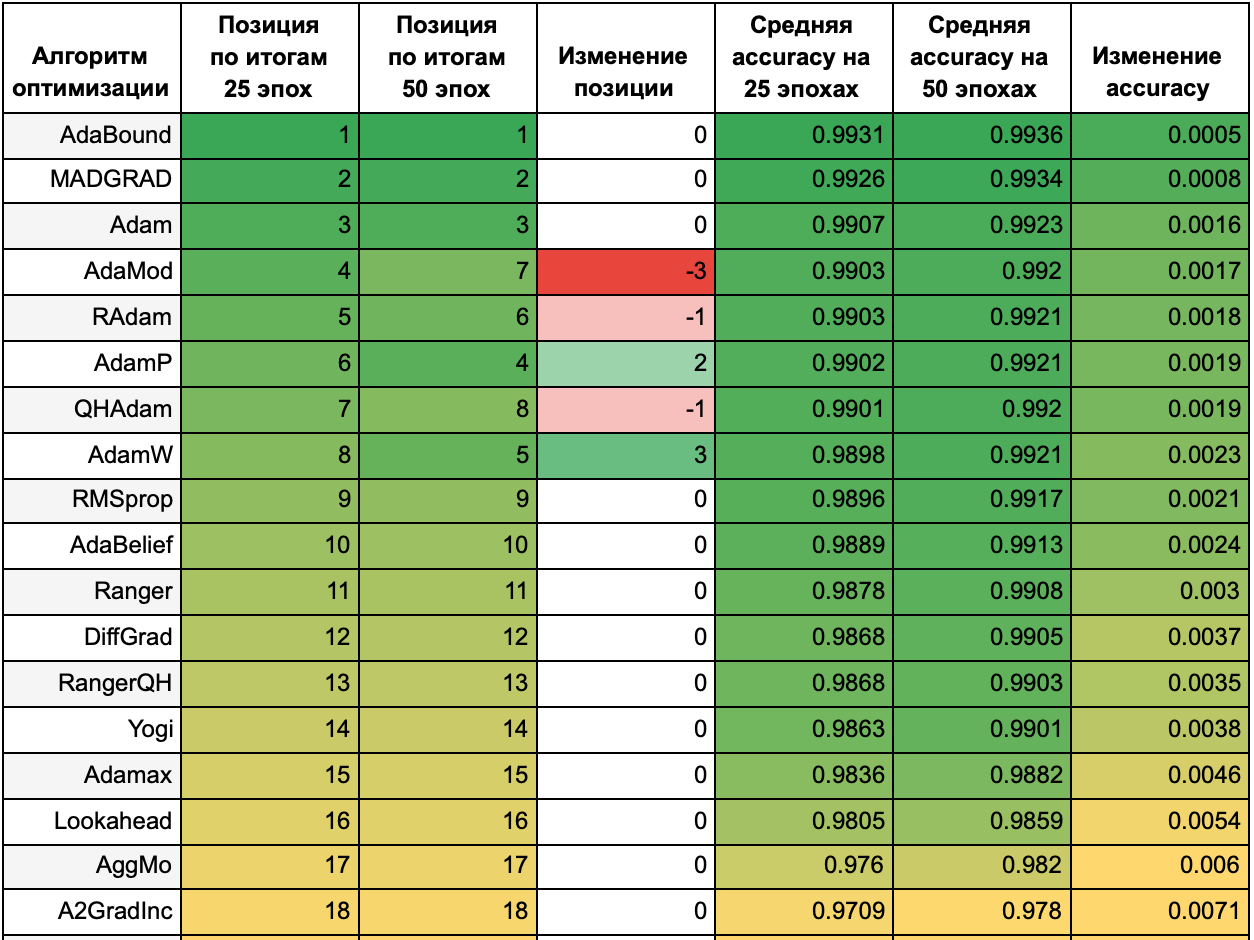
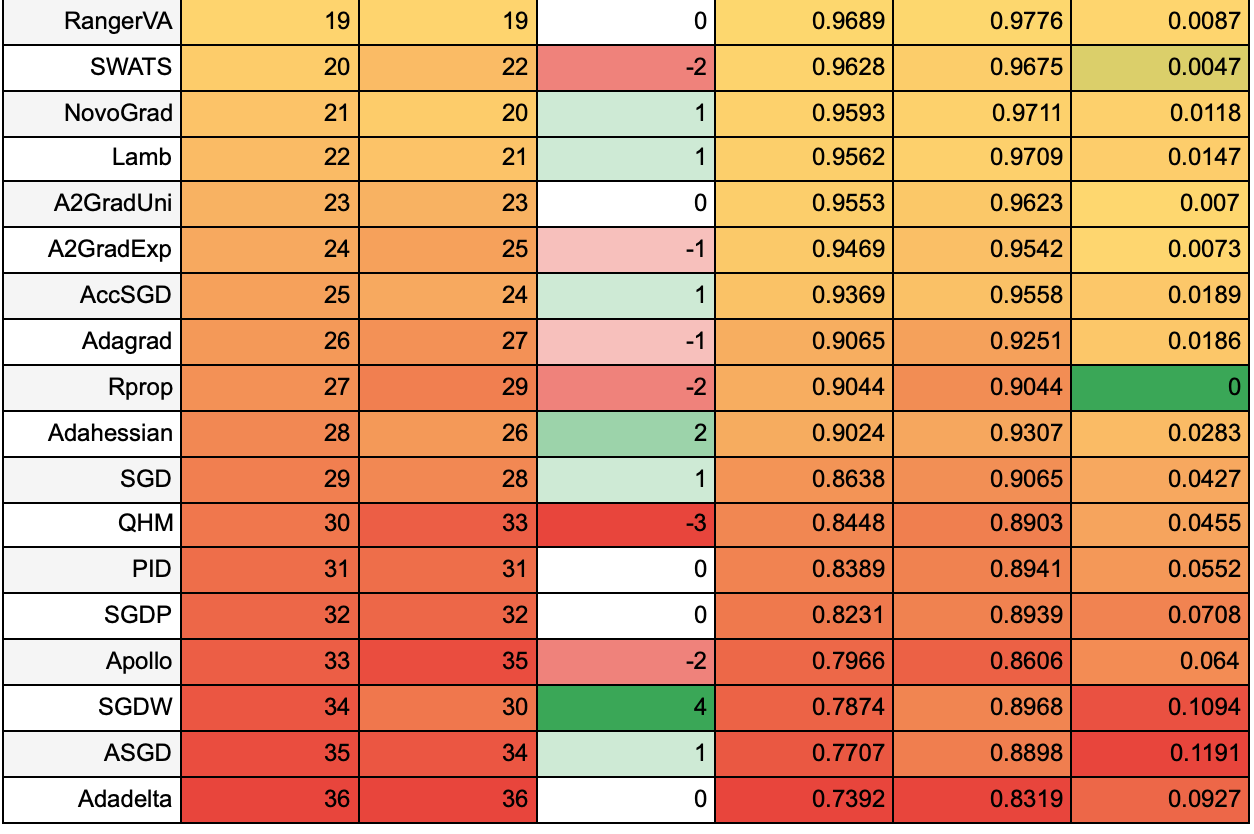
Из таблицы видно, что чем лучшие результаты показывал алгоритм на 25 эпохах, тем меньше его результаты изменились при увеличении эпох до 50. Однако, ни один из алгоритмов с худшими результатами не смог вырваться в лидеры. Среди лидеров вышли вперед алгоритмы AdamW и AdamP — выходит, им требуется больше времени, чтобы сойтись.

Сравнение с разными размерами батча

Посмотрим, как оптимизаторы ведут себя на разных размерах батча (8, 16, 32, 64, 128, 256) cо значениями learning rate 1e-2, 1e-3, 1e-4, 1e-5.

На части из алгоритмов, таких, как SGD, при уменьшении размера батча увеличивается точность даже на больших learning rate. Это связано с тем, что при большом размере батча происходит недостаточно обновлений, и часть из алгоритмов не успевает обучиться на 25 эпохах. На другой части алгоритмов такая ситуация возникает при уменьшении learning rate.

Ниже приведены примеры графиков accuracy для разных learning rate и размера батча, которые иллюстрируют эту ситуацию: так, алгоритм SGDW не успевает обучиться за 25 эпох даже при больших значениях learning rate, а алгоритм MADGRAD сходится быстрее, и ему начинает не хватать обновлений при learning rate = 1e-5.

Графики для алгоритма SGDW при разных размерах батча и фиксированном learning rate:



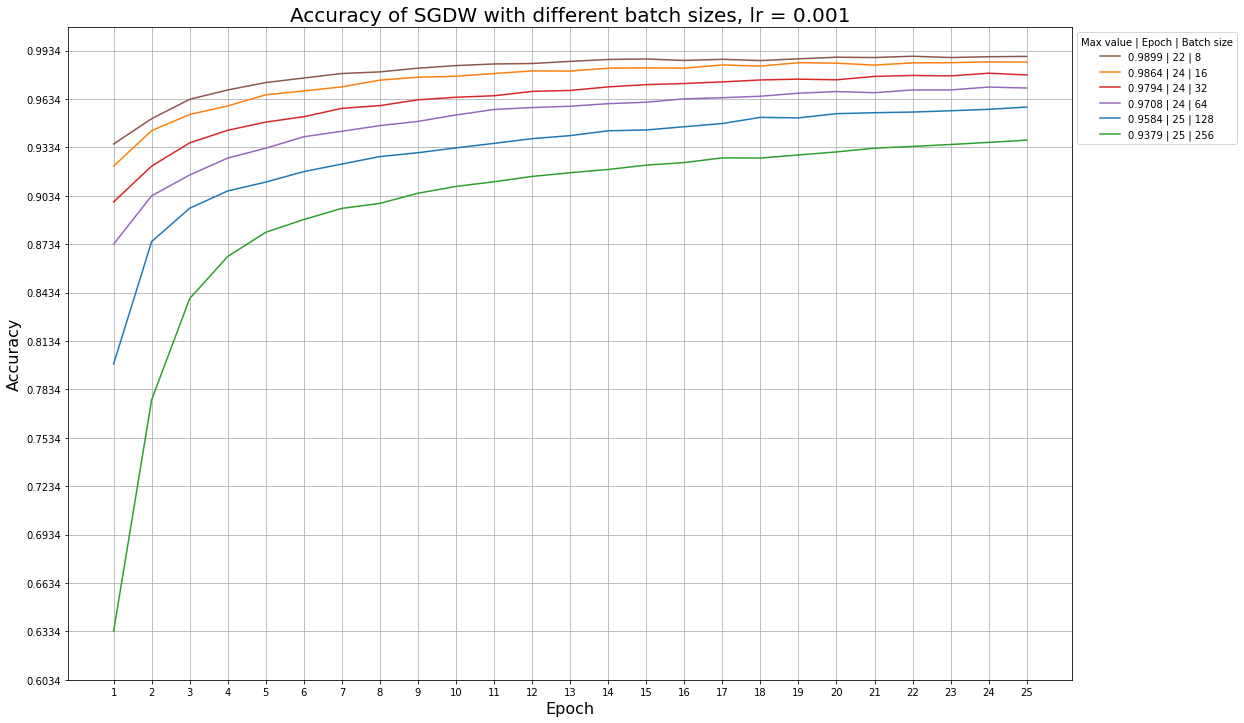
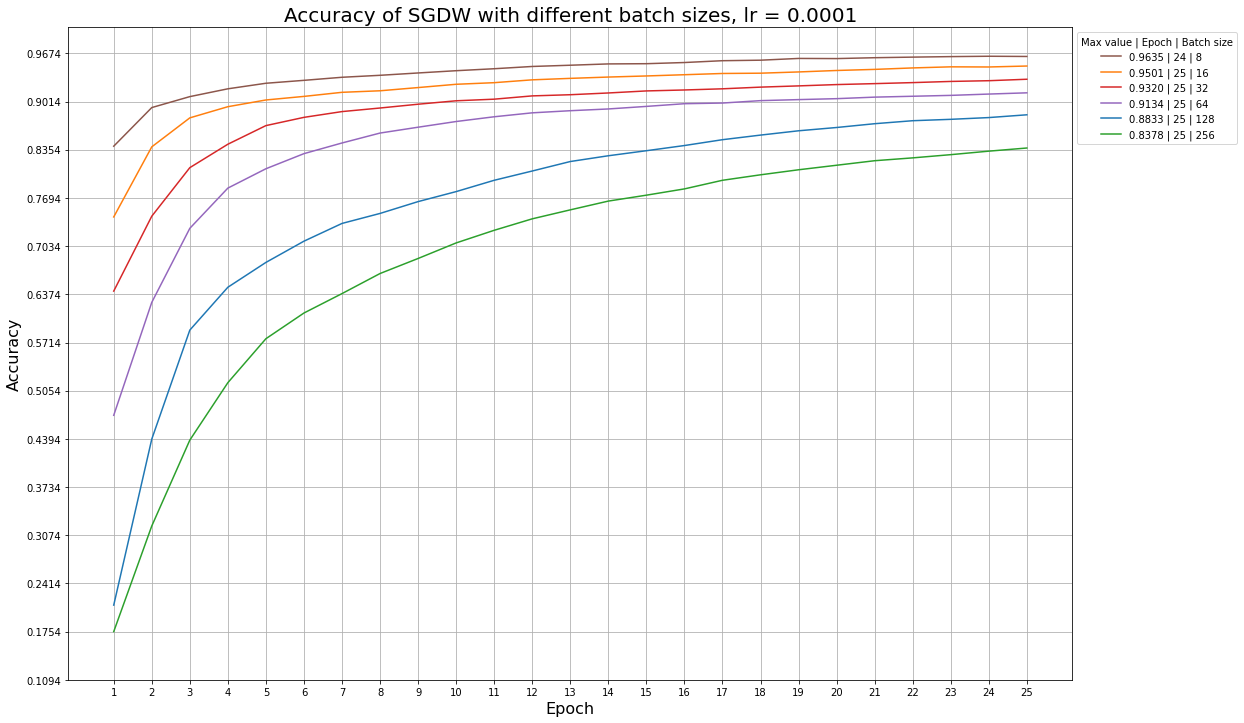
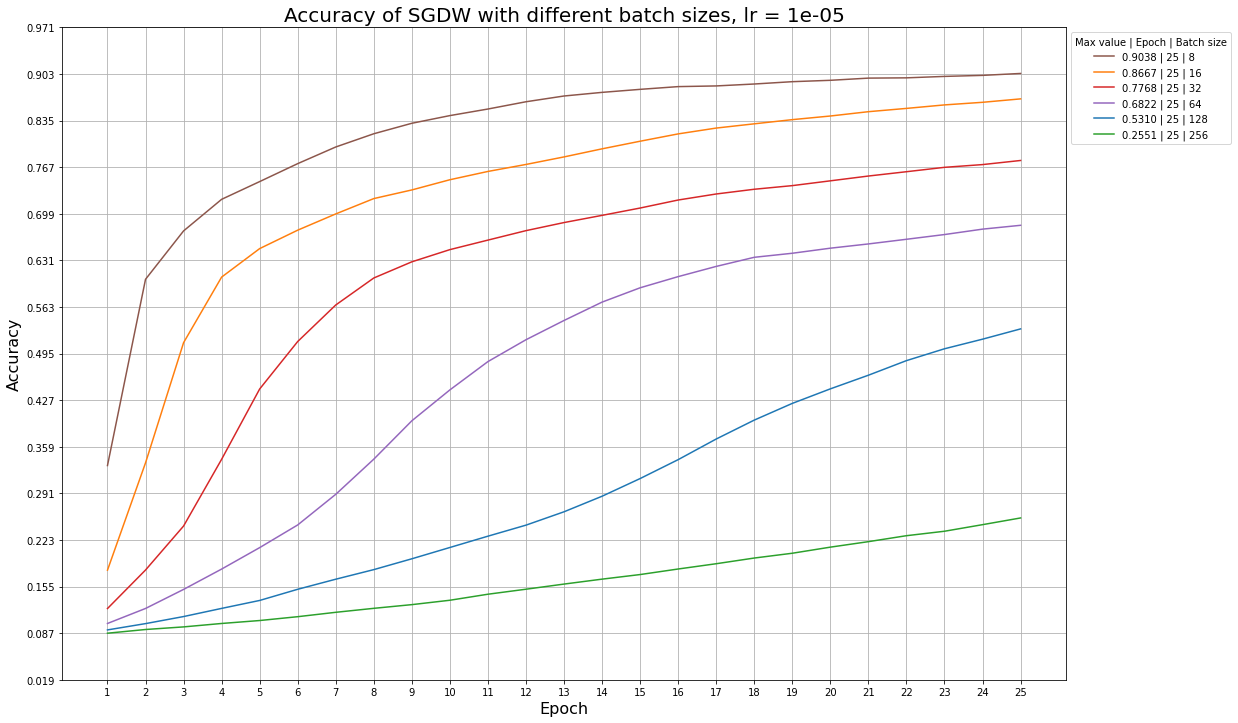
Графики для алгоритма MADGRAD при разных размерах батча и фиксированном learning rate:



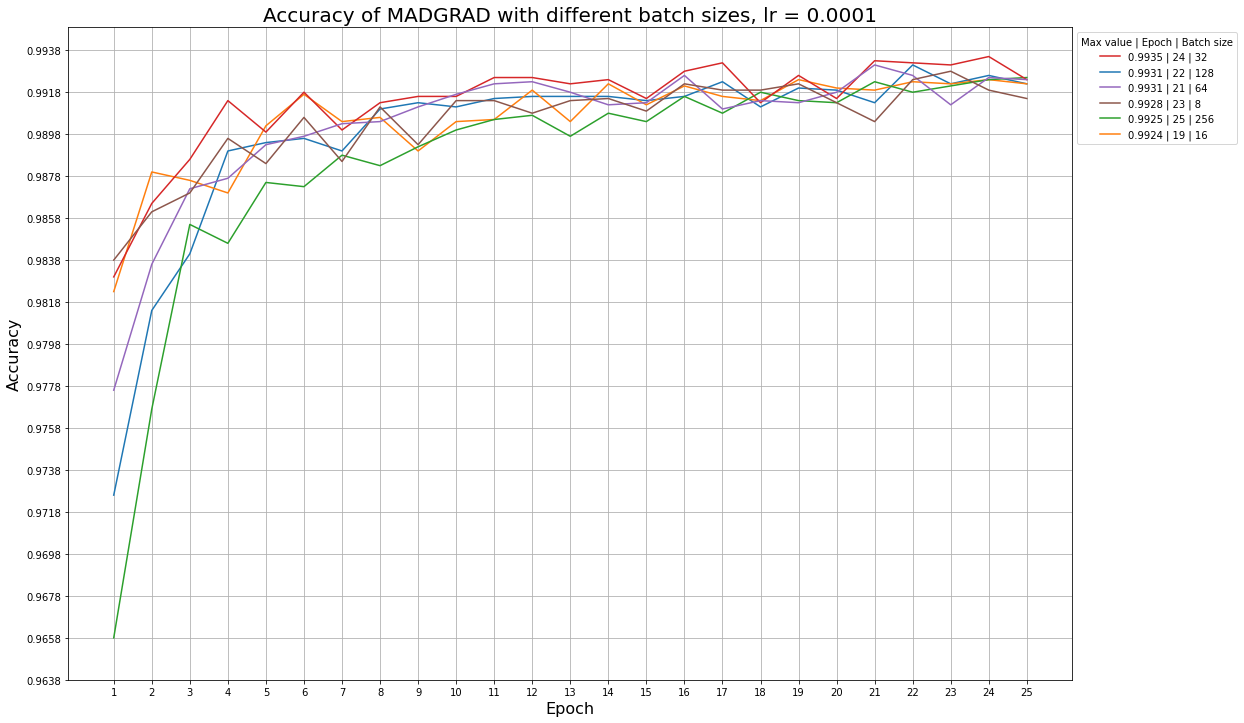
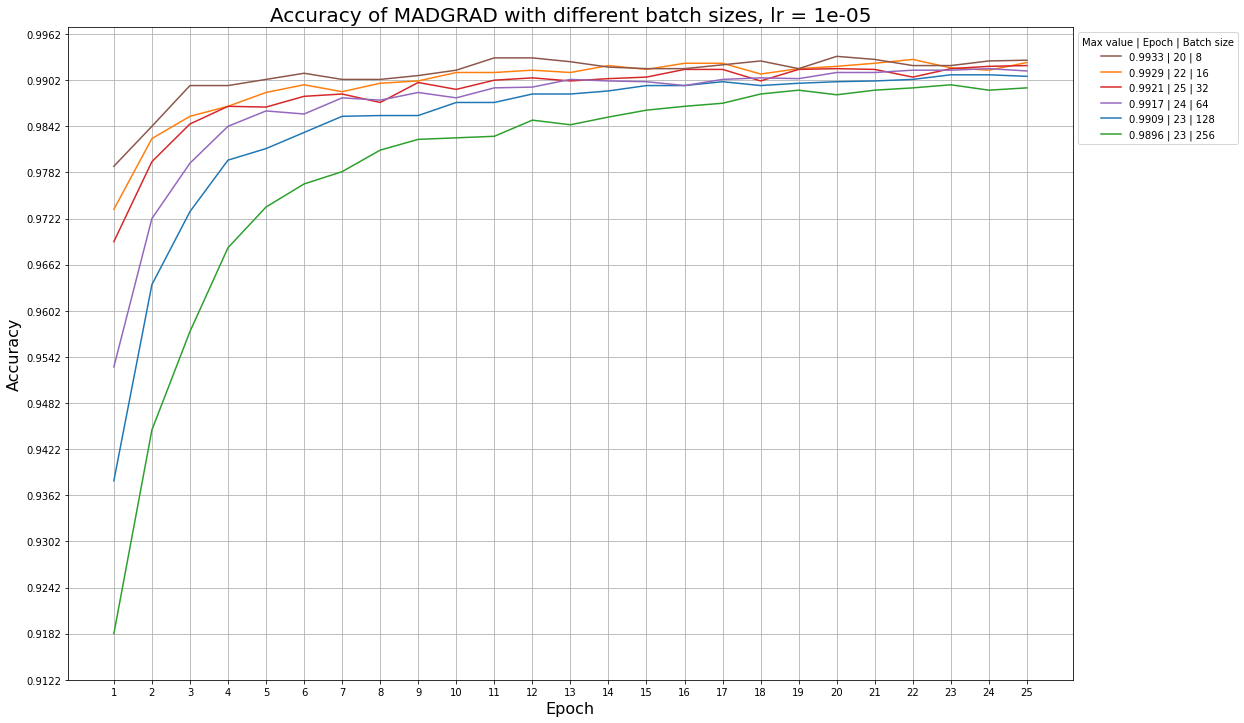
В таблице ниже все алгоритмы отсортированы по максимальной средней точности из предыдущего пункта. Для каждого алгоритма указан learning rate, начиная с которого accuracy обратно пропорциональна размеру батча:




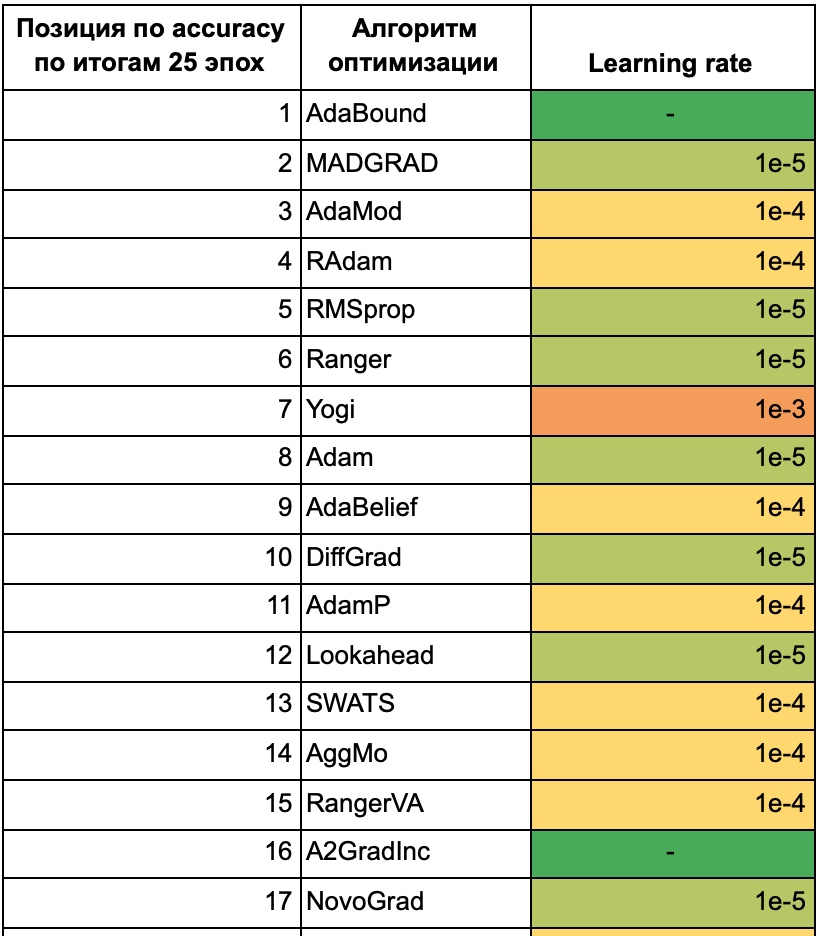
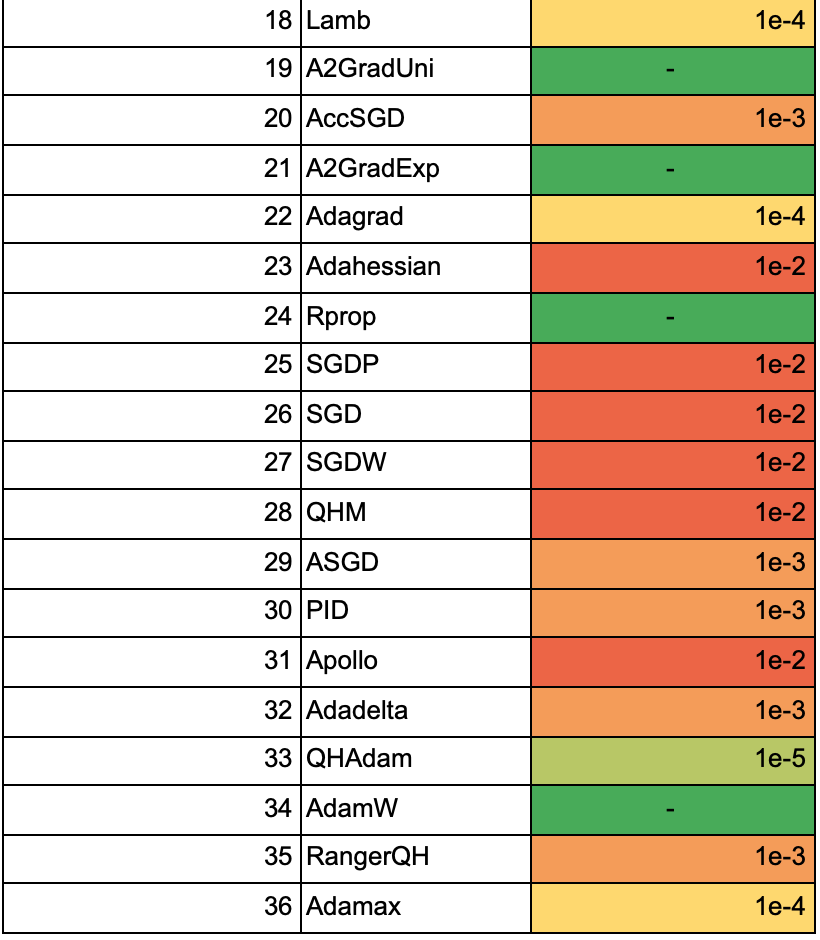
В таблице ниже указана средняя accuracy моделей, обученных с разными оптимизаторами, для каждого значения learning rate и размера батча для 25 эпох:



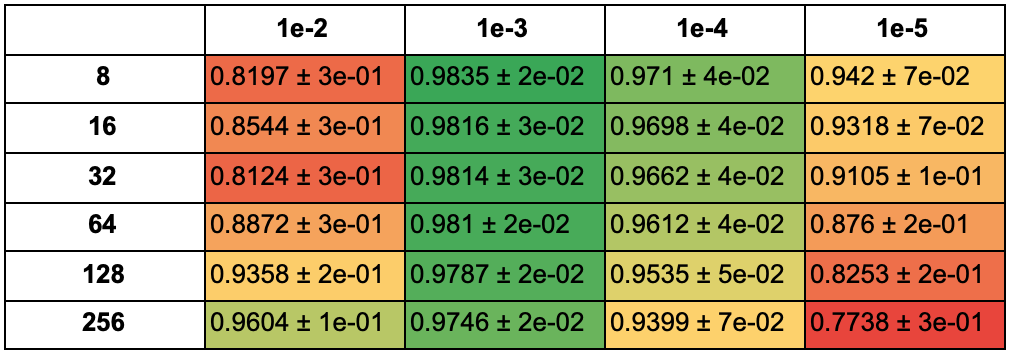
Для 50 эпох:


В этой таблице указана средняя accuracy среди 5 моделей с наибольшей accuracy для каждой фиксированной пары learning rate и размера батча для 25 эпох:


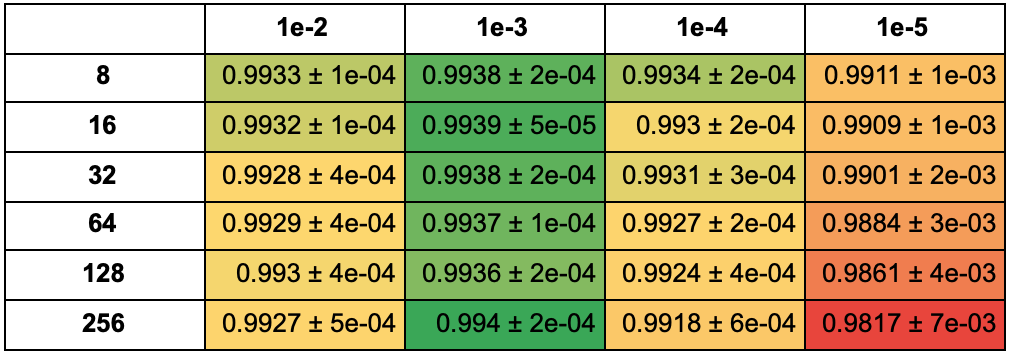
Для 50 эпох:


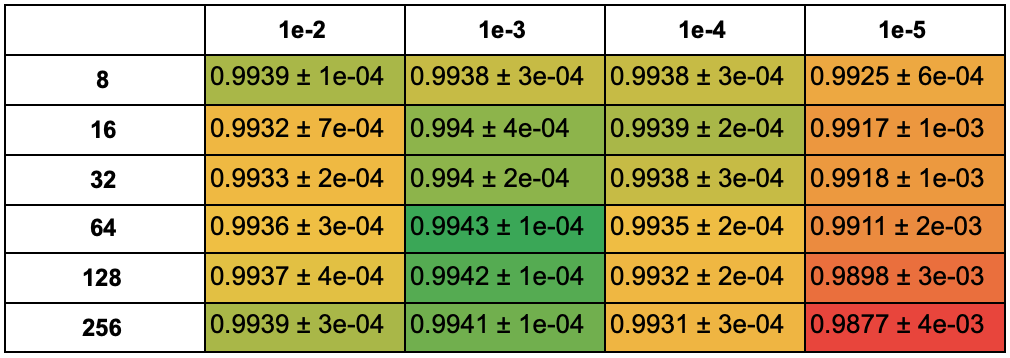
При learning rate = 1e-3, 1e-4 и 1e-5, чем меньше размер батча, тем больше средняя accuracy моделей. При learning rate = 1e-2 часть из алгоритмов ведет себя нестабильно. При learning rate = 1e-5 многим алгоритмам не хватило 25 эпох обучения.

Сравнение с разными расписаниями learning rate

Зафиксируем learning rate и размер батча и попробуем менять learning rate в зависимости от эпохи с разными стратегиями. Возьмем следующие 12 learning rate schedulers:

• StepLR(gamma = 0.1) со значениями step_size = 1, 2, 3: умножение learning rate на gamma каждые step_size эпох;
• ReduceLROnPlateau(factor=0.1) co значениями patience = 2, 3: если функция потерь не уменьшается в течение patience эпох, то learning rate умножается на factor;
• CosineAnnealingLR(T_max = 10, eta_min = 0);
• CosineAnnealingWarmRestarts(T_0 = 10, T_mult = 1, eta_min = 0);
• CyclicLR(base_lr = 1e-3, max_lr = 0.1) со значениями mode = ’triangular’, ’triangular2’, ’exp_range’;
  
• OneCycleLR(max_lr = 0.1) cо значениями anneal_strategy = 'cos' и 'linear';
  

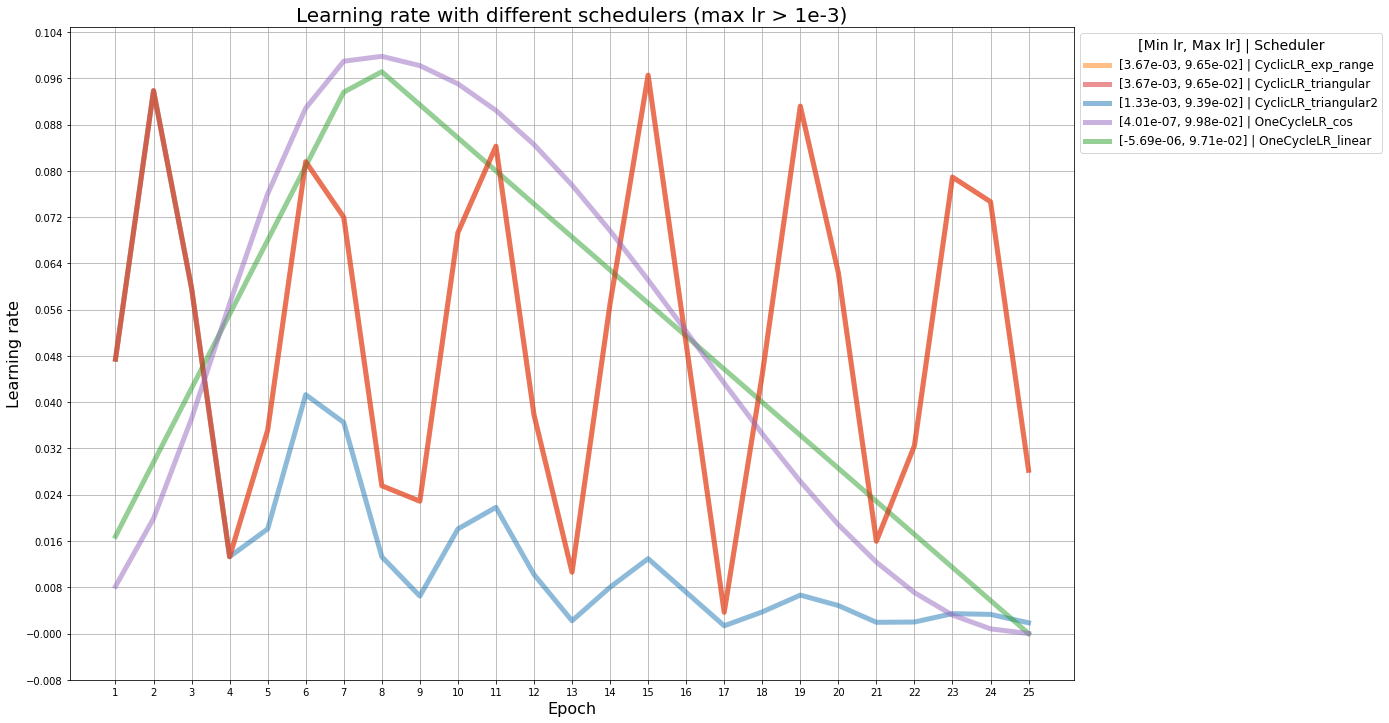
На графиках ниже изображено, как изменяется learning rate с разными расписаниями. В легенде указаны минимальный и максимальный learning rate для каждого расписания. Серая линия — участок наложения графиков ReduceLROnPlateau со значениями patience, равными 2 и 3, бордовые — участки наложения графиков CosineAnnealingLR и CosineAnnealingWarmRestarts.


Здесь наложились друг на друга CyclicLR с политиками triangular и exp_range, поэтому, дальше exp_range рассматриваться не будет.


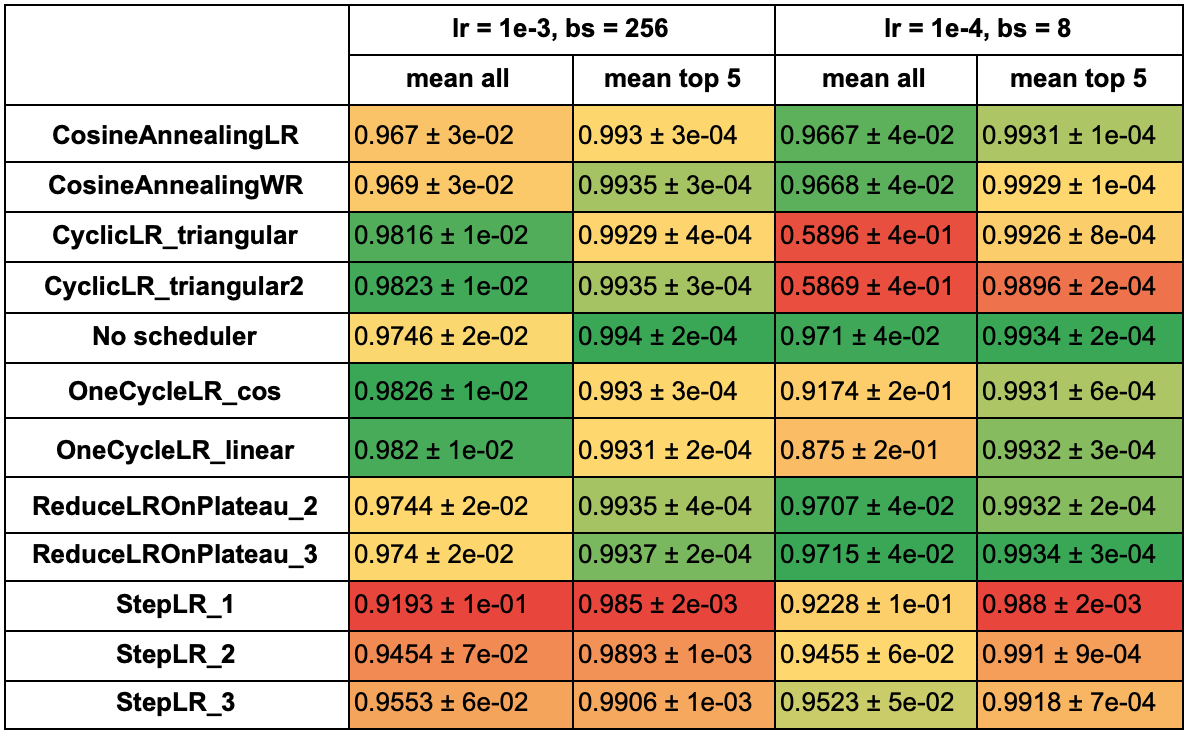
По таблице из предыдущего пункта возьмем параметры, при которых 5 лучших моделей набрали наибольшую среднюю accuracy (learning rate 1e-3 и размер батча 256) и также возьмем параметры одного из средних результатов (learning rate 1e-4, размер батча 8). В таблицах ниже отображены средняя accuracy и отклонение всех моделей с каждым из расписаний и средняя accuracy по 5 лучшим результатам.

В следующей серии

В следующей статье я расскажу про тот же эксперимент, но проведенный уже на реальной задаче — мультилейбловой классификации фото, сделанных на мобильный телефон. Будем благодарны вашему фидбеку о том, что можно было бы сделать лучше/понятнее/интереснее в этом эксперименте.