Вокруг нас появляется все больше различных устройств, систем, комплексов, платформ – технологических, информационных, киберфизических. Мы не задумываемся о том, как кофеварка варит кофе, робот-пылесос выбирает маршрут при уборке квартиры, система биометрической идентификации определяет человека на видеокадре, а портал государственных услуг обрабатывает наше заявление на получение справки об отсутствии судимости. Мы привыкаем к этим системам как к «черным ящикам», которые дают предсказуемый результат на выходе, не заботясь о том, как эти системы себя «чувствуют». Такой потребительский подход простителен пользователям, но совсем по-другому относятся к этому компании-разработчики и те, кто занимается эксплуатацией технологических систем. Для них и описан далее один из оригинальных методов поиска аномалий во временных рядах, т.е. состояний, по которым можно понять, что системе становится «плохо» (либо станет в ближайшем будущем).
Для эффективной эксплуатации сложных технологических систем нужны мониторинг и различные методы аналитики, позволяющие контролировать, управлять, упреждающе менять параметры. Мониторинг, как правило, обеспечивается типовыми инструментами (в большинстве случаев достаточно надежной системы сбора и визуализации данных). А вот для создания эффективных аналитических инструментов необходимы дополнительные исследования, эксперименты и хорошее знание предметной области. Как правило выделяют четыре основных вида аналитики данных [1]:
Описательная аналитика визуализирует накопленные данные, в том числе преобразованные для наглядности и интерпретируемости. Описательная аналитика - самый простой вид анализа, но и самый важный для применения других методов анализа.
С помощью диагностической аналитики исследуют причину возникновения событий в прошлом, при этом выявляются тренды, аномалии, наиболее характерные черты описываемого процесса, ищут причины и корреляции (взаимосвязи).
Прогнозная аналитика предсказывает вероятные результаты на основе выявленных тенденций и статистических моделей, полученных с помощью исторических данных.
Предписывающая аналитика позволяет получить оптимальное решение производственной задачи на основе прогнозной аналитики. Например, это может быть оптимизация параметров работы оборудования или бизнес-процессов, перечень мер по предотвращению аварийной ситуации.
Для прогнозной и предписывающей аналитики как правило используются методы моделирования, в том числе машинное обучение. Эффективность этих моделей зависит от качественной организации сбора, обработки и предварительного анализа данных. Перечисленные виды аналитики различаются как по сложности используемых моделей, так и по степени участия человека.

Сфер применения инструментов аналитики очень много - информационная безопасность, банковский сектор, государственное управление, медицина и многие другие предметные области. Часто один и тот же метод эффективно работает для разных предметных областей, поэтому разработчики систем аналитики создают универсальные модули, содержащие различные алгоритмы.
Для многих технологических систем результаты мониторинга можно представить в виде временных рядов [2]. Свойствами временного ряда являются:
привязка каждого измерения (сэмпла, дискрета) ко времени его возникновения,
равное расстояние по времени между измерениями,
возможность из данных предыдущего периода восстановить поведение процесса в текущем и последующих периодах.
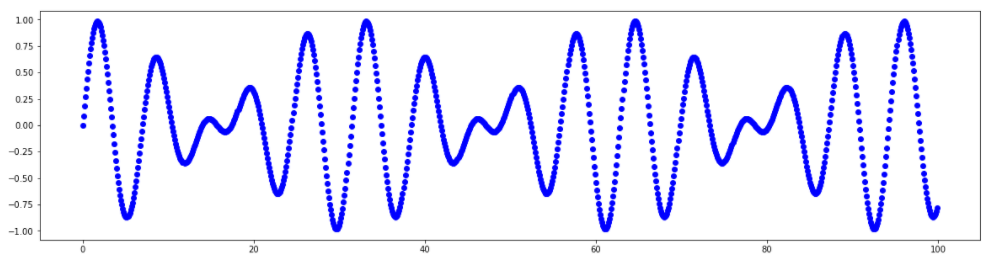
Временные ряды могут описывать не только численно измеримые процессы. Применение различных методов и архитектур моделей, включая глубокие нейронные сети, позволяет работать с данными из задач обработки естественного языка (NLP), компьютерного зрения (CV) и т.п. Например, сообщения в чате можно преобразовать в числовые векторы (эмбеддинги), которые последовательно появляются в определенное время, а видео представляет из себя ни что иное как матрицу чисел, изменяющуюся во времени.
Итак, временные ряды очень полезны для описания работы сложных устройств и часто используются для типовых задач: моделирование, прогнозирование, выделение признаков, классификация, кластеризация, поиск паттернов, поиск аномалий. Примеры такого использования: электрокардиограмма, изменение стоимости акций или валюты, значения прогноза погоды, изменение в объеме сетевого трафика, параметры работы двигателя и многое другое.
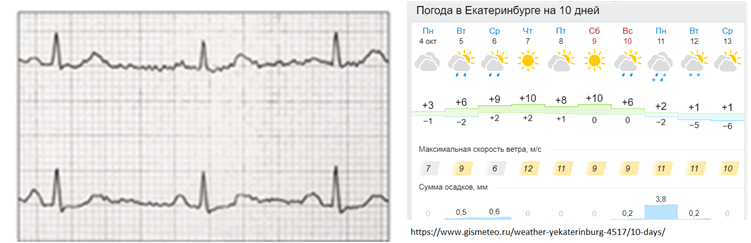
У временных рядов есть типовые характеристики, которые достаточно точно описывают характер временного ряда:
период - временной отрезок постоянной для всего ряда длины, на концах которого ряд принимает близкие значения,
сезонность - свойство периодичности (сезон=период),
цикл - характерные изменения ряда, связанные с глобальными причинами (например, циклы в экономике), нет постоянного периода,
тренд - тенденция к долгосрочному увеличению или уменьшению значений ряда.
Временные ряды могут содержать аномалии. Аномалия — это отклонение в стандартном поведении какого-то процесса. Алгоритмы машинного поиска аномалий используют данные о работе процесса (датасеты). В зависимости от предметной области в датасете могут быть аномалии разного вида. Принято различать несколько видов аномалий:
точечные аномалии, когда наблюдается отклонение в поведении в отдельных точках;
групповые аномалии, в которых аномально ведут себя группа точек, каждая из которых отдельно аномальной не является;
аномалии контекста, когда аномалия связана с внешними данными, не касающимися значений ряда (например, отрицательная температура на улице летом).
Точечные аномалии распознаются проще всего – это отдельные точки, в которых поведение процесса резко отличается от других точек. Например, можно наблюдать резкое отклонение значений параметра в отдельной точке.
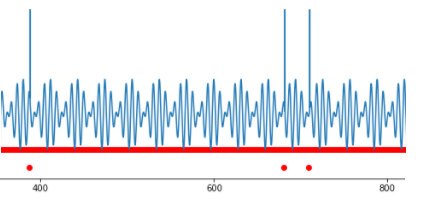
Такие значения называются «выбросы», они сильно влияют на статистические показатели процесса и их легко обнаружить, установив пороговые значения для наблюдаемой величины.
Сложнее обнаружить аномалию в ситуации, когда в каждой точке процесс ведет себя «нормально», но в совокупности значения в нескольких точках ведут себя «странно». К такому аномальному поведению можно отнести, например, изменение формы сигнала, изменение статистических показателей (среднее значение, мода, медиана, дисперсия), появление взаимной корреляции между двумя параметрами, небольшие или краткосрочные аномальные изменения амплитуды и так далее. И в этом случае задача заключается в распознавании аномального поведения параметров, которое нельзя выявить обычными статистическими методами.

Поиск аномалий очень важен. В одной ситуации надо данные очищать от аномалий, чтобы получать более реальную картину, в другой же ситуации аномалии должны внимательно исследоваться, так как могут свидетельствовать о возможном скором переходе устройства в аварийный режим.
Поиск аномалий во временных рядах непрост (нечеткое определение аномалии, отсутствие разметки, неочевидная корреляция). До сих пор SOTA алгоритмы по поиску аномалий во временных рядах имеют высокий уровень False Positive.
Вручную можно обнаружить только небольшое количество аномалий, в основном точечных, при наличии хорошей визуализации данных. Групповые аномалии сложнее обнаружить вручную, особенно если речь идет о большом количестве данных и анализе информации о нескольких устройствах. Также сложным для выявления является случай «аномалии во времени», когда нормальный по параметрам сигнал появляется в «неправильное» время. Поэтому при поиске аномалий во временных рядах целесообразно применять методы автоматизации.
Большой проблемой в поиске аномалий на реальных данных является то, что данные как правило не размечены, поэтому изначально строго не определено, что такое аномалия, нет правил для поиска. В таких ситуациях необходимо применять методы обучения без учителя (unsupervised learning), при этом модели самостоятельно определяют взаимосвязи и характерные законы в данных.
Используемые для поиска аномалий во временных рядах методы принято разделять на группы [3]:
proximity-based: выявление аномалии на основе информации о близости параметров или последовательности параметров фиксированной длины, подходит для выявления точечных аномалий и выбросов, но не позволит выявить изменения в форме сигнала,
prediction-based: построение прогнозной модели и сравнение прогноза и фактической величины, лучше всего применимо ко временным рядам с выраженными периодами, циклами или сезонностью,
reconstruction-based: методы, основанные на реконструкции фрагментов данных, используют восстановление (реконструкцию) фрагмента данных, поэтому может выявлять как точечные аномалии, так и групповые аномалии, в том числе изменения в форме сигнала.
Proximity-based методы ориентированы на поиск значений, существенно отклоняющихся от поведения всех остальных точек. Самый простой и наглядный пример реализации такого метода – контроль превышения заданного порога значений.
В prediction-based методах основная задача – построить качественную модель процесса, чтобы смоделировать сигнал и сравнить полученные смоделированные значения с исходными (истинными). Если предсказанный и истинный сигнал близки, то поведение считается «нормальным», а если значения в модели сильно отличаются от истинных, то поведение системы на этом участке объявляется аномальным.

Наиболее распространенные методы для моделирования временных рядов – SARIMA [4] и рекуррентные нейронные сети [5].
Оригинальный подход используется в reconstruction-based моделях – сначала модель обучают кодировать и декодировать сигналы из имеющейся выборки, при этом закодированный сигнал имеет гораздо меньшую размерность, чем исходный, поэтому модели приходится учиться «сжимать» информацию. Вот пример такого сжатия для картинок 32 на 32 пикселя в матрицу из 32 чисел.
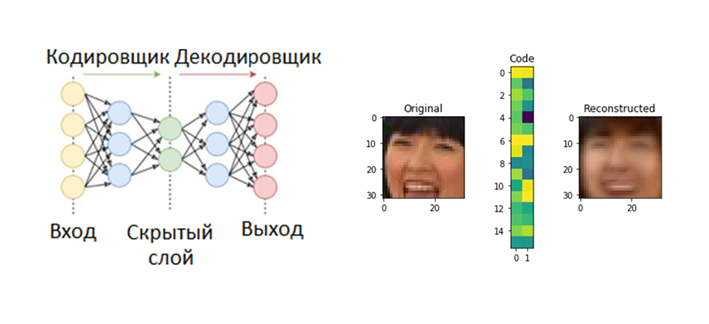
После обучения модели дают на вход сигналы, являющиеся отрезками исследуемого временного ряда, и если кодирование-декодирование проходит успешно, то поведение процесса считается «нормальным», в противном случае поведение объявляется аномальным.
Одним из недавно разработанных reconstruction-based методов, показывающих хорошие результаты в обнаружении аномалий, является TadGAN [3], разработанный исследователями из MIT в конце 2020 года. Архитектура метода TadGAN содержит в себе элементы автокодировщика и генеративных состязательных сетей.
![Рис.7. Архитектура TadGAN (из статьи [3]) Рис.7. Архитектура TadGAN (из статьи [3])](https://habrastorage.org/getpro/habr/upload_files/507/197/d04/507197d04b43daa9e8ff8441a284096d.png)
Ɛ действует как кодировщик, переводящий отрезки временных рядов x в векторы скрытого пространства z, а G – декодер, восстанавливающий из скрытого представления z отрезки временных рядов. Cx – критик, оценивающий качество восстановления G(Ɛ(х)), а Cz – критик, оценивающий похожесть скрытого представления z = Ɛ(х) на белый шум. Кроме того, действует контроль «похожести» исходного и восстановленного сэмплов с использованием L2 - меры по идеологии «Cycle consistency loss» (обеспечивает общую похожесть сгенерированных образцов на исходные сэмплы в GAN) [6]. Итоговая целевая функция - объединение всех метрик для оценки качества работы критиков Cx, Cz и меры похожести исходного и восстановленного сигнала.

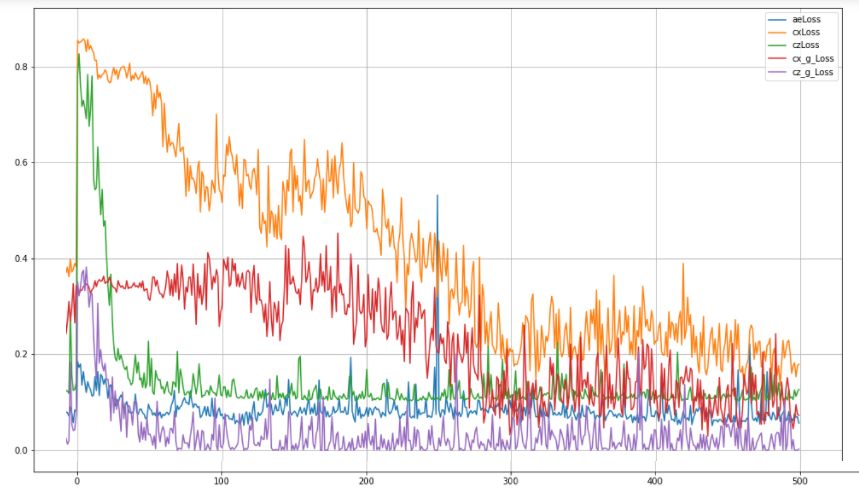
Для создания и обучения нейронной сети могут быть использованы различные стандартные пакеты (например, TensorFlow или PyTorch), имеющие высокоуровневое API. Пример реализации архитектуры, аналогичной TadGAN, с использованием пакета TensorFlow для обучения весов можно посмотреть в репозитории [7]. При обучении этой модели оптимизировались пять метрик:
aeLoss – среднеквадратичное отклонение между исходным и восстановленным временным рядом, т.е. разница между x и G(Ɛ(х)),
cxLoss – бинарная кросс-энтропия критика Cx, определяющего разницу между истинным отрезком временного ряда и искусственно сгенерированным,
cx_g_Loss – бинарная кросс-энтропия, ошибка генератора G(Ɛ(х)), характеризующая его неспособность «обманывать» критика Cx,
czLoss - бинарная кросс-энтропия критика Cz, определяющего разницу между скрытым вектором, который сгенерировал кодировщик Ɛ и белым шумом, обеспечивает похожесть скрытого вектора Ɛ(х) на случайный вектор, не давая модели «заучивать» отдельные паттерны в исходных данных,
cz_g_Loss – бинарная кросс-энтропия, ошибка генератора Ɛ(х), характеризующая его неспособность создавать скрытые векторы, похожие на случайные, и тем самым «обманывать» критика Cz.
После обучения модели проводится реконструкция отдельных отрезков исследуемого временного ряда и сравнение исходного и реконструированного ряда, которое может осуществляться одним из методов:
поточечное сравнение;
сравнение площадей кривых в заданной области вокруг каждого сэмпла (длина области - гиперпараметр);
Dynamic Time Warping [9].
Качество оценивается по F1-метрике для задачи бинарной классификации, «positive» (нулевая гипотеза) - есть аномалия, «negative» (альтернативная гипотеза) - нет аномалии.
Аномалия предсказана моделью, y_hat = 1 |
Модель предсказала отсутствие аномалии |
||
|
Аномалия есть y = 1 |
TP правильно предсказанная аномалия |
FN аномалия есть, но ее не нашли |
|
|
Аномалии нет y = 0 |
FP предсказали аномалию там, где ее нет |
TN аномалии нет и модель ее не видит |
|
Для демонстрации работы метода используем синтетический (искусственно сгенерированный) ряд без аномалий, являющийся суммой двух синусоид, значения которого меняются в диапазоне от -1 до 1

График этого ряда:
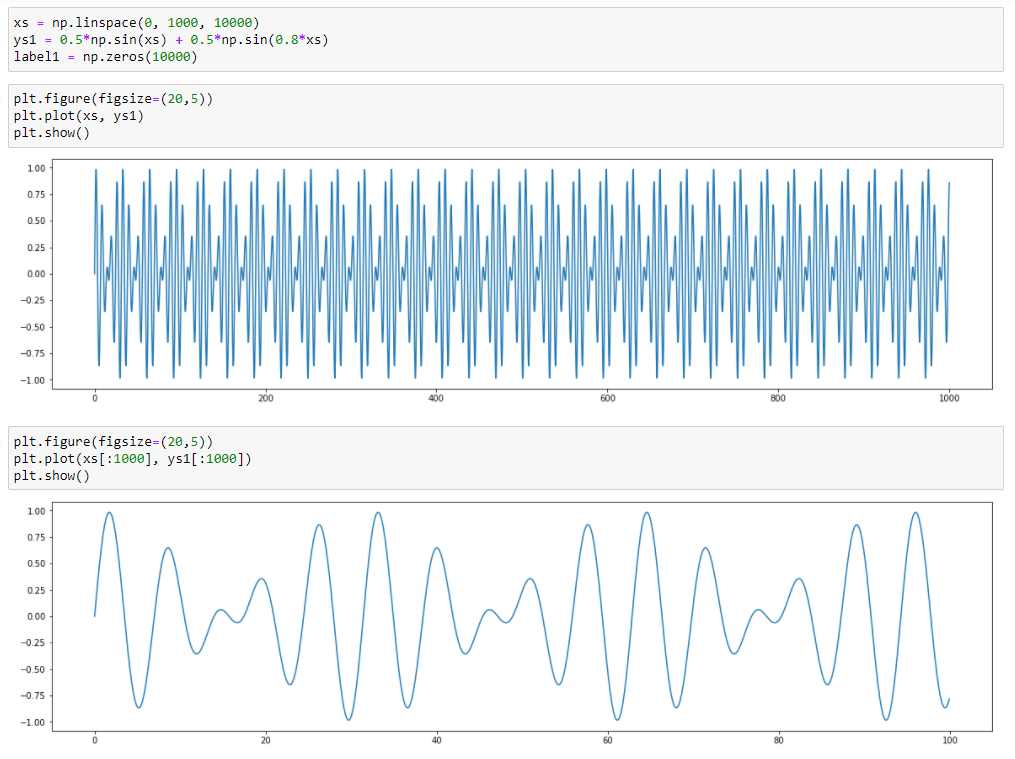
Восстановленный ряд с использованием TadGAN для разного количества эпох (4 и 80) выглядит так:
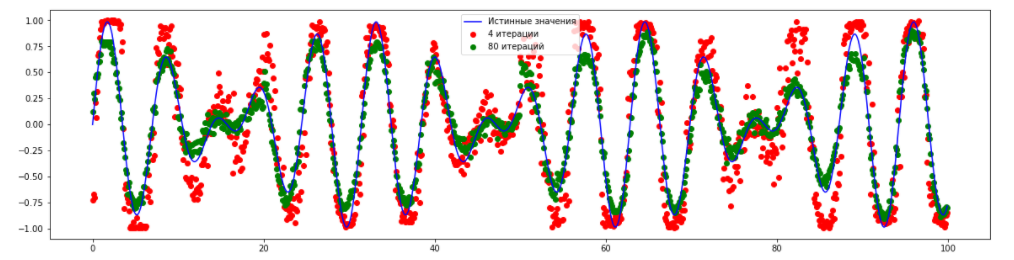
Видно, что модель достаточно точно научилась предсказывать основные закономерности в данных. Попробуем добавить различные аномалии в данных и затем обнаружить их с помощью модели TadGAN. Сначала добавим несколько точечных аномалий.

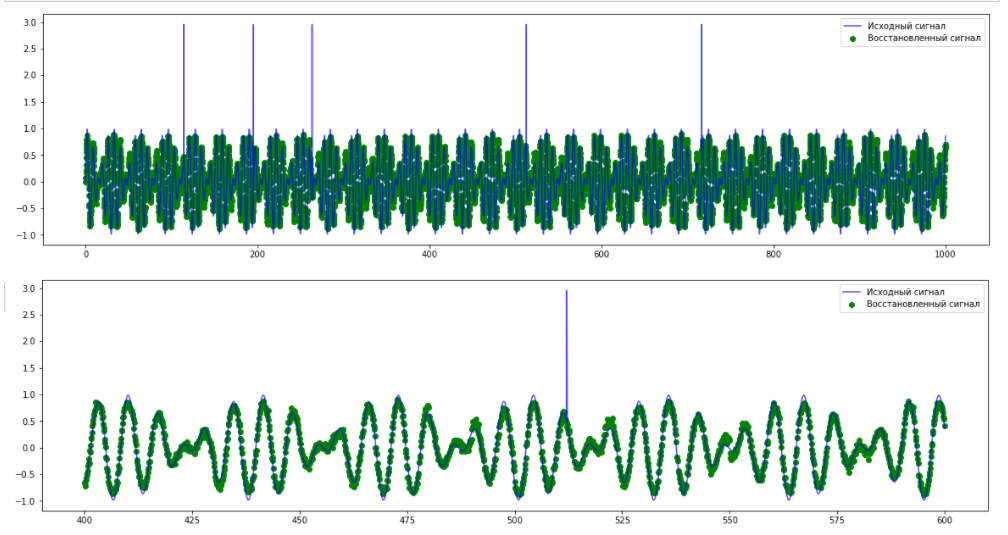
Из графика исходного и предсказанного сигналов видно, что модель не может восстановить «пики» аномальных значений, что с высокой точностью может использоваться для определения точечных аномалий. Однако в такой ситуации польза сложной модели TadGAN неочевидна – подобные аномалии можно обнаружить и с помощью оценки превышения пороговых значений.
Теперь рассмотрим сигнал с другим типом аномалии - периодический сигнал с аномальным изменением частоты. В этом случае нет превышения порога – с точки зрения амплитуды все элементы ряда являются «нормальными» значениями, и аномалия выявляется только в групповом поведении нескольких точек. В этом случае TadGAN также не может восстановить сигнал (как это видно на рисунке) и это может быть использовано в качестве признака наличия групповой аномалии.

На этих двух примерах проиллюстрирована работа метода. Читатель и сам может попробовать создать свои датасеты и проверить возможности модели в различных ситуациях.
Более сложные примеры датасетов можно найти в статье авторов метода TadGAN [3]. Там же приведена ссылка на библиотеку Orion, являющуюся разработкой специалистов MIT, которая с использованием машинного обучения распознает редкие аномалии во временных рядах, используя подход обучения без учителя (unsupervised learning).
В заключении отметим, что методов, использующих реконструирование сигнала (reconstruction-based) для обнаружения аномалии сейчас очень много, например в ресурсе arxiv.org десятки статей, описывающих различные модификации подхода с использованием автокодировщиков и генеративных состязательных сетей. Для каждой конкретной задачи целесообразно подбирать свою модель, с учетом требований задачи и знаний о предметной области.
Ссылки
«Что такое аналитика данных?», https://www.intel.ru/content/www/ru/ru/analytics/what-is-data-analytics.html
В.В. Домбровский. Эконометрика. http://sun.tsu.ru/mminfo/2016/Dombrovski/start.htm
“TadGAN: Time Series Anomaly Detection Using Generative Adversarial Networks”, https://arxiv.org/abs/2009.07769
“An Introductory Study on Time Series Modeling and Forecasting”, описание SARIMA https://arxiv.org/ftp/arxiv/papers/1302/1302.6613.pdf
Fundamentals of RNN, https://arxiv.org/abs/1808.03314
Cycle Consistency Loss, https://paperswithcode.com/method/cycle-consistency-loss
Библиотека для распознавания аномалий в сигналах, https://github.com/signals-dev/Orion
Алгоритм Dynamic Time Warping, https://towardsdatascience.com/dynamic-time-warping-3933f25fcdd
Комментарии (11)

adeshere
11.11.2021 01:13+11Свойствами временного ряда являются ...возможность из данных предыдущего периода восстановить поведение процесса в текущем и последующих периодах.
Вообще-то нет. Такое свойство есть только у некоторых временных рядов. Простейший контрпример - белый шум.
...равное расстояние по времени между измерениями
И это тоже чрезмерное упрощение.
Во-первых, существуют неэквидистантные временные ряды. Например, перепись населения стараются проводить регулярно, но не всегда получается. При этом набор значений величины популяции, измеренных в определенные годы - это самый что ни на есть типичный "временной ряд". В экономике сплошь и рядом встречаются переменные, которые измеряются (существуют) только в рабочие дни. Для таких величин обычный шаг между измерениями - 1 сут, но в конце недели - 3 сут, а на каникулах и праздниках еще больше. И такие увеличенные интервалы не всегда можно просто выбросить, особенно если речь идет о непрерывных производствах или фиксированных временных лагах. Например, если для производства товара А нужен скоропортящийся товар Б, на доставку которого надо 3 дня, то рост производства Б в понедельник и вторник отобразится в товаре А на третий рабочий день, а рост производства Б в пятницу - уже в понедельник (а это следующая точка, если выходные отброшены).
А в некоторых предметных областях существует такое понятие, как "пропущенное" измерение. Когда сломался прибор, и значения тупо нет. Или была экстремальная ситуация (помеха), и измеренное значение надо забраковать. В науках о Земле это случается сплошь и рядом. По существу, в результате опять-таки получаются неэквидистантные временные ряды, обрабатывать которые гораздо сложнее. Многие алгоритмы (например, БПФ) такое просто не предусматривают. Поэтому пробелы в таких рядах чаще всего интерполируются (заполняются) какими-то правдоподобными (но по сути - вымышленными) значениями. Тем самым ряд загоняется в прокрустово ложе эквидистантности... Проблема в том, что для адекватного заполнения пропущенных измерений нужна достаточно точная модель ряда (это необходимо, но не достаточно), а измерения часто как раз и проводятся для того, чтобы такую модель построить. Получается замкнутый круг.
Альтернативный подход состоит в том, чтобы закодировать пропуски особым образом и модифицировать каждый вычислительный алгоритм так, чтобы он обрабатывал эти пробелы каким-то разумным способом. Мы даже об этом статью написали, а вот тут можно скачать программу, в которой эти идем реализованы. Правда, она ориентирована на данные геофизического мониторинга в основном (поэтому чуть ли не половина алгоритмов нацелены на первичную обработку данных, поиск и выбраковку всевозможных дефектов и пр.), и у нее довольно высокий
порог вхождения.
По сути, это не просто "считалка", а комплекс из специализированной СУБД и пакета программ анализа временных рядов. Поэтому чтобы просто "покрутить" там какой-то сигнал, надо сперва его импортировать в базу. Впрочем, если вы все же решите попробовать - welcome, я с удовольствием помогу и отвечу на возникающие вопросы. Если вы работаете с интересными временными рядами, то есть шанс, что у нас найдутся общие интересы. Пишите мне в личку или на почту adeshere; мой почтовый домен переводится, как ИФЗ.РУ ;-).
Но написать я хотел не об этом, а о поиске аномалий в сигналах. На самом деле подобных методов - вагон и маленькая тележка. Причем в каждой предметной области они разные, так как исходят из собственных представлений об "аномалиях". Например, в исследованиях по прогнозу землетрясений бум таких методов был во второй половине прошлого века, как только стал доступен достаточный объем данных геофизического мониторинга. Кто только не занимался тогда прогнозом землетрясений! Однако в большинстве своем это были геофизики и геологи, хорошо умеющие работать в поле и закапывать электроды, а иногда и варганить аппаратуру, но не слишком натасканные в математическом смысле. Удивительно, но примерно за 30 лет напряженной работы (многие сотни статей!) никто в мире так и не обратил внимание, что определить понятие "аномалия" невозможно, пока не определено понятие "норма", и наоборот. Все упорно искали в сигналах исключительно "аномалии" (желательно перед самым землетрясением), и не менее упорно игнорировали вопрос - что есть "норма"? Не буду скромничать, но среди геофизиков одними из первых этим вопросом озаботилась наша группа. Мы проводили многолетние наблюдения в высокосейсмичном районе Таджикистана (Гармская экспедиция ИФЗ РАН). Как только вопрос был развернут в нужную сторону, сразу же выяснилось, что все наши ряды - это фликкер-шум. Кажется, ерунда - но для фликкер-шумового сигнала подавляющее большинство "аномалий", которые с таким упорством искали (и находили!) трудолюбивые геофизики, аномалиями совсем не являются. Для наших сигналов и изменения среднего, и всевозможные бухты, и всякая прочая "классика прогноза землетрясений" - это вовсе не аномалия, а самая что ни на есть "норма". Мораль очень простая: чтобы искать аномалии, надо сперва понять - что же такое норма (в геофизике это еще называют "проблемой фона").
Ну и в заключение - небольшое дополнение к статье, ради которого я и начал писать этот коммент. При поиске аномалий в нестационарных сигналах (а других при долговременном мониторинге практически не бывает) один из наиболее мощных подходов связан с методологией скользящего временного окна. В таком окне можно оценивать какой-то параметр-индикатор, коррелировать два сигнала, сравнивать свойства ряда в левой и правой половинах окна, и т.д. и т.п.
В частности, для ряда, приведенного на рис.4, эффективным индикатором будет преобладающая частота в спектре сигнала в пределах окна. Либо нормированная спектральная мощность на заданной частоте - она считается за О(N), что гораздо быстрее, чем полный спектр. (Правда, надо будет предварительно подкрутить частоту). Причем, оба таких индикатора будут в известной мере терпимы к шумам, а также нестационарным эффектам различного рода.
Вообще, в такой ситуации - когда характер возможных аномалий примерно понятен - вряд ли есть смысл использовать для их поиска какие-то обучаемые модели. Гораздо проще напрямую привязать алгоритм к критерию аномальности. Второе достоинство таких "прямых" алгоритмов - их результаты обычно гораздо интерпретабельнее, причем сразу же в терминах нужной предметной области.
Только в одной геофизике существует немеряное количество подобных "элементарных", но отлично работающих методов поиска аномалий в сигналах. Можно не одну монографию написать... Даже, пожалуй, не можно - а нужно: сейчас потыркался в памяти, а ссылок-то и нет на подхвате! Если вдруг кто-то за это возьмется - пишите, ваш труд, несомненно, будет оценен!! Я же пока ограничусь лишь ссылкой на нашу работу, к тому же не совсем тематическую. Но поскольку это лишь комментарий, а не самостоятельная статья, то надеюсь, что мне простят такое нахальство ;-)
Итого в заключение:
1) При поиске аномалий в сигналах начинать всегда надо с определения - что мы подразумеваем под аномалией, что мы ищем. Чем именно отличаются "норма" и "аномалия"? Даже если задача сформулирована максимально общо ("Найдите хоть что-нибудь!"), базой для поиска все равно будут два эти понятия. Без них никуда.
2) Если понятия "нормы" и "аномалии" введены, то для классификации состояния ряда в некоторый момент стоит прежде всего применять прямые (элементарные) алгоритмы, которые непосредственно вытекают из этих определений. Например, если "аномалия" - это выброс - то самый прямолинейный алгоритм будет основан на сравнении текущего значения ряда с локальным средним или же медианой. Если аномалия - это изменение персистентности, то элементарный прямой алгоритм может основываться на вычислении показателя Херста (или фрактальной размерности) в локальных окрестностях точки. И т.д. и т.п.
Нет, я не отрицаю потенциально возможную пользу методов с обучением. Но пока что не видел примеров их успешного применения в геофизике. Тогда как прямые элементарные методы эффективно работают на каждом углу.
3) Ну и последний совет - это обработка в скользящем окне. Это особенно интересно для существенно нестационарных сигналов (нестационарных не только по среднему, но и по другим показателям), но вполне эффективно и для обычных рядов.

CyberLympha Автор
16.11.2021 09:48+1Алексей, большое спасибо за столь развернутый комментарий, который сам достоин отдельной статьи на хабре! ????
Со многими утверждениями в комментарии мы безусловно согласны, они даже коррелируют с тем, что в нашей статье написано.
Неэквидистантные ряды конечно существуют, но многие практические методы (автокорреляция, сглаживание, SARIMA методы и упомянутое Вами БПФ) к ним применять невозможно.
Поэтому, как Вы правильно указали, для пропущенных значений применяют заполнение интерполяцией или какими-то другими методами, в том числе предложенным Вами.
И это отдельная большая задача, требующая, в том числе, хорошего понимания предметной области и анализируемого процесса.
Модель скользящего среднего неявно фигурирует среди описанных в статье методов.
Мы обязательно посмотрим рекомендованную Вами статью и попробуем программу.
Наша сфера интересов – аналитика для информационной безопасности и технологических процессов, но мы уверены, что в методах для геофизики содержатся интересные идеи в том числе для нашей предметной области.
Руководитель исследовательского центра ООО «Сайберлимфа» Чернышов Юрий свяжется с Вами по указанной электронной почте, и будем рады сотрудничеству!

adeshere
16.11.2021 19:03Модель скользящего среднего неявно фигурирует среди описанных в статье методов.
Да, этот класс моделей действительно трудно приспособить для работы с сигналами, в которых много пропущенных наблюдений. Но есть огромная куча других алгоритмов, которые позволяют строить вполне адекватные модели таких сигналов. Собственно, мы этим и занимаемся, изучая процессы в Земле.
Например, одна из типичных задач в самых разных прикладных областях - это построение модели сигнала с сезонной периодичностью, нелинейным трендом и "остаточной компонентой" (которая может быть квазислучайной, либо, наоборот, содержать все самое интересное). Экономисты придумали стопятьсот вариаций моделей типа АРСС, чтобы описывать такие ряды. Но по моему убеждению, гораздо более качественное и наглядное описание подобных сигналов можно построить, используя декомпозиционный подход. А именно, ряд сначала раскладывается на "элементарные составляющие" с очень простыми свойствами. Настолько простыми, что они превосходно описываются с помощью "элементарных моделей" типа среднесезонной функции. Которые, в отличие от АРСС, абсолютно индифферентны к пропущенным наблюдениям и другим дефектам сигнала. Затем каждая из таких составляющих изучается и, при необходимости, экстраполируется для прогноза. После чего остается только собрать сигнал из этих деталек. Такая схема работает очень стабильно, ведь параметры "элементарных моделей" оцениваются намного устойчивее, а в целом модель получается намного интерпретабельнее любых "черных ящиков", в которых скрыта самая продвинутая математика. Настолько продвинутая, что даже сам автор модели не всегда понимает, почему получилось именно так.
Вообще, основная проблема комплексных моделей, описывающих сразу весь сигнал в целом, состоит в том, что их оптимальность обычно доказана лишь для сигналов определенного вида. Однако (за редчайшими исключениями) ни один реальный сигнал нужными свойствами обычно не обладает. Но в таком случае о математической строгости можно забыть. Как писал один классик, некритическое использование таких моделей очень часто приводит к ошибочным выводам, которые особенно опасны потому, что имеют видимость математической точности и строгости [Урбах, 1963, с.7].
В качестве примера - альтернативы могу привести работу, в которой проводится декомпозиция рядов концентрации атмосферного CO2 на сезонный эффект, нестационарный тренд и квазистационарный остаток. (Ее текст в открытом доступе скоро появится на Researchgate либо могу выслать в личку). Да, у использованных в ней алгоритмов нет строгой теории. Но как замечено выше, добиться математической строгости при работе с такими сигналами в принципе невозможно.То есть это не баг исключительно предложенного подхода, а свойство почти любых технологий работы с экспериментальными временными рядами. Поэтому нет смысла на нем не зацикливаться, лучше взглянуть на плюсы. В данном примере я вижу ситуацию так: совершенно тривиальные процедуры вполне эффективно решают задачу, хотя на первый взгляд ряды имеют достаточно сложное поведение.
Неэквидистантные ряды конечно существуют, но многие практические методы (автокорреляция, сглаживание, SARIMA методы и упомянутое Вами БПФ) к ним применять невозможно.
Вот как раз корреляционные методы для некоторых неэквидистантных рядов прекрасно работают. А именно, если у нас есть эквидистантный временной ряд, из которого выброшена некоторая часть значений (т.н. пропусков наблюдений), то по оставшимся наблюдениям корреляционная функция строится без каких-то проблем. Ведь такая функция - это по сути матожидание от некоторой величины f(T), где T - это временной лаг между значениями сигналов X и Y. Обобщенную формулу для вычисления f(T) можно поэтому записать,как f(T)=fun( X(t), Y (t+T)), где fun - это некоторая функция, а время t пробегает все возможные значения в пределах некоторого интервала.
Очевидно, что при наличии пропусков данных в рядах X и Y некоторые пары значений {X(t), Y (t+T)} будут неполными - с одним или даже с двумя пропусками наблюдений. Однако для остальных моментов времени t оба значения X(t) и Y (t+T) будут известны. И мы вполне можем вычислить fun(T) хотя бы для таких пар.
Ну и теперь последний "философский" шаг. Вводя функцию fun (это не обязательно корреляция), мы изначально предположили, что нужное нам матожидание существует. Но в таком случае можно ожидать, что оценка этого матожидания по некоторому подмножеству наблюдений - это вполне осмысленная процедура. Просто мы используем для расчетов не всю генеральную совокупность, а только некоторую ее часть - ту, которая оказалась доступной.
Понятно, что на практике все сложнее. И что существуют ряды, выбросив из которых некоторую часть значений, мы получим сигнал с совершенно другими свойствами. Применяя подобный способ расчетов к таким рядам, можно получить на выходе черт знает что. Однако в большинстве случаев для возникновения таких проблем все же нужно достаточно неудачное стечение обстоятельств. Например, сигнал периодический, и пропуски в нем появляются с тем же самым периодом.
Но если сигнал квазислучайный, а моменты пропусков распределены хаотично, то описанный подход прекрасно работает. Больше того, при стремлении количества пропусков к нулю результаты сходятся к стандартным (которые ожидаются для сигнала без пропусков).
Например, для своих геофизических рядов мы прекрасно вычисляем и корреляции, и регрессии, и спектры (правда, не "быстрые") по данным с пропусками. И практически всегда получаем вполне осмысленный результат. Строго проверить такой результат невозможно, однако какие-то тесты все же имеются. Например, можно добавить в реальный сигнал дополнительные пропуски, а затем проанализировать зависимость целевой статистики от их количества. Да, это нестрогая процедура, но вполне рабочая и полезная. Вообще, на практике мне еще не встречались сигналы, в которых доля пропусков была бы относительно низкой (10-20%), и тем не менее, этот подход не работал бы. Хотя искусственные ряды с пропусками, "опровергающие" этот подход, строятся с полпинка, но вероятность встретить такую ситуацию при геофизическом мониторинге близка к нулю. Для этого надо, чтобы отказы прибора зависели от значения данных (например, не измеряются отрицательные значения). Если же моменты пропусков и измеряемая величина независимы, то все прекрасно работает.
Как я уже написал, у нас есть целый пакет программ, построенный на описанной парадигме. Кому интересно - можно посмотреть подробности в справке (конкретнее - раздел 3-I1). Конечно, использование такого подхода влечет определенные накладные расходы. Так, при вычислении функции fun надо для каждой пары значений {X(t), Y (t+T)} проверить - а нет ли среди них пропуска данных. И т.д. и т.п. Однако при долговременном мониторинге ряды данных чаще всего получаются не очень большие. Многие параметры до сих пор измеряются с частотой всего несколько раз в сутки. Даже если ряд имеет минутный опрос, это всего лишь полмиллиона значений в год. даже с учетом описанных "накладных расходов" обработка таких сигналов на современных персональных компьютерах выполняется за вполне разумное время.
В сухом остатке: понятно, что идеала нет и у любого подхода есть свои недостатки. Понятно, что выбрасывать ценные данные из-за нескольких пропущенных наблюдений - это ее дело. Я всего лишь хочу подчеркнуть, так называемое "обязательное заполнение пропусков" вовсе не является обязательным. Почти всегда существует альтернатива, и часто - не просто рабочая, но и имеющая свои преимущества.

mattroskin
11.11.2021 08:32А пробовали вы применять методы анализа рядов из финансов? По предсказанию котировок очень много литературы
dMac
11.11.2021 13:51+4И очень мало толку, ИМХО

CyberLympha Автор
15.11.2021 15:58Частично согласны) Тем не менее, алгоритмы-роботы, использующие различные методы анализа временных рядов, а также обучение с подкреплением (Reinforcement Learning) давно и эффективно работают в финансовом анализе, в том числе - торговле акциями.

CyberLympha Автор
15.11.2021 15:57У нашей компании основное направление это информационная безопасность. Также мы применяем свои разработки для анализа данных технологических устройств.
Но, как мы написали в статье, многие методы можно применять для разных отраслей, и финансовая сфера действительно создает много хороших задач для аналитики.
Поскольку мы не специализируемся в области финансового анализа, то цели применять методы для анализа финансовых данных у нас нет.
Но мы открыты к сотрудничеству и совместным проектам и готовы оказать поддержку компаниям, которые интересуются применением методов аналитики для анализа финансовых данных.

rotor
15.11.2021 14:28Немного дополню. На предыдущей работе делал систему детектирования атак на основании определения аномалий в трафике по логам веб сервера.
Основная концепция такая: атакующий будет стараться прикинуться добропорядочным пользователем, но распределения отдельных параметров трафика всегда очень специфичны и ему не известны. Т.е. невозможно подделать распределения.
Этот метод хорошо сработал и позволял почти молниеносно реагировать.
А алгоритмически смысл очень простой:
Подход в лоб, в виде анализ статистических характеристик (таких как статистические моменты) работает плохо и неустойчиво.
Но, информационные характеристики существенно обогащают понимание закономерностей и дают устойчивые результаты.
Под информационными характеристиками я имею ввиду такие вещи, как энтропии, взаимную информацию между отдельными рядами, информационные расстояния (дивергенции) и т.п.
Плюс по сравнению с нейросетевыми подходами: во-первых скорость и простота реализации. Во-вторых интерпретируемость и возможность очень чётко понять в какой из систем что пошло не так.
CyberLympha Автор
17.11.2021 09:21Все что можно сделать без машинного обучения – надо делать без машинного обучения )
Описанный Вами подход понятен и наверняка эффективен. Было бы интересно узнать метрики качества за какой-то продолжительный период.
Но важно отметить, что сейчас методы атак становятся все более изощренными, поэтому арсенал для защиты тоже необходимо развивать и применять методы, которые самообучаются в окружающей среде.


punzik
А что будет, если во входные данные добавить шум? До какого уровня сигнал/шум оно будет работать?
CyberLympha Автор
Шум в анализируемом сигнале всегда ухудшает извлечение полезной информации.
Если в сигнале преобладает шум, то ряд становится нестационарным и из него невозможно извлечь полезные сведения.
Убедиться в нестационарности можно, например, с использованием критерия Дики-Фуллера.
На практике часто применяются методы очистки от шума (например, алгоритмы сглаживания или автокодировщик-денойзер).