Как узнали возраст Вселенной?

В 1929 году американский астроном Эдвин Хаббл обнаружил, что галактики удаляются друг от друга. Поделив расстояние между ними на скорость удаления, можно вычислить, как давно они были в одной точке. Это грубая оценка возраста Вселенной.

График зависимости скорости от расстояния в оригинальной работе Хаббла

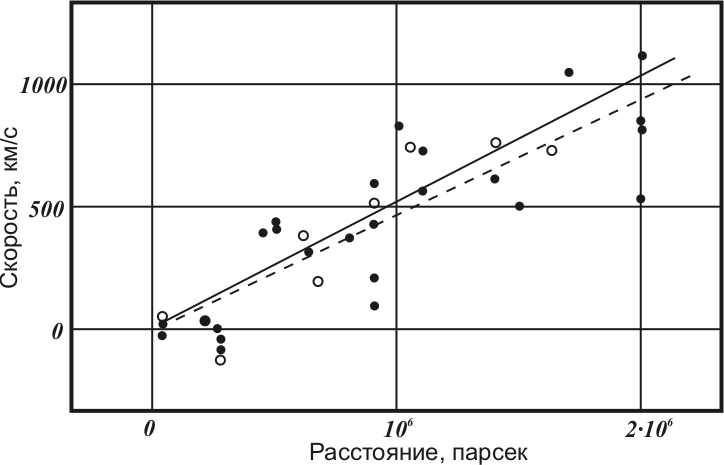
Физик Лоуренс Краусс в одной из своих лекций так говорил о Хаббле:

"Как видите, он был хорошим ученым, потому что провёл прямую линию через набор точек" (см. “Возникновение Вселенной”)

Вычисляем возраст Вселенной в R

Исходные данные

Попробуем почувствовать себя настоящими учеными, проведя прямую линию через набор точек. Для начала загрузим данные Freedman et al. (2001) по расстоянию (Distance, Mpc) до 36 сверхновых звезд типа Ia, а также по скорости удаления (Velocity, km/s) этих сверхновых, полученные при помощи космического телескопа "Хаббл". Данные доступны в пакете lava:

library(lava)
data(hubble)  
str(hubble) 

## 'data.frame':    36 obs. of  3 variables:
$ v    : num  9065 12012 15055 16687 9801 ...
$ D    : num  135 159 199 239 117 ...
$ sigma: num  2.3 3.1 2.8 2.8 3.4 2.9 3.1 2.2 3.4 2.7 ...
- attr(*, "labels")= chr  "Velocity (km/s)" "Distance (Mpc)" "sigma"

Строим диаграмму Хаббла с помощью базовой графики в R

plot(hubble$D, hubble$v, axes = FALSE, pch = 20, col = "blue",
		xlim= c(0,500), ylim = c(0, 30000),
		main = "", xlab = "", ylab = "") 
axis(1, at = seq(0, 500, by = 100), labels = seq(0, 500, by = 100))
axis(2, at = x <- seq(0, 3e4, by = 1e4),
		labels = expression(0, 1 %% 10^4, 2 %% 10^4, 3 %*% 10^4))
title(main = "Диаграмма Хаббла \n для сверхновых типа Ia",
		xlab = "Расстояние, Мпк",
		ylab = "Скорость, км/с")
abline(lm(hubble$v~hubble$D - 1), col = "red", lwd = 2)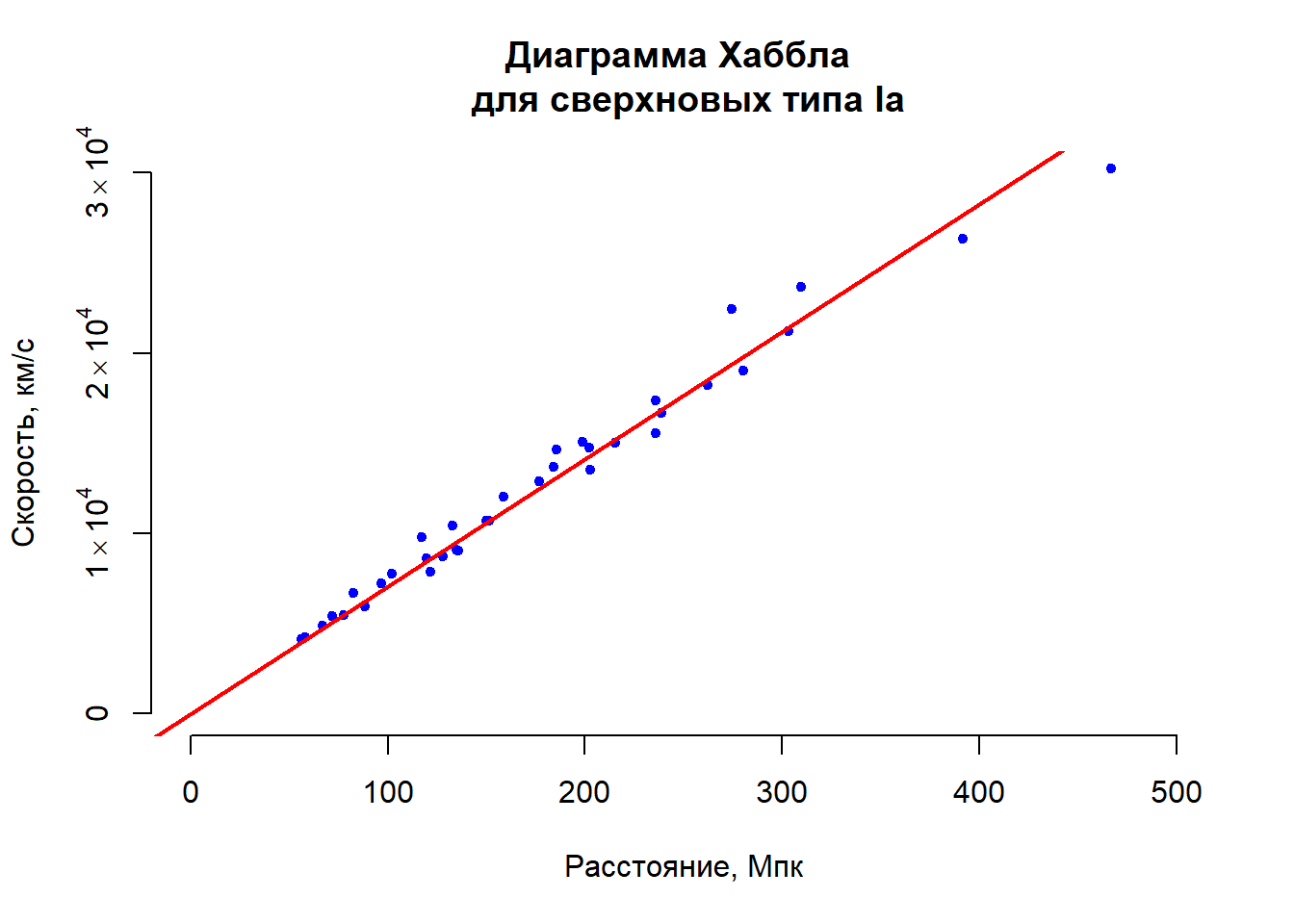

Вычисляем постоянную Хаббла при помощи простой линейной регрессии

fit <- lm(hubble$v~hubble$D - 1)

Смотрим результат:

summary(fit)
## 
## Call:
## lm(formula = hubble$v ~ hubble$D - 1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2748.6  -329.6   127.4   703.3  3020.8 
## 
## Coefficients:
##          Estimate Std. Error t value Pr(>|t|)    
## hubble$D  70.6672     0.8385   84.28   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1012 on 35 degrees of freedom
## Multiple R-squared:  0.9951, Adjusted R-squared:  0.995 
## F-statistic:  7103 on 1 and 35 DF,  p-value: < 2.2e-16

Как видим, оцененное значение постоянной Хаббла составило 70.667 км/с на мегапарсек. Это означает, что галактики, находящиеся на расстоянии 100 мегапарсек, удаляются от нас со скоростью ~7000 км/с. Постоянная Хаббла имеет размерность, обратную времени и выражается обычно в км/с на мегапарсек. Один мегапарсек – это 3.09∗10^19 км.

Один мегапарсек:

mpc <- 3.09 * 10^19
mpc

## [1] 3.09e+19

Секунд в одном году:

ysec <- 60^2*24*365.25
ysec

## [1] 31557600

Возраст Вселенной в секундах:

age <- 1/(fit$coefficients[[1]]/mpc)
age

## [1] 4.372608e+17

Возраст Вселенной в годах:

age/ysec
## [1] 13855957106

Или в млрд лет:

age/ysec/10e8
## [1] 13.85596

Итак, мы определили, что возраст Вселенной составляет ~ 13.86 миллиардов лет.

Из биографии Эдвина Хаббла: Будущий астроном мало занимался математикой, а трудности с правописанием не оставляли его до конца жизни. В возрасте 25 лет Эдвин не мог финансово помогать семье. Он не знал, чем хочет заниматься, у него даже не было девушки. Только в возрасте 40 лет Хаббл написал свою первую статью, в которой сформулировал свой закон. Эдвин учился на юриста, но стал выдающимся астрономом, работающим у телескопа в военной форме. Высокомерный Хаббл враждовал с коллегами, но дружил с одним астрономом – представительницей Гарварда Сесилией Пейн, которую называл "лучшим мужчиной Гарварда".

Вселенная Кеплера соответствовала Солнечной системе, Гершель расширил ее до размеров галактики, а во вселенной Хаббла наша галактика стала всего лишь маленькой точкой среди миллиардов других галактик. Он первым в мире осознал, насколько огромна Вселенная.