Постановка задачи

Имется связанный граф. Необходимо найти оптимальный путь начинающийся и заканчивающийся в данной точке, также необходимо посетить подмножество вершин графа.

Для решения данной задачи, сначала найдём минимальные расстояния между всеми необходимыми для посещения вершинами и остальными с помощью алгоритма Дейкстры. Затем будем искать минимальную сумму расстояний изменяя порядок посещения вершин.

Эту задачу можно встретить и на практике. Например, поиск маршрута для полета квадрокоптера-курьера.

Реализация графа

Граф с N вершинами будет храниться в матрице размера NxN.

По умолчанию зададим граф показанный на рисунке ниже (это делается для облегчения отладки):

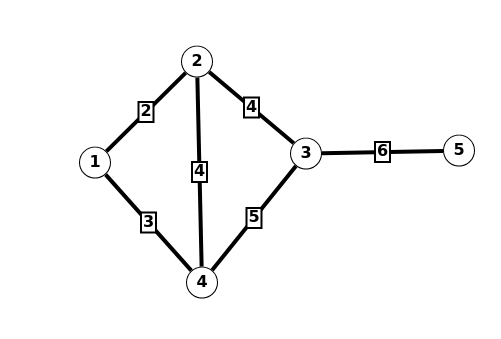
Graph.h:

#ifndef GRAPH_H
#define GRAPH_H

#include <iostream>
#include <iomanip>

using namespace std;

class Graph {
private:
    int n;                          // количество вершин графа
    int** data;                     // данные о ребрах графа: -1 - отсутствует ребро; >0 - расттояние между вершинами i и j
    
public:
    Graph(int n);                   // создание графа с n вершинами
    Graph();                        // граф по умолчанию
    int** Get_data() const;         // данные о графе
    int Get_n() const;              // количество вершин графа

};

ostream& operator<<(ostream& os, const Graph& g);

#endif

Graph.cpp:

#include "Graph.h"

Graph::Graph() {
    this->n = 5;
    data = new int*[5];
    for (int i = 0; i < 5; i++) {
        data[i] = new int[5];
    }

    // граф по умолчанию
    data[0][0] = 0;    data[0][1] = 2;    data[0][2] = -1;    data[0][3] = 3;    data[0][4] = -1;
    data[1][0] =2;     data[1][1] = 0;    data[1][2] = 4;     data[1][3] = 4;    data[1][4] = -1;
    data[2][0] = -1;   data[2][1] = 4;    data[2][2] = 0;     data[2][3] = 5;    data[2][4] = 6;
    data[3][0] = 3;    data[3][1] = 4;    data[3][2] = 5;    data[3][3] = 0;    data[3][4] = -1;
    data[4][0] = -1;   data[4][1] = -1;   data[4][2] = 6;     data[4][3] = -1;   data[4][4] = 0;
}

// создание графа с n вершинами
Graph::Graph(int n) {
    this->n = n;
    data = new int*[n];
    for (int i = 0; i < n; i++) {
        data[i] = new int[n];
    }
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            cout << "Input " << i << '-' << j << ": ";
            cin >> data[i][j];
            data[j][i] = data[i][j];
        }
    }
}

// данные о графе
int** Graph::Get_data() const {
    int** d = new int*[n];
    for (int i = 0; i < n; ++i) {
        d[i] = new int[n];
        for (int j = 0; j < n; ++j) {
            d[i][j] = data[i][j];
        }
    }
    return d;
}

// количество вершин графа
int Graph::Get_n() const { return n; }

// вывод графа
ostream& operator<<(ostream& os, const Graph& g) {
    int** d = g.Get_data();
    
    for (int i = 0; i < g.Get_n(); i++) {
        for (int j = 0; j < g.Get_n(); j++) {
            os << setw(4) << d[i][j] << ' ';
        }
        os << endl;
    }
    return os;
}

Реализация пути

Путь хранится в виде вектора, так как он представляет из себя последовательность вершин, также я храню длину всего пути. Реализуем функции добавления в конец пути одной вершины и другого пути (это будет использоваться дальше при переборе порядка вершин обхода).

Path.h:

#ifndef PATH_H
#define PATH_H

#include <iostream>
#include <set>
#include <vector>

using namespace std;

class Path {
private:
    vector<int> path;                   // путь
    int length;                         // длина пути

public:
    Path(int start);
    Path& operator= (const Path& p);
    vector<int> Get_path() const;       // путь
    int Get_length() const;             // длина пути
    void push_back(int v, int l);       // добавление вершины в конец
    void push_back(Path p);             // добавление пути в конец

};

ostream& operator<<(ostream& os, const Path& p);

#endif

Path.cpp:

#include "Path.h"

Path::Path(int start) {
    path.push_back(start);
    length = 0;
}

Path& Path::operator=(const Path& p) {
    path = p.Get_path();
    length = p.Get_length();
    return *this;
}

// путь
vector<int> Path::Get_path() const { return path; }

// длина пути
int Path::Get_length() const { return length; }

// добавление вершины в конец
void Path::push_back(int v, int l) {
    path.push_back(v);
    length += l;
}

// добавление пути в конец
void Path::push_back(Path p) {
    for (size_t i = 0; i < p.Get_path().size(); ++i) {
        int last = path[path.size() - 1];
        if (last != p.Get_path()[i]) {
            path.push_back(p.Get_path()[i]);
        }
    }
    length += p.Get_length();
}

ostream& operator<<(ostream& os, const Path& p) {
    size_t n = p.Get_path().size();
    for (size_t i = 0; i < n; i++) {
        os << p.Get_path()[i] + 1;
        if (i != n - 1) {
            os << "->";
        } else {
            os << " (";
        }
    }
    os << p.Get_length() << ')' << endl;
    return os;
}

Алгоритм Дейкстры

Обозначим все вершины бесконечностью, это будет означать, что вершина ещё не посещена, а начальную 0. Очевидно, что расстояние до самой себя равно 0. Теперь найдем расстояние из исходной точки в соседние, затем отметим её. Далее на каждом шаге находим минимальную не отмеченную точку и находим сумму с соседними, не отмеченными и сравниваем ее со значением вершины, если полученное расстояние меньше, то заменяем его.

Реализация алгоритма Дейкстры и решения задачи коммивояжёра

Алгоритм Дейкстры мы уже разобрали, но при его выполнении я также сразу сохраняю кратчайший путь от данной вершины к другим. Если вес вершины оказался больше, чем новый, то кроме нового веса, мы также заменяем путь: он будет равен пути к предыдущей вершине плюс сама вершина.

Все пути я записываю в словарь, ключом является вершина, а значением массив путей (i-ый элемент соответсвует кротчайшему пути до (i+1)-ой вершины).

После выполнения алгоритма Дейкстры с помощью next_permutation я перебираю порядок посещения вершин и нахожу путь минимальной длины.

Solution.h:

#ifndef SOLUTION_H
#define SOLUTION_H

#include "Graph.h"
#include "Path.h"
#include <iostream>
#include <limits>
#include <vector>
#include <map>
#include <algorithm>

using namespace std;

class Solution {
private:
    Graph graph;                                // граф

public:
    Solution(const Graph& g);
    Path* Dijkstra(int v, Path* data);          // алгоритм Дейкстры
    Path calc(vector<int> v, int start);        // вычисление оптимального пути

};

#endif

Solution.cpp:

#include "Solution.h"

Solution::Solution(const Graph& g) {
    graph = g;
}

// алгоритм Дейкстры
Path* Solution::Dijkstra(int v, Path* data) {
    data = (Path*)calloc(graph.Get_n(), sizeof(Path));      //пути от вершины v до других вершин графа
    int distaces[graph.Get_n()];                            //минимальное расстояние от вершины v до других
    int out[graph.Get_n()];                                 //посещенные вершины
    for (int i = 0; i < graph.Get_n(); ++i) {
        if (i == v) {
            distaces[i] = 0;
            data[i] = Path(v);
        } else {
            distaces[i] = numeric_limits<int>::max();
        }
        out[i] = 0;
    }

    int min = numeric_limits<int>::max(), index = -1;
    do {
        min = numeric_limits<int>::max();
        for (int i = 0; i < graph.Get_n(); ++i) {
            if ((out[i] == 0) && (distaces[i] < min)) {
                min = distaces[i];
                index = i;
            }
        }
        if (min != numeric_limits<int>::max()) {
            for (int i = 0; i < graph.Get_n(); ++i) {
                if (graph.Get_data()[index][i] > 0) {
                    int temp = min + graph.Get_data()[index][i];
                    if (temp < distaces[i]) {
                        distaces[i] = temp;
                        data[i] = data[index];
                        data[i].push_back(i, graph.Get_data()[index][i]);
                    }
                }
            }
            out[index] = 1;
        }
    } while (min < numeric_limits<int>::max());

    return data;
}

// вычисление оптимального пути
Path Solution::calc(vector<int> v, int start) {
    map<int, Path*> distaces;
    Path* temp = (Path*)calloc(graph.Get_n(), sizeof(Path));
    temp = Dijkstra(start, temp);
    distaces[start] = temp;
    for (size_t i = 0; i < v.size(); ++i) {
        temp = Dijkstra(v[i], temp);
        distaces[v[i]] = temp;
    }

    Path p = Path(start);
    sort(v.begin(), v.end());
    for (size_t i = 0; i < v.size(); ++i) {
        int last = p.Get_path()[p.Get_path().size() - 1];
        p.push_back(distaces[last][v[i]]);
    }
    int last = p.Get_path()[p.Get_path().size() - 1];
    p.push_back(distaces[last][start]);
    next_permutation(v.begin(), v.end());

    do {
        Path temp = Path(start);
        for (size_t i = 0; i < v.size(); ++i) {
            int last = temp.Get_path()[temp.Get_path().size() - 1];
            temp.push_back(distaces[last][v[i]]);
            if (temp.Get_length() > p.Get_length())
                break;
        }
        int last = temp.Get_path()[temp.Get_path().size() - 1];
        temp.push_back(distaces[last][start]);

        if (temp.Get_length() < p.Get_length()) {
            p = temp;
        }
    } while (next_permutation(v.begin(), v.end()));

    return p;
}

Итоги

Данное решение далеко от идеального, необходимо как минимум сделать многопоточность при переборе порядка вершин. Также в дальнейшем я оптимизирую алгоритм Дейкстры, уменьшив его сложность (O(n²)) с помощью Фибоначчиевой кучи (O(n log(n))).

Проект задачи Вы можете скачать на GitHub.