Аннотация

В настоящее время глубокие нейронные сети (DNN) стали основным инструментом для решения задач машинного обучения в широком спектре областей, включая компьютерное зрение, НЛП и речевое общение. Между тем, в важном случае гетерогенных (неоднородных – как по типу, форме, так и по структуре) табличных данных преимущество DNN перед частными аналогами остается сомнительным. В частности, нет достаточных доказательств того, что механизмы глубокого обучения позволяют создавать методы, которые превосходят деревья решений с выбором по росту градиента (GBDT), которые часто являются лучшим выбором для табличных задач. В этой статье мы представляем ансамбли нейронных решений без внимания (NODE), новую архитектуру глубокого обучения, предназначенную для работы с любыми табличными данными. Кратко, предлагаемая архитектура NODE обобщает ансамбли деревьев решений с забыванием (без памяти), но извлекает выгоду как из сквозной оптимизации на основе градиентов, так и из возможностей многоуровневого обучения иерархическому представлению. Проведя обширное экспериментальное сравнение с ведущими пакетами GBDT на большом количестве табличных наборов данных, мы демонстрируем преимущество предлагаемой архитектуры NODE, которая превосходит конкурентов по большинству тестовых задач. Мы используем реализацию NODE с открытым исходным кодом PyTorch и считаем, что она станет универсальной платформой для машинного обучения на основе табличных данных.

1. Введение

Недавний рост исследований глубоких нейронных сетей (DNN) привел к существенному прорыву в решении большого числа задач машинного обучения в области компьютерного зрения, обработки естественного языка, распознавания речи, обучения с подкреплением (Гудфеллоу и др., 2016). Как оптимизация на основе градиента с помощью обратного распространения (Румельхарт и др., 1985), так и обучение по иерархическому представлению, по-видимому, имеют решающее значение для повышения производительности машинного обучения для этих задач.

Хотя превосходство глубоких архитектур в этих областях несомненное, машинное обучение для табличных данных все еще не в полной мере воспользовалось возможностями DNN. А именно, современная производительность в задачах с табличными разнородными данными часто достигается с помощью «неглубоких» моделей, таких как деревья решений с градиентным усилением (GBDT) (Фридман, 2001; Чен и Гестрин, 2016; Ке и др., 2017; Прохоренкова и др., 2018). В то время, как важность глубокого обучения табличным данным признается сообществом ML, и многие работы посвящены этой проблеме (Zhou & Feng, 2017; Yang et al., 2018; Miller et al., 2017; Lay et al., 2018; Feng et al., 2018; Ke et al., 2018), предлагаемые подходы DNN не всегда превосходят современные мелкие модели с заметным отрывом. В частности, насколько нам известно, до сих пор не существует универсального подхода DNN, который, как было показано, систематически превосходит ведущие пакеты GBDT (например, XGBoost (Chen & Guestrin, 2016)). В качестве дополнительного доказательства большое количество соревнований Kaggle ML с табличными данными по-прежнему выигрывается с помощью неглубоких методов GBDT (Harasymiv, 2015). В целом, на данный момент не существует доминирующего решения для глубокого обучения для задач с табличными данными, и мы стремимся убрать этот пробел в нашей статье.

Мы представляем ансамбли нейронных решений без внимания (NODE), новую архитектуру DNN, предназначенную для работы с табличными задачами. Архитектура NODE частично вдохновлена недавним пакетом CatBoost (Прохоренкова и др., 2018), который, как было показано, обеспечивает самую современную производительность для большого количества табличных наборов данных. В двух словах, CatBoost выполняет повышение градиента на забытых (просмотренных) деревьях решений (таблицах решений) (Кохави, 1994; Лу и Обухов, 2017), что делает вывод очень эффективным, а метод довольно устойчив к переобучению. По своей сути, предлагаемая архитектура NODE обобщает CatBoost, делая выбор функции разделения и маршрутизацию дерева решений дифференцируемыми. В результате архитектура NODE полностью дифференцируема и может быть включена в любой вычислительный граф существующих пакетов DL, таких как TensorFlow или PyTorch. Кроме того, NODE позволяет создавать многоуровневые архитектуры, которые напоминают вариант «глубокого» GBDT, который обучается от начала до конца, что никогда ранее не предлагалось. Помимо использования таблиц решений, не обращающих внимания, другим важным выбором дизайна является недавнее преобразование entmax (Петерс и др., 2019), которое эффективно выполняет «гибкий» выбор разделяющей функции в деревьях решений внутри архитектуры NODE. Как обсуждается в следующих разделах, эти варианты дизайна имеют решающее значение для достижения самых современных характеристик. В большом количестве экспериментов мы сравниваем предложенный подход с ведущими реализациями GBDT с идентифицированными гипер-параметрами и демонстрируем, что NODE последовательно превосходит конкурентов по большинству наборов данных.

В целом, основные выводы нашей работы можно резюмировать следующим образом:

1. Мы представляем новую архитектуру DNN для машинного обучения табличным данным. Насколько нам известно, наш метод является первым успешным примером архитектуры глубокого обучения, который существенно превосходит ведущие пакеты GBDT по табличным данным.

2. С помощью обширной экспериментальной оценки на большом количестве наборов данных мы показываем, что предлагаемая архитектура NODE превосходит существующие реализации GBDT.

3. Реализация NODE PyTorch доступна онлайн.

Остальная часть статьи организована следующим образом. В разделе 2 мы рассмотрим предыдущую работу, относящуюся к нашему методу. Предлагаемая архитектура ансамблей нейронных решений, не обращающих внимания, описана в разделе 3 и экспериментально оценена в разделе 4. Раздел 5 завершает статью.

2. Литературный обзор и постановка задачи

В этом разделе мы кратко рассмотрим основные идеи из предыдущих работ, которые имеют отношение к нашему методу.

Современное состояние табличных данных. Ансамбли деревьев решений, такие как GBDT (Фридман, 2001) или случайные леса (Барандиаран, 1998), в настоящее время являются лучшим выбором для задач с табличными данными. В настоящее время существует несколько ведущих пакетов GBDT, таких как XGBoost (Chen & Гестрин, 2016), LightGBM (Ке и др., 2017), CatBoost (Прохоренкова и др., 2018), которые широко используются как академиками, так и практиками ML. Хотя эти реализации различаются в деталях, по большинству задач их производительность не сильно отличается (Прохоренкова и др., 2018; Ангель и др.). Наиболее важным отличием CatBoost является то, что он использует деревья решений без памяти (ODT) в качестве слабого обучения. Поскольку ODT также являются важным компонентом нашей архитектуры NODE, мы обсудим их ниже.

Деревья решений без памяти («Забывчивые деревья решений»). «Забывчивое дерево решений» - это обычное дерево глубины d, которое ограничено использованием одной и той же разделительной функции и порога разграничения (отделения) во всех внутренних узлах одинаковой глубины. Это ограничение, по сути, позволяет представлять ODT в виде таблицы с 2d-записями, соответствующими всем возможным комбинациям d-разбиений (Lou & Obukhov, 2017). Конечно, из-за вышеуказанных ограничений ODT значительно хуже обучаются по сравнению с неограниченными деревьями решений. Однако в ансамбле решений такие деревья менее склонны к переобучению, что, как было показано, хорошо сочетается с методом роста градиента (Прохоренкова и др., 2018). Кроме того, вывод в ODTS очень эффективен: можно параллельно вычислять d независимых двоичных разбиений и возвращать соответствующую запись таблицы. В отличие от этого, деревья решений с памятью требуют последовательной оценки d-разбиений

Дифференцируемые деревья. Существенным недостатком древовидных подходов является то, что они обычно не допускают сквозной оптимизации и используют «жадные алгоритмы» (процедуры) локальной оптимизации для построения дерева. Таким образом, они не могут быть использованы в качестве компонента для конвейерного подхода, обучения сквозным способом. Чтобы решить эту проблему, в нескольких работах (Концхидер и др., 2015; Янг и др., 2018; Лэй и др., 2018) предлагается «смягчить» функции принятия решений во внутренних узлах дерева, чтобы построить общую (интегральную) функцию дерева и маршрутизацию дерева дифференцированно. В нашей работе мы выступаем за использование недавнего преобразования entmax (Петерс и др., 2019) для ”смягчения” деревьев решений. Мы подтверждаем его преимущества перед ранее предложенными подходами в экспериментальном разделе.

Преобразование Entmax (Энтмакс). Ключевым строительным блоком нашей модели является преобразование entmax (Петерс и др., 2019), которое сопоставляет вектор вещественных оценок с дискретным распределением вероятностей. Это преобразование обобщает традиционный softmax и его альтернативу sparsemax, обеспечивающую разреженность (Martins & Astudillo, 2016), которая уже привлекла значительное внимание в широком спектре приложений: вероятностный вывод, ситуационное моделирование, нейронное внимание (Niculae & Blondel, 2017; Niculae и др., 2018; Лин и др., 2019). Entmax способен создавать разреженные распределения вероятностей, где большинство вероятностей точно равно нулю. В этой работе мы утверждаем, что entmax также является подходящим индуктивным смещением в нашей модели, которое позволяет строить дифференцируемое раздельное решение во внутренних узлах дерева. Интуитивно entmax может изучать решения о разделении на основе небольшого подмножества объектов данных (до одного, как в классических деревьях решений), избегая нежелательного влияния со стороны других. В качестве дополнительного преимущества использование entmax для выбора объектов позволяет выполнять эффективный с вычислительной точки зрения вывод с использованием разреженных предварительно вычисленных векторов выбора, как описано ниже в разделе 3.

Многослойные недифференцируемые архитектуры. Другое направление работы (Miller et al., 2017; Zhou & Feng, 2017; Feng et al., 2018) способствует созданию многослойных архитектур из недифференцируемых блоков, таких как случайные леса или ансамбли GBDT. Например, (Zhou & Feng, 2017; Miller et al., 2017) предлагают использовать укладку нескольких «случайных лесов», которые обучаются отдельно. В недавней работе (Feng et al., 2018) представлены многослойные GBDT и предложена процедура обучения, которая не требует, чтобы каждый компонент слоя был дифференцируемым. Хотя в этих работах сообщается о незначительных улучшениях по сравнению с частными аналогами, им не хватает возможностей для сквозного обучения, что может привести к снижению производительности. Напротив, мы утверждаем, что сквозное обучение имеет решающее значение, и подтверждаем это утверждение в экспериментальном разделе.

Конкретный DNN для табличных данных. В то время как в ряде предыдущих работ предлагались архитектуры, предназначенные для табличных данных (Ke et al., 2018; Shavitt & Segal, 2018), они в основном не сравниваются с правильно настроенными реализациями GBDT, которые являются наиболее подходящими базовыми показателями. В недавнем препринте (Ke et al., 2018) сообщается о незначительном улучшении по сравнению с GBDT с параметрами по умолчанию, но в наших экспериментах базовая производительность намного выше. Насколько нам известно, наш подход является первым, который последовательно превосходит настроенные GBDTS по большому количеству наборов данных.

3. Нейронные ансамбли забывчивых деревьев

Мы представляем архитектуру Neural Oblivious Decision Ensemble (NODE) с послойной структурой, аналогичной существующим моделям глубокого обучения. В двух словах, наша архитектура состоит из дифференцируемых деревьев решений с забыванием (ODT), которые обучаются сквозному обратному распространению. Мы описываем нашу реализацию уровня дифференцируемых NODE в разделе 3.1, полную архитектуру модели в разделе 3.2, а процедуры обучения и вывода - в разделе 3.3.

3.1. Дифференцируемые забывчивые деревья решений.

Основным строительным блоком нашей модели является уровень нейронного ансамбля принятия решений (NODE). Слой состоит из m дифференцируемых деревьев решений с забвением (ODT) равной глубины d. В качестве входных данных все m деревьев получают общий вектор x ∈ R_n, содержащий n числовых объектов. Ниже мы опишем конструкцию единственного дифференцируемого ODT.

По своей сути ODT - это таблица решений, которая разбивает данные по разделяющим функциям и сравнивает каждую функцию с изученным порогом. Затем дерево возвращает один из двух возможных ответов, соответствующих результату сравнения. Следовательно, каждый ODT полностью определяется его функциями расщепления

f ∈ R^d, порогами расщепления b ∈ R^d и d-мерным тензором ответов R ∈ R ^{{2 × 2 × 2}d} . В этой записи выходные данные дерева определяются как:

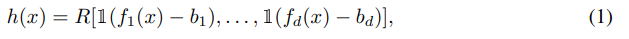
где 1(·) обозначает функцию Хевисайда.

Чтобы сделать вывод по дереву (1) дифференцируемым, мы заменим выбор функции разделения f_i и оператор сравнения 1(f_i(x) − b_i) их непрерывными аналогами. Существует несколько существующих подходов, которые можно использовать для моделирования дифференцируемых функций выбора в деревьях решений (Янг и др., 2018), например, reinforce (Уильямс, 1992) или Gumbel-softmax (Янг и др., 2016). Однако эти подходы обычно требуют длительного времени обучения, что может иметь решающее значение на практике.

Вместо этого мы предлагаем использовать преобразование α-entmax (Петерс и др., 2019), поскольку оно способно изучать разреженные варианты, зависящие только от нескольких функций, с помощью стандартного градиентного спуска. Следовательно, функция выбора заменяется взвешенной суммой признаков с весами, вычисляемыми как entmax по обучаемой матрице выбора признаков F ∈ R^d×n:

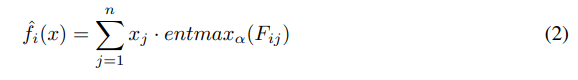
Аналогично, мы ослабляем функцию Хевисайда 1 (f_i (x)−b_i) как энтмакс двух классов, который мы обозначаем как σ_α(x) = entmax_a([x, 0]). Поскольку разные объекты могут иметь разные характерные масштабы, мы используем масштабированную версию

c_i (x) = σ_α ( (f_i(x)−b_i) / t_i) соответственно

где b_i и t_i являются обучаемыми параметрами для пороговых значений и . На основе значений c_i (x), мы определяем тензор ”выбора” C ∈ R^{{2 × 2 × 2}d} тензор R путем вычисления внешнего произведения всех c_i:

Затем окончательное предсказание вычисляется как взвешенная линейная комбинация записей тензора отклика R с весами из записей тензора выбора C:

Обратите внимание, что такое ослабление равно классическому недифференцируемому ODT h (x) (1), если f как функция выбора объектов, так и пороговые функции достигают однократного состояния, т.е. entmax всегда возвращает ненулевые веса для одного объекта, а c_i всегда возвращает лишь нули или единицы. Наконец, выходные данные NODE уровня составляются как объединение выходных данных m отдельных деревьев [ˆh₁(x),..., ˆh_m(x)].

Многомерные древовидные выходные данные. В приведенном выше описании мы предположили, что выходные данные дерева являются одномерными ˆh(x) ∈ R. Для задач классификации, где NODE предсказывает вероятности каждого класса, мы используем многомерные выходные данные дерева ˆh(x) ∈ R^|C|, где |C| - количество классов. Уровень NODE, описанный выше, может обучаться отдельно или в рамках сложной структуры, например, полностью связанных слоев, которые могут быть организованы в многоуровневые архитектуры. В этой работе мы представляем новую архитектуру, следуя популярной модели DenseNet (Хуан и др., 2017), и обучаем ее сквозному использованию с помощью обратного распространения.

3.2. Углубляясь в архитектуру NODE

Уровень NODE, описанный выше, может обучаться отдельно или в рамках сложной структуры, например, полностью связанных слоев, которые могут быть организованы в многоуровневые архитектуры. В этой работе мы представляем новую архитектуру, следуя популярной модели DenseNet (Хуан и др., 2017), и обучаем ее сквозному использованию с помощью обратного распространения.

Подобно DenseNet, наша архитектура представляет собой последовательность из k узловых уровней (см. Раздел 3.1), где каждый уровень использует объединение всех предыдущих уровней в качестве входных данных. Входной уровень (нулевой) этой архитектуры соответствует входным функциям x, доступным для всех последующих уровней. Благодаря такому дизайну наша архитектура способна изучать как неглубокие, так и глубокие правила принятия решений. Одно дерево на i-м уровне может полагаться на цепочки выходных данных уровня до i − 1 в качестве объектов, что позволяет ему фиксировать сложные зависимости. Результирующий прогноз представляет собой простое среднее значение всех деревьев решений из всех слоев.

Обратите внимание, что в многоуровневой архитектуре, описанной выше, выходные данные дерева ˆh(x) из ранних слоев используются в качестве входных данных для последующих слоев. Следовательно, мы не ограничиваем размерность ˆh (x), которая равна числу классов и позволяем ей иметь произвольную размерность l, которая соответствует (d + 1)-мерному тензору отклика R ∈ R ^{{2 ×2 × 2) }d × l}. При усреднении прогнозных результатов по всем слоям для задач классификации используются только первые |C| координаты ˆh(x), а для задач регрессии – лишь первые. В целом, l является дополнительным гипер-параметром с типичными значениями в [1,3].

3.3. Обучение

Здесь мы кратко излагаем детали нашего протокола обучения.

Предварительная обработка данных. Сначала мы преобразуем каждый объект данных в соответствии с нормальным распределением с помощью квантильного преобразования. В экспериментах мы заметили, что этот шаг был важен для стабильного обучения и более быстрой конвергенции.

Инициализация. Перед обучением мы выполняем инициализацию с учетом данных (Мишкин и Матас, 2016), чтобы получить хорошие начальные значения параметров. В частности, мы инициализируем матрицу выбора признаков равномерно F_ij ∼ U(0,1), в то время как пороговые значения b инициализируются случайными значениями признаков f_i(x), наблюдаемыми в первом пакете данных. Шкалы ti инициализируются таким образом, что все образцы в первой партии принадлежат линейной области σα и, следовательно, получают ненулевые градиенты. Наконец, записи тензора отклика инициализируются стандартным нормальным распределением R[i₁,...,i_d] ∼ N(0,1).

Обучение. Что касается существующих архитектур DNN, то NODE обучается от начала до конца с помощью мини-пакетного SGD. Мы совместно оптимизируем все параметры модели: F,b,R. В этой работе мы экспериментировали с традиционными целевыми функциями (кросс-энтропия для классификации и среднеквадратичная ошибка для регрессии), но также можно использовать любую дифференцируемую цель. В качестве метода оптимизации мы используем недавний квазигиперболический импульс и Adam (QHAdam) с параметрами, рекомендованными в оригинальной статье (Ma & Yarats, 2018). Мы также усредняем параметры модели по c = 5 последовательным контрольным точкам (Измайлов и др., 2018) и выбираем оптимальную точку остановки в наборе данных проверки задержки.

Вывод. Во время обучения значительная часть времени тратится на вычисление функции entmax и умножение тензора выбора. Как только модель обучена, можно предварительно вычислить селекторы (разделители) объектов entmax и сохранить их в виде разреженного вектора (например, в формате координат (coo)), что делает вывод более эффективным.

4. Эксперименты

В этом разделе мы сообщаем о результатах сравнения нашего подхода с ведущими пакетами GBDT. Мы также предоставляем несколько исследований абляции, которые демонстрируют влияние каждого выбора дизайна в предлагаемой архитектуре NODE.

4.1. Сравнение с современными техниками реализаций

В качестве наших основных экспериментов мы сравниваем предлагаемую архитектуру NODE с двумя современными реализациями GBDT на большом количестве наборов данных. Во всех экспериментах мы устанавливаем параметр α в преобразовании entmax равным 1,5. Все остальные детали протокола сравнения описаны ниже.

Наборы данных. Мы проводим большинство экспериментов с шестью табличными наборами данных с открытым исходным кодом из разных доменов: Epsilon, YearPrediction, Higgs, Microsoft, Yahoo, Click. Подробное описание наборов данных доступно в приложении. Все наборы данных предоставляют разбиения на обучение/тестирование, и мы использовали 20% выборок из набора обучения в качестве набора проверки для настройки гипер-параметров. Для каждого набора данных мы фиксируем разделение train/val/test для справедливого сравнения. Для наборов данных классификации (Эпсилон, Хиггс, Клик) мы минимизируем потери перекрестной энтропии и сообщаем об ошибке классификации. Для наборов данных регрессии и ранжирования (YearPrediction, Microsoft, Yahoo) мы минимизируем и сообщаем о среднеквадратичной ошибке (что соответствует точечному подходу к обучению ранжированию).

Методы. Мы сравниваем предлагаемую архитектуру NODE со следующими базовыми показателями:

• Catboost – недавняя реализация GBDT (Прохоренкова и др., 2018), в которой используются забытые деревья решений в качестве слабых учеников, мы используем реализацию с открытым исходным кодом, предоставленную авторами;

• XGBoost – самая популярная реализация GBDT, широко используемая в соревнованиях по машинному обучению (Chen & Гестрин, 2016), мы используем реализацию с открытым исходным кодом, предоставленную авторами;

• FCNN – глубокая нейронная сеть, состоящая из нескольких полностью связанных слоев со слоями нелинейности ReLU (Nair & Hinton, 2010).

Режимы. Мы проводим сравнение в двух нижеследующих режимах, которые являются наиболее важными на практике.

1. Гипер-параметры по умолчанию. В этом режиме мы сравниваем методы как простые в настройке наборы инструментов, которые могут быть использованы непрофессиональной аудиторией. А именно, здесь мы не настраиваем гипер-параметры и используем параметры по умолчанию, предоставляемые пакетами GBDT. Единственным настраиваемым параметром здесь является количество деревьев (до 2048) в CatBoost/XGBoost, которое устанавливается на основе набора проверки. Мы не сравниваем с FCNN в этом режиме, так как он обычно требует большой настройки, и мы не нашли набор параметров, подходящих для всех наборов данных. Архитектура по умолчанию в нашей модели содержит только один слой с 2048 деревьями решений шестой глубины. Оба этих гипер-параметра были унаследованы из настроек пакета CatBoost для забытых деревьев решений. С этими параметрами архитектура NODE является неглубокой, но она по-прежнему выигрывает от сквозного обучения с помощью обратного распространения.

2. Настроенные гипер-параметры. В этом режиме мы настраиваем гипер-параметры как для NODE, так и для конкурентов в подмножествах проверки. Оптимальная конфигурация для NODE содержит от двух до восьми уровней NODE, в то время как общее количество деревьев во всех слоях не превышает 2048. Подробная информация об оптимизации гипер-параметров приведена в приложении.

Результаты сравнения обобщены в таблицах 1 и 2. Для всех методов мы сообщаем о средней производительности и стандартных отклонениях, вычисленных за десять запусков с различными случайными начальными значениями. Ниже приводятся несколько ключевых замечаний.

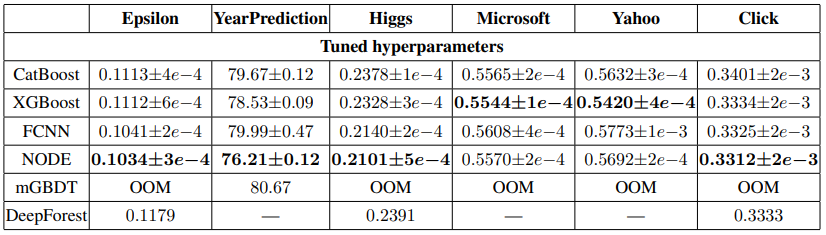
1. С гипер-параметрами по умолчанию предлагаемая архитектура NODE последовательно превосходит как CatBoost, так и XGBoost во всех наборах данных. Полученные результаты свидетельствуют об использовании NODE в качестве удобного инструмента для машинного обучения табличным задачам.

2. Благодаря настроенным гипер-параметрам NODE также превосходит конкурентов по большинству задач. Двумя исключениями являются наборы данных Yahoo и Microsoft, где настроенный XGBoost обеспечивает высочайшую производительность. Учитывая большое преимущество XGBoost перед CatBoost на Yahoo, мы предполагаем, что использование деревьев решений, не обращающих внимания, является неуместным индуктивным смещением для этого набора данных. Это подразумевает, что NODE должен быть расширен до не забывающих деревьев, которые мы оставляем для будущей работы.

3. В режиме с подобранными (идентифицированными) гипер-параметрами на некоторых наборах данных FCNN превосходит GBDT, в то время как на других GBDT превосходит. Между тем, предлагаемая архитектура NODE представляется универсальным инструментом, обеспечивающим высочайшую производительность при выполнении большинства задач.

Для полноты картины мы также стремились сравнить с ранее предложенными архитектурами для глубокого обучения табличным данным. К сожалению, многие работы не публиковали исходный код. Мы смогли провести только частичное сравнение с mGBDT (Feng et al., 2018) и DeepForest (Zhou & Feng, 2017), исходные коды которых доступен. Для обеих базовых линий мы используем реализации, предоставленные авторами, и настраиваем параметры в наборе проверки. Обратите внимание, что реализация DeepForest доступна только для задач классификации. Более того, обе реализации плохо масштабируются, и для многих наборов данных мы получили ошибку нехватки памяти (ООМ). На наборах данных в наших экспериментах оказывается, что правильно настроенные GBDTS превосходят как (Feng et al., 2018), так и (Zhou & Feng, 2017).

4.2. Абляционный анализ

В этом разделе мы анализируем ключевые компоненты архитектуры, которые определяют нашу модель.

Функции выбора. Для построения дифференцируемых деревьев решений требуется функция, которая выбирает элементы из набора. Такая функция необходима как для выбора объектов разделения, так и для маршрутизации дерева решений. Мы провели эксперимент с четырьмя возможными вариантами, каждый из которых имел разные последствия:

• Softmax изучает плотные правила принятия решений, в которых все элементы имеют ненулевые веса;

• Gumbel-Softmax (Jang и др., 2016) учится стохастически выбирать один элемент из набора;

• Sparsemax (Martins & Astudillo, 2016) изучает разреженные правила принятия решений, в которых только несколько элементов имеют ненулевые веса;

• Entmax (Петерс и др., 2019) обобщает как sparsemax, так и softmax, он способен изучать разреженные правила принятия решений, но более гибко, чем sparsemax, более подходящий для оптимизации на основе градиентов (для сравнения параметр α был установлен равным 1.5).

Мы экспериментально сравниваем четыре вышеприведенных варианта, как с неглубокими, так и с глубокой архитектурой в таблице 3. Мы используем одну и ту же функцию выбора, как для выбора объектов, так и для маршрутизации по дереву во всех экспериментах. В Gumbel-Softmax мы заменили его жестким argmax one-hot во время вывода. Результаты ясно показывают, что Entmax с α = 1,5 превосходит конкурентов во всех экспериментах. Во-первых, таблица 3 демонстрирует, что sparsemax и softmax не являются универсальными функциями выбора. Например, в наборе данных YearPrediction sparsemax превосходит softmax, в то время как в наборе данных Epsilon softmax превосходит его. В свою очередь, entmax обеспечивает отличную эмпирическую производительность во всех наборах данных. Другое наблюдение заключается в том, что Gumbel-Softmax неспособен изучать глубокие архитектуры, как с постоянными, так и с отожженными температурными режимами. Такое поведение, вероятно, вызвано стохастичностью Gumbel-Softmax, а отклики на первых слоях слишком зашумлены, чтобы позволять выбирать релевантно полезные функции для последних слоев.

Важность функции. В этой серии экспериментов мы анализируем внутренние представления, усвоенные архитектурой NODE. Мы начнем с оценки значимости объектов из разных слоев многослойного ансамбля с помощью перестановки важности объектов, первоначально введенной в (Breiman, 2001). А именно, для 10 000 объектов из набора данных Хиггса мы случайным образом смешиваем значения каждого объекта (исходного или изученного на каком-либо узловом уровне) и вычисляем отклонение ошибки классификации. Затем для каждого слоя мы разделяем значения важности объектов на семь равных ячеек и вычисляем общую важность объектов для каждой ячейки, как показано на рисунке 3 (слева вверху). Мы обнаружили, что чаще используются объекты первого слоя, при этом важность объектов уменьшается с глубиной анализа. На этом рисунке показано, что глубокие слои способны создавать важные функции, хотя более ранние слои имеют преимущество из-за архитектуры DenseNet. Затем мы оценили средний абсолютный вклад отдельных деревьев в окончательный результат, представленный на рисунке 3 (слева внизу). Можно увидеть обратную тенденцию: глубокие деревья, как правило, вносят больший вклад в окончательный ответ. На рисунке 3 (справа) четко показано, что в окончательном ответе (результате) наблюдается корреляция значимости и вклада функций, что подразумевает, что основная роль более ранних слоев заключается в создании информативных функций, в то время как последние слои в основном используют их для точного прогнозирования.

Время выполнения обучения/вывода. Наконец, мы сравниваем время выполнения NODE с временными характеристиками современных реализаций GBDT. В таблице 4 мы сообщаем о времени обучения и вывода для миллионов объектов из набора данных YearPrediction. В этом эксперименте мы оцениваем ансамбли из 1024 деревьев глубиной шесть со всеми остальными параметрами, значения которых установлены по умолчанию. Наша установка GPU имеет один графический процессор 1080Ti и 2 ядра процессора. В свою очередь, наша установка процессора оснащена 28-ядерным процессором Xeon E5-2660 v4 (который стоит почти вдвое дороже графического процессора). Мы используем CatBoost v0.15 и XGBoost v0.90 в качестве базовых, в то время как вывод NODE выполняется на PyTorch v 1.1.0. В целом, время вывода узлов соответствует сильно оптимизированным библиотекам GBDT, несмотря на то, что они реализованы в PyTorch (без пользовательских ядер).

5. Заключение

В этой статье мы представляем новую архитектуру DNN для глубокого обучения разнородным табличным данным. Архитектура представляет собой дифференцируемые глубокие GBDT, обучаемые от начала до конца с помощью обратного распространения. В ходе обширных экспериментов мы демонстрируем преимущества нашей архитектуры перед существующими конкурентами с помощью стандартных и настроенных гипер-параметров. Перспективным направлением исследований является включение узлового уровня в сложные конвейерные вычисления и обучение с помощью обратного распространения. Например, в мультимодальных задачах уровень NODE может использоваться как способ включения табличных данных, поскольку CNN в настоящее время используются для изображений, или RNN используются для последовательностей.

ПРИЛОЖЕНИЕ A

A.1. Описание наборов данных

В наших экспериментах мы использовали шесть табличных наборов данных, описанный в Эпсилоне Таблицы 5:

1)   Высоко размерный набор данных от ПАСКАЛЯ, проблема - набор из двух предметов и их классификация;

2)   YearPrediction - подмножество MSD Challenge (крупная открытая оценка музыкальных рекомендаций в офлайн-режиме), и задача состоит в том, чтобы предсказать год выпуска песни при помощи аудио особенностей;

3)   Хиггс - набор данных из хранилища UCI ML, проблема состоит в том, чтобы предсказать, производит ли данное событие бозоны Хиггса или нет;

4)   Microsoft - Обучение и анализ набора данных, используется 136-мерных векторов особенности, извлеченных от пар URL вопроса, у каждой пары есть своя ценность от 0 (не важный) 4 (совершенно релевантный);

5)   Yahoo – очень похожий набор данных рейтинга с парами URL вопроса, маркированными от 0 до 4, мы рассматриваем место проблемы как регресс (который соответствует подходу pointwise);

6)   Click (Щелчок) – подмножество из данных из Кубка KDD 2012 года, для строительства подмножества, мы выбираем случайным образом типовые 500 000 объектов из положительного класса и 500 000 объектов отрицательного класса.

Категориальные особенности были преобразованы к числовым через кодирующее устройство Leave-One-Out («Пропуск по одному») от пакета кодирующих устройств категории Scikit-learn (широко используемый пакет Python для Data Science и Machine Learning).

A.2. Оптимизация Гипер-параметров

Чтобы настроить гипер-параметры, мы выполнили случайное стратифицированное разделение полных данных тренировки (80%) и проверки обучения устанавливают (20%) для Эпсилона, YearPrediction, Хиггса, Microsoft и Click наборы данных. Для Yahoo мы используем разделение train/val/test, обеспеченное авторами набора данных. Мы используем библиотеку Hyperopt3, чтобы оптимизировать Catboost, XGBoost и гипер-параметры FCNN. Для каждого метода мы выступаем 50 шагов алгоритма оптимизации Tree-structured Parzen Estimator (TPE). Как заключительная конфигурация, мы выбираем набор гипер-параметров, соответствуя самой маленькой потере на наборе проверки.

A.2.1. CATBOOST И XGBOOST

На каждом повторении, номер деревьев был определен на основе набора проверки с максимальным деревом в 2048. Ниже список гипер-параметров и их мест поиска для Catboost.

• темп обучения: однородная регистрация распределение;

• случайная сила: дискретное однородное распределение;

• максимальный размер: дискретное однородное распределение;

• лист l2 reg: однородная регистрация распределения;

• упаковка по температуре: однородное распределение;

• итерации оценок листьев: дискретное однородное распределение;

XGBoost настроил параметры и их места поиска:

• eta: однородная регистрация распределения;

• максимальная глубина: дискретное однородное распределение;

• подобразец: однородное распределение;

• двоичное дерево: однородное распределение;

• двухуровневый colsample: однородное распределение;

• минимальный детский вес: однородное распределение;

• альфа: однородный выбор;

• лямбда: однородный выбор;

• гамма: однородный выбор.

A.2.2. FCNN

Полностью связанные нейронные сети были настроены, используя библиотеку Hyperas 10, которая является оболочкой Keras для Гипервыбора. Мы считаем FCNN построенной из следующих блоков: Dense-ReLU-Dropout. Количество единиц в каждом слое независимо друг от друга, и стоимость (вес) удаленной ветви - то же для целой сети. Сети обучены с оптимизатором Адама с усреднением образцовых параметров по c=5 последовательным контрольно-пропускным пунктам (Измайлов и др., 2018) и рано останавливающийся на проверке. Пакетный размер прикреплен к 1 024 для всех наборов данных.
Ниже список настроенных гипер-параметров:

• количество слоев: дискретное однородное распределение;

• количество единиц: равномерное дискретное распределение по набору;

• темп обучения: однородное распределение;

• удаление (выбраковка): однородное распределение.

А.2.3 NODE

Ансамбли Neural Oblivious Decision Ensembles были настроены с помощью поиска по сетке по следующим значениям гиперпараметров. В многоуровневом NODE мы используем одинаковую архитектуру для всех слоев, т. е. одинаковое количество деревьев одинаковой глубины. Общее количество деревьев здесь обозначает общее количество деревьев на всех слоях. Для каждого набора данных мы используем максимальный размер пакета, который помещается в память графического процессора. Мы всегда используем скорость обучения 10⁻³.