Simple Modifications to Improve Tabular Neural Networks

 Аннотация

Растет интерес к архитектуре нейронных сетей для табличных данных. В последнее время появилось множество табличных моделей глубокого обучения общего назначения, вычислительная мощность которых иногда соперничает с возможностями деревьев решений с градиентным бустингом (усилением) (GBDT). Последние модели черпают вдохновение из различных источников, включая GBDT (gradient boosted decision trees), машины факторизации и нейронные сети из других областей применения. Предыдущие табличные нейронные сети также используются, но, возможно, недостаточно учтены, особенно для моделей, связанных с конкретными табличными задачами. В данной статье основное внимание уделяется нескольким таким моделям и предлагаются модификации для повышения их производительности. Показано, что при модификации эти модели конкурируют с ведущими табличными моделями общего назначения, включая GBDT.

 1. Введение

В последнее время многие архитектуры нейронных сетей были представлены в качестве табличных решений общего назначения. Некоторые примеры: Tabnet (Арик и Пфистер 2020), TabTransformer (Хуан и др. 2020), NODE (Попов, Морозов и Бабенко 2019), DNF-сеть (Абутбул и др. 2020). Внедрение этих и других моделей демонстрирует растущий интерес к применению глубокого обучения к табличным данным. Это не связано с отсутствием решений, выходящих за пределы возможностей глубокого обучения. Деревья решений с градиентным бустингом (GBDT) являются классом очень хороших моделей общего назначения и фактически часто используются табличными моделями глубокого обучения – как в качестве источника вдохновения, так и в качестве стандарта по производительности.

Большой интерес к табличным моделям глубокого обучения обусловлен преимуществами, которые они уже имеют по сравнению с GBDT или другими устоявшимися моделями. Возможно, самым большим преимуществом является то, что нейронные сети обладают потенциалом для сквозного обучения (end-to-end learning), устраняя необходимость в управляемом категориями (категориально) ручном кодировании или другой разработке функций. Модели NN (neural network) также предоставляют больше возможностей для обучения, чем GBDT-модели. Например, они позволяют проводить непрерывное обучение потоковым данным (потоковому программированию) и, в более общем плане, позволяют корректировать изученные параметры NN путем обучения новым данным. Модели нейронных сетей также лучше подходят для неконтролируемого предварительного обучения; например, см. (Арик и Пфистер 2020) и (Хуанг и др. 2020).

Еще до недавнего появления табличных моделей общего назначения нейронные сети доказали свою эффективность в конкретных проблемах с использованием табличных данных, в частности, с использованием показателей кликов (CTR) и систем рекомендаций. Многие модели нейронных сетей использовали эти два приложения в качестве основной мотивации, в том числе Wide & Deep (Ченг и др., 2016), Deep & Cross (Ван и др., 2017), Продуктовые нейронные сети (PNN) (Цюй и др., 2016), xDeepFM (Лиан и др., 2018), aUtoiNT (Сонг и др., 2019) и FiBiNet (Хуан, Чжан и Чжан 2019). Методы этих моделей структурно применимы к задачам с табличными данными в более общем плане. Однако, за исключением AutoInt, эти модели обычно не фигурировали в сравнениях производительности ранее использованных общих табличных моделей.

Разумно предположить, что модели, созданные специально под решения общего назначения, будут превосходить любую из специфичных моделей при оценке в различных табличных наборах данных. Некоторые свидетельства подтверждают это предположение. Например, (Горишний и др., 2021) сравнивает Autoint и более новую общую табличную модель, причем Autoint работает менее хорошо. С другой стороны, бывают также случаи, когда модели, созданные для определенной цели, превосходят более новые табличные модели общего назначения. В той же статье также показано, что ResNet (He et al. 2015), предназначенный для классификации изображений, может превосходить некоторые модели общего назначения. Следовательно, существующие табличные нейронные сети, связанные с конкретными табличными задачами, возможно, стоит рассматривать и при поиске более общих решений.

Глядя в другом направлении для вдохновения, многослойные персептроны (MLP; см. Рис. 1a), пожалуй, являются самыми простыми и наиболее универсальными NN. Базовые и модифицированные версии часто включаются в сравнение моделей, иногда демонстрируя удивительно хорошие результаты (см. Результаты в разделе 3.4 и соответствующую работу в разделе 6). Когда они работают хорошо, их простота делает их привлекательным вариантом. Их простота делает их также привлекательным вариантом для реализации и тестирования новых идей и интерпретации их эффекта.

С учетом этого контекста в настоящей статье рассматриваются модели MLP, PNN и AutoInt, предлагается несколько простых модификаций, чтобы сделать их конкурентоспособными с недавними табличными NN общего назначения. Приведенные ниже результаты показывают, что эта цель достигнута. Фактически, модифицированные модели, по-видимому, превосходят недавно предложенные модели и, возможно, даже превосходят GBDT от LightGBM (Ke et al. 2017) в наборах данных, используемых в (Huang et al. 2020).

Основные материалы этой статьи:

1. Несколько простых модификаций, которые позволяют моделям MLP, PNN и AUTOINT работать наравне или лучше, чем недавние табличные NN общего назначения и GBDT.

2. Сравнение моделей по широкому спектру наборов данных, показывающих эффективность предлагаемых модификаций.

3. Демонстрация того, как одна модификация, в частности, способствует интерпретируемости модели.

Предлагаемые модификации, вероятно, полезны в более общем плане, чем показано здесь, в том числе, возможно, для некоторых сравниваемых моделей. Одна из предлагаемых модификаций, модель Leaky Gates («Дырявые ворота»), возможно, является новой, хотя и простой конструкцией; см. Раздел 5. Другие модификации использовались в других местах, но не применялись в этой комбинации, а также для улучшения PNN, AutoInt или аналогичных моделей. Кроме того, насколько мне известно, это первый случай, когда модифицированные версии моделей, как PNN и AutoInt, оказались конкурентоспособными с новыми табличными NN общего назначения.

Как организован данный документ:

1)  в разделе 2 описываются предлагаемые изменения;

2)  в разделе 3 объясняются эксперименты и приводятся результаты, показывающие, что модифицированные модели конкурируют с любой из моделей сравнения и, возможно, превосходят их;

3)  в разделе 4 оцениваются преимущества модификаций путем сравнения нескольких скорректированных (абляционных) вариантов моделей;

4)  в разделе 5 показано, как одна из предложенных модификаций может помочь понять модель и интерпретировать результаты;

5)  в разделе 6 обсуждаются некоторые недавние связанные с этим работы и то, как эта работа может вдохновить на будущие исследования.

 2. Модели и модификации

Пакетная нормализация выборки (GBN - Ghost batch norm) будет использоваться во всех моделях вместо нормы совокупности. Эта идея взята из Tabnet (Арик и Пфистер 2020) и первоначально была предложена в (Хоффер, Хубара и Соудри 2018). GBN позволяет использовать совокупности больших размеров, но с параметрами нормы совокупности, рассчитанными для небольших выборок. Одной из главных причин использования GBN здесь является ускорение обучения, но (Хоффер, Хубара и Соудри 2018) также показали, что GBN улучшает обобщение при использовании больших размеров выборок.

Подмодель «Дырявые ворота» также будут использоваться во всех моделях. Она представляет собой комбинацию двух простых элементов, поэлементного линейного преобразования, за которым следует активация LeakyReLU. «Дырявые ворота», возможно, являются чем-то новым, но их простота может сделать это маловероятным. Кроме того, существуют более сложные конструкции с тем же базовым эффектом. Для более подробного обсуждения негерметичных ворот и их последствий см. Раздел 5.

 2.1. MLP

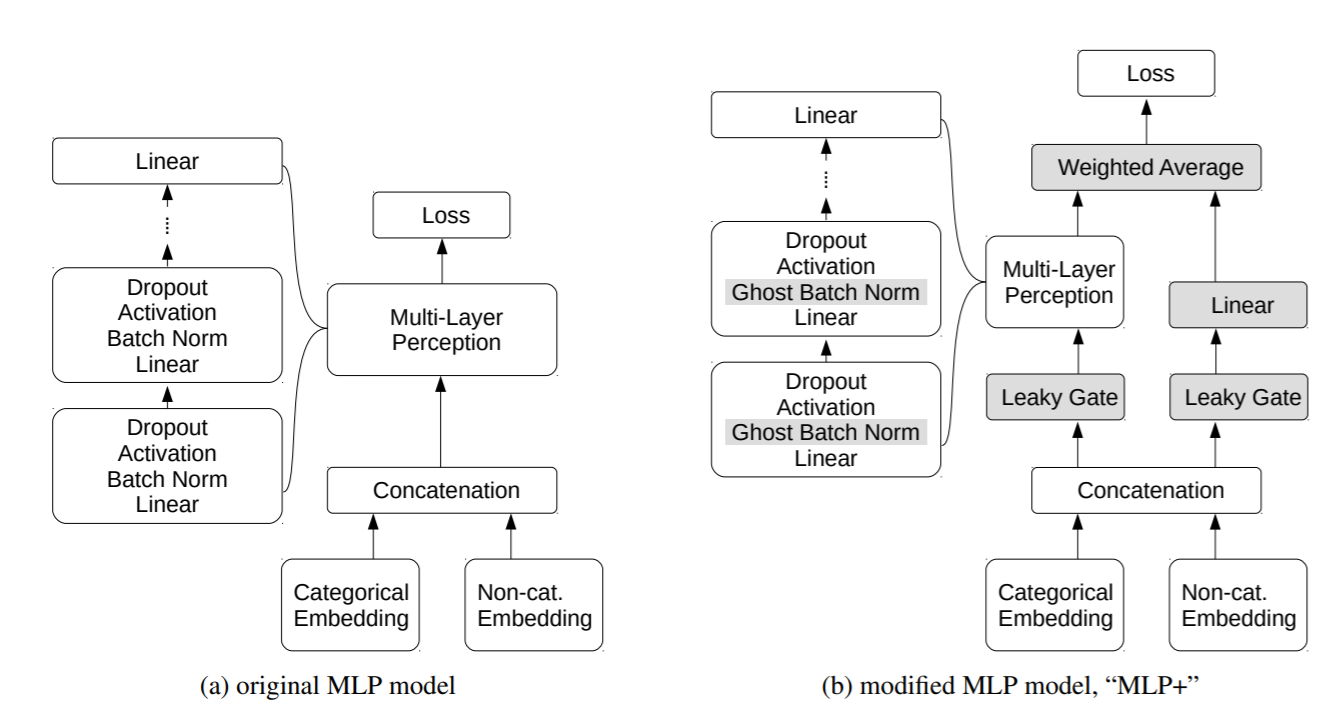
На рисунке 1a показана модель MLP (Multi-Layer Perceptron) до внесения изменений, а на рисунке 1b показана модель MLP после внесения изменений с серым цветом для измененных элементов.

Начиная с подблока «Многослойный персептрон», нормализация выборки заменяется Пакетной нормализацией выборки. Затем, согласно модели MLP AutoGluon (Erickson et al. 2020), справа от подблока MLP добавляется линейный слой (слой линейного преобразования). Слой пропуска - это всего лишь один полностью связанный линейный слой, который обеспечивает более короткий путь между внедрением и функцией потерь. В MLP AutoGluon выходные данные пропускного слоя суммируются с выходными данными подблока MLP. Здесь берется средневзвешенное значение, причем с весом, который идентифицирован или задан (например, экспертно). Наконец, пропускные вентили добавляются как перед подблоком MLP, так и перед линейным пропускным слоем.

Как показано в нижней части рисунка 1, встроены как категориальные, так и числовые входные данные. См. Раздел 2.5 для получения подробной информации о внедрениях.

Краткое описание изменений для создания MLP+:

1)    использовать пакетную нормализацию выборки вместо нормы партии;

2)    добавить линейный слой пропуска;

3)    использовать средневзвешенное значение выходных данных слоя пропуска и выходных данных основного слоя с изученным весом;

4)    добавить пропускной затвор как перед подблоком MLP, так и перед слоем пропуска.

Ссылки на несколько версий MLP будут даны позже. Чтобы уменьшить неопределенность, эта новая модифицированная версия будет называться «MLP+». Кроме того, «MLP+ блок» будет относиться к комбинации пропускных вентилей, подблока MLP, пропускного слоя и средневзвешенного значения.

 

2.2. PNN

Исходная модель PNN (Qu et al. 2016) имеет два основных компонента после встраивания, рис. 2a и 2b. Встроенные функции сначала проходят через внутренний или внешний блок продукта (или оба) для учета взаимодействия функций. Затем значения взаимодействия проходят через блок MLP.

На рисунке 2c компонент MLP модифицирован, как указано выше, чтобы стать блоком MLP+. Рядом с этими компонентами добавляется второй блок MLP+ для создания отдельного пути от встроенного ввода к выходу. Это похоже на пропуск слоя в модели MLP+, но здесь добавлена блокировка нескольких слоев вместо одного слоя. В модели «два столбца», подобной этой, два выходных данных обычно суммируются, но, как указано выше, используется средневзвешенное значение с изученным весом. Затем перед блоком продукта добавляется один пропускной вентиль (оба блока MLP+ также включают пропускные вентили), и снова встраиваются как категориальные, так и числовые входные данные.

В приведенном выше MLP+ некатегориальное встраивание структурно необязательно. В PNN и AutoInt это требуется, если всем функциям будет разрешено эквивалентное взаимодействие. PNN и AutoInt могут передавать не внедренные значения непосредственно в два блока MLP+, минуя блоки взаимодействия. Однако это позволило бы уменьшить количество взаимодействий между категориальными и некатегориальными значениями, что в целом представляется неоптимальным.

Наличие некатегориальных значений, обходящих блок взаимодействия, на самом деле распространено в табличных моделях с этой базовой структурой. Примером является модель TabTransformer (Хуан и др., 2020) в приведенных ниже сравнениях. Кроме того, в документе PNN (Qu и др., 2016) не упоминаются некатегориальные значения, поэтому они, скорее всего, либо не были разрешены, либо были разрешены, но обошли блок взаимодействия.

Краткое описание изменений в PNN:

1)    добавить пропускной затвор перед блоком преобразователем (продукта);

2)    изменить блок MLP на блок MLP+;

3)    добавить второй столбец MLP+;

4)    взять средневзвешенное значение двух выходов MLP+ с изученным весом.

 2.3. AutoInt

Вместо блока взаимодействия с продуктом в PNN Autoint используется блок взаимодействия с механизмом самоконтроля с несколькими головками (Song et al. 2019), согласно исследованиям (Vaswani et al. 2017). В остальном общая структура AutoInt и PNN аналогична. Следовательно, изменения в версии AutoInt с двумя столбцами почти такие же, как и в PNN, за исключением того, что a) у AutoInt уже был второй столбец MLP и b) AutoInt уже использовал встраивание для некатегориальных функций.

Краткое описание изменений в AutoInt:

1)    добавить Leaky Gate (скрытый вентиль) перед блоком самоконтроля;

2)    изменить блоки MLP на блоки MLP+;

3)    взять средневзвешенное значение двух выходов MLP+ вместо простой суммы.

 

2.4. Другие модели для рассмотрения

Существуют и другие табличные модели, которые имеют ту же базовую структуру, что и PNN или AutoInt, и, возможно, могли бы извлечь выгоду из этих модификаций. Например, структура TabTransformer аналогична PNN, а структура xDeepFM (Лиан и др., 2018) аналогична Autoint. Конечно, любая модель, включающая компонент MLP, потенциально может извлечь выгоду из изменений в MLP+.

2.5 Другие детали реализации.

В приведенных здесь реализациях используется LeakyReLU (Maas, Hannun и Ng 2013) в тех местах, где обычно используется ReLU. В частности, LeakyReLU - это активация, используемая в модели MLP+ и блоках MLP+ в PNN и Autoint.

Все модели используют одну и ту же схему встраивания. Каждому категориальному полю ввода f присваивается матрица вложения E_f размерности m × c_f, где m - размер вложения, а c_f - количество различных значений в поле. Если h – быстрое («горячее») встраивание значений поля, то для одного значения x_i встраивание e_i равно

Или, если значения полей закодированы как непрерывные целые числа 1, 2,...,c_f, то вложение для x_i является x-м столбцом i E_f. Элементы E_f изучаются вместе с другими параметрами модели.

Некатегориальные значения также будут внедрены с использованием метода, описанного в (Song et al. 2019). Каждому некатегориальному полю (параметру) f присваивается вектор-столбец V_f. Для одного значения x_i встраивание e_i равно

Другими словами, вектор встраивания каждого отдельного значения - это просто масштабирование вектора встраивания поля.

Модели PNN и AUTOINT требуют, чтобы размер вложения был одинаковым для всех столбцов (как категориальных, так и некатегориальных). В приведенных ниже экспериментах размер встраивания является параметром, подлежащим оптимизации. MLP+ не имеет такого же структурного требования к единому размеру встраивания и, как упоминалось выше, даже структурно не требует встраивания некатегориальных значений. Однако MLP + использует ту же схему встраивания в экспериментах ради единообразия и для уменьшения сложности логики поиска параметров.

Модели MLP+, PNN и Autoint реализованы в PyTorch (Paszke et al. 2019). Код доступен по адресу www.github.com/jrfiedler/xynn

 3. Эксперименты

 3.1. Данные

Результаты для этих моделей взяты из (Huang et al., 2020). Наборы данных такие же, как в документе TabTransformer (Хуан и др. 2020): 15 наборов данных из репозитория UCI, AutoML Challenge (Гайон и др. 2019) и Kaggle. Для всех наборов данных задача состоит в двоичной классификации. Размеры набора данных варьируются от 1 055 до 425 240 строк и от 10 до 308 входных объектов. Более подробная информация приведена в таблице 8 Приложения.

Для обучения (тестирования) модели, следует разбить свой набор данных на данные для обучения, проверки и задержки. Разделение набора данных - это 5-кратное разделение перекрестной проверки с 65% / 15% / 20% для обучения (проверки, задержки). Обучающий набор данных одинаков как для проверки, так и для конечных результатов тестирования. Набор несогласованных данных используется только для определения окончательной оценки модели. Для моделей, включенных в документ TabTransformer, 5-кратное разделение для каждого набора данных одинаково для всех моделей. Оценки для этих моделей скопированы здесь. Для типов моделей, представленных здесь, используется тот же подход, но исходное начальное значение неизвестно, поэтому используются два новых начальных значения. Таким образом, для MLP+, PNN и AutoInt для каждой сводки используется в общей сложности 10 подходящих моделей.

 3.2. Параметры модели

Статические параметры. Для каждого набора данных, размер пакета и размер пакетно нормализованной выборки являются статическими для всех моделей; см. Таблицу 8 приложения. Все модели используют снижение энтропии взаимодействий оптимизатора Adam (Kingma и Ba 2017) без снижения веса и планировщика PyTorch StepLR для снижения скорости обучения путем умножения на 0,95 с интервалом в выбранное количество периодов (итераций).

Поиск по параметрам. Параметры были настроены с использованием байесовской оптимизации гиперпараметров (HPO) с помощью пакета Optuna (Akiba et al. 2019). Двадцать раундов оптимизации были использованы для каждой модели при каждом разделении данных. Оптимальные параметры, включая количество периодов обучения, были определены путем максимизации меры валидации AUROC (площади под кривой ROC) согласно (Брэдли 1997) с ранним временем остановки 15 периодов (итераций). Моделям было разрешено использовать разные параметры для различных изменений (генераций) одного и того же набора данных. Полный список параметров поиска параметров см. в таблице 7 приложения.

 3.3. Сравнительные модели

Результаты для MLP+, PNN и Autoint сравниваются с:

1)    логистической регрессией (LR);

2)    деревьями решений с градиентным усилением, в частности, LightGBM (Ke и др., 2017);

3)    простой модели MLP, созданной путем удаления слоев из модели TabTransformer (см. (Хуан и др. 2020), §3.1, параграф 1);

4)    Asparse MLP, основанный на (Моркос и др., 2019) • TabTransformer (Хуан и др., 2020);

5)    TabNet (Арик и Пфистер 2020);

6)    узким местом в вариационной информации (VIB) (Алеми и др., 2017).

Результаты для этих моделей взяты из (Huang et al., 2020).

 3.4 Результаты

В таблице 1 приведены общие средние значения AUROC для каждой из моделей во всех наборах данных. Для каждого отдельного набора данных среднее значение AUROC по складкам перекрестной проверки приведено в таблице 2. Эти таблицы показывают, что MLP+, PNN и AutoInt конкурируют с любой из моделей сравнения. Фактически, результаты показывают, что эти модели превосходят другие модели. Autoint, PNN и MLP+ имеют наибольшие общие средние баллы AUROC, а для 10 из 15 наборов данных AUTOINT имеет наибольший индивидуальный AUROC или привязан к наибольшему (округлено до 3 цифр). В частности, Autoint, PNN и MLP+, похоже, превосходят недавно представленные модели TabTransformer и TABNET. Однако производительность модифицированного PNN, возможно, немного разочаровывает, поскольку он содержит два блока MLP+, но в целом работает лишь немного лучше, чем модель MLP+ с одним блоком MLP+.

Всегда важно учитывать, как обобщаются подобные результаты. Наборы данных и настройка эксперимента были взяты из (Huang et al. 2020) специально для того, чтобы избежать выбора, который потенциально благоприятствовал новым моделям, например, TabTransformer или Tabnet. Однако есть и другие детали, которые могут повлиять на сравнение; некоторые могут отдать предпочтение AutoInt, PNN и MLP+, некоторые могут отдать предпочтение другим моделям.

Другое пространство поиска параметров. Например, возможные значения отсева для AutoInt, MLP+ и PNN составляли 0,0, 0,25, 0,50, 0,75, но для других моделей глубокого обучения значения отсева были 0.0,0.1,0.2,...,0.5.

Различные случайные начальные значения использовались для разделения набора данных для AutoInt, MLP+ и PNN по сравнению с другими моделями. Здесь были использованы два случайных начальных значения и усреднены результаты, чтобы попытаться уменьшить любую большую разницу из-за начального значения. Однако возможно, что разделение данных здесь более выгодно, чем в оригинале, или наоборот.

Для TabTransformer, в дополнение к 20 испытаниям HPO, на модель для разделения данных, было использовано 50 начальных раундов (итераций) оптимизации гиперпараметров на 5 наборах данных для определения размеров MLPLAYER и некоторых значений параметров TabTransformer. Для новых моделей не использовались начальные раунды оптимизации. Вместо этого, для определения размера партии и размера выборочной партии было использовано несколько ручных испытаний (гораздо меньше 50).

При сравнении моделей глубокого обучения с моделями здесь использовались различные категориальные вложения. Кроме того, новые модели имеют дополнительное некатегориальное встраивание. Здесь принято считать, что эти вложения являются частью модели, но также разумно рассматривать вложения отдельно от остальной части модели.

Общая установка эксперимента (опять же, скопирована из документа TabTransformer (2019, 2020)), с 20 испытаниями байесовского HPO на модель за раз, с периодом, выбранным валидацией AUROC вместо использования заданного количества периодов или итераций. При этом все задачи являются задачами двоичной классификацией и это может благоприятствовать некоторым моделям по сравнению с другими.

 4. Абляция

В таблице 3 показана производительность наших моделей, которые представляют собой приближенный переход от простого MLP к автоматической настройке. Первая модель - это базовый MLP (Huang, 2020 г.). Во-вторых, MLP_FF создается из модели MLP+ путем удаления слоев категорий skip и Leakygate (индекс MLP_FF означает skip= False, gate=False), то есть модель, изображенная на рисунке 1a, но с GhostBatchNorm. Далее следует модель MLP+. Наконец, модифицированная модель AutoInt, показанная на рисунке 3b, которая включает структуру MLP+, но добавляет второй столбец с LeakyGate, блоком самоконтроля и вторым блоком MLP+.

В таблице 3 приведено общее среднее значение AUROC вместе с AUROC для каждого набора данных и коэффициентом усиления по сравнению с предыдущей моделью слева направо. Общее среднее значение улучшается для каждой последующей модели, и в большинстве отдельных наборов данных последующая модель улучшает предыдущую модель или связана с ней. Однако общий выигрыш уменьшается с каждой последующей моделью.

Разница в структуре между моделями AutoInt и MLP+ велика, как видно из сравнения рисунка 1b и рисунка 3b. Существует также много различий между базовым MLP и MLP_FF:

1)    базовый MLP от (Huangetal.2020) использует активацию SELU (Klambaueretal.2017), MLP_FF использует протекающий ReLU;

2)    базовый MLP использовал пакетную норму, MLP_FF использует Пакетную нормализацию выборки;

3)    пространство поиска для линейных размеров слоев и скорости отсева отличалось в (Huangetal.2020) по сравнению с приведенным здесь (подробную информацию о пространстве поиска см. в таблице 7 приложения).

Все эти детали реализации для MLP_FF также применимы к модифицированным моделям MLP+, PNN и Autoint. В таблице 4 суммируется еще одно удаление, начиная с полностью модифицированных моделей и заканчивая версиями, которые удаляют утечки и пропускной слой. Для всех трех моделей лучше всего подходит полностью модифицированная версия. Для MLP+, удаление пропускного слоя лучше, чем удаление пропускного слоя, и LeakyGate, как и следовало ожидать. Однако для PNN это наихудший вариант, а для Autoint это равносильно удалению как слоя пропуска, так и LeakyGate.

Таблица 10 приложения включает оценки для всех трех версий для всех наборов данных.

Можно было бы провести еще много вариантов абляции, чтобы протестировать больше подмножеств предлагаемых модификаций. Однако общий вывод из текущих результатов абляции заключается в том, что предлагаемые модификации улучшают модели и хорошо работают вместе.

 5. Интерпретация выходных данных LeakyGate (Дырявые ворота).

LeakyGate представляет собой комбинацию поэлементного линейного преобразования и LeakyReLU. Первый слой будет масштабировать, переводить и/или переворачивать значения каждого столбца независимо от других столбцов. LeakyReLU пропустит любое положительное значение без изменений и нивелирует любые отрицательные значения почти до нуля. Другими словами, если w_i и b_i являются параметрами линейного слоя для i-го столбца, то эффект затвора для столбца i равен

В первом случае значение «проходит насквозь», т.е. значение проходит нетронутым, а во втором случае оно «просачивается». В зависимости от знаков w_i и b_i, параметры ворот показывают, что значения столбца разделены между проходом через ворота или утечкой, таблица 5.

Такое разделение LeakyGate на самом деле является мотивацией для этого. LeakyGate предназначен для того, чтобы действовать как простой фильтр или в качестве маски с потенциально различным поведением для каждого столбца, и где маскировка зависит от каждого отдельного значения в столбце. Основной эффект и цели аналогичны маскировке в TabNet (Arik и Pfister 2020). Одним из приятных следствий фильтрации является то, как она потенциально может помочь интерпретации модели различными способами, например, помочь с отдельным этапом выбора функции или интерпретацией результатов в зависимости от конкретного случая.

Пример, связанный с выбором объекта. Модель MLP+ подходит для базового набора данных о спаме из раздела 3. Этот набор данных не имеет категориальных признаков. Для экспериментов все объекты были встроены в многомерное пространство, но в этом примере объекты не встроены. В остальном все аспекты процесса подгонки такие же, как и в экспериментах: двадцать итераций байесовской гиперпараметрической оптимизации в одном и том же пространстве параметров и т.д.

В модели MLP+ есть две уязвимости: одно перед блоком MLP и одно перед слоем пропуска, рис. 1b. поскольку данные не встроены, каждый столбец ввода в отверстие для утечки является исходным столбцом данных. Для каждого из Leakygates и для каждого столбца мы можем подсчитать, сколько значений прошло через ворота по сравнению с утечкой, посмотрев на знак значения непосредственно перед LeakyReLU, либо непосредственно после. Если значение положительное, оно прошло через него.

На рисунке 4 показан, столбец за столбцом, процент строк, которые были положительными после каждой утечки. Столбцы сортируются по проценту строк, в которых два Leakygates согласуются положительным или отрицательным образом (они согласованы, если оба положительны или оба не положительны, в противном случае они не согласованы). На нижнем графике мы видим диапазон согласия от 100% слева до 0% справа. На самом деле, для десяти столбцов существует полное согласие, а для двух столбцов - полное несогласие. В таблице 6 приведены некоторые из тех же значений, и их, возможно, будет легче интерпретировать.

Из верхнего графика рисунка 4 или из таблицы 6 столбцы с номерами 8 и 9 не имеют положительных значений ни после одного из элементов. Это говорит о том, что эти столбцы практически не влияют на результат MLP+. Следовательно, они являются отличными кандидатами для отбрасывания. Фактически, после их удаления и перегруппировки AUROC улучшился с 0,977 до 0,979. Этот AUROC не так хорош, как был получен при внедрении столбцов, таблица 2, но, несмотря на это, пример демонстрирует потенциал метода. Тот же метод, возможно, можно было бы применить к встроенным столбцам, чтобы удалить ненужные размеры встраивания.

 

6. Сопутствующая работа

MLP с регуляризацией. Совсем недавняя статья (Kadra etal.2021) показала, что MLP с «коктейлем» стратегий регуляризации могут обеспечить отличную производительность. В этой статье архитектура MLP была исправлена, а оптимизация сосредоточена на выборе методов регуляризации из пяти категорий:

1)    уменьшение веса, например, регуляризация L₁,L₂;

2)    увеличение данных, например, Вырезание (DeVriesand Taylor 2017) и смешивание (Zhangetal.2018);

3)    усреднение модели, например, отсев и явное среднее значение моделей;

4)    структурная и линеаризация, например, пропуски.

5) неявная, например, пакетная нормализация.

Подход был протестирован на большом наборе наборов данных и получил лучшую общую производительность, чем GBDTS от XGBoost (Ченанд Гестрин 2016) и такие модели, как Tabnet, Ансамбли нейронных решений (NODE), (Попов, Морозов и Бабенко 2019) и DNF-Net (Абутбул и др. 2020).

Есть много общего между этими результатами и результатами здесь. Модели MLP+, PNN и Autoint содержат методы из 3 из 5 категорий регуляризации: отсев, пропуски, пакетная нормализация (с помощью пакетной нормализации) и явное усреднение подкомпонентов. Результаты здесь показали, что модифицированный MLP+  выполнял GBDT (но с использованием Light GBM вместо XGBoost). Приведенные здесь результаты делают еще один шаг вперед и показывают, что модификации, используемые для MLP+, улучшают другие табличные модели нейронных сетей.

Основной урок из (Kadra et al. 2021) для текущего подхода, по-видимому, заключается в том, что следует протестировать больше стратегий регуляризации в сочетании с уже используемыми здесь методами. Это отличный вариант для будущего исследования.

Другие сравнения GBDT Аналогичным образом (Шварц-Зив и Армон 2021) сравнили XGBoost GBDT с TABNET, NODE, DNF-Net и 1D-CNN, моделью, представленной в конкурсе Kaggle (Baosenguo 2021). Наборы данных состояли из девяти наборов данных, взятых из документов Tabnet, NODE и DNF-Net, трех наборов данных из каждой статьи и двух наборов данных, которые не появлялись ни в одной из статей (наборы данных shrutime и blastchar, также используемые в данной статье). Результаты показывают, что GBDT, как правило, превосходят любую отдельную ранее рассмотренную нейронную сеть. Еще одним интересным открытием является то, что недавние нейронные сети, как правило, намного лучше работают с наборами данных из их собственных работ. Другими словами, недавние табличные нейронные сети, на которые они смотрят, похоже, плохо обобщаются. Один из уроков, который следует извлечь, заключается в том, что представленные здесь модифицированные модели должны быть протестированы на множестве дополнительных наборов данных.

Больше сравнений GBDT и другая модель трансформатора. В другой недавней статье (Горишний и др., 2021) сравниваются GBDT и табличные нейронные сети, утверждается, что GBDT и нейронные сети хорошо справляются с разными задачами. В нем используются GBDT из XGBoost и CatBoost (Прохоренкова и др., 2018), а также Tabnet, NODE, Autoint (не модифицированная версия, используемая в текущей статье) и другие модели нейронных сетей. Модели нейронных сетей работали лучше, когда данные были «однородными», когда понятия, измеренные в данных, были одинаковыми или очень похожими от объекта к объекту. Например, изображения с расположением каждого пикселя в виде отдельного поля были бы однородными. GBDTS работали лучше, когда функции были «гетерогенными». Например, данные о жилье, в которых записывается количество комнат, количество спален, площадь и т.д.

Они также обнаружили, что ResNet, хотя изначально и не задумывалась как табличная модель, превосходит последние модели. Наконец, они представили новую модель на основе трансформатора под названием FT-Transformer, которая превзошла ResNet и другие нейронные сети, но в целом превзошла GBDT только в однородных наборах данных.

В результате, недавние табличные нейронные сети работают хуже, чем GBDT, поддерживаемые (Huang et al. 2020), которые являются источником сравнительных данных в текущей статье. Это видно из таблицы 1, где GBDT превосходят все модели, не выделенные жирным шрифтом, судя по общему среднему значению AUROC. Конечно, таблица 1 также предполагает, что представленные здесь модифицированные модели действительно работают лучше, чем GBDT, если результаты здесь обобщены. Это также не тот случай, когда представленные здесь модели, как правило, хуже работают с разнородными данными. Некоторые из отдельных наборов данных, в которых они показывают наилучшие результаты, неоднородны, например, 1995 income, shrutime, insurance co, qsar bio (см. таблицу 2).

 7. Заключение

В данной статье предлагается несколько модификаций табличных нейронных сетей. Эти модификации, вероятно, полезны для многих моделей, но для демонстрации используются три существующие модели: MLP, PNN и AutoInt. Эксперименты с 15 наборами данных и сравнение с семью другими моделями показывают, что модифицированные модели конкурируют или превосходят недавние табличные нейронные сети и GBDT от LightGBM. Исследование вариаций модели с меньшим количеством модификаций показывает, что предложенная комбинация работает хорошо.

 

---

Ссылки

Abutbul, A.; Elidan, G.; Katzir, L.; and El-Yaniv, R. 2020.
DNF-Net: A Neural Architecture for Tabular Data. ArXiv:
2006.06465 [cs.LG].

Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; and Koyama, M.
2019. Optuna: A Next-generation Hyperparameter Optimization Framework. ArXiv: 1907.10902 [cs.LG].

Alemi, A. A.; Fischer, I.; Dillon, J. V.; and Murphy, K. 2017.
Deep Variational Information Bottleneck. International
Conference on Learning Representations abs/1612.00410.
URL https://arxiv.org/abs/1612.00410. ArXiv: 1612.00410
[cs.LG].

Arik, S. O.; and Pfister, T. 2020. TabNet: Attentive Interpretable Tabular Learning. URL https://arxiv.org/abs/1908.
07442. ArXiv: 1908.07442 [cs.LG].

Baosenguo. 2021. baosenguo/Kaggle-MoA-2nd-PlaceSolution. URL https://github.com/baosenguo/Kaggle-MoA2nd-Place-Solution.

Bradley, A. P. 1997. The use of the area under the ROC curve
in the evaluation of machine learning algorithms. Pattern
recognition 30(7): 1145–1159.

Chen, T.; and Guestrin, C. 2016. Xgboost: A scalable tree
boosting system. In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining, 785–794.

Cheng, H.-T.; Koc, L.; Harmsen, J.; Shaked, T.; Chandra, T.;
Aradhye, H.; Anderson, G.; Corrado, G.; Chai, W.; Ispir, M.;
Anil, R.; Haque, Z.; Hong, L.; Jain, V.; Liu, X.; and Shah,
H. 2016. Wide & Deep Learning for Recommender Systems.
ArXiv: 1606.07792 [cs.LG].

DeVries, T.; and Taylor, G. W. 2017. Improved Regularization of Convolutional Neural Networks with Cutout. ArXiv: 1708.04552 [cs.CV].

Dimitriou, N.; and Arandjelovic, O. 2020. A New Look at
Ghost Normalization. ArXiv: 2007.08554 [cs.CV].

Erickson, N.; Mueller, J.; Shirkov, A.; Zhang, H.; Larroy, P.;
Li, M.; and Smola, A. 2020. AutoGluon-Tabular: Robust and
Accurate AutoML for Structured Data. ArXiv: 2003.06505
[stat.ML].

Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; and Babenko, A.
2021. Revisiting Deep Learning Models for Tabular Data.
ArXiv: 2106.11959 [cs.LG].

Guyon, I.; Sun-Hosoya, L.; Boulle, M.; Escalante, H. J.; ´
Escalera, S.; Liu, Z.; Jajetic, D.; Ray, B.; Saeed, M.; Sebag, M.; Statnikov, A.; Tu, W.; and Viegas, E. 2019. Analysis of the AutoML Challenge series 2015-2018. In AutoML, Springer series on Challenges in Machine Learning. URL https://www.automl.org/wp-content/uploads/2018/09/chapter10-challenge.pdf.

He, K.; Zhang, X.; Ren, S.; and Sun, J. 2015. Deep Residual Learning for Image Recognition. ArXiv: 1512.03385
[cs.CV].

Hoffer, E.; Hubara, I.; and Soudry, D. 2018. Train longer,
generalize better: closing the generalization gap in large batch
training of neural networks. ArXiv: 1705.08741 [stat.ML].

Huang, T.; Zhang, Z.; and Zhang, J. 2019. FiBiNET. Proceedings of the 13th ACM Conference on Recommender Systems doi:10.1145/3298689.3347043. URL http://dx.doi.org/10.1145/3298689.3347043.

Huang, X.; Khetan, A.; Cvitkovic, M.; and Karnin, Z. 2020.
TabTransformer: Tabular Data Modeling Using Contextual
Embeddings. ArXiv: 2012.06678 [cs.LG].

Kadra, A.; Lindauer, M.; Hutter, F.; and Grabocka, J. 2021.
Regularization is all you Need: Simple Neural Nets can Excel
on Tabular Data. ArXiv: 2106.11189 [cs.LG].

Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.;
Ma, W.; Ye, Q.; and Liu, T.-Y. 2017. LightGBM: A
highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems, 3146–
3154. URL https://papers.nips.cc/paper/6907-lightgbm-ahighly-efficient-gradient-boosting-decision-tree.pdf.

Kingma, D. P.; and Ba, J. 2017. Adam: A Method for
Stochastic Optimization. ArXiv: 1412.6980 [cs.LG].

Klambauer, G.; Unterthiner, T.; Mayr, A.; and Hochreiter, S.
2017. Self-normalizing neural networks. In Advances in neural information processing systems, 971–980.

Lian, J.; Zhou, X.; Zhang, F.; Chen, Z.; Xie, X.; and Sun, G.
2018. xDeepFM. Proceedings of the 24th ACM SIGKDD
International Conference on Knowledge Discovery & Data
Mining doi:10.1145/3219819.3220023. URL http://dx.doi.
org/10.1145/3219819.3220023.

Maas, A. L.; Hannun, A. Y.; and Ng, A. Y. 2013. Rectifier
nonlinearities improve neural network acoustic models. In
in ICML Workshop on Deep Learning for Audio, Speech and
Language Processing.

Morcos, A. S.; Yu, H.; Paganini, M.; and Tian, Y. 2019. One
ticket to win them all: generalizing lottery ticket initializations across datasets and optimizers URL http://arxiv.org/abs/1906.02773. ArXiv:1906.02773 [cs, stat].

Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.;
Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga,
L.; Desmaison, A.; Kopf, A.; Yang, E.; DeVito, Z.; Raison,
M.; Tejani, A.; Chilamkurthy, S.; Steiner, B.; Fang, L.; Bai,
J.; and Chintala, S. 2019. PyTorch: An Imperative Style,
High-Performance Deep Learning Library. In Wallach, H.;
Larochelle, H.; Beygelzimer, A.; d’Alche Buc, F.; Fox, E.; ´
and Garnett, R., eds., Advances in Neural Information Processing Systems 32, 8024–8035. Curran Associates, Inc. URL
http://papers.neurips.cc/paper/9015-pytorch-an-imperativestyle-high-performance-deep-learning-library.pdf.

Popov, S.; Morozov, S.; and Babenko, A. 2019. Neural Oblivious Decision Ensembles for Deep Learning on Tabular Data.
ArXiv: 1909.06312 [cs.LG].

Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A. V.;
and Gulin, A. 2018. CatBoost: unbiased boosting with categorical features. In Advances in neural information processing systems, 6638–6648.
Qu, Y.; Cai, H.; Ren, K.; Zhang, W.; Yu, Y.; Wen, Y.; and
Wang, J. 2016. Product-based Neural Networks for User Response Prediction. ArXiv: 1611.00144 [cs.LG].

Shwartz-Ziv, R.; and Armon, A. 2021. Tabular Data: Deep
Learning is Not All You Need. ArXiv: 2106.03253 [cs.LG].

Song, W.; Shi, C.; Xiao, Z.; Duan, Z.; Xu, Y.; Zhang, M.;
and Tang, J. 2019. AutoInt: Automatic Feature Interaction
Learning via Self-Attentive Neural Networks. Proceedings
of the 28th ACM International Conference on Information
and Knowledge Management - CIKM ’19 1161–1170. doi:
10.1145/3357384.3357925. URL http://arxiv.org/abs/1810.11921. ArXiv: 1810.11921.

Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.;
Gomez, A. N.; Kaiser, Ł.; and Polosukhin, I. 2017. Attention
is all you need. In Advances in neural information processing
systems, 5998–6008.

Wang, R.; Fu, B.; Fu, G.; and Wang, M. 2017. Deep &
Cross Network for Ad Click Predictions. ArXiv: 1708.05123
[cs.LG].

Zhang, H.; Cisse, M.; Dauphin, Y. N.; and Lopez-Paz, D.
2018. mixup: Beyond Empirical Risk Minimization. ArXiv:
1710.09412 [cs.LG].