Вместо вступления

Тригонометрические функции, характеризующиеся высоким потреблением процессорного времени, могут негативно влиять на выбор бюджетных микроконтроллеров ( без модуля FPU ) для задач, где важна скорость счёта, например, контроль пространственного положения.
Библиотечные тригонометрические функции с двойной точностью в два раза медленнее, чем с одинарной. Это досадный факт.
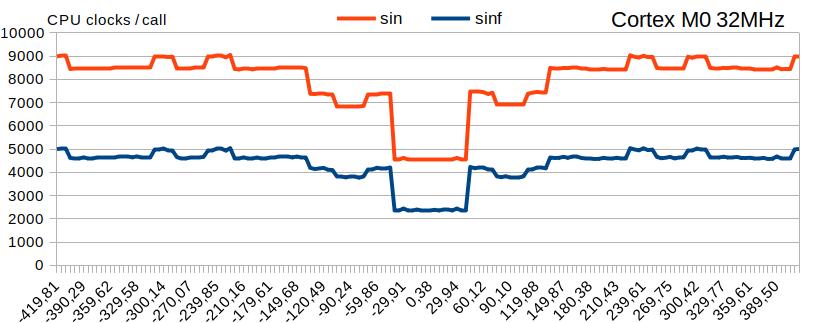
На иллюстрации время работы «sin()» и «sinf()», измеренное в тактах CPU, на диапазоне [-420° .. +420°] с шагом 5°, плюс слабый шум.

Производительность библиотечных «sin()» и «sinf()» высока вблизи точки «0» и снижается в два раза пропорционально модулю аргумента.
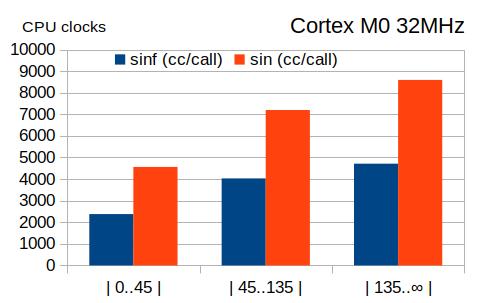
Возникает потребность считать тригонометрию несколько быстрее, без FPU, но допуская худшую точность:
у аргумента — в пределах чувствительности доступных электронных датчиков положения, например, LSM6DSO;
у результата — в пределах точности доступных шаговых двигателей и сервомашин, например, HS-5082MG.
Требования к алгоритму
Требования к исходному коду:
a) Исходный код без интеллектуального балласта третьих лиц;
b) Самодостаточный компилируемый модуль на основе стандартных библиотек;
c) Кросс-платформенность — отсутствие вставок на ассемблере.Требования к исполняемому коду:
a) Ограниченный объём бинарного кода — чем меньше, тем лучше;
b) Ограниченный объём статических и динамических данных — чем меньше, тем лучше.Требования к интерфейсу (привычный):
a) float sint( float x );
b) float cost( float x ).Требования к аргументу:
a) Объектная сущность: геометрический плоский угол;
b) Единица измерения: угловой градус в десятичном виде: 1,0 °;
c) Точность измерения: +/- 0,05 °;
d) Рабочий диапазон: +/- 5400 °;
e) Тип данных: float, согласно IEEE 754.Требование к результату:
a) Объектная сущность: тригонометрические функции «sin» и «cos»;
b) Точность счёта: +/- 0,005;
c) Тип данных: float, согласно IEEE 754.
Применяемая методика
Сравнительный анализ способов приближения тригонометрических функций за границами настоящей публикации.
Применяемый метод считает синус плоского угла в рабочем диапазоне от 0 до ½π.
Синусы углов за пределами рабочего диапазона находятся через осевую симметрию применительно к результату из рабочего диапазона.
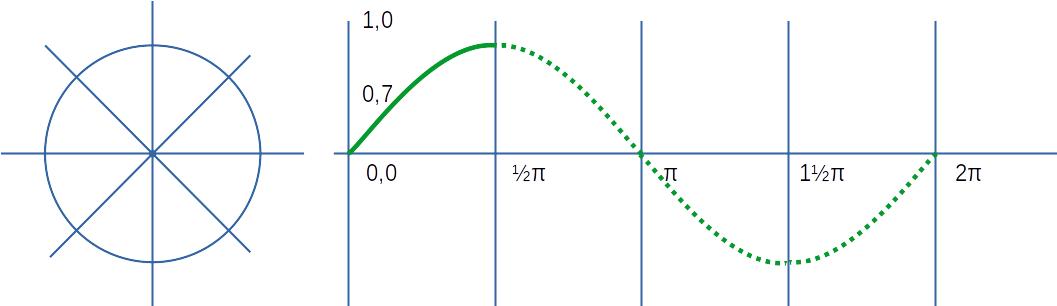
Вычисление синуса угла в рабочем диапазоне заменяется поиском точки на куске одномерного сплайна:

В некоторых условиях сплайн и синус демонстрируют схожее поведение.

Аппроксимирующий сплайн представляется формой Безье. Точка сплайна вычисляется геометрически, редуцированным методом де Кастельжо.
Алгоритм оптимизируется на соответствие функции синус.
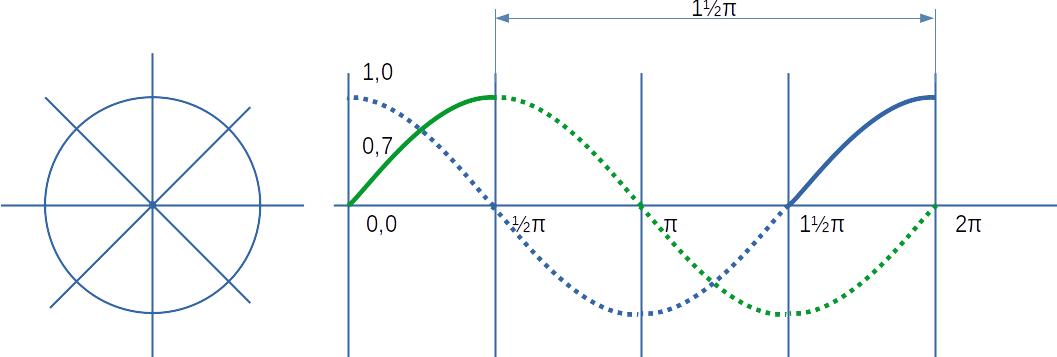
Косинус считается как синус, сдвинутый по фазе на 1½ π.
Достигнутый результат
Характеристики бинарного кода на платформе Cortex M0:
размер бинарного кода — 168 байт;
размер стека — 40 байт (локальные переменные — 24 байта);
статическая и динамическая память — без надобности.
Результат с тремя точными знаками после запятой и гарантированной ошибкой в четвёртом знаке — | 0,0003 |.
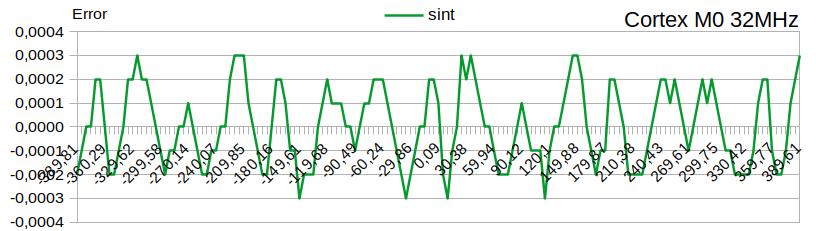
Скорость работы вновь созданной функции на платформе Cortex M0 превосходит библиотечные «sin» и «sinf» в 10 и более раз.
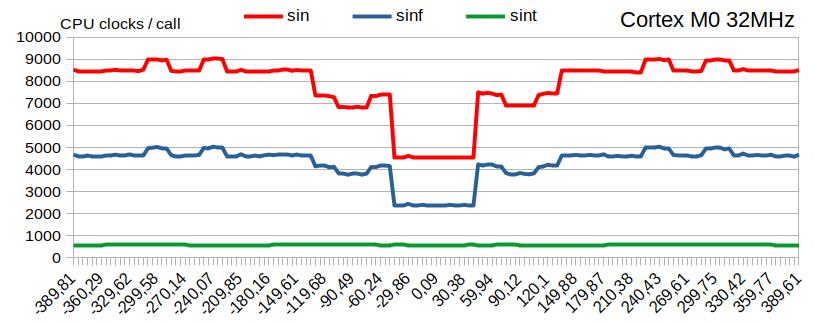
У алгоритма есть опции, выбираемые через условную компиляцию:
медленный счёт — гарантирует ошибку |0,0003| и менее;
быстрый счёт — даёт преимущество в ~20 тактов на Cortex M0, ухудшая ошибку до |0,0004|.
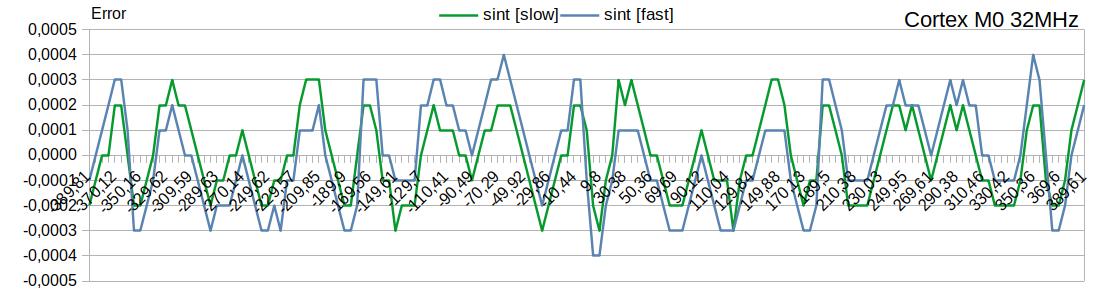
Преимущество в 15-25 тактов ( ~1us ) — это существенный прирост производительности для бюджетных контроллеров на малых частотах.

На платформе Cortex M4 быстрый метод счёта даёт сомнительное преимущество в 3-5 тактов, соразмерное погрешности измерения, и ухудшение точности до |0,0004|.
В целом, тестирование алгоритма на Cortex M4 показало приемлемый результат с малым превосходством по скорости библиотечной функции «sinf», оптимизированной под имеющийся FPU.
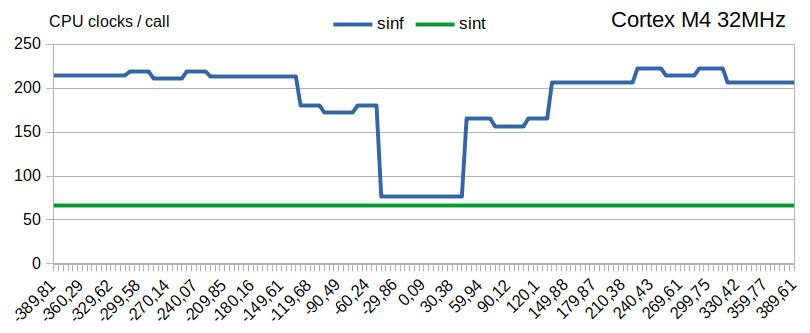
На графике отсутствует функция «sin» [ double sin ( double x ) ], показывающая худшее на десятичный порядок время.
На платформе Cortex M4 каждый вызов «sin» [ double sin ( double x ) ] забирает порядка 2500 тактов.
Итоговый алгоритм допускает аргумент в угловых градусах и в радианах.
Выбор единицы измерения аргумента осуществляется через условную компиляцию.
Вместо заключения
Алгоритм соответствует техническим требованиям, показывая удовлетворительную скорость и ожидаемую точность счёта.
Есть некоторый потенциал для улучшения характеристик алгоритма. С практической точки зрения этот потенциал целесообразно отложить в будущее.
Прикладная библиотека
Файл заголовок
/******************************************************************************
* File: cosint.h Created on 31 мар. 2022 г.
*
* Copyright (c) 2022, "Nikolay E. Garbuz" <nik_garbuz@list.ru>
*
* This program is free software: you can redistribute it and/or modify
* it under the terms of the GNU General Public License version 3 as
* published by the Free Software Foundation.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*
* You should have received a copy of the GNU General Public License
* along with this program. If not, see <http://www.gnu.org/licenses/>.
*
* Authored by "Nikolay E. Garbuz" <nik_garbuz@list.ru>
* Modified by
*
* TAB Size .EQ 4
********************************************************************************/
#ifndef _COSINT_H_
#define _COSINT_H_
#ifdef __cplusplus
extern "C"
{
#endif
//**********************************************************
//---------------- module interface ------------------------
/**
* @brief Fast sine function for approximate calculations
* @param Geometric angle between -5400.00 and 5400.00 degrees
* with two correct numbers after the decimal separator
* @retval Sine with three correct numbers after the decimal separator
*/
float sint( float x );
/**
* @brief Fast cosine function for approximate calculations
* @param Geometric angle between -5400.00 and 5400.00 degrees
* with two correct numbers after the decimal separator
* @retval Cosine with three correct numbers after the decimal separator
*/
float cost( float x );
//**********************************************************
//---------------- module options --__----------------------
/*
* The [COSINT_RAD] directive sets the angle units.
* By default, module functions take a parameter measured in degrees.
*
* Remove or comment out the [#undef COSINT_RAD] line
* to switch the interface [cosint] from degrees to radiant.
*/
#define COSINT_RAD
#undef COSINT_RAD
/*
* The [COSINT_FAST] directive defines the linear proportion method.
* The default is the slow method with a maximum error modulus is |0.0003|.
*
* Remove or comment out the [#undef COSINT_FAST] line to switch module [cosint] to fast mode.
* About ~1.6% speedup, maximum error modulus is 0.0004
*/
#define COSINT_FAST
#undef COSINT_FAST
#ifdef __cplusplus
}
#endif
#endif /* _COSINT_H_ */Исходный код
/******************************************************************************
* File: cosint.c Created on 31 мар. 2022 г.
*
* Copyright (c) 2022, "Nikolay E. Garbuz" <nik_garbuz@list.ru>
*
* This program is free software: you can redistribute it and/or modify
* it under the terms of the GNU General Public License version 3 as
* published by the Free Software Foundation.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*
* You should have received a copy of the GNU General Public License
* along with this program. If not, see <http://www.gnu.org/licenses/>.
*
* Authored by "Nikolay E. Garbuz" <nik_garbuz@list.ru>
* Modified by
*
* TAB Size .EQ 4
********************************************************************************/
#pragma GCC push_options
#pragma GCC optimize ("O3")
#include "cosint.h"
#include <stdint.h>
//**********************************************************
//---------------- module implementation -------------------
typedef enum
{
coname = -1, siname
} EFName;
inline float cosint( float x, EFName fn );
//---------------- exported module functions ---------------
float sint( float x )
{
return cosint( x, siname );
}
float cost( float x )
{
return cosint( x, coname );
}
//**********************************************************
//------------- helper data and function -------------------
#ifndef M_PI
# define M_PI 3.14159265358979323846 /* pi */
#endif
#ifdef COSINT_RAD
# define R_UNIT M_PI
#else
# define R_UNIT 180.
#endif
#define R_TU ( R_UNIT / 2. ) // The real measure unit in use
#define M_PRC 0x0A // The precision of calculations
#define M_MAX 0x1F // The bit range of calculations
#define M_DAT ( M_MAX >> 1 ) // The bit range of a data
#define M_SGN 0x02 // The sign mask for a result of calculations
#define M_QTR 0x01 // The mask of a circle quarter
#define M_ASQ ( M_SGN | M_QTR ) // The mask of common characteristics for the angular data
#define M_ADV ( 1 << M_DAT ) // The allowed data value
#define M_ADM ( M_ADV - 1 ) // The mask of allowed data value
#define M_MTR (int32_t)( ( M_ADV << M_PRC ) / R_TU )
// Slow and precise, maximum error modulus is |0.0003|
#define DO_SLOW( t, pw, A, B ) ( ( ( t * ( B - A ) + ( ( 1 << pw ) - 1 ) ) >> pw ) + A )
// Fast and rough, about ~1.6% speedup, maximum error modulus is |0.0004|
#define DO_FAST( t, pw, A, B ) ( ( ( t * ( B - A ) ) >> pw ) + A )
#ifdef COSINT_FAST
# define LN_ DO_FAST
#else
# define LN_ DO_SLOW
#endif
// Control data for the spline
#define Ax 0x0000
#define Bx 0x320B
#define Cx 0x655D
#define Dx 0x8000
// helper function
float cosint( float x, EFName fn )
{
int32_t sq, tm;
int32_t A, B, C, D;
// Converting from real to integer
tm = M_MTR;
tm *= x;
tm = tm >> M_PRC;
// Choosing a function via a phase shift by it name
tm += fn & ( M_ADM );
// Extracting a quarter of the angle and a sign of the result
sq = ( tm >> M_DAT ) & M_ASQ;
// Removing periods and reverse from the angle value
// Transforming the angle value to the first quarter
if ( sq & M_QTR )
tm = ( tm & M_ADM ) ^ M_ADM;
else
tm &= M_ADM;
// Calculating a result thru a line proportion
A = Dx;
B = LN_( tm, M_DAT, Cx, Dx );
C = LN_( tm, M_DAT, Bx, Cx );
D = LN_( tm, M_DAT, Ax, Bx );
A = LN_( tm, M_DAT, B, A );
B = LN_( tm, M_DAT, C, B );
C = LN_( tm, M_DAT, D, C );
A = LN_( tm, M_DAT, B, A );
B = LN_( tm, M_DAT, C, B );
A = LN_( tm, M_DAT, B, A );
// Correcting a numeric sign of the result
x = ( sq & M_SGN ) ? -A : A;
// Converting from integer to real and return
x /= M_ADV;
return x;
}
#pragma GCC pop_optionsКомментарии (82)

AAbrosov
05.04.2022 11:45Может я что-то путаю, но мне всегда казалось что тригонометрические функции - периодические с периодом 2 пи. И считать углы нужно в интервале от 0 до пи/2 ?

numeric Автор
05.04.2022 12:19Вы абсолютно правы,
если рассматривать тригонометрические функции обособленно и раздельно.Если рассматривать совместно, включая аппроксимирующую функцию, то общим оказывается только квадрант.
Тогда, значения за диапазоном квадранта вычисляются методами осевой симметрии и сдвигом фаз (смена математического знака, сложение с константой).
Да, существенна-ли разница, как считать, если результат счёта удовлетворительный.

AAbrosov
05.04.2022 16:03Тут на половине графиков все цифры точно такие-же непонятные.
Синус имеет период 2 пи. Четверть от периода с уникальными значениями пи/2.
Вы тут какую-то свою функцию вычисляете судя по всему.
(скорее всего sin(2x))
numeric Автор
05.04.2022 16:26На графиках:
- на оси абсцисс отложена уголовая величина, измеренная в градусах угловой дуги;
- на оси ординат показаны время срабатывания функции, измеренное в тактах CPU, или ошибка вычисления, как разница между значением, возвращённым библиотечной функцией sinf, и результатом, возвращённым функцией приближённого вычисления sint.
AAbrosov
05.04.2022 16:40Неправильные графики с синусами у вас в разделе "Применимая методика".
Кстати, наверное это ПрименЯЕмая методика. А в коде всё хорошо
#ifdef COSINT_RAD
# define R_UNIT M_PI
#else
# define R_UNIT 180.
#endif
#define R_TU ( R_UNIT / 2. ) // The real measure unit in use
Расчёты идут для пи/2=90°
numeric Автор
05.04.2022 19:32Работа над ошибками проведена!
Огромное спасибо Вам за внимание к моей работе и конструктивные замечания.

boscholeg
05.04.2022 11:56+2Поясните почему важно использование постоянно вычисляемых значений для синуса или косинуса. Почему нельзя один раз не спеша вычислить все нужные значения и занести в таблицу. И больше не тратить время на вычисление?

static_cast
05.04.2022 12:00+5Память. Для микроконтроллеров особенно чувствительно. Для "взрослых" процессоров, к тому же, не имеет смысла и по скорости. А раньше считали, да. Lookup таблицы это техника из тех времён, когда не у всех процессоров был FPU.

boscholeg
05.04.2022 12:28Я признаться думал что у современных МК с памятью уже получше дела обстоят. Тогда все понятно.

DoHelloWorld
05.04.2022 22:55+1В целом табличка на 360 значений выйдет на 1440 байт, если через градус нужна точность. У stm32f0 RAMы не так много, но в целом во flash можно положить с ней не все так плохо, там вроде от 32 КБ.

KvanTTT
06.04.2022 01:30+1360 путем простых преобразований заменяется на 90. А можно вообще использовать 256 градусов для полного угла.

Deosis
06.04.2022 07:12+3Таблицы - это техника из тех времен, когда ещё процессоров не было.


static_cast
06.04.2022 13:25Как говорил наш преподаватель, инженер старой школы: а если вам лень открыть книжку (эти самые таблицы Брадиса), то просто быстренько возьмите на бумажке интерполяционный многочлен Лагранжа второй степени.

abutorin
05.04.2022 12:01Весь вопрос в объёме используемой памяти. Оперативной памяти не так много, а в ПЗУ время доступа большое.

lamerok
05.04.2022 15:16На частототах до 100 МГЦ доступ(чтение) к памяти одинаковый. Это же микроконтроллеры, там вся суть прогу во Флеш залить, иначе смысл программы в ПЗУ.

numeric Автор
05.04.2022 16:34Практика показывает, что на бюджетных микроконтроллерах частота тактирования достаточно ощутимо влияет на время выполнения программы, измеренное в тактах.
Влияние частоты тактироания на скорость выполнения программ зафиксировано здесь: https://habr.com/ru/post/599727/

DarkWolf13
05.04.2022 23:45на одном изделии делали быструю память пзу на базе озу, которые при старте загружались и в дальнейшем шло обращение к зописанным константам в в "постоянном" озу, где были в том числе табличные значения, которые при необходимости уточнялись

staticmain
05.04.2022 12:05Что вы подразумеваете под «нужными» значениями? Например у меня есть игра, в которой персонаж садится в вагонетку на карусели, а её начинает крутить по кругу. Для этого мне нужен как минимум синус рассчитанный для всех возможных углов поворота. Просто 360 значений — будет слишком рвано. Какую цену деления мне следует выбрать заранее?

smoluks4096
05.04.2022 12:16Зачем вы делаете игру на stm32?

staticmain
05.04.2022 12:33+6Я делаю её на MOS 6502, там ситуация еще «лучше» — 3 регистра, 2К памяти, только сложение и вычитание, нет плавающей точки

ksbes
05.04.2022 12:20+2Для всех не нужен — только от 0 до 90. Дальше — как в статье, просто «отражаем» все углы в этот отрезок. Ну а дальше смотрим по точности, которая нам нужна и по алгоритму: берём ближайший или аппроксимируем как-то.
Если с аппроксимацией сплайнами (как в статье), то можно получить очень большую точность, на не очень большом количестве точек (тех же 45 — более чем хватит), но это медленно.
А если хочется быстро, просто выбором из памяти без каких-либо вычислений (кроме отбрасывания двоичных разрядов), то для игры 256 на пипопалам хватит за глаза. А для более серьёзных применений — там будут килобайты и, может, даже, мегабайты (для особых «эстетов»)Зачем вы делаете игру на stm32?
Я делал, как пэт-проект. На основе старого поломанного тетриса.

atd
05.04.2022 12:22Для мелких 8-битных контроллеров обычно так и делали. Но у контроллеров на ARM Cortex поход во флэшку уже не всегда бесплатный, зато более прокачанное АЛУ, и вообще 32 бита.

lamerok
05.04.2022 15:18+1Он не бесплатный с определённой частоты тпм 100 МГЦ, например, думаю в большинстве случаев он бесплатный.

numeric Автор
05.04.2022 12:30+1Бюджетные микроконтроллеры имеют малый размер оперативной памяти, измеряемый в килобайтах.
Когда "на борту" всего 4096 байт (4KB), расходовать ОЗУ на баласт статических данных - это сомнительный путь, если можно быстро посчитать.С другой стороны, представьте задачу на неустойчивое равновесие, например, балансирование вертикальным шестом или управление двух колёсным велосипедом и т.п. Слабо представляю, как заранее предусмотреть все нужные для решения подобных задач значения.

vkni
05.04.2022 18:43+1А скомбинировать подходы, рассчитав "точно", скажем, 10 точек, нельзя? Какой-то хитрой интерполяцией.

numeric Автор
05.04.2022 20:12Допустим.
Но, где смысл, если описаный способ даёт гарантированную точность в любом месте области определения аргумента?
Какой выигрыш даст такая комбинация?

DancingOnWater
05.04.2022 12:26+2Исходный код без интеллектуального балласта третьих лиц;
Я понимаю этот тот самый пресловутый фатальный недостаток? (просто есть на Хабре хорошая статья https://habr.com/ru/post/577256/)
Для чего вам вообще быстрое вычисление синуса? Вы заметили, что невязка у вас смещенная? В реальном мире это практически всегда не есть хорошо.

numeric Автор
05.04.2022 17:49Статья, действительно, интересная. Прочел её вдумчиво и внимательно дважды. Изучил авторский исходный код. Автору плюс.
Автор статьи, Викор Агарков, предлагает всеобъемлющий подход на замечательной теоретической базе, под вполне демократичной лицензией - ссылаться на автора оригинала, создавая производный продукт. В этом проблемы нет.
Думаю, что его решение оптимально для вычислителей среднего и премиального класса.
Здесь же требовалось получить законченное решение, ориентированное на узко-специализированную область, с технологической сложностью на уровне коде-снипета - самодостаточный модуль. Подключил в проект - заработало. Без ассемблерных вставок, статических массивов и внешних генераторов кода.

numeric Автор
05.04.2022 17:50Для чего вам вообще быстрое вычисление синуса?
Вы заметили, что невязка у вас смещенная?
Поясните, пожалуйста, вопросы.

vkni
05.04.2022 18:47Невязка - разница между точной функцией и приближением. Вот, по-моему, она у вас не смещённая.
Чтобы "два раза не вставать" - у вас опечатка в "на соответствие функцие синус" - должно быть "функции". И спасибо за статью.

DancingOnWater
06.04.2022 08:53Про невязку уже сказали, а про смещенность - это то, что ее среднее не ноль. Это плохо, т.к. в ходе вычислений ошибка начинает накапливаться. У полиномов Чебышева такой проблемы нет. Вот код из еще одной статьи:
double Sin7(double x) { x *= 0.63661977236758134308; // 2/Pi int sign = x < 0.0; x = sign ? -x : x; int xf = (int)x; x -= xf; if ((xf & 1) == 1) x = 1 - x; int per = ((xf >> 1) & 1) == 1; double xx = x * x; double y = x * (1.5707903005870776 + xx * (-0.6458858977085938 + xx*(0.07941798513358536 - 0.0043223880120647346 * xx))); return sign ^ per ? -y : y; }В вашем случае не надо считать в double, а нужно перейти на float и остановится на 3-ей степени полинома.

numeric Автор
06.04.2022 10:01Согласен. Вы правы в общем и целом.
В частности, на практических задачах существуют иные ситуации, где исключается влияние накопленной ошибки уже на алгоритмическом уровне: "сигнал получен" -> "сигнал обработан" -> "полёт продолжается".
Более того, ошибка слабо влияет на решение задачи, если скорость вычисления выше инертности системы.
В качестве наглядного примера представим процесс парковки длинного фургона к разгрузочному пандусу:
1) Исполнитель сидит за рулём и слабо различает пространственные границы заднего бампера и разгрузочного пандуса в кривые зеркала заднего вида.2) Руководитель находится сзади фургона, хорошо различает границы, быстро оценивает допустимые пределы, но лишён возможности управления фургоном и точной оценки ситуации "в цифре".
3) Заметим, эта "парочка" легко решает задачу безаварийной паковки к пандусу без измерений и расчётов на калькуляторе.
4) "Назад","Стоп", "Вперёд", "Право", "Правее", "Лево", "Левее" - необходимый и достаточный набор команд Руководителя, понятных Исполнителю, чтобы совершить парковку без аварии за конечное число "шагов" или тактов управления. Ибо погрешность "вычислений" выше инертности системы, а жизненный цикл ошибки "вычислений" ограничен одним шагом.
Вероятно, существует возможность оценивать численную ошибку на каждом шаге управления, оценивать степень её накопления. Но, ускорится ли решение практической задачи парковки, если Руководитель и Исполнитель начнут общаться формально, точно и без ошибок?
- Поверни рулевое колесо на -15 градусов 34 минуты 12 секунд.
- Подай импульс (надави) на педаль акселератора с усилием 2 ньютона в течение 3-х секунд.
- Стоп! Пауза! Оцениваем пространственное положение. А подайте-ка лазерные дальномер и угломер. И калькулятор принесите. Программируемый.:-)
Статистические методы оценки ошибок интересны и увлекательны, как и вся математика в целом. Практика диктует иные подходы. Например, в алгоритме Брезенхема оценка ошибки редуцируется до проверки только знака ошибки. И, это работает.
(imho)
DancingOnWater
07.04.2022 11:31Вариант с накоплением это один лишь из. Допустим, что функция рассогласования это как есть разница между синусом вычисленным и синусом истинным. Казалось бы, абсолютная величина ошибки это 1E-3, а значит и контур у нас жесткий, но смещенность оценки это как добавление к сигналу постоянной величины, и в АЧХ у вас появятся частоты (пусть и с малой амплитудой), в герцовых областях, со ввсеми вытекающими.

numeric Автор
07.04.2022 20:40Согласен. В общем и целом Вы правы.
Прошу пояснить. О каких частотах "со всеми вытекаюшими" Вы предупреждаете?
Если рассуждать в общем и целом с точки зрения механики, то асимметрия - это источник люфта.
Механизм теряет способность к движению, если из него убрать люфт.
Механический люфт - источник вибрации. Вибрация - разрушает механизм, если попадает в его резонанс.
Механизмы служат надёжно и долго, если собственная частота резонанса отличается от рабочей частоты.
Дополнительное страхование рисков преждевременного разрушения механизмов обеспечивают виброгасители и виброопоры.
(imho)

Veresk
05.04.2022 13:16+3Странно что не модифицировали через Чебышева для 45 градусного блока, ограничение в 3-5 членов по операциям плюс минус то же самое даст. Плюс много логических лишних, например ограничение на вводные данные, чем вас не устраивали циклы с отбрасыванием периода? Обычно в таких условиях есть смысл ставить блок рафинирования данных к единому "чистому" входному диапазону значений [0-360), потом четверти получаются также делением на коснтанту.
При рафинировании входных данных не забудьте разрешить коллизию с границами интервала, часто исполнители кода про нее забывают и бывают забавные моменты, когда поворот от 1 градуса до 360 идет путем длинной в 359 градусов.

numeric Автор
05.04.2022 22:30Странно что не модифицировали через Чебышева для 45 градусного блока, ограничение в 3-5 членов
Думал об этом методе. Но, в последний момент появились сомнения в его эффективности в данном конкретном случае. Проверять не стал, применив похожий, но несколько иной способ.
чем вас не устраивали циклы с отбрасыванием периода
Тем, что любой цикл увеличивает расходы, как минимум, на условный переход. А "погоня" за производительностью стала мотиватором для данной работы.
забавные моменты, когда поворот от 1 градуса до 360 идет путем
Согласен.
Но в данном алгоритме подобная ситуация исключена.
Буду признателен, если подскажите тест, который позволит проверить утверждение выше на опубликованном исходном коде.

STMshchik
05.04.2022 13:49+1В каких проектах на МК требуется вычислять синус, косинус? И разве последние жирные stm32 не могут делать это быстро? И были такие критические ситуации когда всё тормозилось на вычислении косинуса, синуса?

iliasam
05.04.2022 14:07+1Как минимум, любое векторное управление моторами требует тригонометрических вычислений.
Существуют различные датчики, где тоже важны тригонометрические вычисления.

numeric Автор
05.04.2022 18:02+1И разве последние жирные stm32 не могут делать это быстро?
Применительно к процессорам Интел и АМД этот алгоритм вообще теряет смысл.
Вопрос лишь в том, стоит ли "стрелять из пушки по воробъям, если есть возможонсть поправить прицел на 'мелкашке' " ?
Здесь про оптимизацию вычислений на бюджетных, сверх дещёвых MPU для тех ситуаций, когда дешевле забыть про дейвайс, чем искать или восстанавливать.
vkni
05.04.2022 18:52Здесь про оптимизацию вычислений на бюджетных, сверх дещёвых MPU для тех ситуаций, когда дешевле забыть про дейвайс, чем искать или восстанавливать.
Это называется технический прогресс - когда для решения каких-то задач используются всё более и более дешёвые средства. :-)

numeric Автор
06.04.2022 21:21Согласен.
Задача технического прогресса - повышать доступность для ширнармас передовых достижений науки и техники.Задача технического прогресса решается через продвижение передовых достижений в массовое производство, как следствие, снижению их себестоимости и цены.
:-)

vkni
06.04.2022 23:25+2Увы, мы отвыкли от настоящего прогресса в сфере ПО, когда программы становятся быстрее и менее требовательны, выполняя всё те же задачи.

premierhr
05.04.2022 14:000,0003 это относительная ошибка или абсолютная? И почему ошибка как функция не симметрична относительно 0?

numeric Автор
05.04.2022 23:130,0003 - это относительная ошибка, разность ( sint() - sinf() ).
Согласно требованиям, указанным в статье, ожидаемая ошибка алгоритма +/- 0,005.
В свою очередь, требование к ошибке +/- 0,005 сформировано на основании точности вероятных исполнительных устройств. Например, у большинства доступных шаговых двигателей паспортная точность 1.8 ° с допуском +/- 0,9 °, т.е. на два порядка хуже алгоритмической.
Таким образом, демонстрация расчётной ошибки с меньшим модулем и разрядом, чем в требованиях [ +/- 0,0003 .vs. +/- 0,005 ], гарантирует удовлетворительную точность для вероятных исполнительных устройств, Гарантирует точность, достижимую простым отбрасыванием младших разрядов без издержек на округление.
В условиях многократного резервирования по точности "борьба" за симметрию расчётной ошибки просто теряет смысл.

premierhr
06.04.2022 06:23это относительная ошибка, разность ( sint() - sinf() ).
Если просто разность, то все-таки это абсолютная погрешность, и на малых углах (и соотв. значениях sin()) может дать существенную относительную. На мой взгляд корректней все-таки указывать именно ее.

agalakhov
05.04.2022 15:12+3В случае векторного управления моторами и во многих других можно сыграть на том, что вычислять требуется соседние значения. Но чтобы не копить ошибку, старое нельзя напрямую вводить в уравнения. Зато можно использовать его как старт для метода итераций, который в этом случае сходится очень быстро. На 32 битах не пробовал, а на AVR при работе с фиксированной точкой требовалось около 5 итераций при ~30 тактах на итерацию.

numeric Автор
07.04.2022 21:16Согласен. Вы правы применительно к задаче управления электромотором, характеризующейся регулярностью и периодичностью вычислений по принципу от достигнутого.
Представим задачу, где периодичность вырождена. Потребность вычислений возникает спонтанно, время от времени, как импульсная функция от состояния внешней среды.
Но, если такая потребность возникла, то время реакции критично.И ещё важные вводные. Погрешность измерителя, погрешность исполнителя на три порядка хуже ~|1.0|, чем погрешность вычислителя | =>0,0003 |.
В чём смысл "борьбы" за симметрию ошибки вычислителя в четвёртом порядке, если с "высот" измерителя и исполнителя таких малых порядков нет.

Razoomnick
05.04.2022 17:29+1Я никак не могу понять ситуацию с библиотечными функциями, скорость работы которых драматически зависит от величины аргумента. Это получается, что авторы библиотеки не тестировали производительность и не воспользовались очевидными свойствами симметричности и периодичности? Это ведь не экзотические функции, и это происходит в языке, которому 50 лет.
Я далёк от мира микроконтроллеров, но мне это кажется ненормальным. Может быть, этому есть логичное объяснение?

vkni
05.04.2022 18:51Имеется ввиду "величина аргумента в первой четверти". То есть при 0 < x < \pi/2. Это довольно естественно, если вы вычисляете sin(x) в цикле - чем дальше вы отстоите от 0, тем больше тактов надо сделать, чтобы придти к той же относительной точности.
Авторы библиотек тестировали производительность, но в неявных требованиях у них производительность стоит после точности. А в данном случае автор жертвует точностью.
Razoomnick
05.04.2022 21:15В том и дело, что в статье речь не о первой четверти, с первой четвертью все понятно.

И на графике, и в таблице аргументы за пределами первой четверти.

numeric Автор
05.04.2022 21:49Я никак не могу понять ситуацию с библиотечными функциями, скорость работы которых драматически зависит от величины аргумента.
Разделяю драмматизм ситуации.
Более того, тестирование библиотечных функций показывает фантастическую производительность на регулярных данных.
for ( float s, a = 0.; a < 46.; a += 15. ) { ... s = sinf( f ); ... } +============= SINF test ================== +-------------- # 1 --------------------- +-- RLS at 21:20:46 by STM32 Cortex M0 +-- CPU:32 MHz, STC[e000e014]:32000 a, sinf, clocks 0.0000, 0.0000, 1 15.0000, 0.2588, 1 30.0000, 0.5000, 1 45.0000, 0.7071, 1И картина драмматически меняется, когда регулярность нарушается слабым шумом.
for ( float s, a = 0.; a < 46.; a += 15. ) { ... s = sinf( a + noise() ); ... } +============= SINF test ================== +-------------- # 1 --------------------- +-- RLS at 21:20:46 by STM32 Cortex M0 +-- CPU:32 MHz, STC[e000e014]:32000 a, sinf, clocks 0.1900, 0.0033, 2841 15.0054, 0.2589, 2874 30.0915, 0.5014, 2874 45.0548, 0.7078, 4706
buldo
06.04.2022 04:15Тут был тег сарказм или нет?

numeric Автор
06.04.2022 08:04Тут был тег сарказм или нет?
В сообщении данные, подтверждённые многократным экспериментом.

DancingOnWater
06.04.2022 10:08+1А если забенчить вызов noise(). По идее это очень тяжелая функция

numeric Автор
06.04.2022 22:07Выше условный код, для понимания. В реальности код слегка отличается:
float rand_number( float min, float max ) { float rnd = (float) ( rand() - ( RAND_MAX / 2 ) ) / RAND_MAX; return min + rnd * ( max - min ); } #define NOISE_ON //#undef NOISE_ON void DasIstFantastish() { STimeStamp fxs, fxe; float a, b, s; int32_t t; PUT_FORMAT_MSG( "%7sf, %7s, %7s\n", "angle", "sinf", "clocks" ); for ( float f = 0.; f < 46.; f += 15. ) { #ifdef NOISE_ON b = f + rand_number(-.5, .5); #else b = f; #endif a = ( b ) * M_PI / 180.; this_moment( &fxs ); s = sinf ( a ); this_moment( &fxe ); t = this_moment_gap( &fxs, &fxe ); PUT_FORMAT_MSG( "%7.4f, %7.4f, %7ld\n", b, s, t ); } }Результат выполнения кода в зависимости от директивы NOISE_ON.
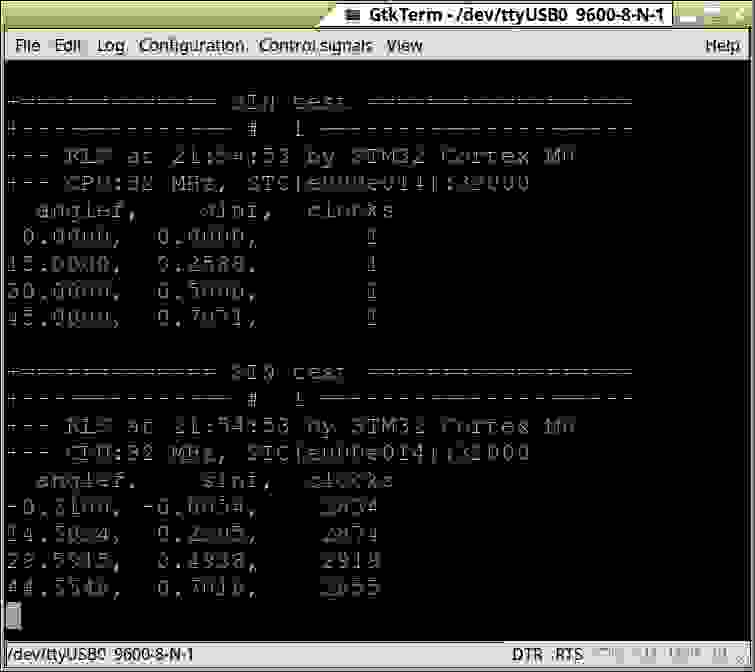

buldo
07.04.2022 04:29Так ведь в первом случае расчёты в рантайме вообще не проводятся. Компилятор вычислил значения на этапе компиляции. Тут вопрос не в регулярности данных, а в том, что всё известно на этапе компиляции.

numeric Автор
07.04.2022 07:30-1Согласен. Вы правы.
И в этом как раз засада.
Компилятор сделал то, о чём его не просили:
1. Зарезервировал (своровал) лишнюю память для вычисленных им констант;
2. Исключил вызов функции, которая теоретически может выполнять параллельную, другую работу по факту вызова;
3. Внёс искажения во временные характеристики кода в 2500(!) раз.Как Вы думаете, программисты настолько тупы, что не знают как представить известную до выполнения программы последовательность в виде массива констант? Если им это надо.
Что ещё может генерировать компилятор в обход директив программиста?
Погоня за сомнительным повышением производительности через оптимизацию двоичного кода компилятором уже приводит к тому, что программы, собранные с запретом оптимизации работаю эффективнее, чем при её наличии. К сожалению ныне надо всегда помнить об этом.
buldo
08.04.2022 03:42Компилятор делает ровно то, что вы ему сказали. У сишного/плюсового компилятора куча флагов оптимизаций. К тому же есть способы не дать компилятору оптимизировать код. Например, сделать максимальный угол не константным, а зависящим от состояния одного из пинов. Так что тут скорее вопросы не к компилятору, а к тому что вы не очень умеете в бенчмаркинг.
Как функция может выполнять другую работу? Если бы она что-то ещё делала, то компилятор не смог бы её предрасчетать. Плюс компиляторы чаще всего действуют в рамках стандарта. Стандарт не запрещает рассчитывать константы заранее. Не запрещает разворачивать циклы. Вот вы скорее всего и получили просто загрузку значения в память.
Кстати, а вы сравнивали производительность кода на разных компиляторах(не заметил, написали ли вы в статье, чем компилировали)?

numeric Автор
08.04.2022 07:21а вы сравнивали производительность кода на разных компиляторах
Могу, конечно, заблуждаться, но прикладной программист и тестировщик чужих программ - это несколько разные специальности. Это как слесарь-инструментальщик и слесарь-механик. Вроде как в одном цеху, а задачи разные. Заниматься чужим делом - сомнительный путь. (imho)
Языки программирования высокого уровня, такие как "C/C++", их стандарты созданы для снижения зависимости программиста от поставщика оборудования и средств разработки.
Соблюдение стандарта программистом - это просто установка в строчке запуска компилятора значения, определённого в технических требованиях. Например, регламент по сборке ядра линукс требует 11-й стандарт, если память не изменяет.
С другой стороны, стандарты и компиляторы делают люди, а не боги.
Людям свойственно ошибаться.
не заметил, написали ли вы в статье, чем компилировали
А внимательно-ли Вы читали статью? :-)

Geratron
05.04.2022 20:43-1Зачем это всё? А просчитать таблицу, если нужна повышенная точность - воспользоваться апроксимацией из наиболее близких значний? По-моему, бред какой-то.

numeric Автор
05.04.2022 21:01Согласен, это известный, проверенный подход.
Но, здесь суть в том, что точность требуется не повышенная, а гарантированная. И не в точках, а непрерывно с шагом 0,01 ° на всей области определения аргумента [ -5400 °.. +5400° ], применительно к бюджетным MSU с дефицитом памяти и производительности.
Где выигрыш в статических таблицах, если задача решается алгоритмически за несколько десятков слов бинарного кода?

ksbes
06.04.2022 09:35Учитывая, что всё равно всё «закатывается» в квадрант — то с такой точностью речь идёт о табличке в «жалкий» десяток-другой килобайт. Ради точности+скорости можно и пожертвовать.
Но истину тут может раскрыть только эксперимент. Да и принцип «лучшее — враг хорошего» здесь как нельзя лучше применяется. Так что смотрите сами.
Но я бы чисто из любопытства эксперимент провёл бы :)
numeric Автор
06.04.2022 21:29Проведите эксперимент! Его результат будет интересен, как минимум, всем участникам этой дискуссии.

WASD1
06.04.2022 03:42Честно говоря, у вас как-то странно смещены значения, это может выплыть боком и привести к накоплению ошибки.
Вот что дало простое суммирование по 1 градусу:
[0] : 0.000000 - 0.000000 = 0.000000
[1] : 0.017456 - 0.017452 = 0.000004
[2] : 0.034790 - 0.034899 = -0.000109
[3] : 0.052216 - 0.052336 = -0.000120
[4] : 0.069580 - 0.069756 = -0.000176
[5] : 0.086975 - 0.087156 = -0.000181
[6] : 0.104309 - 0.104528 = -0.000219
[7] : 0.121643 - 0.121869 = -0.000226
[8] : 0.138947 - 0.139173 = -0.000227
[9] : 0.156219 - 0.156434 = -0.000215
[10] : 0.173431 - 0.173648 = -0.000217
[11] : 0.190643 - 0.190809 = -0.000166
[12] : 0.207764 - 0.207912 = -0.000148
[13] : 0.224823 - 0.224951 = -0.000128
[14] : 0.241791 - 0.241922 = -0.000131
[15] : 0.258759 - 0.258819 = -0.000061
[16] : 0.275574 - 0.275637 = -0.000064
[17] : 0.292358 - 0.292372 = -0.000013
[18] : 0.308990 - 0.309017 = -0.000027
[19] : 0.325562 - 0.325568 = -0.000007
[20] : 0.342072 - 0.342020 = 0.000051
[21] : 0.358429 - 0.358368 = 0.000061
[22] : 0.374695 - 0.374607 = 0.000088
[23] : 0.390869 - 0.390731 = 0.000138
[24] : 0.406921 - 0.406737 = 0.000185
[25] : 0.422791 - 0.422618 = 0.000172
[26] : 0.438568 - 0.438371 = 0.000197
[27] : 0.454193 - 0.453991 = 0.000203
[28] : 0.469696 - 0.469472 = 0.000224
[29] : 0.485046 - 0.484810 = 0.000237
[30] : 0.500244 - 0.500000 = 0.000244
[31] : 0.515289 - 0.515038 = 0.000251
[32] : 0.530151 - 0.529919 = 0.000232
[33] : 0.544891 - 0.544639 = 0.000252
[34] : 0.559479 - 0.559193 = 0.000286
[35] : 0.573853 - 0.573576 = 0.000276
[36] : 0.588043 - 0.587785 = 0.000258
[37] : 0.602081 - 0.601815 = 0.000266
[38] : 0.615906 - 0.615661 = 0.000244
[39] : 0.629547 - 0.629320 = 0.000227
[40] : 0.642975 - 0.642788 = 0.000187
[41] : 0.656250 - 0.656059 = 0.000191
[42] : 0.669312 - 0.669131 = 0.000181
[43] : 0.682159 - 0.681998 = 0.000161
[44] : 0.694794 - 0.694658 = 0.000135
[45] : 0.707245 - 0.707107 = 0.000138
[46] : 0.719482 - 0.719340 = 0.000143
[47] : 0.731445 - 0.731354 = 0.000092
[48] : 0.743225 - 0.743145 = 0.000080
[49] : 0.754761 - 0.754710 = 0.000051
[50] : 0.766083 - 0.766044 = 0.000038
[51] : 0.777161 - 0.777146 = 0.000015
[52] : 0.787994 - 0.788011 = -0.000016
[53] : 0.798584 - 0.798636 = -0.000052
[54] : 0.808960 - 0.809017 = -0.000057
[55] : 0.819061 - 0.819152 = -0.000091
[56] : 0.828949 - 0.829038 = -0.000089
[57] : 0.838593 - 0.838671 = -0.000078
[58] : 0.847961 - 0.848048 = -0.000087
[59] : 0.857056 - 0.857167 = -0.000112
[60] : 0.865875 - 0.866025 = -0.000150
[61] : 0.874481 - 0.874620 = -0.000139
[62] : 0.882782 - 0.882948 = -0.000166
[63] : 0.890839 - 0.891007 = -0.000168
[64] : 0.898590 - 0.898794 = -0.000204
[65] : 0.906128 - 0.906308 = -0.000180
[66] : 0.913361 - 0.913545 = -0.000185
[67] : 0.920319 - 0.920505 = -0.000186
[68] : 0.927002 - 0.927184 = -0.000182
[69] : 0.933380 - 0.933580 = -0.000200
[70] : 0.939514 - 0.939693 = -0.000178
[71] : 0.945343 - 0.945519 = -0.000176
[72] : 0.950897 - 0.951057 = -0.000159
[73] : 0.956146 - 0.956305 = -0.000159
[74] : 0.961090 - 0.961262 = -0.000172
[75] : 0.965790 - 0.965926 = -0.000136
[76] : 0.970184 - 0.970296 = -0.000111
[77] : 0.974243 - 0.974370 = -0.000127
[78] : 0.978027 - 0.978148 = -0.000120
[79] : 0.981567 - 0.981627 = -0.000060
[80] : 0.984741 - 0.984808 = -0.000067
[81] : 0.987640 - 0.987688 = -0.000048
[82] : 0.990234 - 0.990268 = -0.000034
[83] : 0.992523 - 0.992546 = -0.000023
[84] : 0.994507 - 0.994522 = -0.000015
[85] : 0.996216 - 0.996195 = 0.000021
[86] : 0.997589 - 0.997564 = 0.000025
[87] : 0.998657 - 0.998630 = 0.000028
[88] : 0.999420 - 0.999391 = 0.000029
[89] : 0.999908 - 0.999848 = 0.000061
SUM = 0.000685
numeric Автор
06.04.2022 21:26Просто обнулите четвёртый и далее разряды, и снова сравните.
Этот алгоритм про результат с заданной степенью точности.
WASD1
06.04.2022 22:59Просто обнулите четвёртый и далее разряды, и снова сравните.
Не понял этот комментарий. Приведённый код не подходит к использованию "из коробки"?
> Этот алгоритм про результат с заданной степенью точности.
Но ошибка распределена очень неравномерно.

Refridgerator
06.04.2022 06:04+1Синус с точностью до 3-х знаков после запятой аппроксимируется многочленом 5-ой степени:
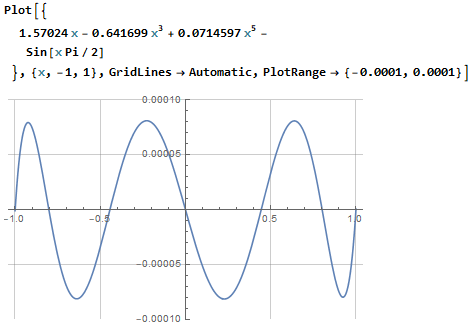
Я так и не смог понять, к чему все эти сложности со сплайнами.
numeric Автор
06.04.2022 07:31Сплайн - это просто форма. Это форма представления многочлена, оптимизированная для компьютера.
(imho)

Refridgerator
08.04.2022 05:33Нет, сплайн — это инструмент интерполяции, в то время как вы решаете задачу аппроксимации. В интерполяции коэффициенты (например) кубического многочлена считаются исходя из граничных условий — значения в крайних точках и их производные, чтобы обеспечить гладкую стыковку. В аппроксимации более важно максимальное или среднеквадратичное отклонение одной функции от другой, соответственно и коэффициенты считаются по другим методикам. Кроме того для синусоиды имеют значение и другие факторы — уровень гармоник и постоянной составляющей, которые вы через сплайны Безье минимизировать никак не сможете.

Firelander
07.04.2022 18:32Что насчет CORDIC? Это по-моему вполне себе стандарт быстрого вычисления тригонометрии на микроконтроллерах. Вроде бы даже в DSP либе есть его быстрая реализация с использованием специальных команд процессора.

numeric Автор
07.04.2022 20:10Есть сомнения, что CORDIC даст какие-либо преимущества на бюджетных MCU.






Rsa97
А с формулой Бхаскара не сравнивали? Точность у неё похуже, |0.0016|, но сама формула очень простая.
numeric Автор
Согласен, формула простая и красивая.
Не сравнивал.
С первого взгляда, подпрограмма на её основе должна работать быстрее.
С другой стороны:
- хотелось получить три точных знака, получаемые простым отбрасыванием лишних разрядов, без округления;
- изложенный метод позволяет получить больше точных знака через отбрасывание лишних разрядов без потери производительности, но с расходом памяти под статические данные;
- вероятная перспектива других тригонометрических функций диктует единообразие применяемого мат. аппарата.
mobi
Там ведь деление используется?
Rsa97
Да, но в приведённом алгоритме оно тоже используется.
mobi
Я вижу только деления на константы, что компилятор сведет к умножению.
numeric Автор
Мы понимаем, что деление, это самая медленная операция из простых арифметических.
Однако, вопрос в другом.
Гарантированная точность в 3-м и далее знаках после десятичной запятой, получаемая простым отбрасыванием лишних разрядов без лишних затрат на округление.