Вместо вступления
Прежде всего хочется выразить признательность всем, кто откликнулся на первую статью об оптимизации кода на языке C/C++ на примере функции для вычисления квадратного корня из целого с округлением до ближайшего целого. Благодаря экспертному вниманию была исправлена опечатка в тексте; копилка эффективных алгоритмов пополнилась.
Интересен алгоритм sqrxi32 от @Sdima1357 — Пример 1, далее для краткости именуемый как «_i32». Алгоритм «_i32» безусловно выполняет главное условие задачи — «округление до ближайшего целого» — на всём множестве значений аргумента [ 0 .. 0xFFFFFFFF ], при этом показывает высокую производительность.
Пример 1: Квадратный корень из целого с округлением до ближайшего целого — «_i32».
uint16_t sqrxi32( uint32_t y )
{
if ( y == 1 )
return 1;
uint32_t xh = y > 0x10000ul ? 0x10000ul : y;
uint32_t xl = 0;
uint32_t xc;
for ( int k = 0; k < 16; k++ )
{
xc = ( xh + xl ) >> 1ul;
if ( xc * xc - xc >= y )
{
xh = xc;
}
else
{
xl = xc;
}
}
return ( xh + xl ) >> 1ul;
}Другое хорошее качество алгоритма «_i32» — предсказуемость по времени. Время работы «_i32» постоянно в отличие от алгоритма «_evn», потребляющего машинное время пропорционально модулю аргумента.
О чём этот текст
Наблюдение комплексного влияния параметров сборки и целевой аппаратной платформы на итоговую производительность, применительно к одному и тому же исходному коду.
Исходный код содержит решение одной задачи разными алгоритмами.
Анализ результатов наблюдений за рамками настоящей публикации.
Условия и допуски
Для сокращение текста принимаем:
аппаратных платформ для тестов — 3 платформы;
вариантов оптимизации сборки — 3 значения
Для сборки двоичного кода применяем:
Одну единицу компиляции теста (файл main.c)
Компиляцию в моно-поточный исполняемый файл
Единую сборочную среду: CubeIDE (она же Eclipce CDT)
Стандартные настройки профиля сборки RELEASE в среде CubeIDE
Единый диалект компилятора: «ISO C11 + gnu extensions» (-std=gnu11)
-
Применительно к микроконтроллерам:
CubeMX — default settings, +48MHz, +USART1, +HAL;
Runtime lib: Reduced C ( --spec=nano.specs );
Use float with printf from new lib nano ( -u _printf_float );
Таблица 1: Варианты сборки исполняемого кода

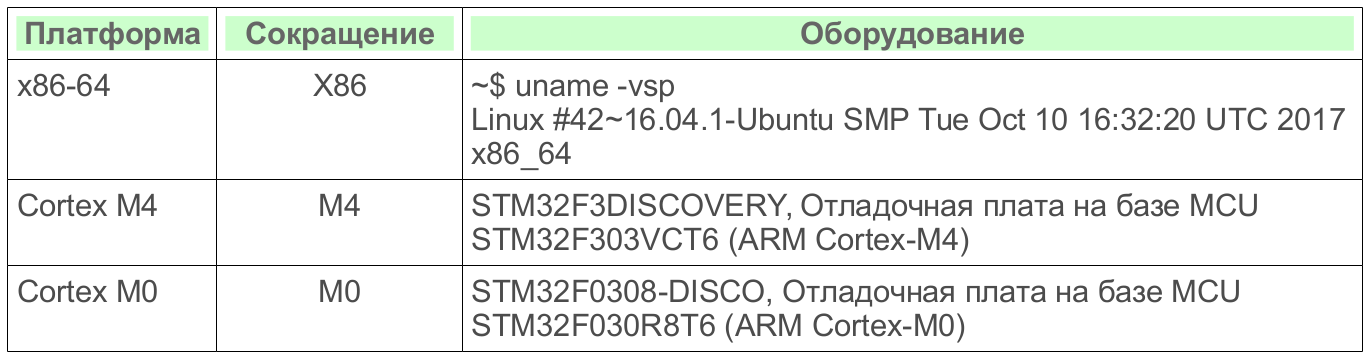
Таблица 2: Общие характеристики аппаратных платформ

Таблица 3: Технические характеристики аппаратных платформ
Тестовый набор содержит некоторые алгоритмы из предыдущей статьи и комментариев к ней.
Для оценки FPU платформы «M4» в тестовый набор добавлена функция sqrt_fps, решающая вычислительную задачу с применением коротких действительных (float), именуемая далее «_fps» (Float Point Short) — Пример 2.
Пример 2: Квадратный корень из целого с точностью float — «_fps»
uint16_t sqrt_fps( uint32_t number )
{
if ( number < 2 )
return (uint16_t) number;
float f_rslt = sqrtf( number );
uint32_t rslt = (uint32_t) f_rslt;
if ( !( f_rslt - (float) rslt < .5 ) )
rslt++;
return (uint16_t) rslt;
}Функция «_fps» работает без ошибок с аргументом менее 22-х бит, что соответствует десятичному порядку 1E+5 — Иллюстрация 1.
Иллюстрация 1: Ошибки функции "_fps" на порядках 1E+6+

Для всех наблюдаемых алгоритмов ограничиваем диапазон аргумента множеством значений
[0 .. 1E+5].
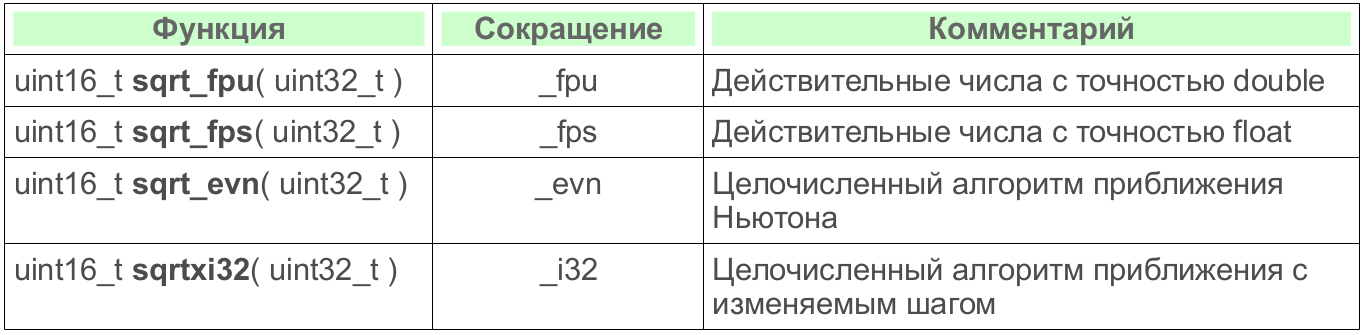
Таблица 4: Список наблюдаемых алгоритмов
Основная единица измерения — производительность, среднее число циклических вызовов функции за одну миллисекунду.
Относительная производительность платформ
Ожидаемо, производительность платформы «x86» выше производительности платформы «ARM Cortex» безотносительно характера оптимизации сборки. Последнее демонстрирует левая часть графика — Иллюстрация 2.
Иллюстрация 2: Относительная производительность аппаратных платформ
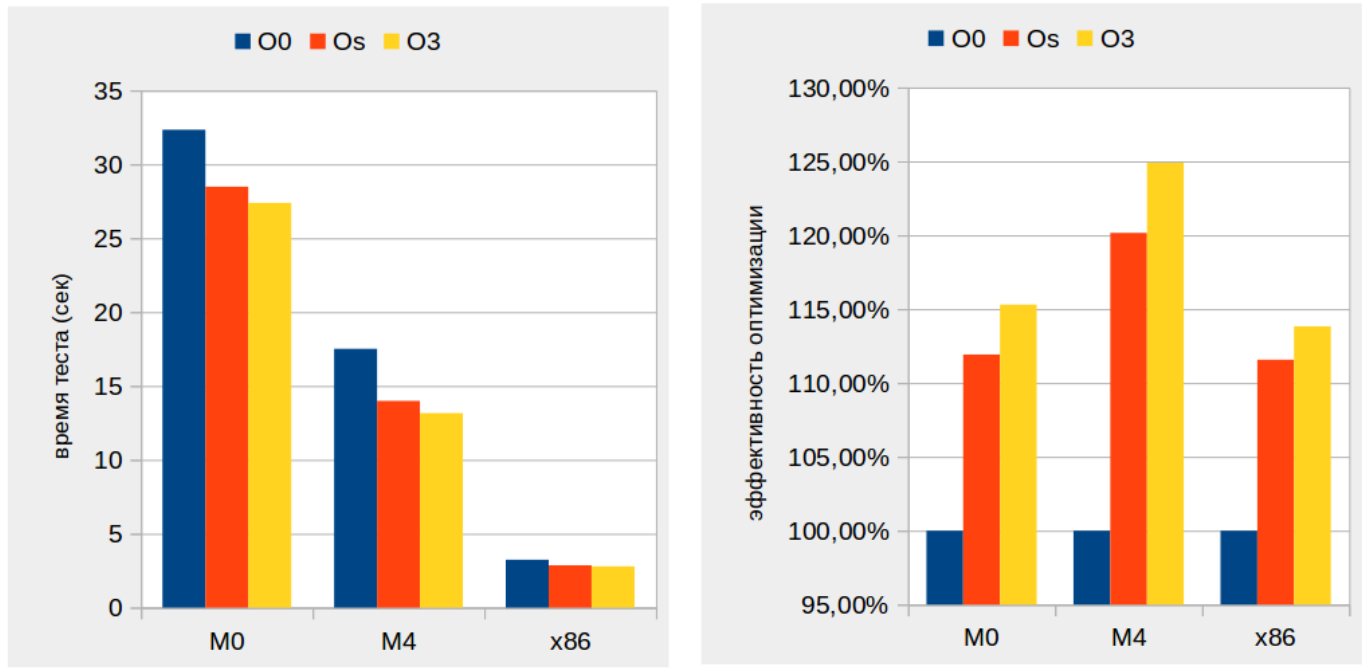
На левой части графика по оси Y отображается среднее время последовательного выполнения всех тестов (Таблица 4), измеренное в секундах. На оси X — аппаратные платформы.
Чем ниже высота столбика на левой части графика (Иллюстрация 2), тем выше скорость работы, тем лучше производительность соответствующей аппаратной платформы.
График каждой платформы, в свою очередь, представлен тремя столбцами, демонстрирующими зависимость производительности от варианта оптимизации сборки: -O0, -Os, -O3.
Правая часть графика (Иллюстрация 2) показывает относительный прирост производительности у каждой аппаратной платформы в зависимости от варианта оптимизации сборки: -O0, -Os, -O3.
Производительность 100% демонстрирует двоичный код, собранный без оптимизации ( -O0 ). Это базовая производительность платформы.
Чем выше высота столбика относительно базовой производительности ( ‑O0 ) в правой части графика, тем лучше оптимизационные возможности программно-аппаратной платформы.
Наблюдаем наибольший прирост производительности от оптимизации на этапе сборки на платформе «M4».
Платформа x86
На графике (Иллюстрация 3) по оси Y отображается число цикличных вызовов наблюдаемых функций за одну миллисекунду. На оси X — наблюдаемые функции (Таблица 4).
Чем выше на графике столбики, тем лучше производительность.
Цветом на оси X обозначен способ оптимизации на этапе сборки. Соответствие цвета и характера оптимизации отражает легенда.
Иллюстрация 3: Производительность алгоритмов на платформе x86

Платформа «x86» максимально раскрывает преимущества алгоритмов с плавающей точкой перед целочисленными.
Заслуживает отдельного внимания часть графика в оранжевом контуре.
Производительность кода без оптимизации ( ‑O0 ) лучше на 39% для алгоритма «_fpu» ( ‑Os ) и на 16% для алгоритма «_fps» ( ‑O3 ). Другими словами, любая оптимизация на этапе сборки снижает производительность платформы «x86» на действительных числах.
В то же время, целочисленные алгоритмы показывают ожидаемый прирост производительности при сборке с параметрами -O3 и -Os.
Платформа M4
Платформа «M4» демонстрирует предсказуемый результат (Иллюстрация 4).
Иллюстрация 4: Производительность алгоритмов на платформе M4

Модуль с плавающей точкой «M4» даёт ожидаемый прирост производительности для алгоритма «_fps», основанного на коротком действительном — float.
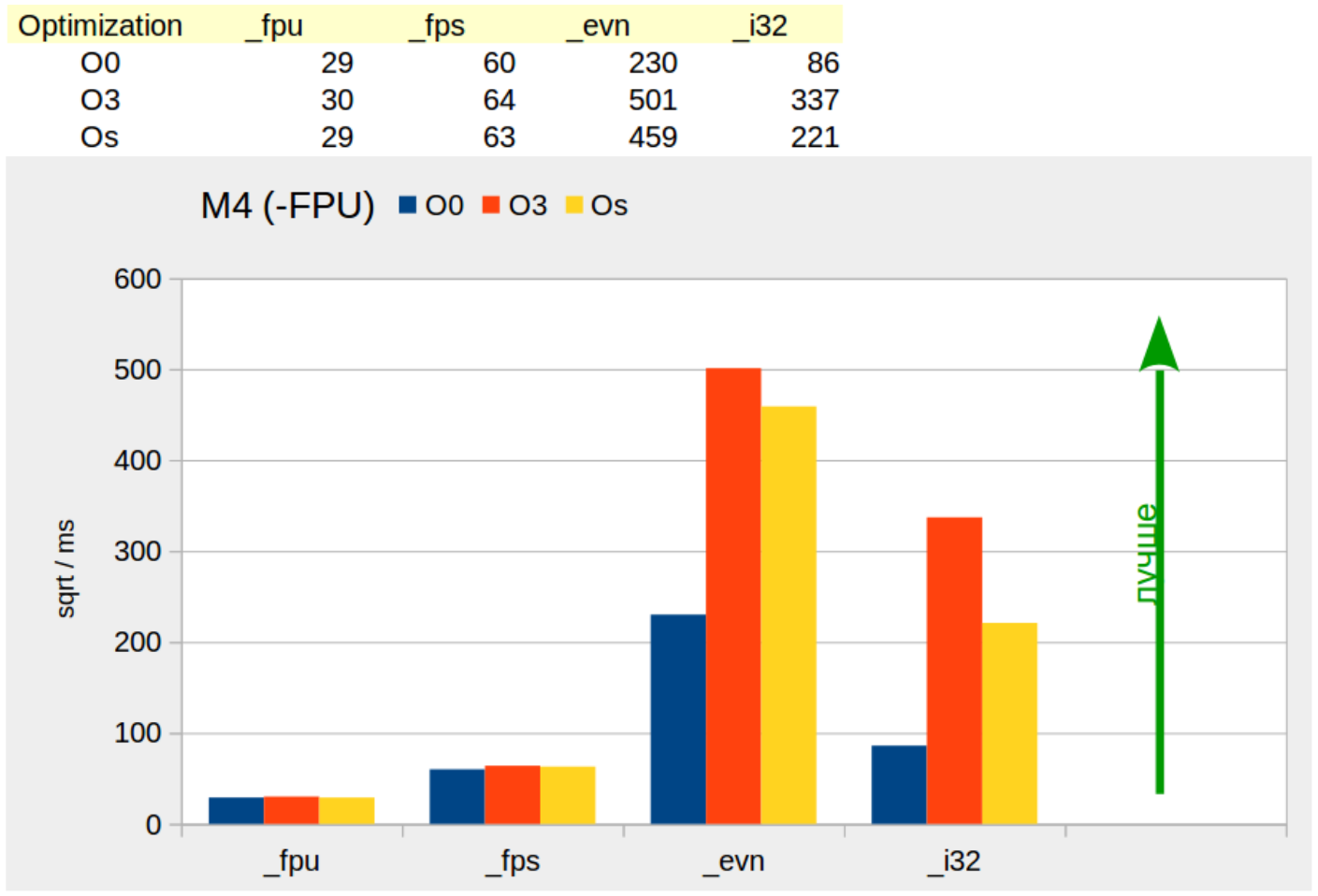
Последнее подтверждается результатом сравнения производительности алгоритмов при отключенном модуле FPU на платформе «M4» — Иллюстрация 5.
Наблюдая графики помним, что точность вычислений алгоритма «_fps» гарантируется в диапазоном 1E+5 (см. Иллюстрация 1) без относительно того, включен ли модуль FPU на «M4» или нет.
Иллюстрация 5: Производительность алгоритмов на платформе M4 без FPU
Платформа M0
Результаты платформы «M0» похожи на результаты платформы «M4» без FPU (Иллюстрация 5), только медленнее — Иллюстрация 6.
Заметим, тактовая частота при тестировании устанавливалась одинаковой и для «M4», и для «M0» — 48 MHz. Однако, производительность «M0» хуже в два с лишним раза, чем «M4», в условиях равенства прочих характеристик.
Иллюстрация 6: Производительность алгоритмов на платформе M0
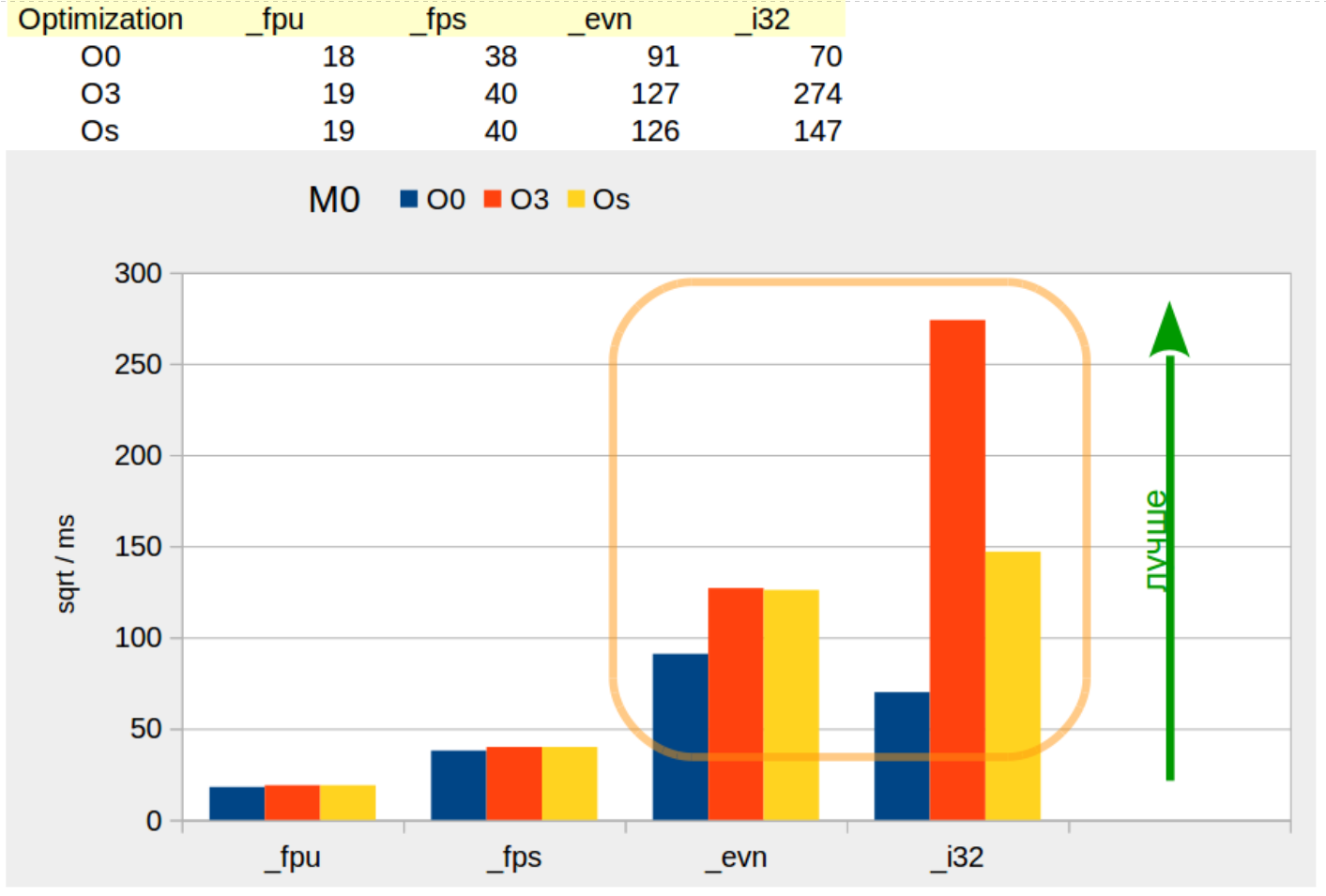
Алгоритм «_fps» на платформе «M0» ожидаемо опережает в два раза алгоритм «_fpu».
Целочисленные алгоритмы опережают алгоритмы с плавающей точкой.
По странному стечению обстоятельств в заключительном графике (Иллюстрация 6) снова есть место для оранжевого контура.
При сборке без оптимизации ( ‑O0 ) алгоритм «_evn» быстрее алгоритма «_i32». И алгоритм «_evn» медленнее, чем «_i32», если сборка проводится с оптимизацией.
Снова наблюдается относительное снижение производительности от оптимизации на этапе сборки. Заметим, у целочисленных алгоритмов на платформах «M4» и «x86» подобного эффекта нет.
Вместо заключения
Производительность программы зависит от многих причин.
Оптимизация на этапе сборки способна ухудшать производительность, замедлять программу, что демонстрируют экспериментальные данные в оранжевых контурах выше (Иллюстрация 3 и Иллюстрация 6).
Цена аппаратной платформы безусловно повышает производительность программы безотносительно качества исходного кода и эффективности компилятора.
Общего правила, как создавать эффективные программы, нет. Задача оптимизации и профилирования решается индивидуально в каждом конкретном случае.
Приложение 1. Порядок тестирования платформы x86
Создать в среде CubeIDE (Eclipse CDT) проект C штатным способом
Написать текст программы — Пример 3
Добавить в проект файл sqrt_cmp.h — Пример 6
-
Осуществить сборку и запуск программы:
штатными средствами IDE;
или из командной строки — Пример 4
Меняя вид оптимизации ( -O0, -O3, -Os ) наблюдать результат.
Пример 3: Исходный текст программы x86 — main.c
#include "sqrt_cmp.h"
int main( void )
{
main_Of_SqrtComp();
return 0;
}
Пример 4 Запуск теста на платформе x86 из терминала
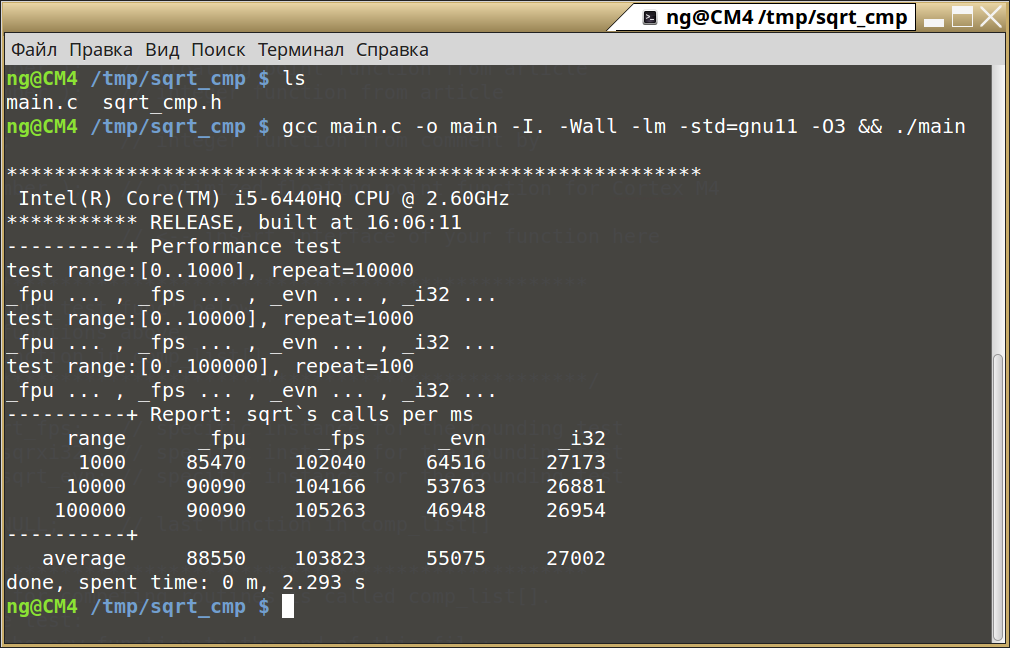
gcc main.c -o main -I. -Wall -lm -std=gnu11 -O3 && ./mainЗапуск теста из терминала платформы «x86» предполагает, что файлы main.c и sqrt_cmp.h располагаются в одном каталоге, и этот каталог выбран рабочим (pwd).
Иллюстрация 7: Запуск теста из терминала «x86»
Приложение 2. Порядок тестирования платформы STM32
Создать в среде CubeIDE проект STM32 штатным способом (CubeMX)
Добавить файл sqrt_cmp.h в проект STM32 — Пример 6
Включить sqrt_cmp.h в файл main.c — Пример 5
Осуществить сборку и запуск программы штатными средствами IDE
Меняя вид оптимизации ( -O0, -O3, -Os ) наблюдать результат
Пример 5: Исходный текст для STM32 (с пропусками < ... >) — main.c
< … >
/* Private includes ----------------------------------------------------------*/
/* USER CODE BEGIN Includes */
#include "sqrt_cmp.h"
/* USER CODE END Includes */
< … >
/**
* @brief The application entry point.
* @retval int
*/
int main(void)
{
< … >
/* Infinite loop */
/* USER CODE BEGIN WHILE */
main_Of_SqrtComp();
while (1)
{
/* USER CODE END WHILE */
/* USER CODE BEGIN 3 */
}
/* USER CODE END 3 */
Приложение 3. Порядок тестирования других алгоритмов и платформ
Сборка теста для других платформ проводится по аналогии.
Для отличных от упомянутых выше аппаратных платформ (Таблица 3), вероятно, потребуется косметическая модификация файла «sqrt_cmp.h».
Пример 6: Содержание файла sqrt_cmp.h
/******************************************************************************
* File: sqrt_cmp.h Created on 5 авг. 2020 г.
* CC0 1.0 Universal (CC0 1.0)
* Creative Commons Public Domain Dedication
* No Copyright
*
* TAB Size .EQ 4
********************************************************************************/
#ifndef __SQRT_CMP_H
#define __SQRT_CMP_H
#include <math.h>
#include <stdio.h>
#include <stdint.h>
#ifdef __cplusplus
extern "C" {
#endif
/******************************************************************************
* Interface of the entry point for all sqrt tests
******************************************************************************/
void main_Of_SqrtComp();
/******************************************************************************
* test case selection: TEST_SET
* select one of the test suite via a comment.
******************************************************************************/
#define TEST_SET TEST_ALL
//#define TEST_SET TEST_ROUNDING
//#define TEST_SET TEST_PERFORMANCE
/******************************************************************************
* Interfaces of test functions.
* See implementation of them at the end of this file.
******************************************************************************/
typedef uint16_t (*sqrt_func)( uint32_t number );
uint16_t sqrt_fpu( uint32_t number ); // floating point function from article
uint16_t sqrt_evn( uint32_t number ); // integer function from article
uint16_t sqrxi32( uint32_t y ); // integer function from comment by
uint16_t sqrt_fps( uint32_t number ); // optimized floating point function for Cortex M4
// <-- insert interface of your function here
/******************************************************************************
* Set to variable named as 'round_test_func' below
* to the alias of one of the functions above.
* The NULL will select last function in comp_list[]
******************************************************************************/
sqrt_func round_test_func = sqrt_fps; // specific instance for the rounding test
//sqrt_func round_test_func = sqrxi32; // specific instance for the rounding test
//sqrt_func round_test_func = sqrt_evn; // specific instance for the rounding test
//sqrt_func round_test_func = NULL; // last function in comp_list[]
/******************************************************************************
* The array of test functions for competing routines is called comp_list[].
* Adding a new function to the test:
- copy the implementation of the new function to the end of this file;
- declare the function interface at the beginning of this file;
- add the alias and declaration of the new function to
end of array named comp_list[].
******************************************************************************/
// @formatter:off
typedef struct
{
sqrt_func fsqrt;
char * alias;
} SCompFunc;
SCompFunc comp_list[] = // competition list
{
{ sqrt_fpu, "_fpu" },
{ sqrt_fps, "_fps" },
{ sqrt_evn, "_evn" },
{ sqrxi32, "_i32" }
// <-- insert your function name & alias here
};
/* @formatter:on */
/******************************************************************************
* Platform-independent definitions
******************************************************************************/
#define PUT_FORMAT_MSG(f_, ...) { \
sprintf( (char *)s_buf, (char *)f_, ##__VA_ARGS__ ); \
PUT_MSG( (char *)s_buf ); }
#define MS_PER_SEC 1000
#define US_PER_SEC ( MS_PER_SEC * MS_PER_SEC )
#define ARRAY_SIZE(a) (sizeof a / sizeof *a) // size of static array at runtime
#define SIRV(f) if ( f ) ; // suppress Ignore Return Value warning
/******************************************************************************
* Platform-specific defines
******************************************************************************/
#if defined( USE_HAL_DRIVER ) // STM32 ARM Cortex platform
# include <string.h>
# include "main.h"
//*****************************************************************************
// Platform-specific defines for the helper functions
# define SCALE_RATE 1 // must be .GE than 1
# define X_CLOCK HAL_GetTick()
# define X_DELAY( ms ) HAL_Delay( ms )
//*****************************************************************************
// Platform-specific defines for the terminal output
# define USART_HANDLE huart1 // set valid USART handler alias here defined by the config of MCU
# define USART_TIMEOUT 150 // max timeout for HAL_UART_Transmit
extern UART_HandleTypeDef USART_HANDLE;
extern HAL_StatusTypeDef HAL_UART_Transmit ( UART_HandleTypeDef *huart, uint8_t *pData, uint16_t Size, uint32_t Timeout );
# define PUT_MSG( msg ) \
HAL_UART_Transmit( &USART_HANDLE, (uint8_t *)msg, strlen( (char *)msg ), USART_TIMEOUT )
# define CPU_CLOCK_MHz ( SystemCoreClock / US_PER_SEC ) // CPU CLK in MHz
# if defined( STM32F0 )
# define CPU_ID ( "STM32 ARM Cortex M0" )
# elif defined ( STM32F3 )
# define CPU_ID ( "STM32 ARM Cortex M4" )
# else
# define CPU_ID ( "Maybe STM32 ARM Cortex" )
# endif
# define PUT_SYS_INFO PUT_FORMAT_MSG( " %s @ "fdU()" MHz\n", CPU_ID, CPU_CLOCK_MHz )
#else // #if defined( USE_HAL_DRIVER )
# include <time.h>
# include <stdlib.h>
//*****************************************************************************
// Platform-specific defines for the helper functions
# define SCALE_RATE 100 // must be .GE than 1
# define X_CLOCK (uint32_t) x_clock()
# define X_DELAY( ms ) x_delay( ms )
uint32_t x_clock()
{
uint64_t result = (uint64_t) clock();
result *= MS_PER_SEC;
result /= CLOCKS_PER_SEC;
return (uint32_t) result;
}
void x_delay( uint32_t ms )
{
uint64_t tm = x_clock();
while ( ( x_clock() - tm ) < ms )
;
}
//*****************************************************************************
// Platform-specific defines for the terminal output
# define PUT_MSG( msg ) \
printf( "%s", (char *)msg ), fflush ( stdout )
# if defined( __unix__ ) // anybody other platform for gcc
# define PUT_SYS_INFO SIRV( system( "cat /proc/cpuinfo | grep 'model name' | head -1 | sed s/'model name\t:'/''/" ) )
# else
# define PUT_SYS_INFO PUT_MSG( "Undefined System & CPU" )
# endif // # if defined( __unix__ ) // anybody other platform for gcc
#endif // #if defined( USE_HAL_DRIVER )
#if ( __WORDSIZE == 64 )
# define fdI(s) "%" #s "d"
# define fdU(s) "%" #s "u"
# define fdX(s) "%" #s "x"
#else // let's say __WORDSIZE == 32
# define fdI(s) "%" #s "ld"
# define fdU(s) "%" #s "lu"
# define fdX(s) "%" #s "lx"
#endif // #if ( __WORDSIZE == 64 )
#if defined ( DEBUG ) || defined ( _DEBUG ) // chk build mode of CubeIDE
# define BUILD_MODE "DEBUG"
#else // Maybe Release
# define BUILD_MODE "RELEASE"
#endif // #if defined ( DEBUG ) || defined ( _DEBUG )
/******************************************************************************
* the helper data with testing ranges
******************************************************************************/
// @formatter:off
typedef struct
{
uint32_t start;
uint32_t stop;
uint32_t repeat;
} STestRange;
STestRange test_rngs[] =
{
{ 0, 1000, 100 * SCALE_RATE },
{ 0, 10000, 10 * SCALE_RATE },
{ 0, 100000, 1 * SCALE_RATE }
};
uint32_t test_results[ARRAY_SIZE( test_rngs )][ARRAY_SIZE( comp_list ) + 1];
#define MSG_BUFF_SIZE 512
uint8_t s_buf[MSG_BUFF_SIZE]; // buffer for a terminal output
/* @formatter:on */
/******************************************************************************
* Test sets definitions. Do not change it.
******************************************************************************/
#define TEST_ROUNDING 1
#define TEST_PERFORMANCE 2
#define TEST_ALL ( TEST_ROUNDING | TEST_PERFORMANCE )
#ifndef TEST_SET
# define TEST_SET TEST_ALL
#endif
#define HI_ROUND_TEST_RANGE_END 0x007FFFFFUL
#define HI_ROUND_TEST_RANGE_START ( HI_ROUND_TEST_RANGE_END >> 4 )
/******************************************************************************
* Interface of helper functions
******************************************************************************/
void main_Header();
void testRounding();
void testPerformance();
/******************************************************************************
* Implementation of the entry point for all sqrt tests
******************************************************************************/
void main_Of_SqrtComp()
{
X_DELAY( MS_PER_SEC / 2 ); // suppress the output of a previous instance
// while the new instance is loading into the MCU
uint32_t start_time = X_CLOCK;
main_Header();
// checking normal and extended ranges for rounding
if ( TEST_SET & TEST_ROUNDING )
testRounding();
// checking normal ranges on execution time
if ( TEST_SET & TEST_PERFORMANCE )
testPerformance();
uint32_t test_time = X_CLOCK - start_time;
uint32_t test_m = ( test_time / MS_PER_SEC ) / 60;
uint32_t test_s = ( test_time / MS_PER_SEC ) % 60;
uint32_t test_ms = test_time % MS_PER_SEC;
PUT_FORMAT_MSG( "\ndone, spent time: "fdU()" m, "fdU()"."fdU()" s\n", test_m, test_s, test_ms );
}
/******************************************************************************
* Implementation of the helper functions
******************************************************************************/
void main_Header()
{
PUT_MSG( "\n\n**********************************************************\n" );
PUT_SYS_INFO;
PUT_FORMAT_MSG( "*********** %s, built at %s\n", BUILD_MODE, __TIME__ );
}
void testPerformance()
{
uint32_t i_func, i_rpt, i_rng;
uint32_t number, first, second, diff;
uint64_t temp;
PUT_MSG( "----------+ Performance test" );
for ( i_rng = 0; i_rng < ARRAY_SIZE( test_rngs ); i_rng++ )
{
PUT_MSG( "\n" );
PUT_FORMAT_MSG( "test range:["fdU()".."fdU()"], repeat="fdU()"\n", test_rngs[i_rng].start, test_rngs[i_rng].stop,
test_rngs[i_rng].repeat );
test_results[i_rng][0] = test_rngs[i_rng].stop;
for ( i_func = 0; i_func < ARRAY_SIZE( comp_list ); i_func++ )
{
PUT_FORMAT_MSG( "%s ... ", comp_list[i_func].alias );
first = X_CLOCK;
for ( i_rpt = 0; i_rpt < test_rngs[i_rng].repeat; i_rpt++ )
for ( number = test_rngs[i_rng].start; number < test_rngs[i_rng].stop; number++ )
comp_list[i_func].fsqrt( number );
second = X_CLOCK;
diff = second - first;
temp = ( test_rngs[i_rng].stop - test_rngs[i_rng].start ) * test_rngs[i_rng].repeat;
test_results[i_rng][i_func + 1] = (uint32_t) ( temp / diff );
if ( i_func < ARRAY_SIZE( comp_list ) - 1 )
PUT_MSG( ", " );
}
}
// small report
PUT_FORMAT_MSG( "\n----------+ Report: sqrt`s calls per ms\n%10s", "range" );
for ( i_func = 0; i_func < ARRAY_SIZE( comp_list ); i_func++ )
PUT_FORMAT_MSG( "%10s", comp_list[i_func].alias );
for ( i_rng = 0; i_rng < ARRAY_SIZE( test_rngs ); i_rng++ )
{
PUT_MSG( "\n" );
for ( i_func = 0; i_func < ARRAY_SIZE( comp_list ) + 1; i_func++ )
PUT_FORMAT_MSG( fdU( 10 ), test_results[i_rng][i_func] );
}
PUT_FORMAT_MSG( "\n----------+\n%10s", "average" );
for ( i_func = 0; i_func < ARRAY_SIZE( comp_list ); i_func++ )
{
temp = 0;
for ( i_rng = 0; i_rng < ARRAY_SIZE( test_rngs ); i_rng++ )
temp += test_results[i_rng][i_func + 1];
temp /= ARRAY_SIZE( test_rngs );
PUT_FORMAT_MSG( fdU( 10 ), (uint32_t)temp );
}
}
void testRoundingFunction( uint32_t start, uint32_t finish, sqrt_func psqrt, char *fname );
void testRounding()
{
uint16_t i_rng;
uint16_t f_rng;
PUT_MSG( "----------+ Rounding test\n" );
// checking the existence for the test function
for ( f_rng = 0; f_rng < ARRAY_SIZE( comp_list ); f_rng++ )
if ( comp_list[f_rng].fsqrt == round_test_func )
break;
if ( !( f_rng < ARRAY_SIZE( comp_list ) ) )
{
f_rng = ARRAY_SIZE( comp_list ) - 1;
PUT_FORMAT_MSG( "Value of 'round_test_func' not found.\n" );
}
PUT_FORMAT_MSG( "Function '%s' is tested for rounding.\n", comp_list[f_rng].alias );
// checking standard ranges
for ( i_rng = 0; i_rng < ARRAY_SIZE( test_rngs ); i_rng++ )
testRoundingFunction( test_rngs[i_rng].start, test_rngs[i_rng].stop, comp_list[f_rng].fsqrt, comp_list[f_rng].alias );
// checking extended range
testRoundingFunction( HI_ROUND_TEST_RANGE_START, HI_ROUND_TEST_RANGE_END, comp_list[f_rng].fsqrt, comp_list[f_rng].alias );
}
void turn_the_fan( uint32_t ms );
void testRoundingFunction( uint32_t start, uint32_t finish, sqrt_func psqrt, char *fname )
{
uint32_t rf, ri;
uint32_t n, c = 0;
PUT_FORMAT_MSG( "test range:["fdU( 10 )".."fdU( 10 )"] ... ", start, finish );
for ( n = start; n < finish; n++ )
{
rf = sqrt_fpu( n );
ri = ( *psqrt )( n );
if ( rf != ri )
{
if ( c++ > 3 )
{
PUT_FORMAT_MSG( "\b\n(!)too many mistakes in '%s', ", fname );
break;
}
else
{
double d = sqrt( (double) n );
PUT_FORMAT_MSG( "\b\n%s("fdU( 10 )")="fdU()" != "fdU(), fname, n, ri, rf );
PUT_FORMAT_MSG( " (real value is %.6lf)", d );
}
}
turn_the_fan( MS_PER_SEC );
}
if ( !c )
{
PUT_FORMAT_MSG( "\b done.\n" );
}
else
{
PUT_FORMAT_MSG( "test failed.\n" );
}
}
void turn_the_fan( uint32_t ms )
{
static char ca[] = "|/-\\";
static uint32_t cs = ARRAY_SIZE(ca) - 1;
static uint32_t cn = 0;
static uint32_t at = 0;
uint32_t ct = X_CLOCK;
if ( ct - at > ms )
{
at = ct;
PUT_FORMAT_MSG( "\b%c", ca[cn++ % cs] );
}
}
/******************************************************************************
* Implementation of the sqrt functions
******************************************************************************/
// floating point arg & result with double
uint16_t sqrt_fpu( uint32_t number )
{
if ( number < 2 )
return (uint16_t) number;
double f_rslt = sqrt( number );
uint32_t rslt = (uint32_t) f_rslt;
if ( !( f_rslt - (double) rslt < .5 ) )
rslt++;
return (uint16_t) rslt;
}
// floating point arg & result with float
uint16_t sqrt_fps( uint32_t number )
{
if ( number < 2 )
return (uint16_t) number;
float f_rslt = sqrtf( number );
uint32_t rslt = (uint32_t) f_rslt;
if ( !( f_rslt - (float) rslt < .5 ) )
rslt++;
return (uint16_t) rslt;
}
// unsigned integer arg & result
// @formatter:off
uint16_t sqrt_evn ( uint32_t number )
{
if ( number < 2 )
return ( uint16_t ) number;
uint32_t temp;
uint32_t div;
uint32_t rslt;
if ( number & 0xFFFF0000L )
if ( number & 0xFF000000L )
if ( number & 0xF0000000L )
if ( number & 0xE0000000L )
div = 43771;
else
div = 22250;
else
if ( number & 0x0C000000L )
div = 11310;
else
div = 5749;
else
if ( number & 0x00F00000L )
if ( number & 0x00C00000L )
div = 2923;
else
div = 1486;
else
if ( number & 0x000C0000L )
div = 755;
else
div = 384;
else
if ( number & 0xFF00L )
if ( number & 0xF000L )
if ( number & 0xC000L )
div = 195;
else
div = 99;
else
if ( number & 0x0C00L )
div = 50;
else
div = 25;
else
if ( number & 0xF0L )
if ( number & 0x80L )
div = 13;
else
div = 7;
else
div = 3;
rslt = number;
while ( 1 )
{
temp = number / div;
temp += div;
div = temp >> 1;
div += temp & 1;
if ( rslt > div )
rslt = div;
else
{
if ( number / rslt == rslt - 1 && number % rslt == 0 )
rslt--;
return ( uint16_t ) rslt;
}
}
}
/* @formatter:on */
// unsigned integer arg & result
uint16_t sqrxi32( uint32_t y )
{
if ( y == 1 )
return 1;
uint32_t xh = y > 0x10000ul ? 0x10000ul : y;
uint32_t xl = 0;
uint32_t xc;
for ( int k = 0; k < 16; k++ )
{
xc = ( xh + xl ) >> 1ul;
if ( xc * xc - xc >= y )
{
xh = xc;
}
else
{
xl = xc;
}
}
return ( xh + xl ) >> 1ul;
}
// <-- insert implementation of your function sqrt here
#ifdef __cplusplus
}
#endif
#endif // __SQRT_CMP_H

