«Только две вещи бесконечны - Вселенная и человеческая глупость, хотя насчёт Вселенной я не уверен». (Альберт Эйнштейн)
Задача коммивояжёра – одна из интереснейших подзадач комбинаторной оптимизации. Впервые мне пришлось с ней столкнуться, работая над логистической системой торгового предприятия.
Типичный маршрут доставки товара предприятия состоял из пары десятков точек, изредка доходящий до 25-26. Матрица расстояний рассчитывалась с помощью алгоритма Дейкстры. Дальше нужно было выбрать оптимальный маршрут из возможных.
Решение методом грубой силы не подходило из-за вычислительной сложности. Была предпринята попытка реализовать метод ветвления и границ с отсечением в глубину. В целом, подход себя оправдывал, но иногда при некоторых специфических входных данных алгоритм выдавал решение далёкое от оптимального.
Хотя обычному человеку достаточно сложно построить оптимальный маршрут на десятках точек, но он легко зрительно замечает, если граф не планарен при его визуализации в виде пути на карте.
Так было и в тот раз, шеф сказал: - Это вообще никуда не годится. Мне нужно только точное решение, точное и ни как иначе!

Собственно, мне известны только три метода нахождения точного решения:
Перебор грубой силой (brute force).
Ветвления и границ с полным перебором.
Динамическое программирование.
Изначально все тексты были реализованы на Pascal. Но так как современные разработчики достаточно прохладно относится к данному архаичному языку, я конвертировал тексты на Python. Этот более современный язык, невероятно удобен и дружествен к программисту, но и скорость работы программ на нём сильно уступает, о чём я добавлю пару слов ниже.
1. Метод грубой силы
Мне часто встречалась мысль о том, что при полном переборе поиск оптимального маршрута можно ждать веками.
Поскольку коммивояжёр в каждом из городов встает перед выбором следующего города из тех, что он ещё не посетил, существует (n-1)! маршрутов для асимметричной и (n-1)!/2 маршрутов для симметричной задачи коммивояжёра.
Прикинем на глаз, для 26 городов в симметричном варианте как верхний предел.
Получаем 25!/2 = 7755605021665492992000000 маршрутов.
Даже если проверять по миллиарду маршрутов в секунду, то солнце потухнет раньше, чем мы дождёмся результата.
Если у Вас остались сомнения? Смотрите код ниже и до встречи через миллиарды лет.
Код
import random
import matplotlib.pyplot as plt
import networkx as nx
import math as mt
from bitarray import bitarray
def distance(x1, y1, x2, y2):
return mt.sqrt((x2-x1)**2 + (y2-y1)**2)
INF = 2 ** 31-1
#random.seed(1)
n = 10
v1 = []
points = {}
for i in range(n):
points[i] = (random.randint(1,1000), random.randint(1,1000))
input_matrix = []
for i, vi in points.items():
m1 = []
for j, vj in points.items():
if i==j:
m1.append(INF)
else:
m1.append(int(distance(vi[0], vi[1], vj[0], vj[1])))
v1.append([i,j,int(distance(vi[0], vi[1], vj[0], vj[1]))])
input_matrix.append(m1.copy())
plt.figure(figsize=(8, 8))
graph = nx.Graph()
graph.add_nodes_from(points)
# Добавляем дуги в граф
for i in v1:
graph.add_edge(i[0], i[1], weight=i[2])
# -----------------------------------------------------------------
def calc_next(m, s, n, src):
min = INF
best = 255
for i, val in enumerate(s.tolist()):
if val == 0:
s0 = s.copy()
s0[i] = 1
if n>2:
sum = m[src][i]
r = calc_next(m, s0, n-1, i)
sum = sum + r[0]
temp = r[1]
else:
for j, val_j in enumerate(s0.tolist()):
if val_j == 0:
break
temp = [j]
sum = m[src][i] + m[i][j] + m[j][len(m)-1]
temp.append(i)
if sum < min:
min = sum
best = i
temp2 = temp.copy()
return [min, temp2]
#-----------------------------------------------------------------
s = bitarray(n-1)
s.setall(0)
r = calc_next(input_matrix, s, n-1, n-1);
r[1].append(n-1)
print('min:', r[0])
print(r[1])
d = []
s = r[1]
for i, v in enumerate(s):
d.append([int(s[i-1]), int(s[i])])
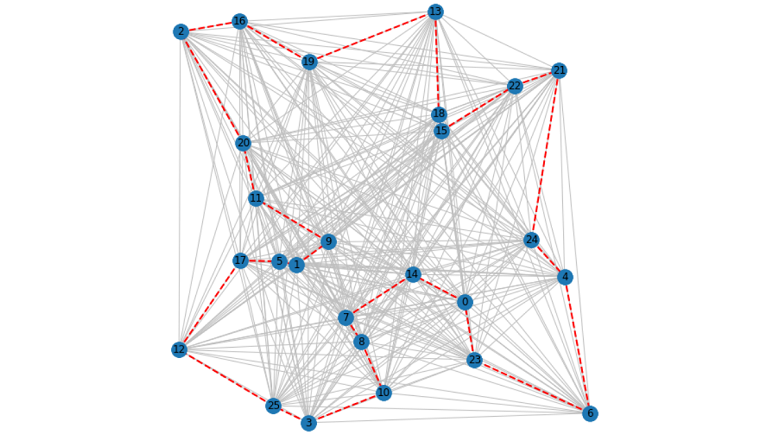
# Рисуем всё древо
nx.draw(graph, points, width=1, edge_color="#A0A0A0", with_labels=True)
nx.draw(graph, points, width=2, edge_color="blue", edgelist=d, style='dashed')Для остальных, кто не готов ждать столько времени, у нас есть другие методы решения.
2. Метод ветвления и границ с полным перебором
Отличный метод, хотя не прост для понимания, но на большинстве наборов данных даёт отличные результаты. Очень нестабильный по времени алгоритм, в некоторых ситуациях разница доходила более 1000 раз от среднего на типовых маршрутах. А самое печальное: нет возможности узнать, как долго ещё будет идти обработка, секунды или дни, всё случайно.
Что бы не ждать вечность и была использована попытка схитрить (не искать именно точное решение), отсекать маловероятные решения для уменьшения количества расчётов. Маловероятное событие не значит невозможное и один такой прокол послужил причиной недовольства руководителя, обыгранной выше.
Не оптимальный маршрут виден не вооружённым взглядом, если есть пересечение на графе.
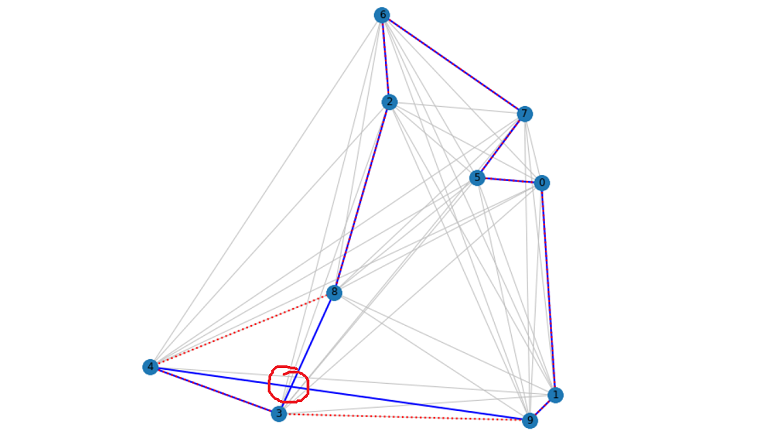
Отсутствие пересечения ещё не говорит об оптимальности маршрута, но вот их наличие говорит о явной не оптимальности.

Возможно, моя следующая статья будет именно об этом элегантном методе, в его честной реализации, но сегодня герой не он.
3. Метод динамического программирования
Суть метода в том, что выбирается город, а затем для всех остальных городов в связке с ним строятся все возможные маршруты и выбирается самый короткий. Алгоритм рекурсивно применяется для всех оставшихся городов за вычетом выбранного на предыдущем этапе и так до тех пор, пока не выбранными остаются только два города. Для симметричной задачи часть маршрутов будет повторяться, а если результат сохранять отдельно, то его нужно рассчитать всего один раз.
Алгоритм довольно известный, но возможно Вам будет любопытно увидеть авторскую реализацию. В ней мне хотелось максимально ускорить каждый шаг алгоритма. Были применены некоторые спорные ухищрения для его более эффективного машинного исполнения.
Тут и далее мы будем подразумевать следующее:
входные данные это матрица смежности расстояний между городами;
граф расстояний будет не ориентированным и симметричным;
маршрут будет замкнутым;
кольцевые маршруты запрещены (значение элементов главной диагонали входной матрицы будет проигнорировано);
для расчётов мы будем использовать множество натуральных чисел.
Задача коммивояжера может быть решена быстрее, чем за n!, если использовать дополнительную память, много дополнительной памяти.
В данной версии нужно совершить шагов алгоритма на любом наборе данных:
Но если учитывать только шаги, которые производят вычисления, а не считывают уже рассчитанные значения из памяти, то их окажется всего:
Это прекрасно, ведь мы можем точно сказать, сколько будут длиться вычисления. Однако самое замечательное свойство алгоритма в том, что скорость выполнения практически не изменяется от набора входных данных.
В процессе работы нам нужно хранить все возможные комбинации построенных маршрутов, а также длину минимального маршрута на данный момент.
Для этого нам понадобятся два массива дополнительной памяти по (n-1)*2(n-1) элементов. Первый нужен для хранения локальной суммы на шаге, а второй массив будет содержать путь к вершине, по которому нужно двигаться, чтобы выбрать кратчайший маршрут. Если в итоге нужна только величина оптимального решения, то от второго массива можно совсем отказаться, уменьшив время работы и объём используемой памяти.
Почему именно столько элементов, а не n*2n? На примере ниже мы видим массив для n = 4 элементов. По горизонтали отмечен путь в ту вершину, которую мы должны посетить, находясь в данном узле, а по вертикали числовое представление двоичной маски тех вершин, которые мы уже посетили к данному моменту.
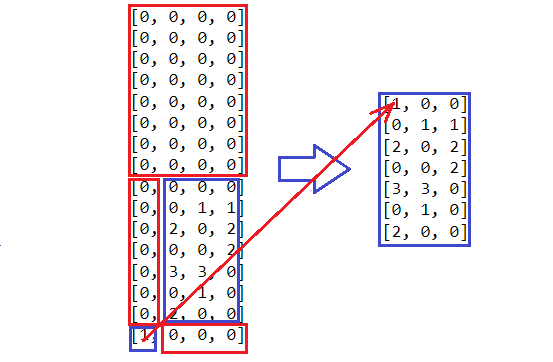
Можно заметить, что часть массива не используется. Это связанно с тем что, начиная обход всегда с нулевой вершины можно более чем вдвое уменьшить число необходимой памяти. Этого можно добиться переместив крайне левый нижний элемент в свободную область, а также сместив индексы на единицу. Такой манёвр достигается выделением из алгоритма отдельного первого шага, который немного отличается от остальных шагов. Конечно, ещё остаются свободные участки памяти, но бороться с ними уже вычислительно сложнее, мне видится это не рационально.
Мне думается, что использовать числа с плавающей точкой для точной задачи не совсем корректно. Да и работа с целыми числами при определённых условиях несколько быстрее. (Для Python это не так, но так как алгоритм портируемый, здесь оставлено как в оригинале). Все значения равные и выше MaxLongint (2,147,483,647) будем считать за бесконечность (inf). Это сделано для того, чтобы при сложении двух бесконечностей, у нас не происходило переполнение. Так мы экономим одну проверку на каждый шаг алгоритма.
Как результат, минимальный маршрут не должен быть больше или равен MaxLongint. Если данное условие не выполняется, считаем, что в графе нет разрешённого маршрута.
Вместо тысячи слов
import random
import matplotlib.pyplot as plt
import networkx as nx
import math as mt
from datetime import datetime
def distance(x1, y1, x2, y2):
return mt.sqrt((x2-x1)**2 + (y2-y1)**2)
INF = 2 ** 31-1
# random.seed(1)
n = 16
v1 = []
points = {}
for i in range(n):
points[i] = (random.randint(1,1000), random.randint(1,1000))
input_matrix = []
for i, vi in points.items():
m1 = []
for j, vj in points.items():
if i==j:
m1.append(INF)
else:
m1.append(int(distance(vi[0], vi[1], vj[0], vj[1])))
v1.append([i,j,int(distance(vi[0], vi[1], vj[0], vj[1]))])
input_matrix.append(m1.copy())
plt.figure(figsize=(8, 8))
graph = nx.Graph()
graph.add_nodes_from(points)
# Добавляем дуги в граф
for i in v1:
graph.add_edge(i[0], i[1], weight=i[2])
#-----------------------------------------------------------------
def tsp(input_matrix):
n = len(input_matrix)
# Генерация служебных массивов
s = (1 << (n - 1)) - 1
path = [0] * s
local_sum = [0] * s
for i in range(s):
path[i] = [0] * (n-1)
local_sum[i] = [-1] * (n-1)
m = [n - 1, input_matrix.copy(), path, local_sum]
sum_path = INF
for i in range(m[0]):
index = 1 << i
if s & index != 0:
sum_temp = tsp_next(m, s ^ index, i) + m[1][i + 1][0]
if sum_temp < sum_path:
sum_path = sum_temp
m[2][0][0] = i + 1
m[3][0][0] = sum_path
# Вывод оптимального пути
res = []
init_point = int(path[0][0])
res.append(init_point)
s = ((1 << m[0]) - 1) ^ (1 << init_point - 1)
for i in range(1, m[0]):
init_point = int(path[s][init_point - 1])
res.append(init_point)
s = s ^ (1 << init_point - 1)
res.append(0)
return [sum_path, res]
#-----------------------------------------------------------------
def tsp_next(m, s, init_point):
if m[3][s][init_point] != -1:
return m[3][s][init_point]
if s == 0:
return m[1][0][init_point + 1]
sum_path = INF
for i in range(m[0]):
index = 1 << i
if s & index != 0:
sum_temp = tsp_next(m, s ^ index, i) + m[1][i + 1][init_point + 1]
if sum_temp < sum_path:
sum_path = sum_temp
m[2][s][init_point] = i + 1
m[3][s][init_point] = sum_path
return sum_path
#-----------------------------------------------------------------
# Расчёт минимальной дистанции
start_time = datetime.now()
res = tsp(input_matrix)
print(datetime.now() - start_time)
print(res)
#-----------------------------------------------------------------
d = []
s = res[1]
for i, v in enumerate(s):
d.append([int(s[i-1]), int(s[i])])
# Рисуем всё древо
nx.draw(graph, points, width=1, edge_color="#C0C0C0", with_labels=True)
nx.draw(graph, points, width=2, edge_color="red", edgelist=d, style="dashed")Реализация на Python меня на столько разочаровала по скорости исполнения, что не нашёл ничего лучше, как подключить dll собранную на Pascal к скрипту. Скорость работы внешней функции оказалась раз в тридцать быстрее Пайтоновской, поэтому далее оценивал только её.
Мне не вполне удалось разобраться с передачей во внешнюю библиотеку списков Python, поэтому в данной реализации на вход передаётся строка. После завершения возвращается так же строка.
Выглядит это так
from ctypes import *
lib = cdll.LoadLibrary(r"../tsp_dynamic.dll")
lib.tsp_dynamic.restype = c_char_p
lib.tsp_dynamic.argtypes = [c_char_p]
result = lib.tsp_dynamic(str([n, input_matrix]).encode('utf-8')).decode('utf-8').split(',')library tsp_dynamic;
uses
SysUtils;
function tsp_dynamic(input: PChar): PChar; cdecl;
begin
// Обрабатываем ввод
…
// Возвращаем результат
tsp_dynamic := pChar('…');
end;
exports
tsp_dynamic;
end.Полный код + dll
import random
import matplotlib.pyplot as plt
import networkx as nx
import math as mt
from ctypes import *
from datetime import datetime
def distance(x1, y1, x2, y2):
return mt.sqrt((x2-x1)**2 + (y2-y1)**2)
# random.seed(1)
n = 21
v1 = []
points = {}
for i in range(n):
points[i] = (random.randint(1,1000), random.randint(1,1000))
input_matrix = []
for i, vi in points.items():
m1 = []
for j, vj in points.items():
if i==j:
m1.append(INF)
else:
m1.append(int(distance(vi[0], vi[1], vj[0], vj[1])))
v1.append([i,j,int(distance(vi[0], vi[1], vj[0], vj[1]))])
input_matrix.append(m1.copy())
plt.figure(figsize=(8, 8))
graph = nx.Graph()
graph.add_nodes_from(points)
# Добавляем дуги в граф
for i in v1:
graph.add_edge(i[0], i[1], weight=i[2])
#-----------------------------------------------------------------
start_time = datetime.now()
lib = cdll.LoadLibrary(r"../tsp_dynamic.dll")
lib.tsp_dynamic.restype = c_char_p
lib.tsp_dynamic.argtypes = [c_char_p]
res = lib.tsp_dynamic(str([n, input_matrix]).encode('utf-8')).decode('utf-8').split(',')
print(datetime.now() - start_time)
#-----------------------------------------------------------------
if res[0] != '':
for i in range(len(res)):
res[i] = int(res[i])
len1 = res.pop(0)
print([len1, res])
d = []
s = res
for i, v in enumerate(s):
d.append([int(s[i-1]), int(s[i])])
# Рисуем всё древо
nx.draw(graph, points, width=1, edge_color="#C0C0C0", with_labels=True)
nx.draw(graph, points, width=2, edge_color="red", edgelist=d, style="dashed")
Алгоритм динамического программирования имеет экспоненциальный рост от числа вершин графа, как по объёму вычислений, так и по объёму требуемой оперативной памяти. Уже на 28 вершинах на моём компьютере резко просела производительность, так как в системе закончилась свободная память и подключились механизмы свопинга.
Потенциально в текущей реализации можно обрабатывать графы до 32 размерности включительно, но я не думаю, что это хорошая идея. Тут как в казино, главное суметь вовремя остановиться. Каждое следующее увеличение размерности графа на единицу требует в два раза больше ресурсов, чем предыдущее.
В таком виде задача очень похоже на притчу о зёрнах и шахматной доске.
Решение далеко не Панацея, и всё же граф на 26 элементов за две минуты, это гораздо лучше, чем несколько миллиардов лет, согласитесь.

Комментарии (13)

gybson_63
25.11.2022 11:13На пайтоне так не программируют. Программируют как-то так
scipy.sparse.csgraph.shortest_path — SciPy v1.9.3 Manual
rebuilder Автор
25.11.2022 11:31+1Ну да, обычно дёргают готовую библиотеку, которая делает магию и всё. Я же хотел объяснить, как это происходит.

wataru
25.11.2022 12:54+1Удивительно, как вы смогли написать статью про решение задачи динамическим программированием и не сказать ни одного правильного слова про, собственно, динамическое программирование. Хоть бы статью на википедии процитировали, что ли.
И вообще вы алгоритм, как будто не поняли.
В процессе работы нам нужно хранить все возможные комбинации построенных маршрутов, а также длину минимального маршрута на данный момент.
Нет. Вообще нет. Алгоритм находит для каждого подмножества вершин кратчайший путь, начинающийся с 0 и заканчивающийся в заданной вершине. Тут 2 параметра — подмножество и последняя вершина. Это те самые подзадачи, упомянутые в википедии. И ответ на каждую такую подзадачу вы сохраняете. Поэтому вам и нужно столько памяти, чтобы все сохранить.
Оптимизация по памяти и времени достигается тем, что не надо рассматривать подзадачи, где последняя вершина 0 и также подмножества, где вершины 0 нет. Поэтому первый шаг и выделяется отдельно, ибо там считается основная задача, где вы начали с 0 и в 0 же вернулись.
Еще стоило написать, что тут рекурсивная реализация с мемоизацией.
Ну и имена переменных, конечно, ужасные. Что за m вообще? Плюс складывать разные по смыслу вещи в m[0], m[1] и m[2] и m[3] — очень усложняет чтение кода. На олимпиадах каких-нибудь это оправдано, но код в статье стоит немного причесать перед выкладыванием.

rebuilder Автор
25.11.2022 13:12Спасибо что вы не прошли мимо! Алгоритм как раз я понял хорошо, возможно выразил не совсем академично, но благодаря Вам, всё стало гораздо яснее. А мне ещё расти над собой.
Жаль, что вы не высказались за сам подход.

wataru
25.11.2022 13:19+1В смысле — за сам подход? Алгоритм — хороший, сильно быстрее полного перебора или метода ветвей и границ. Имеет свои ограничения и сильно больше 30 вершин не потянет, ну так задача NP-полная, все алгоритмы экспоненциальные и медленные.
Огромный вам плюс в статью, что при всех небольших недочетах описания, реализация правильная.

dpetrucii
25.11.2022 18:44+2Мне всегда казалось, что метод ветвей (кстати, не ветвлений) и границ самый простой для понимания способ решения этой задачи. И при его наличии полный перебор можно даже не упоминать, ведь он по сути и есть способ перебора.


dyanishev
А не проще было всё это реализовать через NumPy, чем возиться с подключением собственной библиотеки и передачей данных через строки?
rebuilder Автор
Проще конечно же! Но вот быстрее ли, сомнительно. Возможно Вы сможете доказать обратное.
Да и код для библиотеки уже существовал, нужно было только обернуть функцию.
dyanishev
Ну вот Вам снизу написали про готовую функцию на SciPy - можно ее ради интереса сравнить по быстродействию с Вашей dll-кой, чтобы самому не морочиться с повторной реализацией алгоритма на NumPy. SciPy как раз с использованием массивов NumPy сделан. А NumPy в свою очередь использует библиотеки, написанные на Fortran и C. Так что с весьма большой долей вероятности реализация на NumPy будет или сравнима с Вашей или даже быстрее.
P.S. - ни к чему Вас не призываю, просто заметил, что серьезную математику на чистом Питоне программировать - дело не очень продуктивное.
gybson_63
У вас списки, в которых лежат не числа, а объекты похожие на числа. Медленнее такого уже не сочинить. Но этот код довольно просто переписать на numpy и поразиться тому, что пайтон реально быстрый.