Привет, Хабр! В данной статье будет рассмотрено применение логистической регрессии, причинного случайного леса (Causal Random Forest), метода CUPED для оценки изменения целевой переменной в Python при проведении А/Б тестов. Основное внимание будет уделено практике, теоретические аспекты методов будут упомянуты вскользь.

Условие: есть датасет компании, которая продает на своем сайте билеты на транспорт и которая зарабатывает на наценке. Аналитик проводит АБ-тест: А и Б - разные варианты новой ценовой политики - наценка 4% или 9%.

Вопрос: какую из двух вариантов наценки нужно устанавливать и почему.

Датасет можно скачать здесь. Подробное описание данных лежит здесь. 

Для понимания достаточно знать, что есть две целевые переменные “buy” (факт совершения покупки), “total profit” (прибыль) и основные ковариаты:

1. T - тритмент переменная (0 или 1), показывающая вариант ценообразования А или В;

2. bus_offers_count - количество предложений в выдаче;

3. price_mean, price_min, price_max, price_std - характеристики цены в выдаче;

4. final_rating_mean, final_rating_min, final_rating_max, final_rating_std - характеристики рейтинга в выдаче;

5. dist - расстояние, на котором осуществляется перевозка (км) 

Рассмотрим влияние введения наценки на факт совершения покупки (“buy”) и на прибыль (“total_profit”).

Загружаем данные.

```

import pandas as pd

df = pd.read_excel('data.xlsx')

df.head(5)

```

Для оценки влияния на факт совершения покупки (“buy”) построим логистическую регрессию. Перед построением логистической регрессии проверим, соблюдается ли баланс ковариат, а также есть ли мультиколлинеарность. 

Если баланс ковариат соблюдается, то мы можем сделать вывод, что группы похожи по ковариатам и эксперимент проведен “честно”. 

```    

def balance_covariate(df):

        number_of_treated=len(df.query('T==1'))

        number_of_control=len(df.query('T==0'))

        covariate_table_mean=pd.DataFrame(df.groupby(["T"],     as_index=True).mean()).drop(columns=["buy", "total_profit"]).T.rename(columns={0:   'mean_control', 1: 'mean_treat'}).T

        covariate_table_var=pd.DataFrame(df.groupby(["T"], as_index=True).var()).drop(columns=["buy", "total_profit"]).T.rename(columns={0: 'var_control', 1: 'var_treat'}).T

        frames=[covariate_table_mean, covariate_table_var]

        result = pd.concat(frames).T

        t_stat=[]

        for i in range(0, len(result)):

            numerator=result['mean_control'][i]-result['mean_treat'][i]

            denominator=((result['var_control'][i]/number_of_control) + (result['var_treat'][i]/number_of_treated))(1/2)

            t_stat.append(numerator/denominator)

        result['t_статистика']=t_stat

        p_value=[]

        for i in range(0, len(result)):

            if abs(result['t_статистика'][i]) <= 1.645 :

                p_value.append('')

            elif abs(result['t_статистика'][i]) <= 1.96:

                p_value.append('')

            elif abs(result['t_статистика'][i]) <= 2.58:

                p_value.append('')

            else:

                p_value.append(' ')

        result['значимость']=p_value

        return(result.round(3))

    balance_covariate(df)

```

Для всех ковариат не отвергаем гипотезу о равенстве средних на 1%-ном уровне значимости, кроме нескольких переменных, которые значимы на 5% и 10%-ном уровне значимости. Полностью таблицу можно посмотреть в ноутбуке.

Строим корреляционную матрицу. Для удобства анализа выведем все коэффициенты корреляции, которые по модулю больше 0,5.

```    

import matplotlib.pyplot as plt

    import seaborn as sns

    dfCorr = df.drop(['ID'], axis=1).corr()

    filteredDf = dfCorr[((dfCorr >= .5) | (dfCorr <= -.5)) & (dfCorr !=1.000)]

    for column in filteredDf.columns:

        if filteredDf[column].isna().sum() == len(filteredDf):

            filteredDf=filteredDf.drop(column, axis=1)

            filteredDf=filteredDf.drop(column)

    sns.heatmap(filteredDf, annot=True, vmin=-1, vmax=1, center= 0, cmap= 'coolwarm')

    plt.show()

```

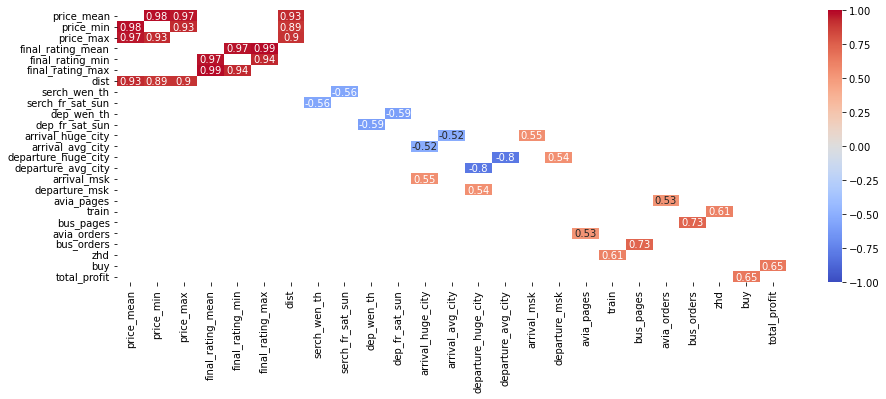
В данных присутствуют ковариаты, коэффициент корреляции между которыми больше 0,9, что подтверждает наличие высокой мультиколлениарности между переменными (Картаев, 2019). 

Рассчитаем VIF. Для удобства интерпретации результатов выведем VIF, которые больше 10, который говорит о наличии мультиколлениарности между переменными (Картаев, 2019).

```    

from statsmodels.stats.outliers_influence import variance_inflation_factor

    def vif(data):

        vif_data = pd.DataFrame()

        vif_data["feature"] = data.columns

        vif_data["VIF"] = [variance_inflation_factor(data.values, i)

                              for i in range(len(data.columns))]

        return(vif_data)

    vif_df=vif(df)

    vif_df[vif_df["VIF"]>=10]

```

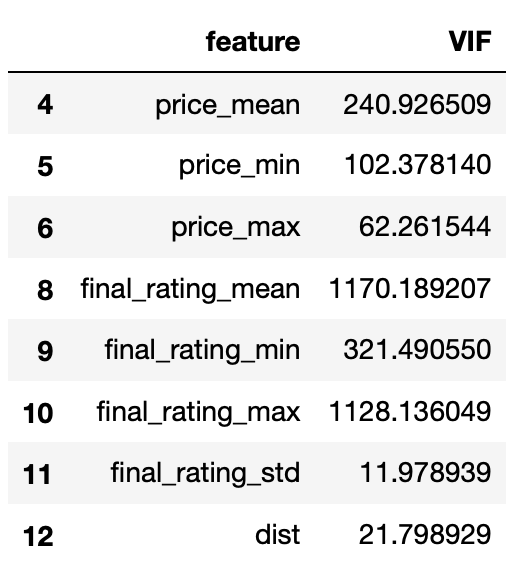
Результаты расчета матрицы корреляции и VIF совпадают: существует высокая мультиколлинеарность между переменными price_mean, price_min, price_max; final_rating_mean, final_rating_min, final_rating_max, final_rating_std; dist. Неудивительно, так как эти переменные - разные характеристики одной и той же величины. Чтобы избежать мультиколлинеарности, из переменных, перечисленных выше, оставим только price_mean, final_rating_mean, final_rating_std, dist. 

```    

df=df.drop(columns=['price_min', 'price_max', 'final_rating_min', 'final_rating_max'])

    vif_df=vif(df)

    vif_df[vif_df["VIF"]>=10]

```

После этого в наших данных все равно сохраняется мультиколлинеарность. Но какую-то из этих переменных я не буду выбрасывать, так как существует вероятность выкинуть значимую переменную, что приведет к смещению оценок и получению некорректных результатов. 

Перейдем от предобработки данных к построению логистической регрессии. Но проблема большого количества ковариат осталась (у нас их 34). Поэтому мы будем строить не простую логистическую регрессию, а логистическую регрессию с регуляризацией L1, L2 и elastic net и сравним результаты. 

Сутейно: регуляризация - метод, который добавляет дополнительный штраф за сложность модели к минимизируемой функции потерь, то есть менее важным характеристикам регуляризация придает меньший вес. Регуляризация L1 (Lasso) может как обнулить значения некоторых коэффициентов, так и придать им меньший вес.

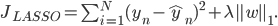
В то время как регуляризация L2 (Ridge/регуляризация Тихонова) не может обнулить значения коэффициентов, но может придать им меньший вес. 

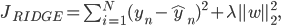
Elastic net - объединение подходов L1 и L2 - те коэффициенты, которые были занулены при регуляризации L1, в elastic net будут иметь меньшие веса, чем при регуляризации L2. 

Для удобства интерпретации выведем таблицу со значением значимых коэффициентов. 

```    

import numpy as np

    from sklearn.metrics import accuracy_score

    from sklearn.model_selection import train_test_split

    from sklearn.linear_model import LogisticRegression

    from scipy.stats import norm

    def building_logistic_regression(df):

    

        def logreg_coef(logreg):

            coef=[]

            coef_list=logreg.coef_.tolist()[0]

            coef.append(logreg.intercept_)

            for i in range(0, len(coef_list)):

                coef.append(coef_list[i])

            return(coef)

    

        def logit_p1value(model, x):

            p1 = model.predict_proba(x)

            n1 = len(p1)

            m1 = len(model.coef_[0]) + 1

            coefs = np.concatenate([model.intercept_, model.coef_[0]])

            x_full = np.matrix(np.insert(np.array(x), 0, 1, axis = 1))

            answ = np.zeros((m1, m1))

            for i in range(n1):

                answ = answ + np.dot(np.transpose(x_full[i, :].astype(float)), x_full[i, :].astype(float)) * float(p1[i,1]) * float(p1[i, 0])

            vcov = np.linalg.inv(np.matrix(answ))

            se = np.sqrt(np.diag(vcov))

            t1 =  coefs/se  

            p1 = (1 - norm.cdf(abs(t1))) * 2

            return p1

    

        def confidence(x):

            return ('' if x <= 0.01 else ('**' if x <= 0.05 else ('*' if x<= 0.1 else ' ')))

    

        covariates=(df.columns.drop(['total_profit', 'buy']).to_list())

        X=df[covariates]

        y=np.ravel(df['buy'])

        result_logistic_dict={'covariates': ['intercept'] + covariates}

        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=21)

        methods=['l1', 'l2', 'elasticnet']

    

        conf=np.vectorize(confidence)

    

        for method in methods:

            if method== 'elasticnet':

                logreg = LogisticRegression(penalty=method, solver='saga', n_jobs=-1, multi_class='ovr', max_iter=10000, l1_ratio=0.5)

            else:

                logreg = LogisticRegression(penalty=method, solver='saga', n_jobs=-1, multi_class='ovr', max_iter=10000)

            logreg.fit(X_train, y_train)

            result_logistic_dict[method]=logreg_coef(logreg)

            result_logistic_dict[method + str('_confidence')]=conf(logit_p1value(logreg_l1, X))

        res=pd.DataFrame(result_logistic_dict)

        return(res)

    results = building_logistic_regression(df)

    results[results["l1_confidence"] != ' ']

```

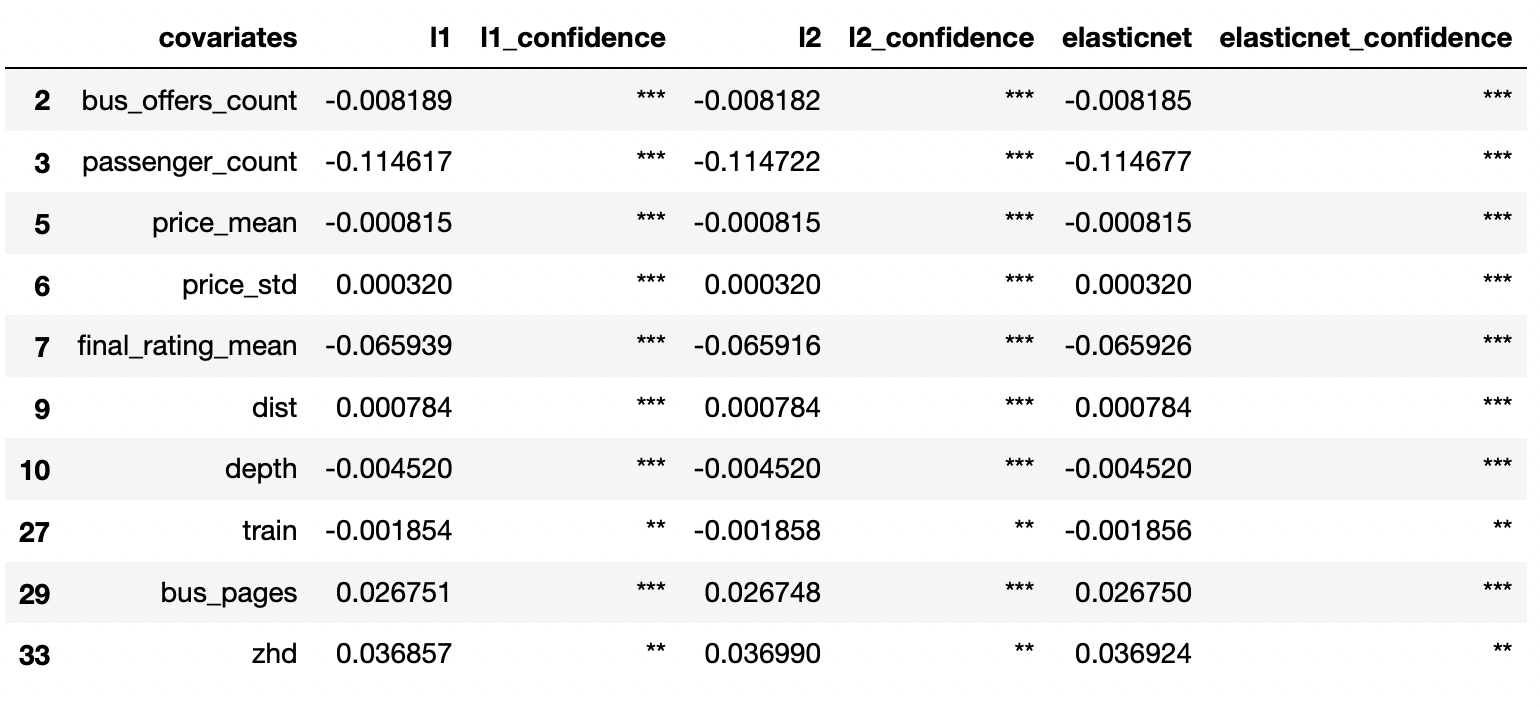
Коэффициент при переменной treatment незначимый, следовательно, согласно логистической регрессии мы не можем утверждать, что введение 9%-ной наценки влияет на факт совершения покупки билета. 

Логистическая регрессия не учитывает следующий нюанс: при проведении эксперимента на целевой признак может влиять не только наличие какого-либо treatment, но и ковариаты – характеристики наблюдения (см. Рисунок 2). 

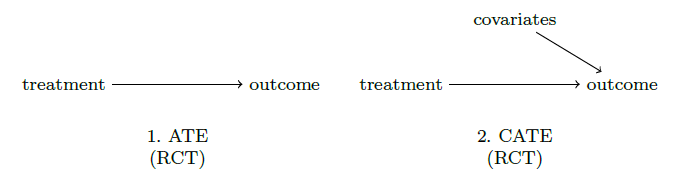
Из этого следует, что внутри каждой группы эффект воздействия будет разный. Одним из методов определения наиболее важных ковариат в части «вложения» в эффект воздействия является причинный случайный лес (causal random forest). Причинный случайный лес похож на случайный лес. В то время как случайный лес делает сплит, основываясь на следующих критериях: ошибке классификации, энтропии или индексу Джини, причинный случайный лес делает сплит таким образом, чтобы максимизировать разницу эффекта воздействия между ветками дерева(Athey and Imbens (2016)).

Построим причинный случайный лес для нашего примера и выведем коэффициент при Т. Важно учесть, что алгоритм причинного случайного леса позволяет выделить наиболее важные характеристики, то есть характеристики, которые больше всего влияют на целевую метрику при попадании в тритмент, поэтому мы можем добавить все характеристики в модель, не переживая о мультиколлинеарности - алгоритм решит все за нас.

```    

from econml.dml import CausalForestDML

    from sklearn.linear_model import LogisticRegressionCV

    import numpy as np

    def CATE(df, y, X, model_t, model_y):

        X=df[X]

        Y=np.ravel(df[y])

        T = df['T']

        W=None

        causal_forest_buy = CausalForestDML(model_t= model_t,

                        model_y= model_y,

                        criterion='het', n_estimators=100,       

                        min_samples_leaf=30, 

                        max_depth=5, max_samples=0.5,

                        discrete_treatment=True, cv=12, min_samples_split=50, random_state=23)                      

        causal_forest_buy.fit(Y, T, X=X, W=W) 

        return(causal_forest_buy)

    CATE_buy=CATE(df, 'buy' ,df.columns.drop(['total_profit', 'buy', 'T']).to_list(),

                 model_t= LogisticRegressionCV(solver='sag', max_iter=1000, tol=0.01, multi_class='ovr', random_state=23),

                 model_y= LogisticRegressionCV(solver='sag', max_iter=1000, tol=0.01, multi_class='ovr', random_state=23))

    CATE_buy.const_marginal_ate_inference(df[df.columns.drop(['total_profit', 'buy', 'T']).to_list()])

```

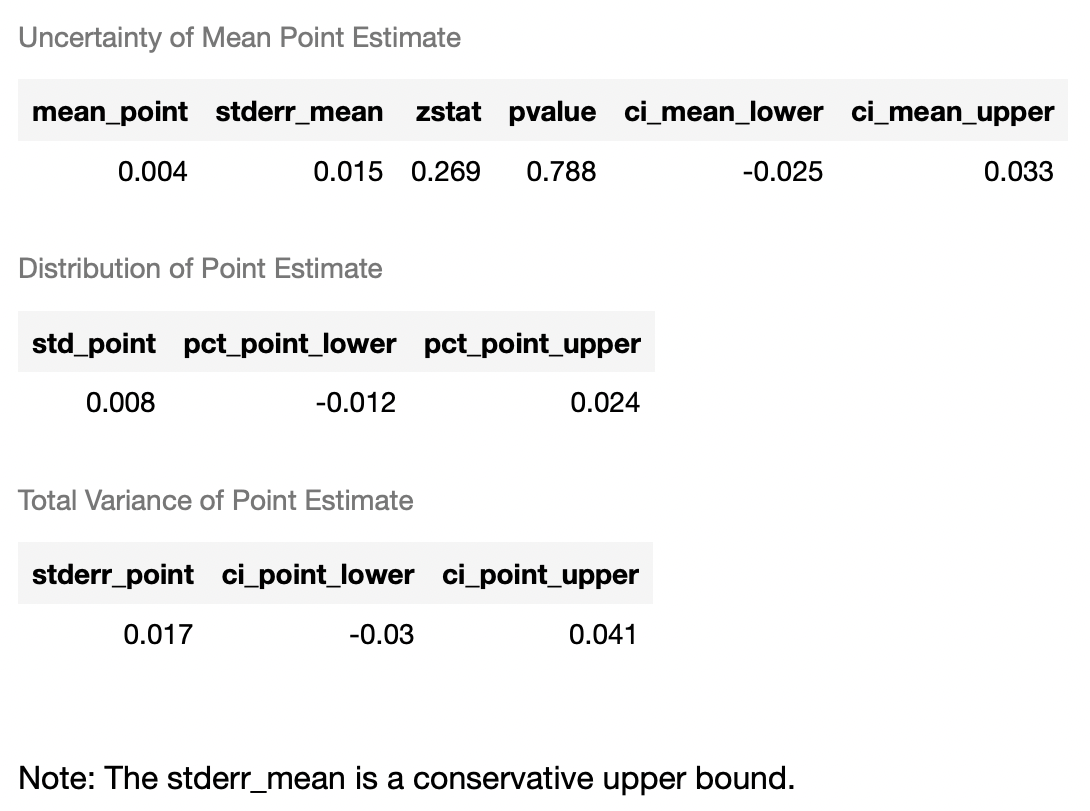
Мы не можем интерпретировать результаты, так как p-value очень большой и эффект статистически не значим даже на 15%-ном уровне значимости. Но построение причинного случайного леса и библиотека SHAP в Python позволяет визуализировать, какие характеристики при разделении деревьев оказались наиболее важными и как изменение характеристики влияет на результат при попадании в тритмент группу. В библиотеке SHAP для оценки важности характеристик рассчитывают значения Шепли. Понятийно происходит оценка предсказаний модели с и без данной характеристики. Формально (см. Рисунок 3):

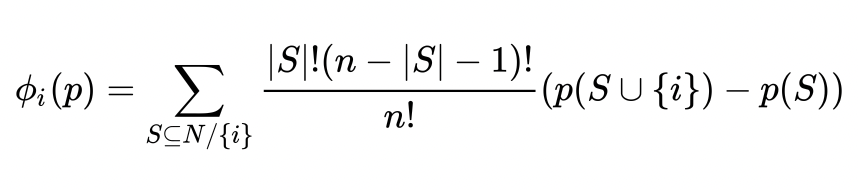
P (S U {i})— это предсказание модели с i-той характеристикой,

p(S) — это предсказание модели без i-той характеристики,

n — количество характеристик,

S — произвольный набор фичей без i-той характеристики.

Визуализируем важность характеристик с помощью библиотеки SHAP.

```    

shap_values = causal_forest_buy.shap_values(X)

shap.summary_plot(shap_values['Y0']['T'])

```

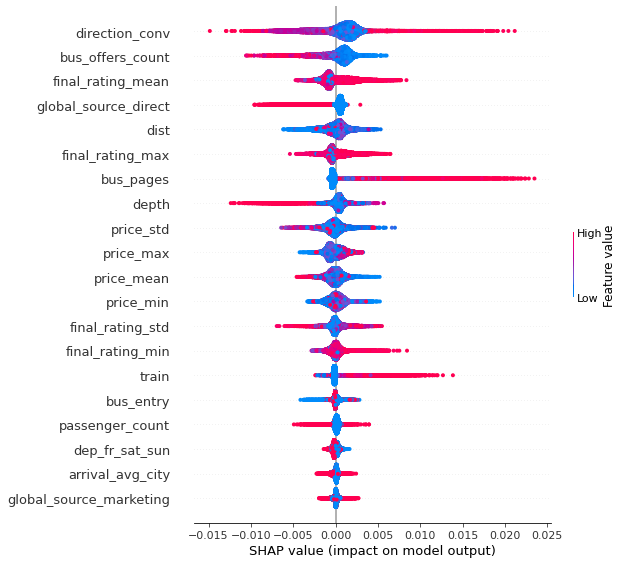
В зависимости от характеристик, влияние введения бОльшей наценки на факт совершения покупки может быть как положительным, так и отрицательным. Из рисунка 4 мы можем сделать следующие выводы (более структурировано - в таблице 4). В тритмент группе (в группе с наибольшей наценкой):

1. чем больше глубина поиска, тем вероятность покупки билета меньше (у человека есть время поискать билеты без наценки);

2. количество предложений в выдаче снижает вероятность покупки билета (скорее всего люди, видя большое количество предложений в выдаче, не боятся остаться без билета в нужный момент, поэтому, видя дороговизну билетов, уходят с сайта);

3. если пользователь пришел в сервис через поисковик (а не, например,  с приложения), то вероятность, что он купит билет, меньше (постоянные клиенты имеют привычку покупать в одном и том же сервисе, несмотря на подорожание);

4. чем выше количество посещений страницы с билетами на автобус/поезд, тем выше вероятность покупки билета с наценкой (вероятно, человек боится еще бОльшего подорожания в будущем и решает не откладывать покупку).

Таблица 4: Влияние более высокой наценки на вероятность покупки в зависимости от показателя характеристики в разрезе групп от наиболее важной к наименее важной

А теперь посмотрим как введение наценки влияет на “total_profit” (прибыль компании). Из нашего датасета оставим только тех людей, которые совершили покупку, то есть “total_profit” которых > 0.

```

df_not_null_profit=df[df['total_profit'] > 0]

```

Баланс ковариат соблюдается. Полную таблицу с выводом можно посмотреть здесь.

```

balance_covariate(df_not_null_profit)

```

Посмотрим усредненную оценку влияния введения оценки на прибыль с помощью метода CUPED. В рамках метода CUPED необходимо брать только те переменные, которые не изменились во времени (X const), то есть были одинаковыми для наблюдения до эксперимента и после него (Xie, Aurisset, 2016). Это позволяет снизить дисперсию оценки. Эффект рассчитывается следующим способом:

1. Строим регрессию Y ~ X const => e(Y)

2. Для каждого наблюдения рассчитываем: Y_tilde = e(Y) + Y

3. Y ~ T => находим коэффициент при Т

```

import statsmodels.formula.api as smf

import numpy as np

X_pred='avia_pages + train + etrain + bus_pages + tours + avia_orders + bus_orders + zhd'

df_not_null_profit['total_profit_tilde']=smf.ols('total_profit ~' + str(X_pred), data=df_not_null_profit).fit(cov_type="HC3").resid + np.mean(df['total_profit'])

smf.ols('total_profit_tilde ~ T',     data=df_not_null_profit).fit(cov_type="HC3").summary().tables[1]

```

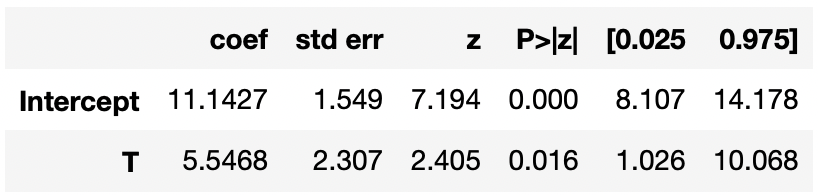
Введение бОльшей наценки увеличивает прибыль на 5,7 условных единиц с покупки на 5%-ном уровне значимости при прочих равных условиях. Минус метода CUPED - невозможность посмотреть гетерогенный эффект в разрезе разных характеристик. Построим причинный случайный лес и продемонстрируем гетерогенный эффект в разрезе разных характеристик.

```

CATE_total_profit=CATE(df_not_null_profit, 

                       'total_profit', 

                       df_not_null_profit.columns.drop(['total_profit', 'buy', 'T', 'total_profit_tilde']).to_list(),

                       model_t=LogisticRegressionCV(solver='saga', max_iter=2000, tol=0.001, multi_class='ovr', random_state=22), 

                       model_y='auto')

    CATE_total_profit.const_marginal_ate_inference(df_not_null_profit[df_not_null_profit.columns.drop(['total_profit', 'buy', 'T', 'total_profit_tilde']).to_list()])

```

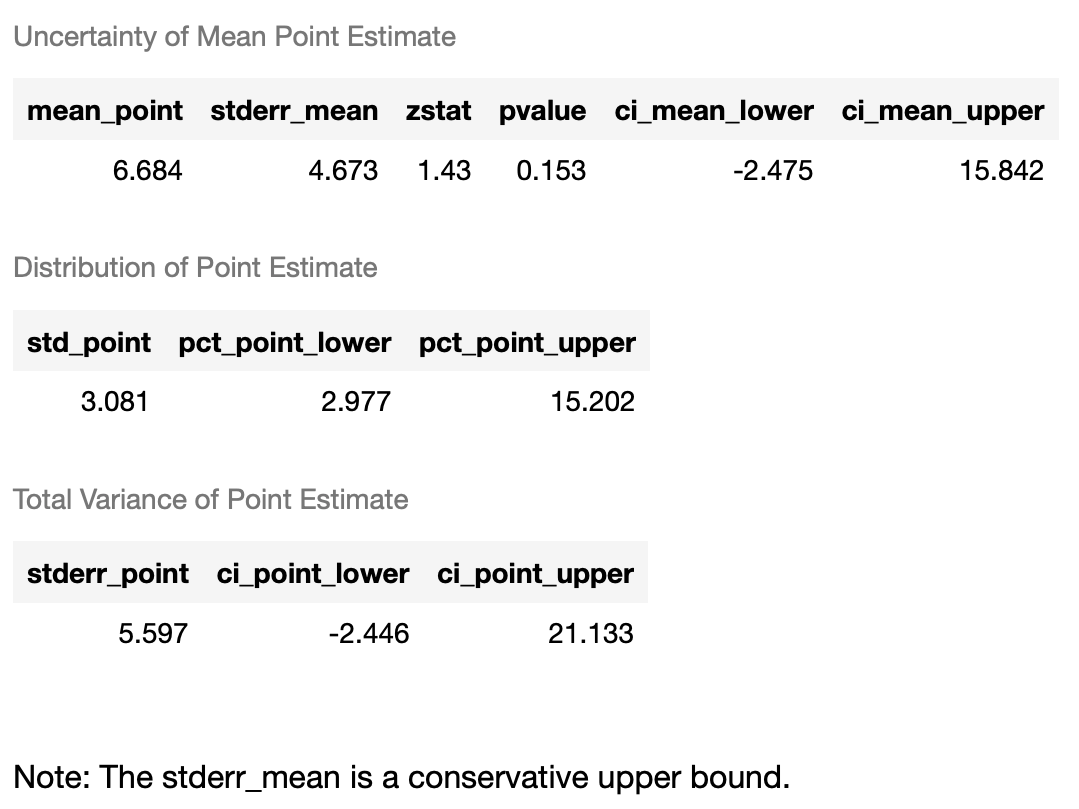
Причинный случайный лес показал следующий результат: введение бОльшей наценки увеличивает прибыль на 6,7 условных единиц с покупки на 15%-ном уровне значимости при прочих равных условиях.

```

shap_values = CATE_total_profit.shap_values(df_not_null_profit[df_not_null_profit.columns.drop(['total_profit', 'buy', 'T', 'total_profit_tilde']).to_list()])

shap.plots.beeswarm(shap_values['Y0']['T_1'])

```

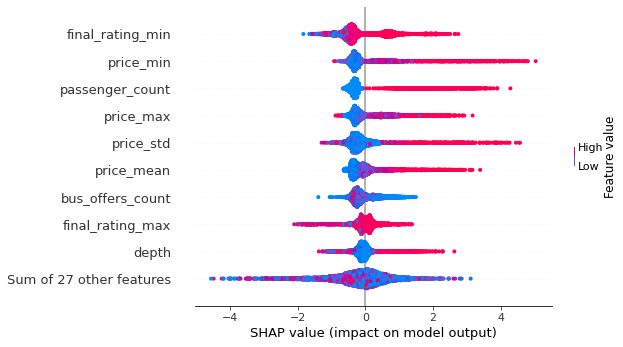
Из рисунка 5 мы можем сделать следующие очевидные выводы: при более высоком рейтинге, цене, количеству пассажиров прибыль во время продажи билетов с 9%-ной наценкой (а не 5%-ной) увеличивается.

Возвращаясь к стратегии компании, то решение о проценте наценки необходимо принимать в зависимости от целей. Если цель компании - получить наибольшую прибыль, то необходимо вводить наценку: всегда будут находиться богатые люди, для которых время слишком ценное, чтобы искать другие варианты или которые настолько богатые, что не будут замечать наценку на поездку.

Но если целевая метрика компании - увеличение количества клиентов, то наценку нужно оставлять низкой.

Компании также может попробовать миксовать стратегии: с одной стороны, оставить меньшую оценку, с другой, ввести бОльшую наценку на самые дорогие направления (например, на верхний 10%-ный перцентиль) и на поездки на сегодняшний/завтрашний дни.

Список литературы:

[1] Филипп Картаев “Введение в эконометрику”: учебник. – М.: Экономический фа- культет МГУ имени М.В. Ломоносова, 2019. – 472 с. ISBN 978-5-906932-22-8

[2] Jacob, Daniel, CATE meets ML - Conditional Average Treatment Effect and Machine Learning (March 30, 2021). Available at SSRN: https://ssrn.com/abstract=3816558 or http://dx.doi.org/10.2139/ssrn.3816558

[3] Scott M. Lundberg, Gabriel G. Erion, and Su-In Lee - Consistent Individualized Feature Attribution for Tree Ensembles (March 7, 2019) Available: https://arxiv.org/pdf/1802.03888.pdf 

[4] Xie, Huizhi and Juliette Aurisset. “Improving the Sensitivity of Online Controlled Experiments: Case Studies at Netflix.” Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (2016): n. pag.