Построение моделей на панельных данных в Python, часть 1: объединенный МНК, модель с фиксированными эффектами, модель со случайными эффектами.

Привет, Хабр!

В данной серии статей рассматривается построение “обычных” моделей на панельных данных в Python: объединенной модели МНК (pooled OLS), однонаправленной модели с фиксированными эффектами (one-way individual FE), двунаправленной модели с фиксированными эффектами (two-way FE), однонаправленной модели со случайными эффектами (one-way RE). Также будет рассмотрена оценка эффекта методом “разность разностей” (diff-in-diff) и методом "синтетический контроль". Основное внимание будет уделено практике, теоретические аспекты методов будут упомянуты для базового понимания.

Контекст: Данная статья сделана отдаленно по мотивам статьи “Online platform price parity clauses: Evidence from the EU Booking.com case” (Mantovani, Piga, Reggiani, 2021) [1]. Текст статьи, описание переменных, данные можно скачать здесь.

В Италии и Франции сайт Booking.com мог устанавливать потолок цен на стоимость жилья, которое выставлялось на сайте. 6 августа 2015 года во Франции был принят закон Макрона, который исключил из договоров между отелями и Booking.com пункты, запрещавшие отелям продавать номера по ценам ниже, чем у Booking.com. Целью закона Макрона - не допустить монопольного положения Booking.com. Французские отельеры поздравляли себя с принятием этого закона, так как считали, что, если отель предложит такие же цены, как на Booking.com, или даже ниже, то клиент предпочтет забронировать комнату на сайте отеля. В Италии такой закон принят не был.

Задача: Необходимо оценить, как изменились цены на номера в отелях после введения закона.

Итак, импортируем данные.

import pandas as pd
df = pd.DataFrame(pd.read_stata('data_mac_sr.dta'))
df.head(5)

Предобрабатываем данные - вычленяем регион.

df['region']=df.region.apply(lambda x: x.split(' ')[0])

Наши данные содержат информацию об отелях двух островов - Сардинии (Италия, закон не был принят), Корсики (Франция, закон о запрете вмешательства Booking.com был принят). По географическому признаку регионы похожи (см. Рисунок 1). 

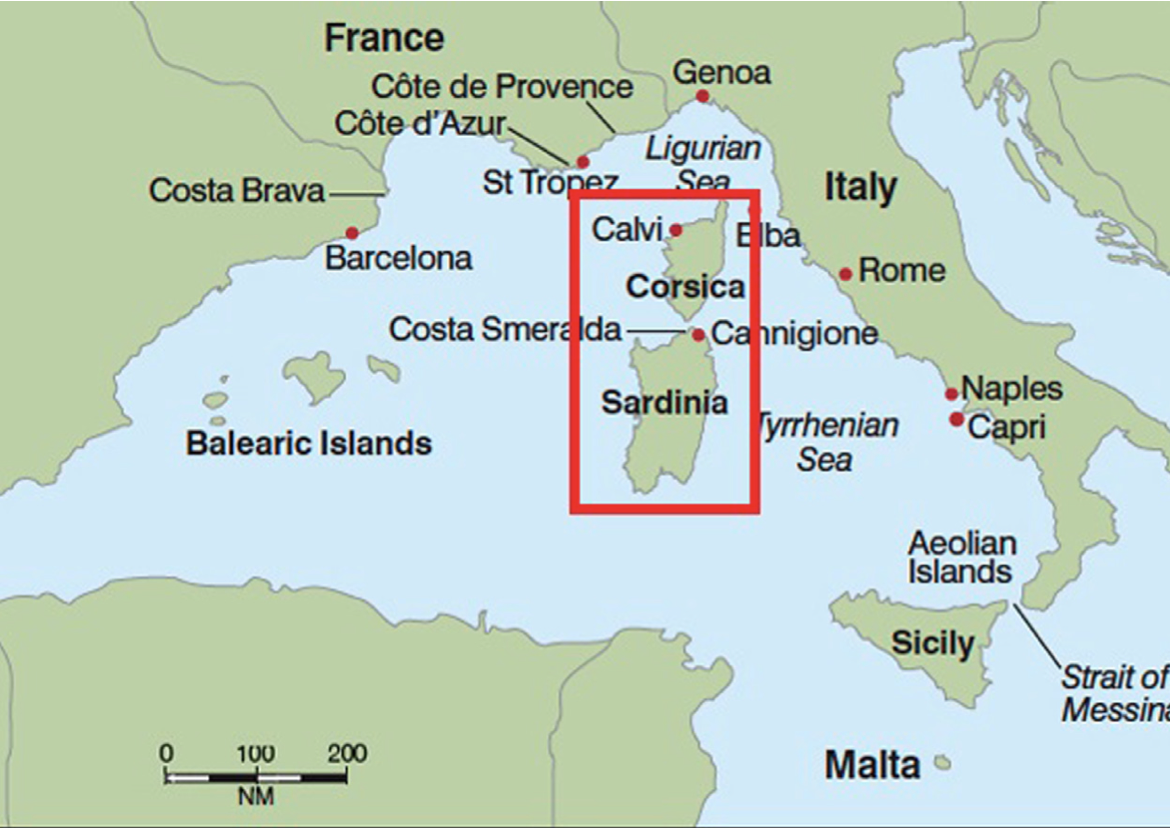
Датасет содержит данные за 4 месяца 2015 года: с июня по октябрь 2015 года. Данные панельные: одно наблюдение может попадать в датасет несколько раз. Чтобы проверить “похожесть” островов и по характеристикам отелей, построим баланс ковариат на самую раннюю дату попадания в датасет для каждого отеля, так как нам важно посмотреть на однородность отелей до анонса закона Макрона. После воздействия структура отелей на островах могла поменяться. Но нам это неважно.

Выбираем “самые ранние” показатели отелей.

df_table=df.merge(df.groupby('urlnum', as_index=False).agg({'date_src':'min'}))

Выбрасываем пропущенные значения.

df_table=df_table[['region', 'capacity',  'stars', 'rating',   
                    'dchain', 'Nreviewers',  'date_start_booking']].dropna()

Создаем колонку - количество дней от 00-00-0000, которая впоследствии пригодится при расчете стандартного отклонения.

df_table['for_std_counting']=df_table['date_start_booking'].dt.day 
                              + df_table['date_start_booking'].dt.month * 30 
                              + df_table['date_start_booking'].dt.year * 365

Строим баланс ковариат.

import numpy as np

def balance_covariate (df):

    t2=pd.concat([df[df['region']=='Corsica'].describe(
                datetime_is_numeric=True).round(2)[['capacity', 
                'stars', 'rating', 'dchain', 'Nreviewers', 
                'date_start_booking']].loc[['count', 'mean', 
                'std']].T.rename(columns={'mean': 'mean_Corsica', 
                'std': 'std_Corsica', 'count': 'obs_Corsica'}).T,

                df[df['region']=='Sardinia'].describe(
                datetime_is_numeric=True).round(2)[['capacity', 
                'stars', 'rating', 'dchain', 'Nreviewers', 
                'date_start_booking']].loc[['count', 'mean', 
                'std']].T.rename(columns={'mean': 'mean_Sardinia', 
                'std': 'std_Sardinia', 'count': 'obs_Sardinina'}).T])

    t2['date_start_booking']=t2['date_start_booking'].apply(
                lambda x: x.strftime('%Y-%m-%d') 
                if type(x) == pd._libs.tslibs.timestamps.Timestamp else x)

    t2=t2.rename(columns={'capacity': 'Number of rooms', 'stars' : 'Star rating',
                'dchain':'Chain affiliation', 'rating' : 'Users' rating',
                'Nreviewers' : 'Number of reviewers', 'date_start_booking' : 'On Booking.com since'}).T
    t2['std_Corsica'][-1]=round(np.std(df_table[df_table['region']=='Corsica'].for_std_counting),2)
    t2['std_Sardinia'][-1]=round(np.std(df_table[df_table['region']=='Sardinia'].for_std_counting),2)

    t_stat=[]
    for i in range(0, len(t2)):
        try:
                  numerator=int(t2['mean_Sardinia'][i])-int(t2['mean_Corsica'][i])
        except ValueError:
                  date1=(int(t2['mean_Sardinia'][i].split('-')[0]) * 365 + 
                  int(t2['mean_Sardinia'][i].split('-')[1].split('-')[0]) * 30 
                  + int(t2['mean_Sardinia'][i].split('-')[1].split('-')[-1])) 
                  date2= (int(t2['mean_Corsica'][i].split('-')[0]) * 365 + 
                  int(t2['mean_Corsica'][i].split('-')[1].split('-')[0]) * 30 
                  + int(t2['mean_Corsica'][i].split('-')[1].split('-')[-1]))
                  numerator = part1-part2
        denominator=((t2['std_Corsica'][i]2/t2['obs_Corsica'][i]) + (t2['std_Sardinia'][i]2/t2['obs_Sardinina'][i]))(1/2)
        t_stat.append(numerator/denominator)

    t2['t_статистика']=t_stat
    p_value=[]
    for i in range(0, len(t2)):
        if abs(t2['t_статистика'][i]) <= 1.645 :
            p_value.append('')
        elif abs(t2['t_статистика'][i]) <= 1.96:
            p_value.append('')
        elif abs(t2['t_статистика'][i]) <= 2.58:
            p_value.append('')
        else:
            p_value.append(' ')
    t2['значимость']=p_value
    t2=t2.round(2)
    return (t2)

balance_covariate(df_table)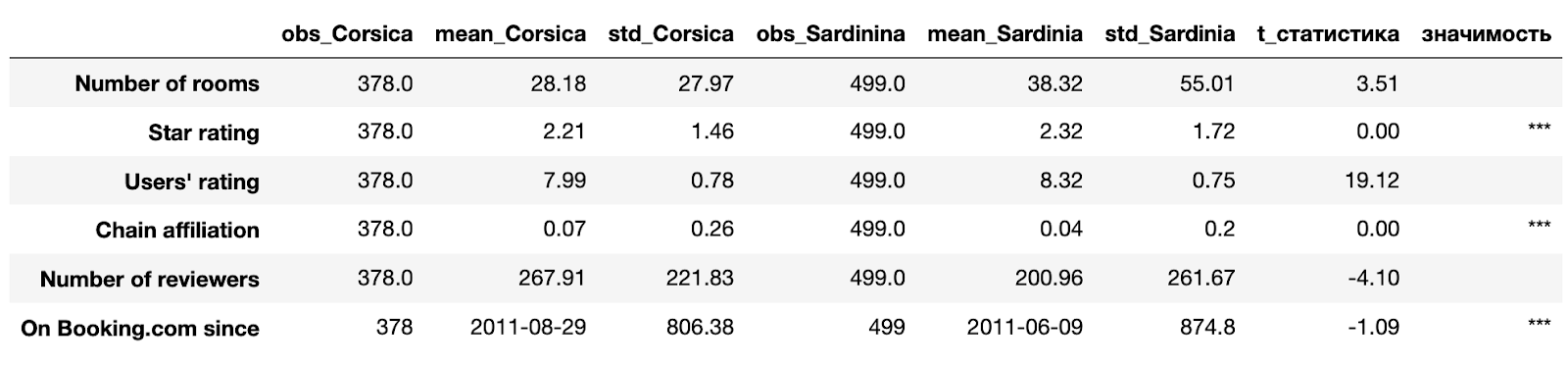

Тест Стьюдента показал, что на 1%-ном уровне значимости у отелей на островах Корсики и Сардинии одинаковы следующие характеристики: рейтинг, доля сетевых отелей, момент регистрации на Booking.com. Что же касается других характеристик, то тест Стьюдента отверг гипотезу о равенстве средних даже на 10%-ном уровне значимости. В реальной жизни данные неидеальные, тем не менее в нашем случае они не отличаются разительно - порядок цифр остается тем же.

Переименовываю столбцы для удобства использования таблицы и выбрасываю наблюдения с пропущенными значениями.

df=df.rename(columns={'capacity': 'Number of rooms', 'stars' : 'Star rating', 
                      'dchain':'Chain affiliation', 'rating' : 'Users' rating', 
                      'Nreviewers' : 'Number of reviewers'})

df=df[['date_src', 'Number of rooms', 'Star rating', 'Chain affiliation', 
                      'Users' rating', 'Number of reviewers', 'breakfast', 
                      'freecanc', 'eurP', 'lprice100', 'panelid1415',  
                      'region', 'bdays', 'sample_mac_sr', 'hot_size', 
                      'google_src', 'town_avail', 'treat', 'Post']].dropna()

df['Postlaw_Treated']=df['Post']df['treat']

Перейдем к построению моделей на панельных данных. Начнем с объединенного МНК (pooled OLS) - обычного МНК, который не учитывает панельную структуру данных, по следующей формуле:

Y_int =β₀ +β∗X_int +ε_int, где Y_int - цена i-того отеля n-го номера, X_int - характеристики i-того отеля n-го номера.

import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.iolib.summary2 import summary_col
import statsmodels.stats.outliers_influence as oi

reg= sm.OLS(df[['lprice100']], df[['Number of rooms',  'Star rating', 
            'Chain affiliation', 'Users' rating', 'Number of reviewers', 
            'breakfast', 'freecanc', 'bdays']]).fit(cov_type="HC3")
result_table= summary_col(results = reg, stars = True)
print(result_table)

Теперь перейдем к построению моделей с фиксированными эффектами. Модели с фиксированными эффектами бывают двух видов: однонаправленные и двунаправленные. Однонаправленные модели включают в себя, помимо ковариат, ненаблюдаемый неизменный во времени признак (характеристику/особенность) каждого наблюдения (в нашем случае номера в отеле)  или фиксированный эффект времени, одинаковый для всех объектов-отелей в момент времени t (в нашем случае в момент сбора данных). Формулы выглядят так:

Y_int =β₀ + β∗X_int + α_in+ ε_int, где α_in - ненаблюдаемый неизменный во времени признак номера в отеле.

Y_int =β₀ + β∗X_int + λ_t+ ε_int, λ_t - фиксированный эффект времени, одинаковый для всех объектов в момент t.

Двунаправленная модель с фиксированными эффектами включает в себя и признак объекта и эффект времени.

Y_int =β₀ +β∗X_int +α_in+ λt +ε_int

Проблема, с которой мы сталкиваемся, - признак объекта и эффект времени (так называемые фиксированные эффекты) ненаблюдаемые - оценить их мы не можем. Поэтому, чтобы избавиться от этих эффектов, прибегнем к внутригрупповому преобразованию (рассмотрим только на примере однонаправленной модели с неизменном во времени признаком):

1 шаг: Модель для периода t: Y_int =β₀ +β∗X_int +α_i +ε_it

2 шаг: Модель в средних по времени: Y_ср =β₀ + β ∗ X_ср + α + ε_ср

3 шаг: Модель после внутригруппового преобразования: (Y_ср −Y)=β∗(X_ср −X)+(ε_ср −ε)

Преобразованная модель оценивается по МНК. Внутригрупповое преобразование (3 шаг) “съедает” неизменные во времени признаки, поэтому оценить коэффициенты при них с помощью моделей с фиксированными эффектами невозможно. 

from linearmodels.panel import PanelOLS
oneway_fe=df.set_index(["panelid1415", "Postlaw_Treated"])
reg_fe1 = PanelOLS(dependent=oneway_fe['lprice100'], 
                    exog=oneway_fe[['Number of rooms', 'Star rating', 
                    'Chain affiliation', 'Users' rating', 'Number of reviewers',
                    'breakfast', 'freecanc', 'bdays']],  
                    entity_effects=True, time_effects=False, drop_absorbed=True)
reg_fe1=reg_fe1.fit(cov_type='clustered', cluster_entity=True)
reg_fe1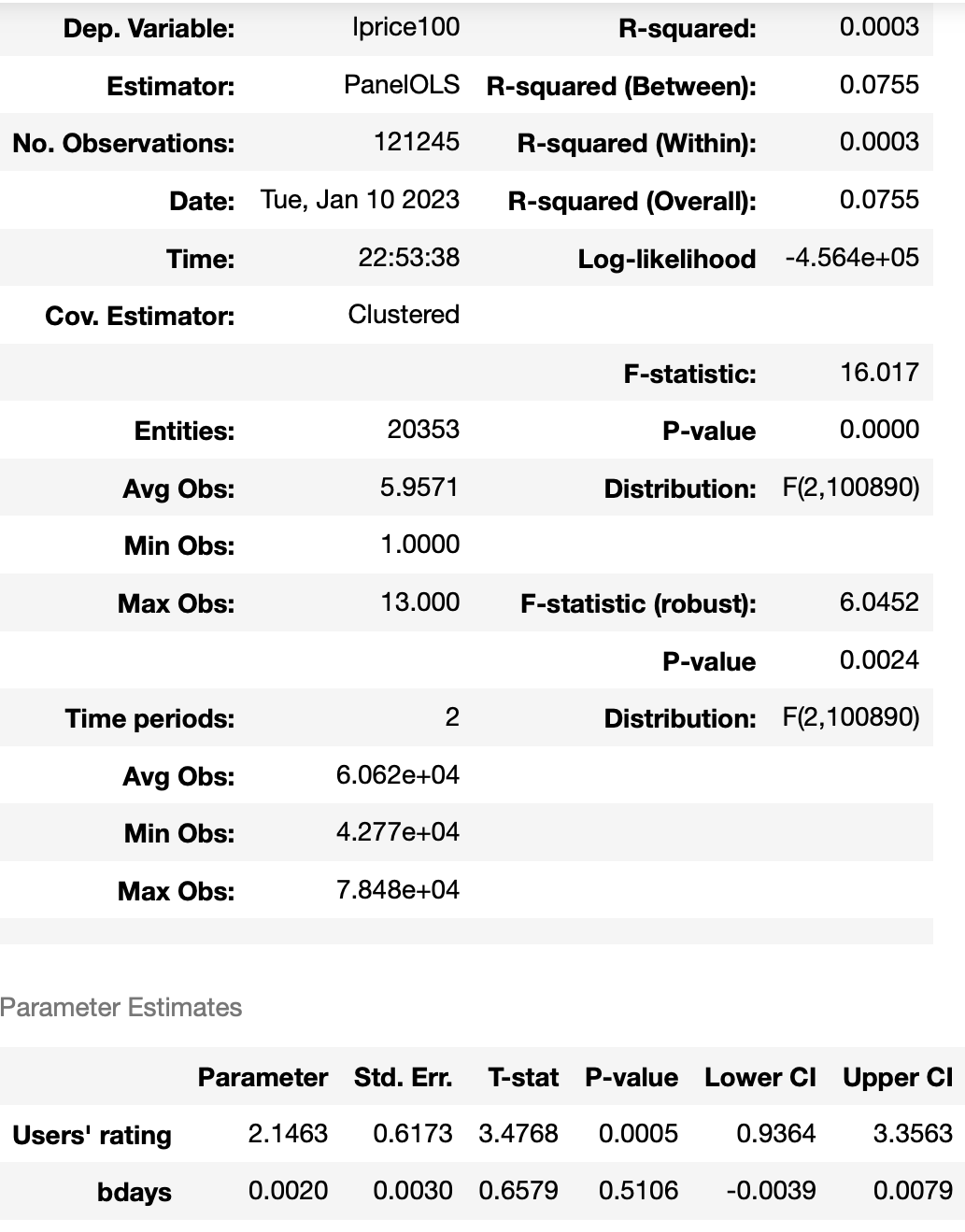

В построенной модели остались только те характеристики, которые меняются во времени.

Одной из альтернатив внутригрупповому преобразованию является обычный МНК с фиктивными переменными для каждого объекта или периода времени. В случае с номерами отелей это делать бессмысленно, так как в модели будет {количество отелей * кол-во типов номеров - 1} фиктивных переменных (напомню, что фиктивных переменных всегда n-1, где n - количество объектов, чтобы избежать мультиколлинеарности), что затруднит интерпретацию модели. Но в случае с периодами времени это сделать можно, так как зачастую периодов времени сильно меньше, чем объектов. Возьмем укрупненно - post равен 0, если момент парсинга характеристик отелей ранее введения закона Макрона, и 1, если иначе. Строим МНК-модель с фиктивной переменной времени.

reg= sm.OLS(df[['lprice100']],  df[['Post', 'Number of rooms',  'Star rating',  
            'Chain affiliation', 'Users' rating', 'Number of reviewers', 
            'breakfast', 'freecanc', 'bdays']]).fit(cov_type="HC3")
result_table= summary_col(results = reg, stars = True)
print(result_table)

А теперь построим двунаправленную модель с фиксированными эффектами.

twoway_fe=df.set_index(["panelid1415", "Postlaw_Treated"])
reg_fe2 = PanelOLS(dependent=twoway_fe['lprice100'], 
                    exog=twoway_fe[['Number of rooms', 'Star rating', 
                    'Chain affiliation', 'Users' rating', 'Number of reviewers',
                    'breakfast',  'freecanc', 'bdays']],  entity_effects=True,  
                    time_effects=True, drop_absorbed=True)
reg_fe2=reg_fe2.fit(cov_type='clustered', cluster_entity=True)
reg_fe2

Как и в случае с однонаправленной моделью с фиксированными эффектами, в двунаправленной модели с фиксированными эффектами остаются только те характеристики, которые меняются со временем.

Также на панельных данных можно построить модель со случайными эффектами: 

Y_int = β₀ + β ∗ X_int + V_int – однонаправленная модель со случайными эффектами

V_int  = μ_in + ε_int, где  μ_in - случайный эффект. Называя μ_in случайными эффектами, в прикладных исследованиях предполагают их некоррелированность с регрессорами. Фактически, v_int - особенная гетероскедастичность.

Так как регрессоры в модели со случайными эффектами некоррелированы значит они экзогенны, следовательно, параметры модели со случайными эффектами могут быть состоятельно оценены обычным МНК. Но так как МНК-оценки в модели со случайными эффектами будут состоятельными, но не эффективными, на практике модель оценивается с помощью обобщенного МНК, который позволяет получить более точные результаты (технические подробности можно посмотреть в §9.6 учебника Картаева [2]).

from linearmodels import RandomEffects
re_df=df.set_index(["panelid1415", "Postlaw_Treated"])
re=RandomEffects(dependent=re_df['lprice100'], 
                  exog=re_df[['Number of rooms',  'Star rating', 
                  'Chain affiliation', 'Users' rating', 'Number of reviewers', 
                  'breakfast', 'freecanc', 'bdays']])
re=re.fit(cov_type='clustered', cluster_entity=True)
re

Результаты построения всех моделей для сравнения приведены в таблице 1.

Таблица 1 Сравнение результатов построения моделей

Итак, мы построили несколько моделей. Теперь необходимо провести тесты, с помощью которых мы сможем выбрать лучшую модель. Схематичный выбор моделей представлен в таблице 2.

Таблица 2: Тесты для сравнения моделей, построенных на панельных данных.

Начнем с теста Чоу. Сортируем датафрейм, чтобы разделить его на две последовательные части - часть, на которую произвели воздействие, и часть, на которой не было воздействия.

df_for_chow=df.drop(columns=['panelid1415', 'region', 'date_src'])
df_for_chow=df_for_chow.sort_values(by='treat', ascending=True).reset_index().drop(columns=['index'])

for i in range (0, len(df_for_chow)):
    if df_for_chow['treat'][i]==1.0:
        break_point = i
        break

def linear_residuals(X, y):
    import pandas as pd
    import numpy as np
    from sklearn.linear_model import LinearRegression as lr

    #строим линейную модель
    model = lr().fit(X, y)

    # строим датафрейм с предсказанными значениями целевой метрики 
    summary_result = pd.DataFrame(columns = ['y_hat'])
    yhat_list = [float(i[0]) for i in np.ndarray.tolist(model.predict(X))]
    summary_result['y_hat'] = yhat_list  

    # добавляем к датафрейму реальные значения целевой метрики
    summary_result['y_actual'] = y.values

    # вычисляем остатки
    summary_result['residuals'] = summary_result.y_actual - summary_result.y_hat

    # возводим остатки в квадрат
    summary_result['residuals_sq'] = summary_result.residuals ** 2
    return(summary_result)

# пишем функцию, которая считает сумму квадратов остатков 
def calculate_RSS(X, y):
    resid_data = linear_residuals(X, y)
    rss = resid_data.residuals_sq.sum()
    return(rss)

def ChowTest(X, y, last_index_in_model_1, first_index_in_model_2):
    rss_pooled = calculate_RSS(X, y)
    # делим выборку на две подвыборке, в которой есть “слом”, наличие которого мы хотим проверить, и в котором слома нет

    X1 = X.loc[:last_index_in_model_1]
    y1 = y.loc[:last_index_in_model_1]
    rss1 = calculate_RSS(X1, y1)

    X2 = X.loc[first_index_in_model_2:]
    y2 = y.loc[first_index_in_model_2:]
    rss2 = calculate_RSS(X2, y2)

    # находим кол-во регрессоров + 1 для константы
    k = X.shape[1] + 1

    # находим кол-во наблюдений до слома
    N1 = X1.shape[0]

    # находим кол-во наблюдений после слома
    N2 = X2.shape[0]

    # вычисляем числитель для статистики Чоу
    numerator = (rss_pooled - (rss1 + rss2)) / k

    # вычисляем знаменатель для статистики Чоу
    denominator = (rss1 + rss2) / (N1 + N2 - 2 * k)

    # вычисляем статистику Чоу
    Chow_Stat = numerator / denominator
    
    # статистика Чоу имеет распределение Фишера с k и N1 + N2 - 2k степенями свободы
    from scipy.stats import f
    
    # считаю p-value
    p_value = 1 - f.cdf(Chow_Stat, dfn = 5, dfd = (N1 + N2 - 2 * k))
    result = (Chow_Stat, p_value)
    return(result)

ChowTest(y=df_for_chow[['lprice100']], X=df_for_chow[['Number of rooms',  
        'Star rating', 'Chain affiliation',  'Users' rating',  
        'Number of reviewers', 'breakfast',  'freecanc', 'bdays','treat']],  
        last_index_in_model_1=break_point-1,  
        first_index_in_model_2=break_point)[1]

P-value теста Чоу равно 0,01^(-16). Между pooled OLS и one-way time FE выбираем one-way time FE.

Теперь проведем тест Хаусмана, чтобы выбрать между моделями с фиксированными эффектами и моделью со случайными эффектами.

import numpy.linalg as la
from scipy import stats

def hausman(fe, re, changed_covariates): 

    #вычленяем коэффициенты при переменных
    b = fe.params
    B = re.params.loc[changed_covariates] 

    #находим ковариационную матрицу
    v_b = fe.cov
    v_B = re.cov[changed_covariates].loc[changed_covariates]

    #находим кол-во степеней свободы
    df = b.size

    #рассчитываем тестовую статистику
    chi2 = np.dot((b - B).T, la.inv(v_b - v_B).dot(b - B))

    #находим p-value
    pval = stats.chi2.sf(chi2, df)
    return round(chi2, 2), pval

Находим тестовую статистику и p-value для теста Хаусмана между однонаправленной моделью с фиксированными эффектами и моделью со случайными эффектами. 

hausman(reg_fe1, re, ['Users' rating', 'bdays'])
(-10586.98, 1.0)

Делаем выбор в пользу модели со случайными эффектами.

hausman(reg_fe2, re, ['Users' rating', 'bdays'])
(4862.71, 0.0)

Делаем выбор в пользу двунаправленной модели с фиксированными эффектами.

Проведем последний тест - тест Бреуша Пагана.

from statsmodels.compat import lzip
import statsmodels.stats.api as sms
names = ['p-value']
test_result = sms.het_breuschpagan(reg.resid, reg.model.exog)
print('p-value теста Бреуша-Пагана: ' + str(test_result[1]))
p-value теста Бреуша-Пагана: 0.0

Исходя из результатов теста Бреуша-Пагана, делаем выбор в пользу модели со случайными эффектами.

Из результатов всех тестов мы можем сделать следующие сравнения:

pooled OLS > one-way time FE

one-way FE > RE > two-way FE

pooled OLS > RE

В итоге выбираем двунаправленную модель с фиксированными эффектами и однонаправленную модель с фиксированным эффектом времени. Согласно результатам построения однонаправленной модели с фиксированным эффектом времени, можем сделать вывод, что в периоде после введения закона Макрона цена отелей и в Сардинии, и на Корсике увеличивается. Результаты построения двунаправленной модели с фиксированными эффектами не дают нам содержательный ответ на вопрос: как изменились цены после введения закона Макрона. 

Более содержательный ответ на поставленный вопрос можно получить, построив модель методом “разность разностей”. Подробнее в части 2.

Скачать код можно тут.

Список литературы:

[1] Andrea Mantovani, Claudio A. Piga, Carlo Reggiani, Online platform price parity clauses: Evidence from the EU Booking.com case, European Economic Review, Volume 131, 2021, 103625, ISSN 0014-2921, https://doi.org/10.1016/j.euroecorev.2020.103625.

[2] Филипп Картаев “Введение в эконометрику”: учебник. – М.: Экономический факультет МГУ имени М.В. Ломоносова, 2019. – 472 с. ISBN 978-5-906932-22-8