Построение моделей на панельных данных в Python, часть 2: метод “разность разностей” (diff-in-diff).
Привет, Хабр!
Данная статья является продолжением статьи “Построение моделей на панельных данных в Python, часть 1: объединенный МНК, модель с фиксированными эффектами, модель со случайными эффектами”. Напомню задачу: необходимо оценить, как изменились цены в отелях на островах Сардинии и Корсики после введения закона Макрона на острове Корсика.
Рассчитываем эффект воздействия методом разность разностей (diff-in-diff). Перед формальным описанием модели перечислю основные факторы, которые могут влиять на цену отеля:
специфические особенности острова, в котором расположен отель (эффект острова);
особенности различных периодов времени, например, изменение экономической конъюнктуры (временной эффект);
эффект анонса закона Макрона (тот самый эффект, который мы пытаемся оценить).
Формально можем записать так: Yist =αs +μt +δ⋅Dist +εist, где индекс i - номер отеля, индекс s - остров (Корсика или Сардиния), индекс t - момент времени (период до анонса закона Макрона или период после него). Yist - цена отелей; переменная D равна 1 в отелях, которые находились на Корсике (и соответственно, на которые распространяется закон Макрона) и равно 0 во всех остальных случаях (если отели находились в Сардинии и на них закон Макрона не распространялся). αs - эффект острова, он имеет два значения: αcontrol, если наблюдение относится к контрольной группе, т.е. к Сардинии; αtreatment, если наблюдение относится к испытуемой группе, т.е. к Корсике. μt - временной эффект. Он равен μbefore до анонса закона Макрона и μafter после анонса закона, δ — эффект воздействия анонса закона Макрона. Это тот самый эффект, который требуется оценить; εist — случайные ошибки модели.
Подробные выкладки можно посмотреть в учебнике Картаева в главе 11[2].
Метод разности разностей непосредственно связан с оценкой моделей при помощи регрессий. Так как мы располагаем панельными данными об объектах из испытуемой и контрольной групп за два периода (до и после введения закона Макрона), оценка метода разности разностей может быть получена в результате применения следующей модели:
Yit = β0 + β1 ⋅ Xi + β2 ⋅ Zt + δ ⋅ Xi ⋅ Zt + εit, где Xi — бинарная переменная, которая равна единице, если i-й отель находится на Корсике, Zt - бинарная переменная, которая равна единице для всех наблюдений, относящихся ко второму периоду (периоду после анонса закона).
Для состоятельности оценки требуется экзогенность объясняющей переменной. Если регрессор оказывается эндогенным из-за пропуска других существенных факторов, влияющих на Y, то эта проблема может быть решена включением в уравнение контрольных переменных.
Важная предпосылка метода разность разностей - параллельные претренды. Именно эта предпосылка позволяет предполагать, что за два периода t=0 и t=1 динамика Y (в нашем случае цены на отелей) в тритмент-группе, если бы она не подверглась воздействию, была бы такой же, как и динамика Y в контрольной группе. Проверим соблюдение этой предпосылки на наших данных.
Претренды показателя “средняя цена за неделю” сохраняются до вступления закона в силу сохраняются(см. Рисунок 2).
import matplotlib.pyplot as plt
trends= df.groupby(['week_number', 'region'], as_index=False).agg({'eurP': 'mean'})
trends['region'] = trends['region'].apply(lambda x: 1 if x == 'Corsica' else 0)
fig, axes = plt.subplots(figsize=(9,6), dpi=80)
plt.plot(trends[trends['region'] == 1]['week_number'], trends[trends['region'] == 1]['eurP'], label = 'о. Корсика', color = 'dodgerblue')
plt.plot(trends[trends['region'] == 0]['week_number'], trends[trends['region'] == 0]['eurP'], label = 'о. Сардиния', color = 'deepskyblue')
plt.axvline(x = 28, color = 'lightsteelblue', label = "Закон обнародовали")
plt.axvline(x = 32, color = 'slategrey', label = "Закон вступил в силу")
plt.legend()
plt.xlabel('Номер недели', fontsize=12)
plt.ylabel('Цена за 1 номер за 1 день, евро', fontsize=12)
plt.title('Тренды средней цены на Корсике и в Сардинии', fontsize=14)
plt.show()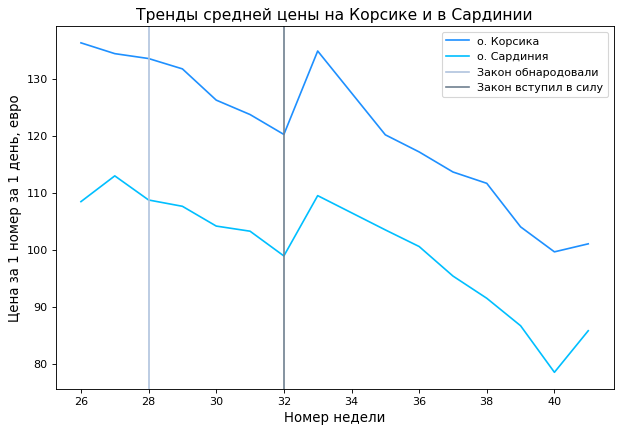
Рисунок 2: Тренды средней цены за неделю на Корсике и в Сардинии
Для построения моделей методом “разность разностей” добавим бинарные переменные.
def adding_dummies(df, col_names):
for column_name in col_names:
dummies =pd.DataFrame(pd.get_dummies(df[column_name],
prefix=column_name))
df=df.merge(dummies, left_index=True, right_index=True)
return(df)
df=adding_dummies(df, ['Star rating', 'Chain affiliation',
'hot_size', 'region'])И предобработаем данные следующим образом: если в модель мы добавим переменную PostLaw_Treated_NoChain, которая равна PostLaw* treat* Chain affiliation_0, то коэффициент при ней будет показывать насколько изменилась цена в отелях, которые “не сетевые”, на Корсике (где закон Макрона был принят) по сравнению с ценами в отелях, которые “не сетевые”, но уже в Сардинии (где закон не был принят). Введение таких новых переменных позволит нам сделать вывод об изменении цен в разрезе разных категорий.
df=df.rename(columns={'google_src': 'Google_Searchers',
'town_avail': 'Hotel_availability'})
df['Postlaw_Treated']=df['postlaw']*df['treat']
df['PostLaw_Treated_NoChain']= df['postlaw']*df['treat']*df['Chain affiliation_0']
df['PostLaw_Treated_Chain']= df['postlaw']*df['treat']*df['Chain affiliation_1']
df['PostLaw_Treated_0stars']= df['postlaw']*df['treat']*df['Star rating_0']
df['PostLaw_Treated_1stars']= df['postlaw']*df['treat']*df['Star rating_1']
df['PostLaw_Treated_2stars']= df['postlaw']*df['treat']*df['Star rating_2']
df['PostLaw_Treated_3stars']= df['postlaw']*df['treat']*df['Star rating_3']
df['PostLaw_Treated_4stars']= df['postlaw']*df['treat']*df['Star rating_4']
df['PostLaw_Treated_5stars']= df['postlaw']*df['treat']*df['Star rating_5']
df['PostLaw_Treated_small_size']= df['postlaw']*df['treat']*df['hot_size_0']
df['PostLaw_Treated_medium_size']= df['postlaw']*df['treat']*df['hot_size_1']
df['PostLaw_Treated_large_size']= df['postlaw']*df['treat']*df['hot_size_2']
df['DaysCorsica']= df['bdays']*df['region_Corsica']
df['DaysSardinia']= df['bdays']*df['region_Sardinia']
df['const']=1Строим модели. В модели добавляем контрольные переменные: количество дней с момента введения закона (DaysCorsica, DaysSardinia) для оценки долгосрочности эффекта, количество запросов в Google (Google_Searchers) и количество доступных отелей (Hotel_availability).
from linearmodels import IV2SLS
from collections import OrderedDict
from linearmodels.iv.results import compare
mod11v='lprice100 ~ Postlaw_Treated + DaysCorsica + DaysSardinia + Google_Searchers + Hotel_availability - 1'
reg11v = IV2SLS.from_formula(mod11v,df).fit(cov_type="robust")
mod22v='lprice100 ~ PostLaw_Treated_NoChain + PostLaw_Treated_Chain + DaysCorsica + DaysSardinia + Google_Searchers + Hotel_availability - 1'
reg22v = IV2SLS.from_formula(mod22v,df).fit(cov_type="robust")
mod33v='lprice100 ~ PostLaw_Treated_0stars + PostLaw_Treated_1stars + PostLaw_Treated_2stars + PostLaw_Treated_3stars + PostLaw_Treated_4stars + PostLaw_Treated_5stars + DaysCorsica + DaysSardinia + Google_Searchers + Hotel_availability -1'
reg33v = IV2SLS.from_formula(mod33v,df).fit(cov_type="robust")
mod44v='lprice100 ~ PostLaw_Treated_small_size + PostLaw_Treated_medium_size + PostLaw_Treated_large_size + DaysCorsica + DaysSardinia + Google_Searchers + Hotel_availability - 1'
reg44v = IV2SLS.from_formula(mod44v,df).fit(cov_type="robust")
res1v = OrderedDict()
res1v["D-in-D"] = reg11v
res1v["Triple_Chains"] = reg22v
res1v["Triple_Stars"] = reg33v
res1v["Triple_Size"] = reg44v
result = compare(res1v, stars=True, precision='std_errors')
print(result)
Исходя из построенных моделей, мы можем сделать следующие выводы:
введение закона Макрона повышает цену отелей, так как коэффициент при Postlaw_Treated > 0. Но увеличение цены происходит только в краткосрочном периоде. С увеличением количества дней, которые прошли с момента введения закона (с 6 августа 2015 года) цена на отели снижается: коэффициенты при DaysCorsica и DaysSardinia отрицательные. Причем на Сардинии цены снижаются быстрее и краткосрочный рост цен на отели ниже, чем на Корсике, потому что коэффициент при DaysSardinia по модулю больше коэффициента при DaysCorsica.
Цены на сетевые отели выросли больше, чем цены на несетевые отели, так как коэффициент при PostLaw_Treated_Chain > коэффициента при PostLaw_Treated_NoChain.
Чем больше количество звезд у отеля, тем сильнее увеличилась цена после введения закона Макрона, кроме однозвездочных отелей - на них цена снизилась после введения закона (коэффициент при PostLaw_Treated_1stars < 0).
Результаты построения моделей методом разность разностей дали нам более содержательную интерпретацию, чем построение модели объединенного МНК, моделей с фиксированными и случайными эффектами.
Скачать код можно тут.
[1] Andrea Mantovani, Claudio A. Piga, Carlo Reggiani, Online platform price parity clauses: Evidence from the EU Booking.com case, European Economic Review, Volume 131, 2021, 103625, ISSN 0014-2921, https://doi.org/10.1016/j.euroecorev.2020.103625.
[2] Филипп Картаев “Введение в эконометрику”: учебник. – М.: Экономический факультет МГУ имени М.В. Ломоносова, 2019. – 472 с. ISBN 978-5-906932-22-8

