Здравствуйте, меня зовут Николай Стрекопытов и большую часть карьеры я работал на стыке R&D и Deep Learning и в задачах возникающих в этих нишах часто невозможно написать какие-то автотесты и не всегда понятно где вообще может быть проблема поэтому нужно визуально исследовать графики каких-то алгоритмически-заданных функций или показаний с девайса при разных параметрах, а хочется эти графики изучить в максимально детализированном варианте, что почти всегда занимает неприлично большое количество времени.

Я подумал, что можно вычислять значения функции в узлах не в порядке "перебираем каждую строчку столбца, а затем переключаемся на следующий столбец", а в каком-то более хитром порядке И выводить результат не через часы вычислений, а по мере извлечения информации, а в точках, в которых еще не была вычислена функция показывать результат интерполяции. Собственно в этой статье я хочу описать как я разработал прототип библиотеки, которая решает эту задачу и в комментариях с удовольствием вычитаю дельные замечания.

Как можно упорядочить узлы эффективнее?

Идея строится на том, что если достаточно разумно выбрать порядок узлов, то большая часть артефактов графика будет заметна уже на 30-70% вычислений, но какие есть варианты упорядочивания узлов? Далее вас ждут то ли сырые, то ли свежие идеи о том как это можно сделать, придумывал по пути, аналогов не нашел за короткий срок поиска, если кто-то что-то знает о такой задаче или близких, то я жду вас в комментариях

1. Независимо от функции

   Следующая точка максимизирует расстояния до всех уже имеющихся точек с условием принадлежности множеству (отрезок если график функции одной переменной и прямоугольник если график функции двух переменных)
   
   
   

2. В зависимости от функции

   Методов такого типа значительно больше из-за вычислительных нюансов и сегодня мы будем рассматривать подход только первого типа, но формула может быть, например, такой
   
   
   гдеприближениепостроенное на узлах
   
   то есть каждый следующий узел это точка, в которой приближение хуже всего себя ведет. Если мы делаем такой алгоритм для произвольной дифференцируемой функции, то искать следующие точки придется в лучшем случае градиентным спуском и его можно по-разному адаптировать для конкретно этой задачи, что и дает много разных методов.

Приступаем к программированию

Перебрав несколько возможных вариантов решения оптимизационной задачи (1) и желая чтобы это происходило как можно более эффективно, я заметил, что следующие точки последовательности это всегда середины отрезков, границы которых уже в последовательности, но внутри отрезка нет ни одной точки последовательности. В качестве я взял квадрат евклидовой нормы разности (для скалярного случая просто квадрат разности).

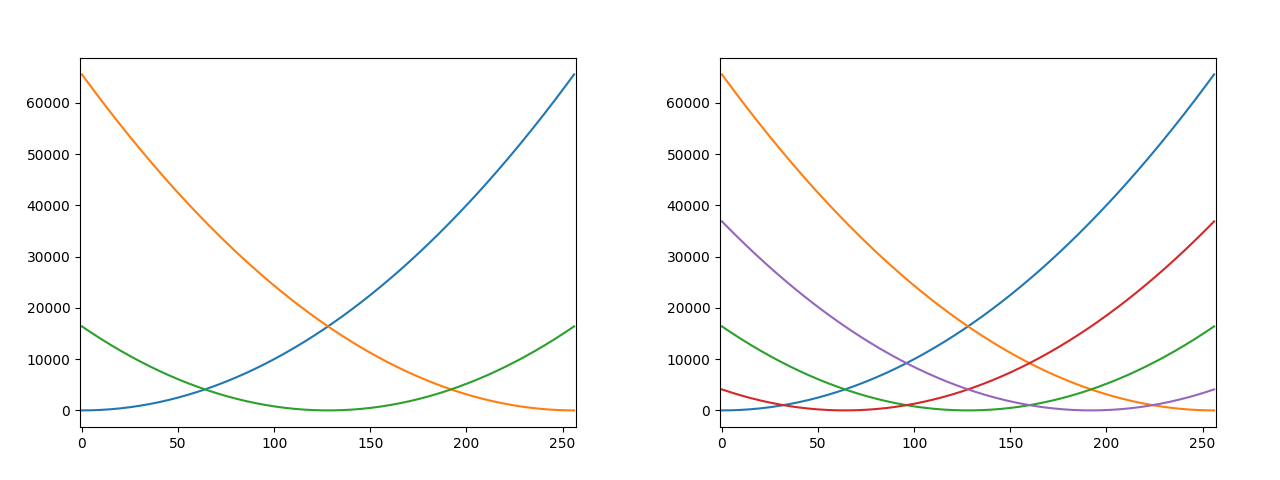
Эти точки оказались Парето-оптимальными (при изменении координат нельзя увеличить ни один из функционалов не уменьшив хотя бы один). И, что замечательно, они высчитываются без сложных оптимизационных алгоритмов, а простым усреднением некоторых пар предыдущих элементов последовательности.

Оказалось, что алгоритм оптимального упорядочивания узлов по сути является построением бинарного дерева заданной глубины.

import numpy as np

v = np.random.rand(6)

# Задаем функцию, график которой хотим исследовать. 
# Случайная частичная сумма ряда Фурье (3 первых члена)
def f(x):
  phi = np.array([np.sin(x), np.cos(x),
                 np.sin(2 * x), np.cos(2 * x),
                 np.sin(3 * x), np.cos(3 * x)])
  return np.dot(v, phi)

depth = 8 # Задаем глубину дерева или меру разрешения итогового графика

a, b = 0, 8 * np.pi # Задаем отрезок

length = 2 ** depth # Вычисляем количество узлов

x_arr = np.linspace(a, b, length) # Задаем узлы 
y_arr = np.full_like(x_arr, np.nan, dtype=np.double) # Задаем хранилище значений и заполняем nan
mask = np.full_like(x_arr, False, dtype=bool) # Задаем маску маркирующую вычисленные узлы (их индексы)

# Вычисляем на границах
y_arr[0] = f(x_arr[0])
mask[0] = True
update(x_arr[mask], y_arr[mask])

y_arr[-1] = f(x_arr[-1])
mask[-1] = True
update(x_arr[mask], y_arr[mask])

prev_nodes = [(0, -1 + 2 ** self.depth)] # Список пар узлов, в которых уже было вычислена функция и внутри отрезка которых нет точек, в которых была вычислена функция
curr_nodes = [] 

for _ in range(self.depth):

    for node in self.prev_nodes:
        c = sum(node) / 2
        curr_nodes.extend([(node[0], c), (c, node[1])])

        index = int(c)

        y_arr[index] = f(x_arr[index])
        mask[index] = True
        update(x_arr[mask], y_arr[mask])

    self.prev_nodes = list(self.curr_nodes)
    self.curr_nodes = []

Выше приведен полупсевдокод, функция update не объявлена, а она отвечает за обновление графика и интерполяцию, которая в текущей версии библиотеки полностью возложена на плечи matplotlib.Рабочий код можно посмотреть здесь github.com/nstrek/progressive_plots/

Для простоты в этой версии узлы жестко заданы и мы варьируем только порядок их вычисления, но и узлы, и их количество может задаваться алгоритмически, на основе какого-то правила. Например, количество узлов, а то есть глубину дерева можно увеличивать до тех пор пока отклонение графика с глубиной d от графика с глубиной d+1 больше чем delta.

В итоге такой алгоритм дает следующий процесс:

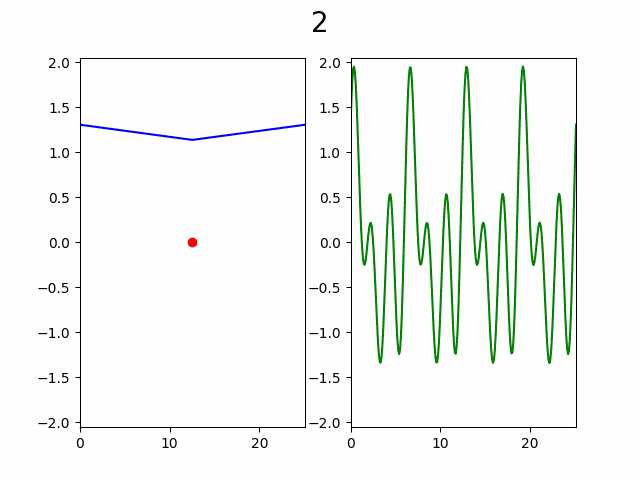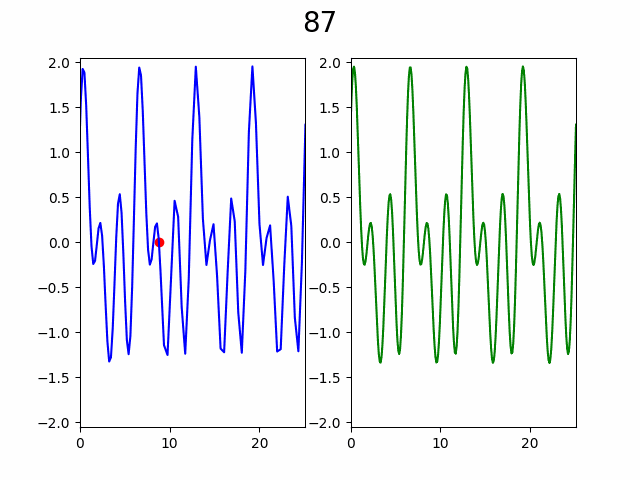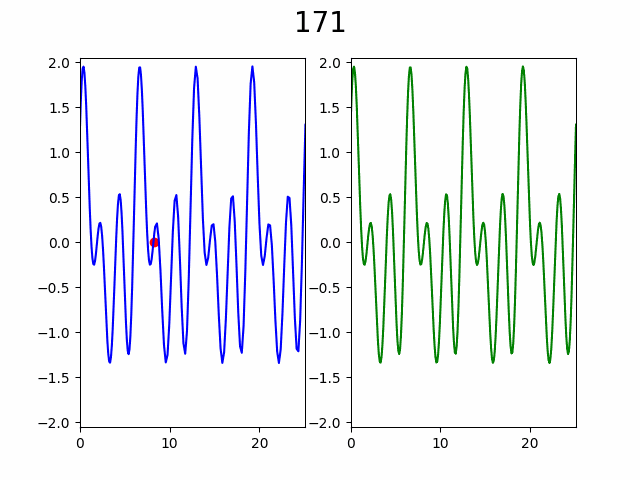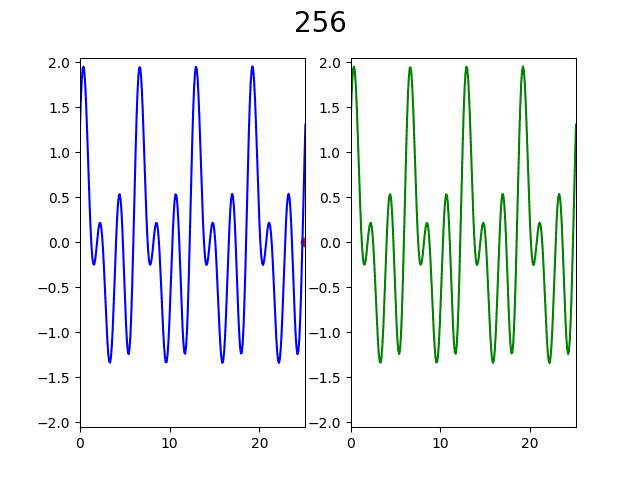
Для большей наглядности рассмотрим порядок без построения кривой:

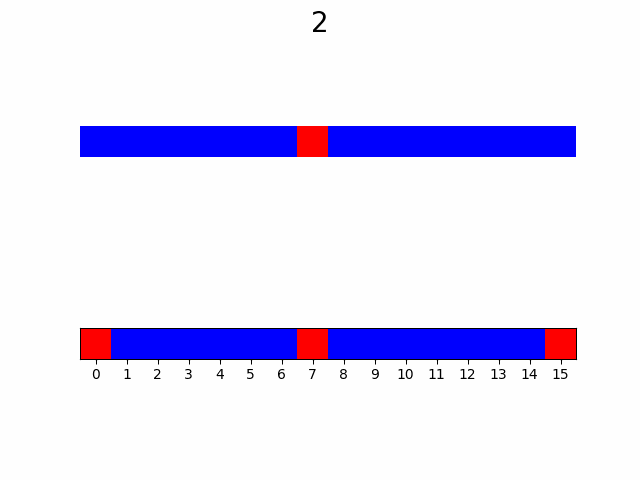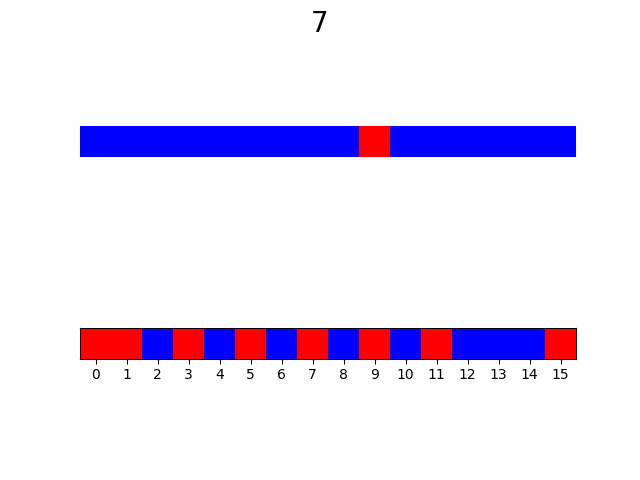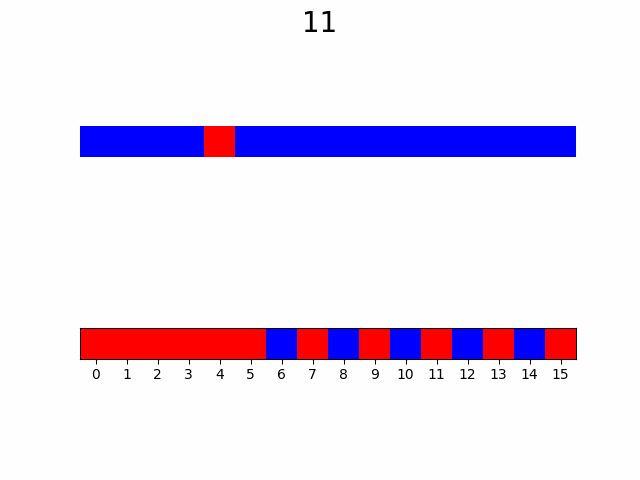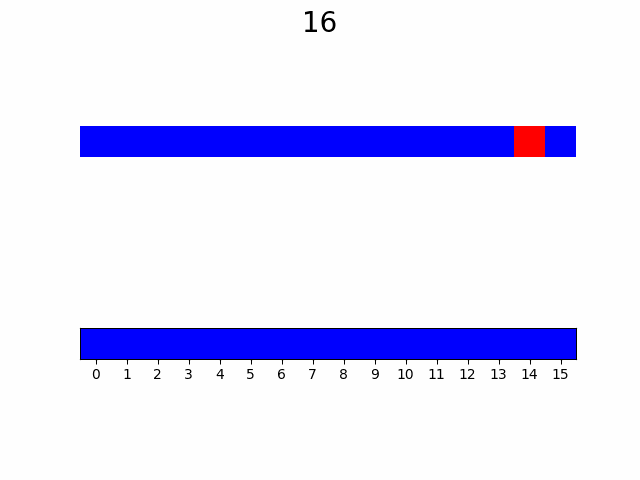
Итоги

Как видно по анимации, гипотеза подтвердилась, уже с ~50% узлов видны почти все особенности графика. Представьте насколько это внушительно если количество узлов от 10 000 и функция вычисляется хотя бы 2 секунды, а ведь при увеличении количества узла еще и доля необходимая для насыщаемости будет падать.

Жду ваши предложения и замечания в комментариях. А также приглашаю в мой блог, в котором я пишу о своих идеях и наблюдениях на стыке R&D и DL - https://t.me/research_and_deep_learning

UPD: Если вы нанимаете исследователей, то я как раз сейчас ищу работу и буду рад познакомиться