Привет, Хабр!

Меня зовут Николай Шукан, я Data Scientist и участник профессионального сообщества NTA. Сегодня речь пойдет о методах снижения размерности эмбеддингов для задач определения семантического сходства предложений.

Для чего это необходимо? С каждым годом растет сложность моделей, решающих вопросы семантически‑ и контекстно‑ориентированной обработки естественного языка (NLP). Также нельзя забывать и про проблемы мультиязычности моделей. Все это сильно сказывается на увеличении их размеров и системных требований к железу для их обучения, дообучения, да и просто запуска. Задачи NLP сегодня — это прикладные задачи, их хочется решать на доступном оборудовании и за разумное время.

А если поконкретней? Перед мной стояла задача найти и обобщить текстовые данные, представляющие собой массив предложений. Я точно знал, что среди них есть семантически схожие фразы. Однако прямой подход для определения семантического сходства наборов фраз требовал много памяти и времени. Чтобы решить эту проблему, я попытался уменьшить размерность векторов признаков предложений, но как понять, когда остановиться и что это даст?

Ну и как понять? В рамках данного поста посмотрим, как меняется оценка семантического сходства от изменения размерностей эмбеддингов разными классическими методами их уменьшения.

Введение

Мера степени семантического сходства между парами предложений — любопытный аспект NLP. Отлично справляется с группировкой схожих по смыслу предложений и предикатов, выискивает повторы, убрав которые можно снизить нагруженность модели, которая будет обрабатывать наши текстовые данные.

Для решения задачи семантического сходства между предложениями нужно преобразовать их в вектор. Для этого воспользуемся эмбеддингом: на вход подается набор предложений (в нашем случае — два для попарного сравнения), а на выходе преобразуется в числовые векторы этих предложений. Собственно, под эмбеддингом будем понимать результат преобразования текстовой сущности в числовой вектор. Модель преобразования выглядит так:

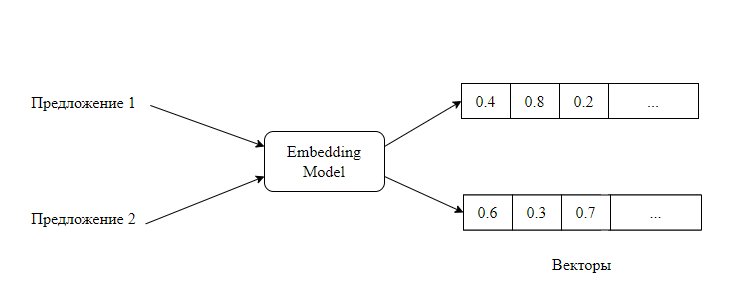
На сегодня самый простой и эффективный способ создания контекстуализированных эмбеддингов — использовать трансформер, модель машинного обучения, отлично зарекомендовавшую себя в сфере NLP.

Архитектурно трансформеры схожи с RNN (система кодировщик‑декодировщик). Кроме того, они также предназначены для обработки последовательностей. Архитектура трансформера выглядит следующим образом:

В отличие от RNN трансформеры не требуют обработки последовательностей по порядку: если входные данные это текст, то трансформеру не требуется обрабатывать конец текста после обработки его начала. Благодаря этому трансформеры распараллеливаются легче чем RNN и оттого выигрывают в скорости обучения. Также важной особенностью данной архитектуры является механизм внимания — он фокусируется на важных с точки зрения контекста словах и отдает их напрямую в обработку. Благодаря этому трансформеры обладают хорошей долгосрочной памятью и лучшим умением учитывать контекст.

Все это делает трансформеры выбором номер один для решения нашей задачи семантического сходства.

Таким образом, получим следующую модель определения семантического сходства:

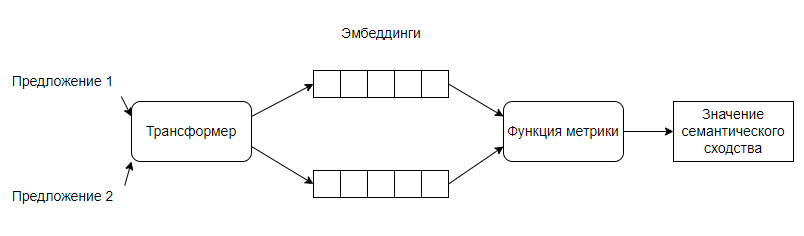
Функция метрики будет заключаться в определении близости полученных векторов. Для этого можно использовать разные инструменты, мы остановимся на косинусном сходстве:

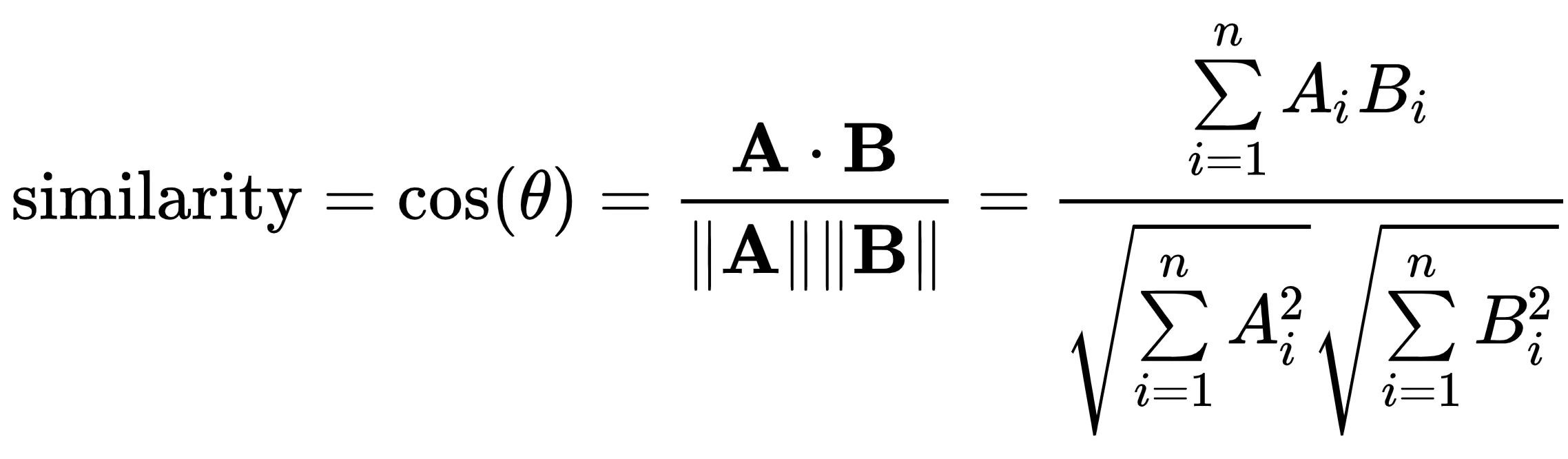
где A и B — n‑мерные вектора, θ — угол между ними, A∙B — скалярное произведение векторов A и B, ||A|| и ||B|| — длины векторов в евклидовом пространстве, A_i и B_i — i‑ые компоненты векторов A и B соответственно.

Для уменьшения количества признаков предложений, воспользуемся классическими методами снижения размерностей. Цель — уменьшить количество слабо информативных признаков для облегчения модели, но не потерять в качестве информации, т. е. получить значение семантического сходства как минимум не значительно хуже, чем до уменьшения размерности.

Схема снижения размерности будет выглядеть следующим образом:

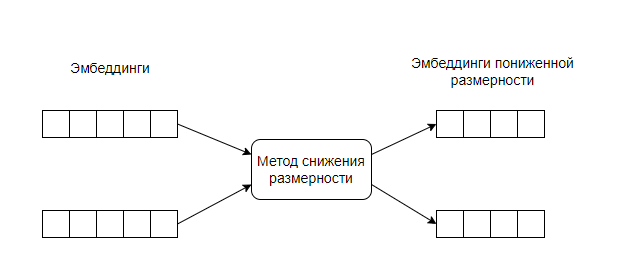
Полученные эмбеддинги пониженной размерности также отправляются на вход в функцию метрики, где уже вычисляется семантическое сходство.

Приступим к реализации описанной схемы.

В объятиях Hugging Face

Для подбора датасета и создания модели семантического сходства я обратился к замечательной платформе Hugging Face.

STSb Multi MT — это набор мультиязычных переводов и англоязычный оригинал классического STSbenchmark. Датасет состоит из трех колонок: первое предложение, второе предложение и метрика их схожести от 0 до 5 (далее — эталонная оценка). Датасет разбит на 3 части — train, test и dev. Так как в рамках поста вопросы точной донастройки рассматриваться не будет, то ограничимся dev сплитом в 1,5 тыс. строк русскоязычной части датасета.

# загрузим датасет
df_dev = load_dataset("stsb_multi_mt", name="ru", split="dev")

Первые пять строк датасета:

Среди моделей мой выбор пал на distiluse‑base‑multilingual‑cased‑v1 из семейства sentence‑transformers.

Архитектура модели выглядит следующим образом:

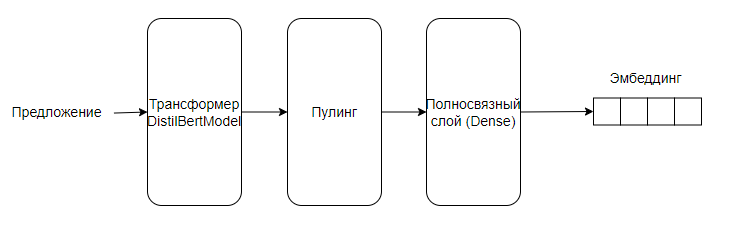
На вход в модель подается предложение. Оно проходит через слой трансформера (DistilBertModel) и преобразуется в эмбеддинг, который через слой пулинга попадает на полносвязный слой Dense с вектором смещения (bias) и тангенсальной активационной функцией. На выходе получаем эмбеддинг с размерностью 512.

Данная модель отображает предложения в 512-мерное векторное пространство.

# загрузим модель
model = SentenceTransformer("distiluse-base-multilingual-cased-v1")

Разберёмся с датасетом

Обработаем наш датасет. Для чего нормализуем эталонную оценку, приведя ее к значениям от 0 до 1. Из модели вытащим эмбеддинги и рассчитаем косинусное сходство, которое и послужит основой для сравнения с целевой метрикой датасета и измененной метрикой после снижения размерности.

res = []
F = True
for df in df_dev:
    score = float(df['similarity_score'])/5.0 # нормализация эталонной оценки
    embeddings = model.encode([df['sentence1'], df['sentence2']])
    semantic_sim = 1 - cosine(embeddings[0], embeddings[1]) # косинусное сходство между парами предложений
    res.append([df['sentence1'], df['sentence2'], score, semantic_sim])
    if F == True:
        mas_embed = embeddings
        F = False
    else:    
        mas_embed = np.concatenate((mas_embed, embeddings), axis=0)
Соберем все в единый датафрейм:
df = pd.DataFrame(res, columns=['senetence1', 'sentence2', 'score', 'semantic_sim'])

Начинаем снижение

Теперь можем приступить к применению методов снижения размерности.

Я выбрал четыре метода доступных в модуле scikit‑learn.decomposition — Матричная декомпозиция:

• PCA — Метод главных компонент.

• FastICA — Быстрый алгоритм для Анализа независимых компонент.

• Factor Analysis (FA) — Факторный анализ.

• TruncatedSVD — Усеченное сингулярное разложение.

from sklearn.decomposition import PCA
from sklearn.decomposition import FastICA
from sklearn.decomposition import FactorAnalysis
from sklearn.decomposition import TruncatedSVD

Для сравнения методов между собой и с эталонным значением воспользуемся евклидовым расстоянием:

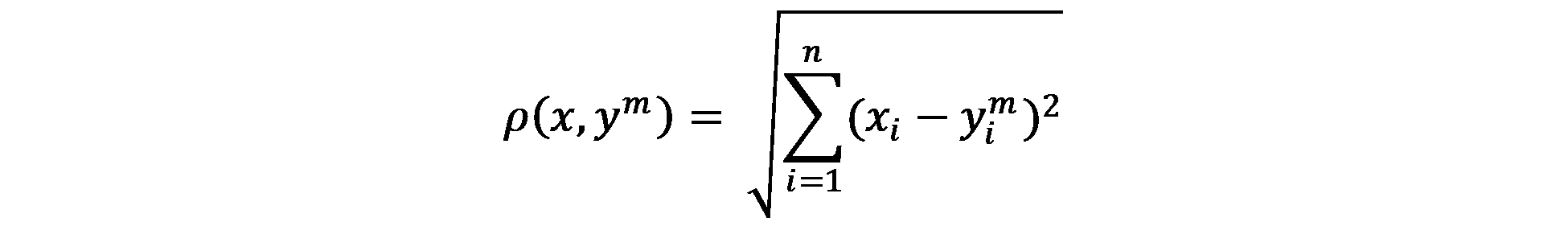
где x — вектор эталонных оценок, y^m — вектор приближений при сокращении размерности до m, n — число пар предложений, для которых надо рассчитать косинусное сходство, x_i и y_i — i‑ые элементы соответствующих векторов.

Таким образом, получим вектор эталонных оценок, основной вектор приближений (семантическое сходство), вектора приближений n‑ой размерности и i‑го метода (например, размерность 50 и метод ICA).

Приведем пример кода для метода ICA:

eucl_dis_ica = []
for el in dims:
    ica = FastICA(n_components = el)
    mas_embed_fit = ica.fit_transform(mas_embed)
    
    # семантическое сходство
    tmp_res = []
    for i in range (0, 3000, 2):
        semantic_sim = 1 - cosine(mas_embed_fit[i], mas_embed_fit[i+1])
        tmp_res.append(semantic_sim)
    
    # евклидово расстояние 
    df[f'reduce_sim_ica_{el}'] = tmp_res
    df['eucl_dis_ica'] = (df['score'] - df[f'reduce_sim_ica_{el}'])**2
    eucl_dis_ica.append(df['eucl_dis_ica'].sum() ** 0.5)

Итого, получим функцию зависимости евклидового расстояния и числа размерностей. Найдя локальный минимум евклидового расстояния до эталонной оценки на интересующем нас интервале [50; 450] размерностей, получим оптимальное количество размерностей, где нет существенных потерь информации.

Визуализируем рассчитанные данные:

plt.figure(figsize=(12,7.5), dpi= 80)
plt.plot(dims, eucl_dis_pca, color='tab:red', label='PCA')
plt.text(dims[-1], eucl_dis_pca[-1], 'PCA', fontsize=12, color='tab:red')
plt.plot(dims, eucl_dis_ica, color='tab:blue', label='ICA')
plt.text(dims[-1], eucl_dis_ica[-1], 'ICA', fontsize=12, color='tab:blue')
plt.plot(dims, eucl_dis_fa, color='tab:green', label='FA')
plt.text(dims[-1], eucl_dis_fa[-1], 'FA', fontsize=12, color='tab:green')
plt.plot(dims, eucl_dis_tsvd, color='tab:green', label='TSVD')
plt.text(dims[-1], eucl_dis_tsvd[-1], 'TSVD', fontsize=12, color='tab:green')
plt.plot(dims, targ, color='tab:orange', label='Target', linestyle='dashed')

plt.ylabel('Евклидово расстояние')
plt.xlabel('Размерность')
plt.legend(loc='upper right', ncol=2, fontsize=12)

plt.show()

Оранжевая пунктирная линия на графике (target) — это значение евклидового расстояния между вектором эталонных оценок и вектором семантического сходства (т. е. основным вектором приближения без уменьшения размерностей). С этим значением мы и будем сравнивать получившиеся функции методов снижения размерностей.

Из графика видно, что:

• Алгоритмы ICA и FA отработали лучше всего и приблизились к эталонной оценке даже больше, чем target, с локальным минимум около 200 размерностей (что в 2.5 раза меньше начальных 512).

• Алгоритм PCA показал себя чуть хуже, но при этом при 200 размерностях уже совпал с target.

• Алгоритм TSVC в чистом виде не позволяет эффективно снизить количество размерностей.

Итог

Рассмотренный алгоритм позволяет упростить модель за счет уменьшения числа избыточных, слабо информативных признаков, и это позволяет:

1. Снизить объем обрабатываемых многомерных эмбеддингов. Это также уменьшает объем задействуемой памяти и увеличивает скорость работы дальнейшей обработки этих данных. На конкретном примере сокращение объема данных составило около 60%.

2. Повысить эффективность модели. После подбора оптимального сочетания метода снижения размерности и целевого количества измерений удалось добиться сохранения качества данных и даже получить результат лучше, чем при исходных параметрах.

Посмотреть весь код можно под спойлером или на GitHub.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.spatial.distance import cosine
from sentence_transformers import SentenceTransformer
from datasets import load_dataset

# загрузим модель
model = SentenceTransformer("distiluse-base-multilingual-cased-v1")

# загрузим датасет
df_dev = load_dataset("stsb_multi_mt", name="ru", split="dev")

# конвертнем датасет в датафрейм
res = []
F = True
for df in df_dev:
    score = float(df['similarity_score'])/5.0 # нормализация эталонной оценки
    embeddings = model.encode([df['sentence1'], df['sentence2']])
    semantic_sim = 1 - cosine(embeddings[0], embeddings[1]) # косинусное сходство между парами предложений
    res.append([df['sentence1'], df['sentence2'], score, semantic_sim])
    if F == True:
        mas_embed = embeddings
        F = False
    else:    
        mas_embed = np.concatenate((mas_embed, embeddings), axis=0)

df = pd.DataFrame(res, columns=['sentence1', 'sentence2', 'score', 'semantic_sim'])
        
from sklearn.decomposition import PCA
from sklearn.decomposition import FastICA
from sklearn.decomposition import FactorAnalysis
from sklearn.decomposition import TruncatedSVD

# создадим список размерностей
dims = [x for x in range(50, 451, 50)]

# рассчитаем Евклидово расстояние для базовой модели
df['eucl_dis'] = (df['score'] - df['semantic_sim'])**2
tmp_targ = df['eucl_dis'].sum() ** 0.5
targ = [tmp_targ for _ in range(len(dims))]

# для каждого метода уменьшения размерности
# найдем эмбеддинги новых размерностей
# и для каждой пары предложений косинусное сходство
# для каждой размерности найдем евклидово расстояние до эталонной оценки 

# ICA
eucl_dis_ica = []
for el in dims:
    ica =  FastICA(n_components = el)
    mas_embed_fit = ica.fit_transform(mas_embed)
    
    # семантическое сходство
    tmp_res = []
    for i in range (0, 3000, 2):
        semantic_sim = 1 - cosine(mas_embed_fit[i], mas_embed_fit[i+1])
        tmp_res.append(semantic_sim)
    
    # евклидово расстояние 
    df[f'reduce_sim_ica_{el}'] = tmp_res
    df['eucl_dis_ica'] = (df['score'] - df[f'reduce_sim_ica_{el}'])**2
    eucl_dis_ica.append(df['eucl_dis_ica'].sum() ** 0.5)

# PCA
eucl_dis_pca = []
for el in dims:
    pca =  PCA(n_components = el)
    mas_embed_fit = pca.fit_transform(mas_embed)
    
    # семантическое сходство
    tmp_res = []
    for i in range (0, 3000, 2):
        semantic_sim = 1 - cosine(mas_embed_fit[i], mas_embed_fit[i+1])
        tmp_res.append(semantic_sim)
    
    # евклидово расстояние
    df[f'reduce_sim_pca_{el}'] = tmp_res
    df['eucl_dis_pca'] = (df['score'] - df[f'reduce_sim_pca_{el}'])**2
    eucl_dis_pca.append(df['eucl_dis_pca'].sum() ** 0.5)

# FA
eucl_dis_fa = []
for el in dims:
    fa =  FactorAnalysis(n_components = el)
    mas_embed_fit = fa.fit_transform(mas_embed)
    
    # семантическое сходство
    tmp_res = []
    for i in range (0, 3000, 2):
        semantic_sim = 1 - cosine(mas_embed_fit[i], mas_embed_fit[i+1])
        tmp_res.append(semantic_sim)
    
    # евклидово расстояние
    df[f'reduce_sim_fa_{el}'] = tmp_res
    df['eucl_dis_fa'] = (df['score'] - df[f'reduce_sim_fa_{el}'])**2
    eucl_dis_fa.append(df['eucl_dis_fa'].sum() ** 0.5)

# TSVD
eucl_dis_tsvd = []
for el in dims:
    tsvd =  TruncatedSVD(n_components = el)
    mas_embed_fit = tsvd.fit_transform(mas_embed)
    
    # семантическое сходство
    tmp_res = []
    for i in range (0, 3000, 2):
        semantic_sim = 1 - cosine(mas_embed_fit[i], mas_embed_fit[i+1])
        tmp_res.append(semantic_sim)
    
    # евклидово расстояние
    df[f'eucl_dis_tsvd_{el}'] = tmp_res
    df['eucl_dis_tsvd'] = (df['score'] - df[f'eucl_dis_tsvd_{el}'])**2
    eucl_dis_tsvd.append(df['eucl_dis_tsvd'].sum() ** 0.5)

# нарисуем график
plt.figure(figsize=(12,7.5), dpi= 80)

plt.plot(dims, eucl_dis_pca, color='tab:red', label='PCA')
plt.text(dims[-1], eucl_dis_pca[-1], 'PCA', fontsize=12, color='tab:red')
plt.plot(dims, eucl_dis_ica, color='tab:blue', label='ICA')
plt.text(dims[-1], eucl_dis_ica[-1], 'ICA', fontsize=12, color='tab:blue')
plt.plot(dims, eucl_dis_fa, color='tab:green', label='FA')
plt.text(dims[-1], eucl_dis_fa[-1], 'FA', fontsize=12, color='tab:green')
plt.plot(dims, eucl_dis_tsvd, color='tab:green', label='TSVD')
plt.text(dims[-1], eucl_dis_tsvd[-1], 'TSVD', fontsize=12, color='tab:green')
plt.plot(dims, targ, color='tab:orange', label='Target', linestyle='dashed')

plt.ylabel('Евклидово расстояние')
plt.xlabel('Размерность')

plt.legend(loc='upper right', ncol=2, fontsize=12)

plt.show()