
Автор статьи: Артем Михайлов
Привет! В последние годы аналитика данных переживает настоящий бум. Все большее количество компаний принимают решение сбора, хранения и анализа данных, чтобы повысить эффективность своих бизнес-процессов и принимать решения на основе фактов.
Одним из наиболее важных инструментов в аналитике данных является анализ временных рядов. Временной ряд - это последовательность наблюдений за определенным параметром в разные моменты времени. Таким образом, временной ряд содержит информацию о том, как изменяется параметр со временем.
Примеры временных рядов могут включать данные о продажах продукции в определенный день или данные о температуре на определенной территории в различные временные промежутки. Цель анализа временных рядов - определить закономерности в изменениях параметра во времени и сделать прогноз на будущее.
Применение анализа временных рядов может быть полезно для многих областей, включая финансы, производство, социальные и экономические исследования, климатологию и другие. Конечно, важно понимать, что в процессе анализа временных рядов возможны некоторые трудности, поэтому следует уметь применять правильные методы и инструменты для получения корректных результатов.
Таким образом, временные ряды являются одним из важных компонентов современной аналитики данных и имеет большие практические применения в различных областях. Рассмотрим основные идеи.
Обзор методов анализа временных рядов: стационарность, автокорреляция, спектральный анализ
Анализ временных рядов является важным инструментом для многих областей, в том числе бизнеса, науки, технологий и экономики. Методы анализа временных рядов помогают понять поведение и изменение временных данных и выявить скрытые тенденции и закономерности. Существует три основных метода анализа временных рядов: стационарность, автокорреляцию и спектральный анализ.
Стационарность - это свойство временного ряда, которое означает, что его средние и стандартные отклонения не меняются со временем. Если временной ряд является стационарным, то его можно легко анализировать и прогнозировать. Нестационарный временной ряд может иметь тренд (постоянный рост или падение), цикличность (повторение циклов) или сезонность (повторение определенных событий в разное время года).
Один из способов проверки стационарности временных рядов - это использование графических методов, таких как график временных рядов, график автокорреляции и график частной автокорреляции. График временного ряда позволяет визуализировать изменения значений ряда с течением времени, график автокорреляции показывает корреляцию между значениями ряда в разные периоды времени, а график частной автокорреляции учитывает корреляцию только между двумя значениями, пропуская все промежуточные значения.
Автокорреляция - это мера корреляции между значениями ряда с разницей во времени. Если временной ряд имеет высокую автокорреляцию, это означает, что значения ряда в разные периоды времени имеют сильную связь между собой. Автокорреляцию можно вычислить с помощью функции корреляции Пирсона, которая вычисляет корреляцию между двумя переменными. Для временных рядов это означает вычисление корреляции между значениями ряда в разные периоды времени. Если автокорреляция является значимой, то это может означать наличие тренда, цикличности или сезонности в ряде.

Спектральный анализ позволяет исследовать частотную составляющую ряда. Он используется для выявления скрытых цикличных паттернов во временных рядах. Для этого временной ряд разбивается на сигналы разных частот, а затем анализируется спектр этих частот. Спектральный анализ часто используется для анализа финансовых рынков, в которых цены могут изменяться в зависимости от времени и частоты.
Каждый метод имеет свои преимущества и недостатки, и их выбор зависит от конкретной области применения.
Моделирование временных рядов: авторегрессионные модели, скользящее среднее, ARIMA, SARIMA
Моделирование временных рядов является важным инструментом для прогнозирования будущих значений ряда, что позволяет принимать более обоснованные решения в различных областях.
Авторегрессионные модели (AR-модели) используют прошлые значения ряда для прогнозирования его будущих значений. Эта модель предполагает, что текущее значение ряда зависит от его предыдущих значений. Наиболее популярной AR-моделью является модель первого порядка (AR(1)), которая предполагает, что текущее значение ряда зависит только от его предыдущего значения.
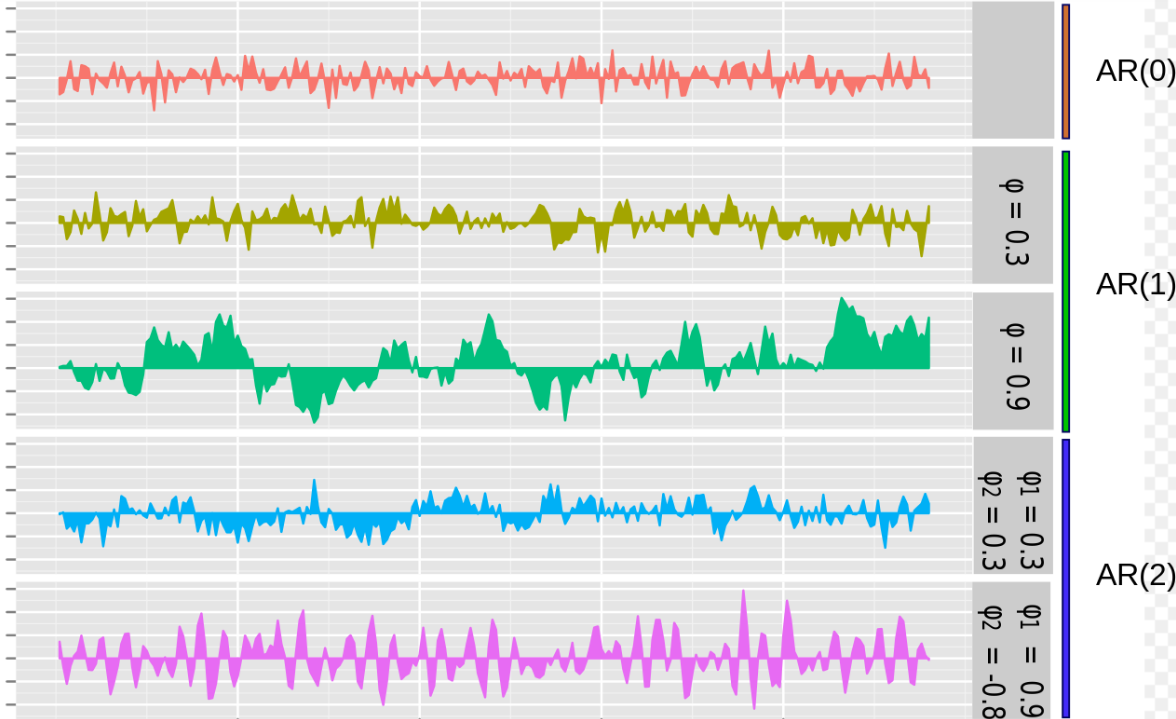
Примером использования AR-модели может служить анализ финансовых рынков. Например, с помощью AR-модели можно прогнозировать будущие цены акций на основе их прошлых значений. Если взять за основу прошлые цены и применить AR-модель, можно определить вероятные цены акций в будущем.
Следующий метод моделирования временных рядов - скользящее среднее (MA-модели). Эта модель использует прошлые значения ошибок - разницу между фактическими значениями ряда и его прогнозируемыми значениями, для прогнозирования будущих значений. Наиболее популярной MA-моделью является модель первого порядка (MA(1)), которая предполагает, что текущая ошибка зависит только от ее предыдущего значения.
Примером использования MA-модели может служить прогнозирование количества пользователей веб-сайта. Например, если предыдущие прогнозы ошиблись на определенный процент, можно использовать эту информацию в модели прогнозирования для улучшения точности прогноза количества пользователей.
ARIMA - это модель, комбинирующая авторегрессионные и скользящие средние модели. ARIMA позволяет моделировать данные, не являющиеся стационарными, как это не требуется для AR- и MA-моделей. ARIMA включает три параметра: параметр авторегрессии (р), параметр скользящего среднего (q) и параметр интегрирования (d).
Примером использования ARIMA может служить прогнозирование месячной выручки продукта на основе ежемесячных данных за прошлый год. Если прошлые данные имеют тренд, сезонность или циклы, можно использовать ARIMA для учета этих факторов в прогнозировании выручки.
SARIMA - это модель, комбинирующая ARIMA с сезонностью. SARIMA используется для моделирования сезонного поведения временных рядов. SARIMA - это расширение ARIMA с тремя дополнительными параметрами, определяющими сезонность: период сезонности (P), параметр авторегрессии со сезонностью (S) и параметр скользящего среднего со сезонностью (Q).
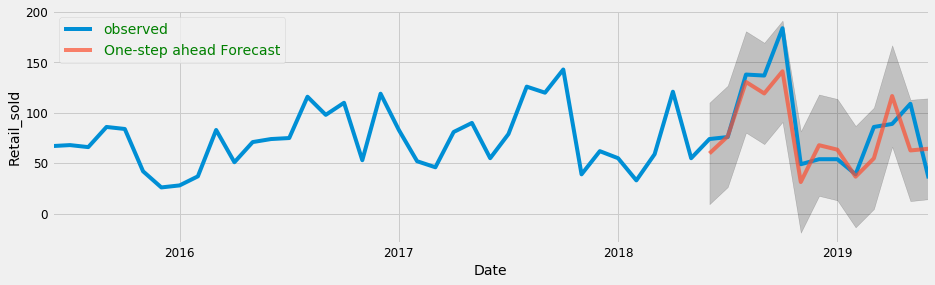
Примером использования SARIMA может служить прогнозирование продаж в интернет-магазине. Если продажи показывают сезонность, например, рост продаж в преддверии праздников, можно использовать SARIMA для прогнозирования продаж в будущих сезонах.
Прогнозирование временных рядов: методы экстраполяции, методы машинного обучения, прогнозирование с помощью SARIMA
Существует несколько методов прогнозирования временных рядов, включая методы экстраполяции, методы машинного обучения (регрессия, нейронные сети) и прогнозирование с помощью SARIMA.
Методы экстраполяции - это методы, которые используют значения предыдущих периодов для прогнозирования будущих значений ряда. Методы экстраполяции включают метод скользящего среднего, экспоненциальное сглаживание и метод Хольта-Винтерса. Метод скользящего среднего заключается в вычислении среднего значения ряда за определенный период, а затем использовании этого значения для прогнозирования будущих значений.

Экспоненциальное сглаживание использует экспоненциальную функцию для прогнозирования будущих значений, а метод Хольта-Винтерса добавляет тренд и сезонность к модели экспоненциального сглаживания.
Методы машинного обучения - это методы прогнозирования, которые используют данные прошлых значений ряда в качестве входных данных для модели обучения. Регрессия - это метод машинного обучения, который моделирует зависимость между независимыми (входными) и зависимыми (выходными) переменными. В случае прогнозирования временных рядов, независимыми переменными будут значения ряда в прошлых периодах, а зависимой переменной - будущие значения ряда. Нейронные сети - это более сложные методы машинного обучения, которые используют алгоритмы обработки информации, подобные тем, которые используют мозг. Нейронные сети могут использоваться для прогнозирования временных рядов и обычно имеют более высокую точность, чем методы экстраполяции.
Прогнозирование с помощью SARIMA - это метод прогнозирования, который использует модель SARIMA (Seasonal AutoRegressive Integrated Moving Average). Эта модель объединяет в себе методы авторегрессии, интегрированного скользящего среднего и сезонности, что позволяет прогнозировать будущие значения ряда на основе его предыдущих значений с учетом сезонных паттернов. SARIMA широко используется в экономике и финансах для прогнозирования цен на акции, индексы фондового рынка и т.д.
Примеры использования временных рядов
Приведем несколько примеров, как анализ временных рядов может использоваться для прогнозирования различных явлений в реальной жизни:
Прогнозирование трафика на дорогах. Анализ временных рядов может быть использован для прогнозирования трафика на дорогах, что поможет организовать работу служб управления трафиком и планировать дорожные ремонты. Для этого используются данных с датчиков, установленных на дорогах, анализируются трафиковые потоки в прошлом и строятся прогнозы для будущего времени. Это позволяет улучшить эффективность движения и сэкономить время путешественников.
Прогнозирование изменения погоды. Анализ временных рядов может быть также использован для прогнозирования изменений погоды. Одним из основных применений является прогнозирование температуры, осадков и других факторов, которые могут повлиять на жизнь людей и на экономику. Для этого используются данные о погоде в прошлом, а также данные о климате и других факторах, которые могут повлиять на будущие изменения погоды. Это позволяет заранее предупредить людей о возможных стихийных бедствиях и принимать соответствующие меры по их предотвращению.
Прогнозирование спроса на товар. Анализ временных рядов может быть использован для прогнозирования спроса на товары, что поможет фирмам планировать производство, закупки и продажи на рынке. Для этого используются данные о продажах товаров в прошлом, а также данные о различных факторах, которые могут повлиять на спрос в будущем (например, цены на конкурирующие товары, макроэкономические факторы).
Преимущества и недостатки
К преимуществам методов анализа и прогнозирования временных рядов можно отнести:
Позволяют оценить и выявить тенденции и цикличность временного ряда, что может привести к более точному прогнозированию будущих значений ряда;
Позволяют анализировать корреляцию между данными и выявлять зависимости между ними;
Позволяют определить влияние различных факторов на изменение ряда.
Тем не менее, методы анализа и прогнозирования временных рядов имеют и свои недостатки:
Недостаточное количество данных может существенно ограничить точность прогнозов;
Несмотря на составление относительно точных прогнозов на основе исторических данных, случайные факторы и внеплановые обстоятельства могут привести к неверному прогнозу;
Методы анализа временных рядов могут быть недостаточными, если данные обладают сезонностью и этот фактор не был учтен в анализе.
Заключение
Методы анализа временных рядов остаются крайне важными для принятия обоснованных решений в реальной жизни, и разработчики продолжают работать над дальнейшим улучшением этих методов.
В перспективе, методы анализа и прогнозирования временных рядов могут быть улучшены за счет использования более глубокого машинного обучения, например, нейронных сетей, и более точных статистических моделей, таких как модели глубокого обучения и прогнозирования с помощью SARIMA. Однако, необходимо учитывать, что точность прогнозов в зависимости от области может сильно варьироваться и требует дополнительного анализа результатов.
В конце статьи хочу порекомендовать вам бесплатный вебинар: "Аналитик и работа с проблемами и возможностями".
На занятии:
- разберете реестр методов работы с проблемами,
- определите, как аналитик может работать с проблемами и возможностями, а главное зачем это делать,
- рассмотрите, как может быть разделена ответственность между бизнес-аналитиком и системным аналитиков в этом контексте.

