«Будущее принадлежит параллельным вычислениям». MaksSun

Введение

Золотые времена подошли к концу, когда разработчикам можно было ничего не делать, а программное обеспечение работало с каждым годом все быстрее.

Распараллеливание на уровне данных. Принцип "Разделяй и властвуй".

Алгоритмы последовательных сортировок в прямом виде достаточно сложены для распараллеливания. Поэтому прибегают к стратегии «разделяй и властвуй».

Принцип «разделяй и властвуй» является одной из фундаментальных стратегий в разработке параллельных алгоритмов. Он заключается в разбиении задачи на более мелкие подзадачи, решение которых происходит независимо, а затем объединении результатов этих подзадач для получения окончательного результата.

Принцип «разделяй и властвуй» широко применяется в параллельных вычислениях, чтобы увеличить производительность и эффективность выполнения задач. Он основан на идее, что сложную задачу можно эффективно решить, разбив ее на несколько более простых подзадач, которые могут быть выполнены параллельно.

Процесс параллельного распараллеливания «разделяй и властвуй» включает следующие шаги.

1. Разделение. Исходная задача разбивается на несколько меньших и независимых подзадач. Это может быть сделано путем разделения данных, декомпозиции пространства поиска или другими методами, в зависимости от конкретной задачи.

2. Властвование. Каждая подзадача решается независимо и параллельно. Каждая подзадача может быть выполнена на своем собственном процессоре, ядре или узле в вычислительном кластере.

3. Объединение. Результаты выполнения подзадач объединяются для получения окончательного результата. Этот шаг может включать слияние данных, комбинирование результатов или другие операции, в зависимости от характера задачи.

Принцип «разделяй и властвуй» позволяет распараллелить задачи, которые имеют хорошо определенную структуру и могут быть разбиты на независимые подзадачи. Он обеспечивает возможность эффективного использования параллельных вычислительных ресурсов и ускоряет выполнение задач, особенно для больших объемов данных или вычислительно сложных алгоритмов. 

Суть метода "Разделяй и властвуй"

Программная реализация

Этап 1

Самый быстрый алгоритм (который я знаю) сортировки является "Быстрая сортировка" используем его для локальной сортировки.

// Функция для разделения массива на подмассивы с помощью опорного элемента
template <class vec, class typ>
typ partition(vec& arr, typ low, typ high) {
	using VectorType = typename std::remove_reference<decltype(arr)>::type::value_type;
	VectorType pivot = arr[high]; // Выбираем последний элемент в качестве опорного
	typ i = low - 1; // Индекс меньшего элемента

	for (typ j = low; j <= high - 1; ++j) {
		// Если текущий элемент меньше или равен опорному
		if (arr[j] <= pivot) {
			++i; // Увеличиваем индекс меньшего элемента
			std::swap(arr[i], arr[j]);
		}
	}

	std::swap(arr[i + 1], arr[high]);
	return i + 1;
}

// Рекурсивная функция для выполнения быстрой сортировки
template <class vec, class typ>
void quickSort(vec& arr, typ low, typ high) {
	if (low < high) {
		// Индекс опорного элемента после разделения
		typ pivotIndex = partition<vec, typ>(arr, low, high);

		// Рекурсивно сортируем элементы до и после опорного элемента
		quickSort<vec, typ>(arr, low, pivotIndex - 1);
		quickSort<vec, typ>(arr, pivotIndex + 1, high);
	}
}

Этап 2

Для распараллеливания используем потоки (std::thread).

// Функция разделяй и властвуй для быстрой сортировки с использованием потоков
template <class vec, class typ>
void parallelDivideAndConquerMergeSort(vec& array) {
    typ size = array.size();
    typ numThreads = std::thread::hardware_concurrency();
    typ chunkSize = size / numThreads;

    std::vector<std::thread> threads;
    for (typ i = 0; i < numThreads; ++i) {
        typ start = i * chunkSize;
        typ end = (i == numThreads - 1) ? size - 1 : start + chunkSize - 1;
        threads.emplace_back(quickSort<vec, typ>, std::ref(array), start, end);
    }

    for (auto& thread : threads) {
        thread.join();
    }

    typ step = chunkSize;
    while (step < size) {
        for (typ i = 0; i < size - step; i += 2 * step) {
            typ left = i;
            typ mid = i + step - 1;
            typ right = std::min<typ>(i + 2 * step - 1, size - 1);

            merge<vec, typ>(array, left, mid, right);
        }
        step *= 2;
    }
}

Этап 3

Функция main

int main() {
	SetConsoleCP(1251);
	SetConsoleOutputCP(1251);

	for (size_t i = 1; i <= 10; ++i)
	{
		size_t size_vector = i * (size_t)1e7;
		std::vector<int> arr(size_vector);
		std::iota(arr.begin(), arr.end(), 0);
		std::mt19937_64 urng{ 121216 };
		std::shuffle(arr.begin(), arr.end(), urng);

		auto start = std::chrono::steady_clock::now();
		//quickSort(arr, (size_t) 0, size_vector);
		parallelDivideAndConquerMergeSort<std::vector<int>, long long>(arr);
		auto end = std::chrono::steady_clock::now();

		std::cout << "Время выполнения: "
			<< std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count()
			<< " миллисекунд" << std::endl;

		if (std::is_sorted(arr.begin(), arr.end()))
			std::cout << "Массив отсортирован";
		else
			std::cout << "Не отсортирован массив";
		std::cout << std::endl;

	}

	return 1;
}

Вычислительные эксперименты

Вычисления проводились на вычислительной системе №1 (ВС №1): персональном компьютере с шестиядерным процессором AMD Ryzen 5 PRO 4400 Ггц с Radeon Graphics 3.70 GHz, 32 Гб оперативной памяти, операционная система Windows 10x64, SSD 128 Гб.

Время выполнения последовательного алгоритма Быстрой сортировки.

В таблице 1 показаны результаты последовательной быстрой сортировки (Quick sort) принципом «разделяй и властвуй», полученные на вычислительной системе № 1 (6 ядер) с использованием технологии потоков (std::thread).

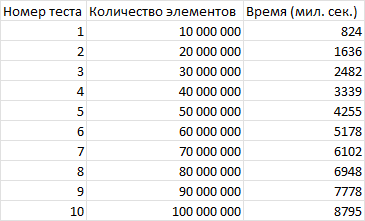
В таблице 2 показаны результаты параллельной быстрой сортировки (Quick sort) принципом «разделяй и властвуй», полученные на вычислительной системе №1 (6 ядер) с использованием технологии потоков (std::thread).

Вывод

Ускорение достигало до 5 раз включительно.

Весь код

#include <iostream>
#include <vector>
#include <random>
#include <numeric>
#include <chrono>
#include <thread>
#include <Windows.h>

// Функция для разделения массива на подмассивы с помощью опорного элемента
template <class vec, class typ>
typ partition(vec& arr, typ low, typ high) {
	using VectorType = typename std::remove_reference<decltype(arr)>::type::value_type;
	VectorType pivot = arr[high]; // Выбираем последний элемент в качестве опорного
	typ i = low - 1; // Индекс меньшего элемента

	for (typ j = low; j <= high - 1; ++j) {
		// Если текущий элемент меньше или равен опорному
		if (arr[j] <= pivot) {
			++i; // Увеличиваем индекс меньшего элемента
			std::swap(arr[i], arr[j]);
		}
	}

	std::swap(arr[i + 1], arr[high]);
	return i + 1;
}

// Рекурсивная функция для выполнения быстрой сортировки
template <class vec, class typ>
void quickSort(vec& arr, typ low, typ high) {
	if (low < high) {
		// Индекс опорного элемента после разделения
		typ pivotIndex = partition<vec, typ>(arr, low, high);

		// Рекурсивно сортируем элементы до и после опорного элемента
		quickSort<vec, typ>(arr, low, pivotIndex - 1);
		quickSort<vec, typ>(arr, pivotIndex + 1, high);
	}
}

// Функция разделяй и властвуй для сортировки слиянием с использованием потоков
template <class vec, class typ>
void parallelDivideAndConquerMergeSort(vec& array)
{
	typ size = array.size();
	typ numThreads = std::thread::hardware_concurrency();
	typ chunkSize = size / numThreads;

	std::vector<std::thread> threads;
	for (typ i = 0; i < numThreads; ++i) {
		typ start = i * chunkSize;
		typ end = (i == numThreads - 1) ? size - 1 : start + chunkSize - 1;
		threads.emplace_back(quickSort<vec, typ>, std::ref(array), start, end);
	}

	for (auto& thread : threads) {
		thread.join();
	}

	typ step = chunkSize;
	while (step < size) {
		for (typ i = 0; i < size - step; i += 2 * step) {
			typ left = i;
			typ mid = i + step;
			typ right = std::min<typ>(i + 2 * step, size);

			std::inplace_merge(array.begin() + left, array.begin() + mid, array.begin() + right);
		}
		step *= 2;
	}
}

int main() {
	SetConsoleCP(1251);
	SetConsoleOutputCP(1251);

	for (size_t i = 1; i <= 10; ++i)
	{
		size_t size_vector = i * (size_t)1e7;
		std::vector<int> arr(size_vector);
		std::iota(arr.begin(), arr.end(), 0);
		std::mt19937_64 urng{ 121216 };
		std::shuffle(arr.begin(), arr.end(), urng);

		auto start = std::chrono::steady_clock::now();
		//quickSort(arr, (size_t) 0, size_vector);
		parallelDivideAndConquerMergeSort<std::vector<int>, long long>(arr);
		auto end = std::chrono::steady_clock::now();

		std::cout << "Время выполнения: "
			<< std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count()
			<< " миллисекунд" << std::endl;

		if (std::is_sorted(arr.begin(), arr.end()))
			std::cout << "Массив отсортирован";
		else
			std::cout << "Не отсортирован массив";
		std::cout << std::endl;

	}

	return 0;
}