Как аугментация помогает нейронным сетям решать уравнения в частных производных / forpes.ru

Главная
Как аугментация помогает нейронным сетям решать уравнения в частных производных

Как аугментация помогает нейронным сетям решать уравнения в частных производных +12

11.08.2023 10:03

arudikov 25 2200 Источник

Меня зовут Александр Рудиков, я младший научный сотрудник Сколтеха. Я работаю в группе под руководством Ивана Оселедца, которая занимается решением дифференциальных уравнения с помощью нейронных сетей. Не так давно мы придумали, как сделать этот процесс точнее и доложили свои результаты на конференции ICML 2023, по итогам которой была опубликована статья в сборнике трудов. В этом тексте я хотел бы поделиться нашими наработками и подробнее рассказать, что именно мы сделали.

Введение

Обширные явления реального мира, такие как турбулентность, атмосферная циркуляция и напряжение деформируемых материалов и т.д., описываются лежащими в их основе дифференциальными уравнениями в частных производных (PDEs). Следовательно, решение PDEs является общей фундаментальной проблемой для многих научных и инженерных областей и может принести дальнейшую пользу важным приложениям реального мира. Например, моделирование воздушного потока для проектирования аэродинамического профиля крыла летательного аппарата, моделирование атмосферы для прогнозирования погоды, молекулярная динамика и т.д.

Традиционный подход к численному решению PDEs основан на использовании различных солверов, которые используют те или иные классические методы. Например, метод конечных элементов (FEM) или метод конечных разностей (FDM), которые решают PDEs путем дискретизации расчетной области. Однако, в этом случае точность численного решения сильно зависит от дискретизации расчетной сетки: грубые сетки работают быстро, но менее точно; мелкие — точны, но медленны. В реальных приложениях решение PDEs обычно требует очень хорошей дискретизации и, следовательно, очень сложны, времязатратны и трудоемки для традиционных солверов.

В последние несколько лет на решение этой проблемы направлены усилия ученых, занимающихся нейронными сетями (NNs). Широко известно, что NNs являются универсальными аппроксиматорами непрерывных функций. Более важным фактом является то, что NN с одним скрытым слоем может точно аппроксимировать любой нелинейный непрерывный оператор. Недавно в рамках нового направления было предложено изучение бесконечномерных операторов с помощью NNs. Нейронный оператор устраняет зависящую от сетки дискретизацию, создавая единый набор параметров NN, которые можно использовать с различными дискретизациями расчетной сетки. В этом случае мы имеем возможность передавать решения между расчетными сетками. Кроме того, нейронный оператор нужно обучить только один раз. Наконец, нейронный оператор не требует знания лежащего в основе PDE, только данные, полученные экспериментально или с помощью солверов.

Машина решает PDE. http://stock.adobe.com/

Нейронный оператор

Так ка же работает нейронный оператор? Рассмотрим простой пример параметрической краевой задачи:

$\begin{split} &\frac{d}{dx}\left(a(x) \frac{d}{dx} u(x)\right) = f(x),\\ &x\in[0, 1],\,u(0) = u(1) = 0. \end{split} \tag{1}$

Существует некоторый оператор G^†, отображающий коэффициент диффузии и правую часть a_j(x), f_j(x) в решение u_j(x), т.е. u_j = G^†(a_j, f_j). Для того, чтобы получить решение u_j используются традиционные солверы. Основная цель нейронного оператора — это построить аппроксимацию G^† путем построения параметрического отображения G_θ^_†:

$u_j \approx G(a_j, f_j, \theta^{\dagger}) = G_{\theta^{\dagger}}(a_j, f_j),$

где θ^† ∈ Θ — некоторый конечномерный вектор параметров. Если определить функционал качества как

$C~:~\mathcal{U \times U} \rightarrow \mathbb{R}, \quad u_j \in \mathcal{U},$

то искомый вектор параметров находится как

$\frac{1}{N}\sum_{j=1}^{N}C(G(a_j, f_j, \theta),~ G^{\dagger}(a_j, f_j)) \rightarrow \min_{\theta \in \Theta}.$

Другими словами, задача сводится к обыкновенному поиску минимума функции потерь.

Трудности решения PDEs с помощью нейронных операторов

Такой подход получает решение довольно быстро, но его основная трудность заключается в том, что, чтобы получить хорошую точность решения, обучающих пар наблюдений {a_j, u_j}^N_j₌₁ должно быть много. В этом случае, как уже было сказано выше, мы используем традиционный солвер, чтобы получить решения u_j, со всеми сопутствующими сложностями.

В классическом машинном обучении было предложено несколько способов, целью которых было увеличение количества данных без существенных вычислительных затрат. Следует заметить, что для задач, связанных с PDEs, методов увеличения данных без существенных вычислительных затрат очень мало. Наша команда, в которую входят специалисты из Сколтеха, ИВМ РАН и AIRI, разработала новый метод, позволяющий увеличивать набор данных для обучения нейронного оператора.

Центральной идеей предложенного подхода является принцип общей ковариантности. Он заключается в том, что физика явления не зависит от выбора системы координат. Математически, ковариантность означает, что физические поля являются геометрическими объектами с определенными законами преобразования при изменении системы координат.

В ряде случаев такие преобразования оставляют инвариантными уравнения, но в большинстве случаев сохраняется только форма уравнения. Более точно, для PDEs преобразование координат, выбранное соответствующим образом, приводит к изменению параметров задачи (например, поля проницаемости, коэффициента конвекции, начальных или граничных условий и т.д.). Мы использовали этот факт для построения вычислительно дешевой и широко применяемой стратегии увеличения данных (или аугментации), основанной на простых случайных преобразованиях системы координат.

Базовый пример аугментации для PDEs

Приведем простой пример нашего подхода для параметрической краевой задачи (1). Основное наблюдение состоит в том, что, когда известно PDEs, то можно извлечь больше информации из каждого полученного решения с помощью преобразования координат. Предположим, что y(ξ) является аналитической строго монотонной функцией: [0, 1] → [0, 1]. Используя x ≡ y(ξ) как координатное преобразование, можно переписать уравнение (1) в координатах ξ следующим образом:

$\begin{equation} \begin{split} &\frac{d\xi}{d y}\frac{d}{d\xi}\left(a(y(\xi)) \frac{d\xi}{d y}\frac{d}{d\xi} u(y(\xi))\right) = f(y(\xi)),\\ &\xi\in[0, 1],\,u(y(0)) = a,\,u(y(1)) = b. \end{split}\end{equation} \tag{2}$

Как видим, преобразованное уравнение (2) имеет ту же параметрическую форму, что и исходное (1). Как следствие, если тройка функций a(x), u(x), f(x) решает исходное уравнение (1), то тройка модифицированных функции a(y(x))dx/dy, u(y(x)), f(y(x))dy/dx также решает то же уравнение (1), где мы переименовали переменную ξ в x. Таким образом, мы можем создавать новые решения из старых с использованием гладких преобразований координат и интерполяции. Как генерировать гладкие преобразования координат?

Поскольку любая строго монотонная положительная функция, отображающая [0, 1], представляет собой правильное преобразование координат, можно использовать кумулятивные функции распределения со строго положительной плотностью вероятности. Можно придумать много параметрических семейств плотностей вероятностей. Например, используя тригонометрические ряды:

$\begin{equation} \begin{split} &p(x) = 1 + \sum_{k=1}^{N}\frac{\left(c_k \cos(2\pi k x) + d_k\sin(2\pi k x)\right)}{c_0},\\ & c_0 = \sum_{k=1}^{N}\left(\left|c_k\right| + \left|d_k\right|\right) + \beta,\,\beta>0. \end{split}\end{equation} \tag{3}$

После интегрирования получаем кумулятивную функцию распределения, которая служит преобразованием координат

$\begin{equation} y(x) = x + \sum_{k=1}^{N}\frac{\left(c_k \sin(2\pi k x) + d_k(1-\cos(2\pi k x))\right)}{2\pi k c_0}.\end{equation} \tag{4}$

Таким образом, вся процедура аугментации краевой задачи (1) может быть компактно записана как

$\begin{equation} \underset{\text{solve (1)}}{a(x), u(x), f(x)} \longrightarrow \underset{y(x) \text{ from (4)}}{a(y(x))\big/\frac{dy}{dx}, u(y(x)), f(y(x)) \frac{dy}{dx}}. \end{equation} \tag{5}$

Рисунок ниже иллюстрирует предложенный подход для одномерной задачи (1) и частного набора преобразований (5):

Первый столбец слева содержит a(x),f(x) и u(x), которые решают дифференциальное уравнение (1). Все остальные столбцы получаются путем преобразования координат.

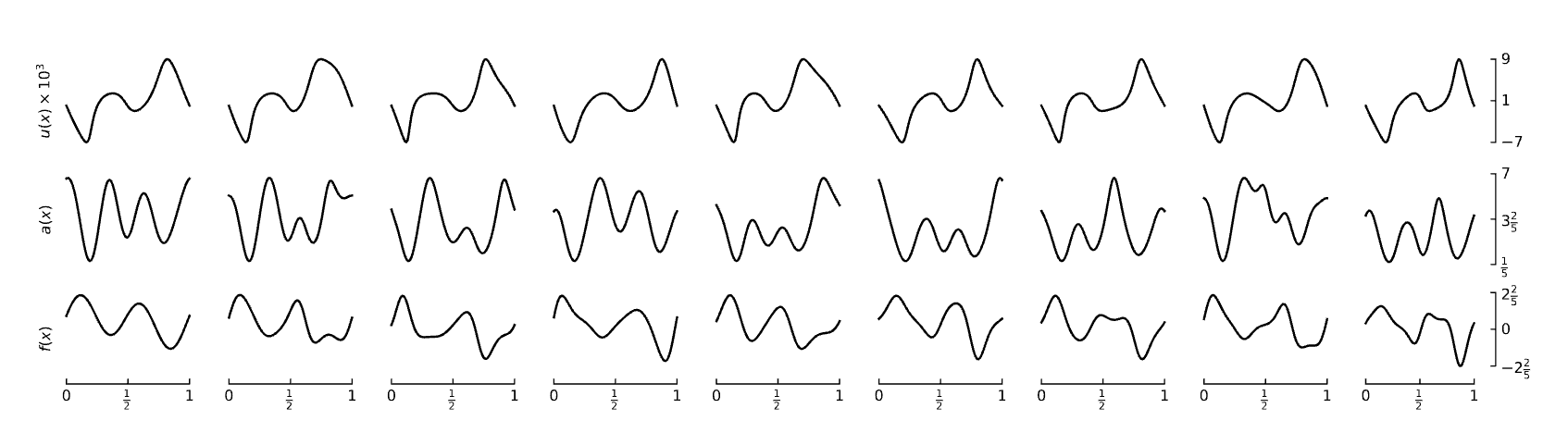
Общая стоимость таких координатных преобразований для одной пары наблюдений {a_j(x), f_j, u_j} составляет O(N), где N — количество узлов расчетной сетки. Это существенно быстрее, чем, например, решение уравнений Навье — Стокса методом конечных элементов, для которых сложность растет полиномиально.

Проверка на практике

Предложенная аугментация универсальна и может быть использована для любого нейронного оператора. Мы продемонстрировали подход на примере решения уравнения переноса, волнового уравнения, уравнения Навье — Стокса, эллиптических уравнений двух типов. В их исследования использовались следующие нейронные операторы: FNO, SNO, MLP, DilResNet, DeepONet и U-Net. Эксперименты проводились как для D = 1, так и для D = 2, где D — это количество аргументов.

Проведенные эксперименты показали, что наша аугментация позволяет ощутимо снизить ошибку обученного нейронного оператора при тестировании. Наименьшее снижение наблюдалось при работе с MLP — ошибка снизилась на 17%. Наилучший же результат был достигнут при работе с сетью DilResNet — там этот показатель вырос до 80%. В среднем по нейронным операторам и уравнениям предложенный подход сократил ошибку тестирования на 23%.

На рисунке ниже представлен результат сравнения нейронных операторов, обученных на данных с аугментацией и без нее. Степень возмущения решетки (grid distortion), полученной преобразованием системы координат, была рассчитана как максимальная разница между исходными координатами x и преобразованными x(ξ).

Зависимость ошибки предсказания от возмущения решетки при решении с помощью FNO и DilResNet с применением предложенной аугментации и без нее

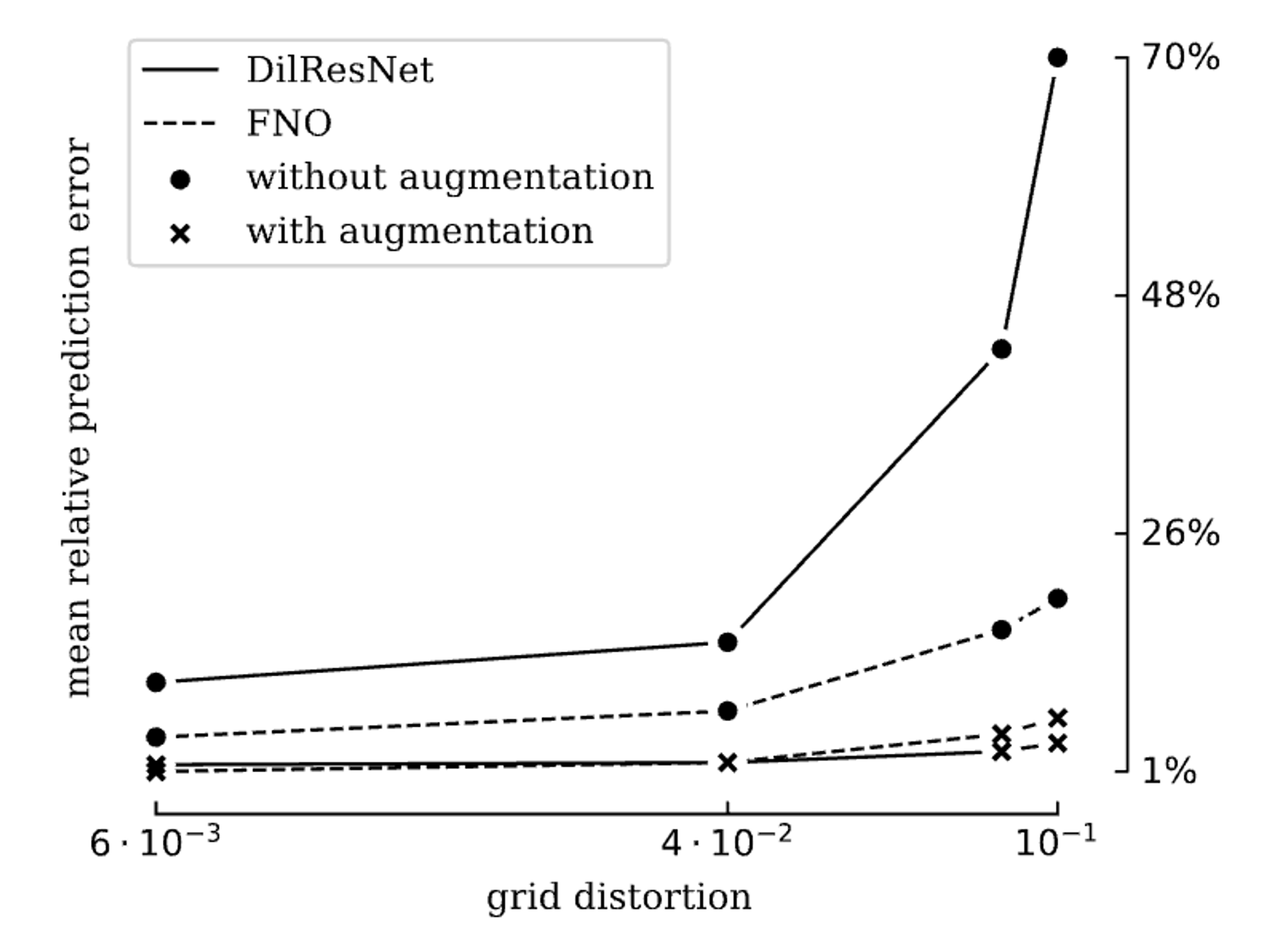
Ограничения у нашего подхода тоже имеются. Одним из них стал тот факт, что пока аугментация такого типа применима к малому набору уравнений. В дальнейшем планируется расширить круг применимости путем рассмотрения более сложных уравнений и неструктурированных сеток.

Комментарии (25)

Travisw
11.08.2023 11:32
#25848994
Так решает точно или приблизительно? Может ли она решить частные производные 2го порядка?
1. arudikov Автор
  11.08.2023 11:32
  #25849194
  +1
  Если речь идет про neural operators (FNO, SNO, DilResNet, ...), то они получают приближенное решение с достаточной степенью точности. Да, конечно, причем neural operators решают давольно большой спектр PDEs. Советую перейти по ссылкам в посте, чтобы более подробно ознакомиться.
  1. Travisw
    11.08.2023 11:32
    #25850774
    я того мнения что нейросеть решая пример 2+2 даст ответ 3.99999999999999999999999 с остальным тоже самое

berng
11.08.2023 11:32
#25849468
А зачем вам аугментация? Не проще просто фундаментальное решение один раз найти, как по классике, с дельта-функцией в правой части, а потом с любой правой частью проинтегрировать это решение? Сдается, ваша аугментация именно к этому в результате и сведется.
1. arudikov Автор
  11.08.2023 11:32
  #25850848
  +1
  Не всегда известны фундаментальные решения PDEs(например, уравнения Навье-Стокса), а если говорить про применения к прикладным задачам, где нужно решать системы PDEs, то единственным решением есть использования традиционных солверов. Neural operator - это surrogate model, и предложенный способ увеличения datasets хорошо работает в рамках этого подхода.
  1. berng
    11.08.2023 11:32
    #25851078
    +1
    Тогда я чего-то не понимаю. Вы-же тренируете сеть на экспериментальных данных? В чем смысл тренировать на экспериментальных данных схему, если можно попробовать найти общее решение (очевидно неаналитическое) или численный алгоритм для нахождения частного (как делают при численных решениях ДУ), тем более непонятно где взять столько экспериментальных данных? Просто чтобы сделать какую-то мат.модель уже известного экспериментального процесса, пригодную для каких-то расчетов, но которую нельзя будет потом обобщить на другие варианты начальных условий и непонятны будут границы ее применимости?
    
    phenik
    11.08.2023 11:32
    #25851224
    +3
    Преимущества такого подхода с использованием нейросетевых моделей, обученных на ограниченном числе симуляций или эмпирических данных, можно проиллюстрировать этой работой по расчету траекторий в задаче 3-х тел. Это особенно актуально для задач не имеющих аналитического решения, но с доступными эмпирическими данными. Не исключено, со временем, тот же сопромат ждет нейросетевая революция)
    
    berng
    11.08.2023 11:32
    #25851342
    +1
    Спасибо за ссылку, интересная работа. Но в той работе решается понятная задача - аппроксимировать результаты численного решения диффура результатами работы нейронной сети. То-есть поиск аппроксимации набора известных численных решений сложной многопараметрической функцией. А что делаете вы? Если я правильно понимаю, с экспериментом тут могут быть неконтроллируемые ошибки - одно дело известный диффур, другое дело реальный эксперимент с его ошибками и неучтенными воздействиями.
    
    А с общей идеей аугментации согласен - если вы учтете симметрию задачи аугментацией (что как я понял вы и делаете), после обучения вы должны получить аппроксимацию, инвариантную по отношению к этой симметрии. В общем для этого аугментация и используется.
    
    phenik
    11.08.2023 11:32
    #25852490
    Если я правильно понимаю, с экспериментом тут могут быть неконтроллируемые ошибки — одно дело известный диффур, другое дело реальный эксперимент с его ошибками и неучтенными воздействиями.
    
    Конечно, так же как при обучении любых нейросетей могут быть неправильно размеченные данные. Это вопрос контроля и статистики. Симуляции также делают в некоторых предположениях. Та же задача трех тел предполагает, что действием других источников гравитации можно пренебречь. В принципе можно не симулировать эти данные, а записать движение реальных небесных тел в разной конфигурации, если установить их параметры. А затем обучить сеть предсказывать траектории. Трудоемкая задача с учетом медленного движения небесных тел. Тем не менее, подобный подход к решению задач как раз актуален для астрофизических наблюдений, а объем данных от них растет астрономически) Не случайно в этой области просто взрывной рост работ по нейросетевому моделированию, здесь про некоторые проблемы, хотя это несколько другая задача, а эти публикации имеют отношению к расчету траекторий 1, 2.
    
    berng
    11.08.2023 11:32
    #25852626
    +1
    Задача физики состоит в том, чтобы выявлять закономерности и уменьшать количество неизвестных параметров, а не чтобы увеличивать их. Оккам бы перевернулся в гробу от нейросетевых выкрутасов с физикой.
    
    Это напоминает мне давний спор Птолемеевой схемы мира с Коперниковской. Как показала история, менее точная Коперниковская модель оказалась более правильной для объяснения мира, чем более точная Птолемеевская. И заменять физику на нейронку - делать шаг назад, к Птолемею.
    
    phenik
    11.08.2023 11:32
    #25853310
    Видимо не в курсе, есть такие системы которые могут выводить законы физики, например, Кеплера из эмпирических данных, см. эту публикацию. Есть целый класс "машинных ученых", которые строят сложные регрессионные модели данных (1, 2, 3 — законы Ньютона и небесной динамики, 4).
    
    В условиях наметившегося застоя в фундаментальной физике все методы хороши, включая новые. В этом коменте подробнее на эту тему, см. также другие коменты там. Вот отличный пример (статья), как нейросетевое моделирование с обучением на эмпирических данных помогает в оценке размерности сложных динамических систем. Не смотря на скепсис в коментах связанный с непривычностью подхода к решению задачи и не понимания специфики работы таких систем.
    
    Что касается уменьшения количества параметров в физических моделях, то как посмотреть. Вот неполный Лагранжиан СМ, как вам?) А теперь представьте его надо точно решить для миллиардов разных взаимодействующих частиц в реальных системах. Никакая автоматизация не поможет в этом, включая перспективные кв. технологии, только приближенные решения. Так в чем дело? Обученные нейросетевые модели как раз могут решать такие задачи, и иногда выдать решение в аналитической форме, пусть и сложных регрессий.
    
    berng
    11.08.2023 11:32
    #25853612
    +1
    Вы же сами говорите, неполный лагранжиан нужно решать точно, а потом говорите о приближенном решениии. Для приближенных методов известно что нужно оценивать расходимость, вводить критерии, проверить их еще до начала решения и т.д., чего с нейронками не всегда делается (потому-что непонятно как, в отличие от численных методов). В технических задачах - да, применение нейронных сетей полезно. А для физики нейронки - это всего-лишь модели, позволяющие какие-то задачи автоматизировать. Продвижения конекретно в теории по-моему мнению, они не дают (даже несмотря на то, что вы написали про Кеплера, читал эту статью). Экспериментаторам жизнь облегчают, сам постоянно пользуюсь.
    
    С численными решениями математики вроде лет 20-30 назад пробовали, потом перестали большинство численных решений считать за доказательство чего-бы то ни было. В физике просто до этого еще не дошли потому-что поздно начали, но фанарики уже зажигаются.
    
    Застоя в физике особо нет, есть застой с решением задач. А объяснять одну сущность миллиардом - по-моему дело наблагодарное, хотя и модное.
    
    phenik
    11.08.2023 11:32
    #25854238
    Вы же сами говорите, неполный лагранжиан нужно решать точно, а потом говорите о приближенном решениии.
    
    Как бы написал почему, из-за проблем с вычислительными ресурсами. Слишком сложно точное решение таких задач, поэтому часто применяются приближенные методы. Наглядный пример из кв. хими обсчет фолдинка биомолекул. На хабре статья была по приближенным методам решения. Сейчас это возложили на нейросеть, которая с удовлетворительной точностью решает эту задачу. Возможно и для теории выход будет по мере улучшения архитектуры сети, и набора статистики восстановления.

mikko_kukkanen
11.08.2023 11:32
#25850840
Минимизация функции ошибки - это и есть МКЭ. В статье по факту рассматриваются ОДУ. Вычислительные затраты растут как О(N), где N - количество узлов расчетной сетки. В МКЭ то же самое. Нейронная сеть - это система линейных уравнений. Ее можно решать обучением, т.е. градиентными методами, не проблема. Тоже никакой разницы с МКЭ, только возможна проблема со сходимостью. В чем все-таки преимущество предлагаемого способа?
1. arudikov Автор
  11.08.2023 11:32
  #25850868
  Для того, чтобы обучить neural operator нужно иметь некоторую выборку (параметров PDEs, решений), полученную с использование традиционных солверов. Естественно получить (очень)большую выборку теме же традиционными солверами не всегда просто как с точки зрения вычислительных ресурсов, так и с точки зрения времени. Основное преимущество предлагаемого способа заключается в том, чтобы увеличить уже существующую исходную выборку так, чтобы ошибка на тестовой выборки была как можно меньше, причем не съедая большое количество ресурсов. В статье это показана на пример как для 1D, так и для 2D.
  1. mikko_kukkanen
    11.08.2023 11:32
    #25850898
    Все-таки хочется понять алгоритм. Что Вы понимаете под терминами "выборка параметров PDE" и "выборка решений"?
    
    arudikov Автор
    11.08.2023 11:32
    #25851070
    Для примера из поста. Самый простой пример: генерируем набор {a(x), f(x)} из какого-нибудь распределения, а дальше, используя солвер, получаем решение u(x). Таким образом собираем выборку(набор наблюдений) и обучаем neural operator (FNO, SNO, ...). "Выборка параметров PDE" -- это {a_j(x), f_j(x)}, "выборка решений" -- это {u_j(x)}
    
    mikko_kukkanen
    11.08.2023 11:32
    #25851246
    И еще вопрос вдогонку. Можете пояснить, что значит "сгенерировать набор " и что за распределение имеется в виду? Можно какой-нибудь пример привести? Дальше логика вроде понятна, а в самом начале проблема.
    
    arudikov Автор
    11.08.2023 11:32
    #25851846
    Советую посмотреть статью про FNO (ссылка на статью есть в посте). Там есть пункт: Learning rate в котором написано про генерацию выборки, также внизу есть различные примеры применения.
    
    mikko_kukkanen
    11.08.2023 11:32
    #25852110
    Насчет обучающих выборок в п.з Discussion and Conclusion?
    
    lazy_val
    11.08.2023 11:32
    #25854222
    Кстати хороший вопрос - пусть нам надо решить краевую задачу для уравнения теплопроводности, у нас в идеальном газе коэффициент теплопроводности от температуры не зависит, в идеальной плазме зависит как T^(5/2). А в плазме с резким градиентом температуры поток пропорциональный этому самому градиенту получается больше чем "баллистический поток", то есть чистая беспримесная лажа. Как нам нейронная сеть поможет уравнение теплопроводности в общем виде решить?

mikko_kukkanen
11.08.2023 11:32
#25851114
Поправьте, пожалуйста, чтобы формулы проявились. Я правильно понимаю, что выборка решений - это множество (упорядоченное) функций с индексом, определяющим номер функции в выборке? Если да, то являются ли все эти функции определенными во всех точках отрезка ? Может быть, даже непрерывными при достаточно гладких (даже непрерывных?) функциях-параметрах, разумеется.
1. arudikov Автор
  11.08.2023 11:32
  #25851872
  Я правильно понимаю, что выборка решений - это множество (упорядоченное) функций с индексом, определяющим номер функции в выборке -- да. Если да, то являются ли все эти функции определенными во всех точках отрезка -- да, Может быть, даже непрерывными при достаточно гладких (даже непрерывных?) функциях-параметрах -- да, но мы также проверяем на достаточно интересных случаях(например, для эллиптического уравнения -- "ступенька").
  1. mikko_kukkanen
    11.08.2023 11:32
    #25852090
    Спасибо за ответ. Откуда вы получаете выборку непрерывных (или определенных во всех точках отрезка) решений? Насчет выборки функций - параметров предполагаю, что задаете аналитически.

lazy_val
11.08.2023 11:32
#25854208
Такой подход получает решение довольно быстро, но его основная трудность заключается в том, что, чтобы получить хорошую точность решения, обучающих пар наблюдений {aj, uj}Nj=1 должно быть много. В этом случае, как уже было сказано выше, мы используем традиционный солвер, чтобы получить решения uj, со всеми сопутствующими сложностями.

По сути вся эта деятельность сводится к интерполяции / экстраполяции решений, полученных обычными численными методами ("солверами"). А если есть работающие методы - зачем тогда нейронки? Вычислительные мощности экономить и время расчета сокращать? Не факт.

Про Навье-Стокса вообще анекдот, решения сильно нелинейных систем уравнений неустойчиво по малым (и даже бесконечно малым) отклонениям начальных и граничных условий, чтобы погоду предсказывать приходится эти начальные/граничные условия методом Монте-Карло варьировать и потом по полученной выборке решений предсказывать "вероятность осадков в HH часов MM минут XX процентов". А тут вжух и вот вам решение.

Как аугментация помогает нейронным сетям решать уравнения в частных производных +12

Введение

Нейронный оператор

Трудности решения PDEs с помощью нейронных операторов

Базовый пример аугментации для PDEs

Проверка на практике

Комментарии (25)

arudikov Автор

arudikov Автор

arudikov Автор

arudikov Автор

arudikov Автор

arudikov Автор