03.12.2015 10:38
Innotor 20 2200 Источник
В результате размышлений над особенностями стандарта IEEE754, я пришел к выводу, что многие положения, на которых основывается данный стандарт, зиждутся на ошибочном методологическом подходе. А именно, авторы стандарта за основу рассуждений взяли заданный формат машинного слова. Затем, исходя из заданного формата, были сформулированы требования к множеству чисел, которые могут быть представимы в этом формате. Было высказано ряд бездоказательных суждений. Например, о предпочтении использования в компьютерной арифметике дробной мантиссы. Или об обязательной потере точности, при представлении чисел в ненормализованном виде, а также недопустимости неоднозначного представления действительных чисел в экспоненциальном виде.

Отсюда родились требования к обязательной нормализации чисел после каждого арифметического действия, и как следствие, большие проблемы с представлением чисел, лежащих вблизи нуля, а также невозможность получения нуля в явном виде. Это все приводит к неоправданным затратам вычислительных ресурсов на нормализацию и борьбу с ее последствиями.

Предлагаемая здесь работа является логическим продолжением предыдущих двух моих топиков на Хабре. В своих рассуждениях я оттолкнулся от естественного представления чисел и ограничений, которые накладываются на числа, вследствие конечности носителя, на который они записываются. Такой подход позволил получить ряд очень важных выводов. Основной из них заключается в том, что процесс нормализации не является обязательным на всех этапах проведения арифметических операций. Более того, именно обязательная нормализация привела к необходимости введения специального класса денормализованных чисел, что существенно увеличило программно-аппаратные затраты.

Предложенный подход позволил прийти к выводу, что, добавлением всего одного разряда в машинном слове, можно в 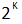раз расширить диапазон представимых чисел в формате с плавающей точкой, где К — количество разрядов машинной мантиссы.

В статье вы найдете целый ряд нетривиальных выводов, которые позволяют по-новому взглянуть на представление чисел с плавающей запятой в машинном коде.
















Комментарии (20)


  1. EjikVTumane
    03.12.2015 14:35
    #8676159
    +5

    Текст картинкой?! o_O


    1. nerudo
      03.12.2015 14:42
      #8676167
      +1

      Автор, похоже, поленился набивать формулы недружелюбным для этого средством. В целом, решение вполне здравое ;-)


    1. Uranix
      04.12.2015 12:41
      #8678563
      +2

      А чего стоят ссылки картинкой


  1. zzashpaupat
    03.12.2015 14:37
    #8676163
    +2

    А зачем вместо обычного текста, в посте картинки с текстом? Вы боитесь, что кто-то скопирует ваши измышления и выдаст за свои? Так если захотеть, то можно и картинку распознать.

    P.S. Я всегда буду обновлять комментарии перед отправкой своего.


    1. Innotor
      03.12.2015 14:41
      #8676165
      +3

      Да нет, просто мне администрация Хабра на мой вопрос, «как публиковать формулы» ответила, что только используя изображение. А поскольку формул много, в целях экономии времени, я весь текст в картинки перевел.


      1. Halt
        03.12.2015 14:42
        #8676169
        +5

        Я думаю из уважения к читателю стоило бы опубликовать материал в pdf, а пост оформить как введение и дать ссылку на скачивание. Сама тема то интересная, но подача материала мешает восприятию.


        1. Innotor
          03.12.2015 14:48
          #8676183
          +1

          Спасибо, я так и попробую сделать. Ссылку предоставлю.


      1. encyclopedist
        03.12.2015 15:00
        #8676203

        Есть онлайн-редакторы, которые позволяют это делать довольно быстро, например latex.codecogs.com/eqneditor/editor.php, или даже специализированные инструменты, как вот тут habrahabr.ru/post/263213


        1. Innotor
          03.12.2015 15:10
          #8676225

          Текст в PDF можно посмотреть по ссылке yadi.sk/i/UYfZjfNakwFoM


          1. igordata
            03.12.2015 15:29
            #8676249

            На Хабре не работает поиск ни по тексту на картинке, ни по пдфкам в ссылках.


            1. Innotor
              03.12.2015 15:38
              #8676261

              Проверил. Эта ссылка открывается yadi.sk/i/UYfZjfNakwFoM


      1. Maccimo
        04.12.2015 16:18
        #8679069

        Для формул из статьи вполне достаточно и обычного HTML и википедии: https://en.wikipedia.org/wiki/Mathematical_operators_and_symbols_in_Unicode

        Чтобы не быть голословным: http://jsfiddle.net/q9xfj9b0/


  1. Uranix
    04.12.2015 10:11
    #8678225

    По-моему логично, что работа с денормализованными числами в IEEE не сложнее работы с предлагаемыми ненормализованными числами


    1. Innotor
      04.12.2015 10:45
      #8678285

      Для программиста, с точки зрения написания кода, это видимо не сильно заметно.
      Но согласно данным, приведенным в работе. charm.cs.illinois.edu/newPapers/06-13/paper.pdf (См. TABLE II
      WORST CASE SLOWDOWNS ON OUR SUBNORMAL SLOWDOWN
      MICRO-BENCHMARK ON COMMON MICRO-ARCHITECTURES) использование денормализованных чисел существенно замедляет работу процессора. А там, где она сведена к минимуму, это достигается большими аппаратными затратами.


      1. Uranix
        04.12.2015 10:46
        #8678287

        я про реализацию на уровне железа


        1. Innotor
          04.12.2015 11:25
          #8678367

          Денормализованные, или субнормальные числа в IEEE отнесены к особому случаю и обрабатываются по особым алгоритмам. И алгоритмы эти в сопроцессоре существенно отличаются от работы с нормализованными числами.


          1. Uranix
            04.12.2015 11:38
            #8678393
            +1

            Вот, а у меня после прочтения сложилось впечатление, что вы этот алгоритм предлагаете использовать всегда.


            1. Innotor
              04.12.2015 11:43
              #8678409

              О каком алгоритме идет речь? Если не использовать специально нормализацию, то работа с нормализованными и денормализованными числами ничем не будет отличаться. Они будут обрабатываться по одним и тем же алгоритмам.


              1. Innotor
                04.12.2015 15:48
                #8679025

                Извините, я сразу не понял о каком алгоритме идет речь. В алгоритме, который я предлагаю, нет разницы между нормализованными и ненормализованными числами. Поэтому нет особого случая. Все числа обрабатываются одинаково. В том же случае, когда порядок числа по абсолютной величине превышает максимальное значение, которое может он принимать, наступает переполнение.


                1. Uranix
                  04.12.2015 16:27
                  #8679087

                  Я лишь говорю, что ваш алгоритм соответствует по сложности алгоритму работы с денормализованными числами в IEEE. В любом случае, без сравнения конкретных алгоритмов или их железной реализации, это лишь впечатление, которое может быть неверным.