На практике иногда возникает задача измерения коэффициента гармоник (Кг) генератора сигналов. Такой генератор может быть как аналоговым так и цифровым. Например, генератор на операционном усилителе, интегральном таймере (NE555), микроконтроллере (МК) или программируемой логической интегральной схеме (ПЛИС), или цифровом сигнальном процессоре (ЦСП), с выходом в виде широтно-импульсной модуляции (ШИМ) или сигналом цифро-аналогового преобразователя (ЦАП). При необходимости формирования гармонического сигнала, на выходе ШИМ или ЦАП устанавливается фильтр нижних частот (ФНЧ), который сглаживает ступенчатую форму сигнала и снижает Кг. В общем случае, измерение Кг позволяет контролировать работу как программных алгоритмов так и аппаратных узлов.
Измерить Кг можно с помощью различных приборов, например, в статье «Измерение коэффициента гармоник напряжения сигнала, заданного во временной области» приводится несколько вариантов измерения этого параметра как традиционными средствами измерений, так и перспективными. Но хочется отметить, что эти устройства более специализированные, чем, например, цифровой осциллограф или мультиметр. Поэтому, не каждый инженер или радиолюбитель отважится на покупку такого прибора.
Для того, чтобы понять как измерить Кг с помощью подручных инструментов, следует посмотреть на его формулу. Например, в статье «Коэффициент нелинейных искажений» подробно изложен физический смысл этого параметра. Простая формула, в которой используются только амплитуды гармоник сигнала. Таким образом, если измерить амплитуды гармоник сигнала на выходе генератора, то решение задачи об измерении Кг сведётся к одной формуле.
Цифровые осциллографы могут содержать опцию Fast Fourier Transform (FFT). В этом случае осциллограф переключается в режим измерения FFT, а затем с помощью маркеров, амплитуды гармоник измеряются и записываются на листочек.
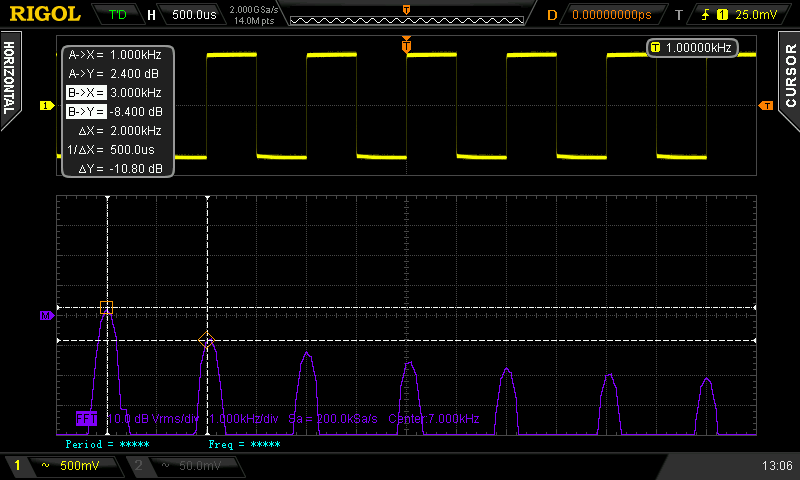
Так обычно и происходит, но во-первых — это долго, т.к. измерения производятся вручную. И, во-вторых — длительность выборки сигнала, а следовательно разрешение FFT по частоте, как правило, значительно ограничено. Другое дело, если с помощью осциллографа захватить выборку сигнала нужной длины, для последующего расчёта спектра уже на компьютере.
С захватом временной выборки сигнала и её передачей в компьютер, справятся большинство цифровых осциллографов с дистанционным интерфейсом, например, USB или Ethernet. А для расчёта Кг по спектру можно выбрать Matlab. Тем более, что при наличии Instrument Control Toolbox, дистанционный захват выборки сигнала производится прямо из Matlab.
Но прежде чем воспользоваться методом расчёта Кг по спектру, надо бы удостовериться, что осциллограф подойдёт. Согласно исследованию, с которым можно познакомиться в статье «Analytic Method for the Computation of the Total Harmonic Distortion by the Cauchy Method of Residues», Кг меандра, а также сигналов, полученных после фильтрации меандра фильтрами различных порядков, имеют определённые величины, которые в данном случае могут быть эталонами. Для проверки понадобится генератор прямоугольных импульсов, который необходимо подключить к осциллографу.

А также соответствующие фильтры, которые можно реализовать программно с помощью Signal Processing Toolbox.

Спектр выходного сигнала генератора прямоугольных импульсов. Кг = 43.98%
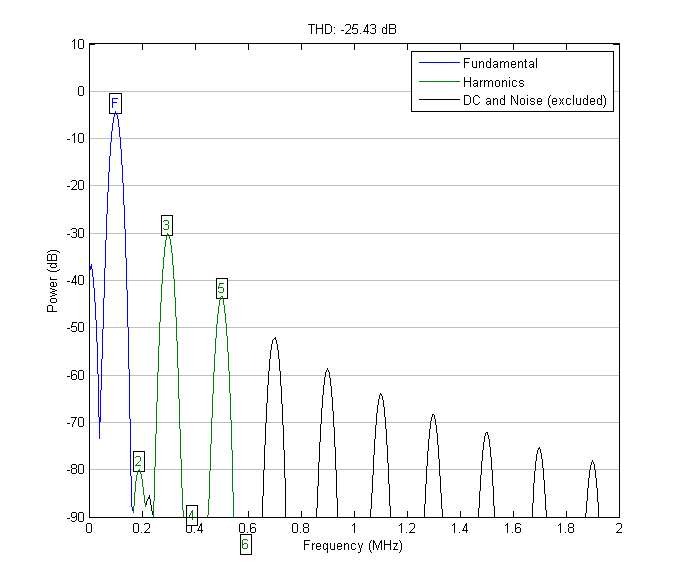
Спектр на выходе фильтра Баттерворта второго порядка. Кг = 5.36%
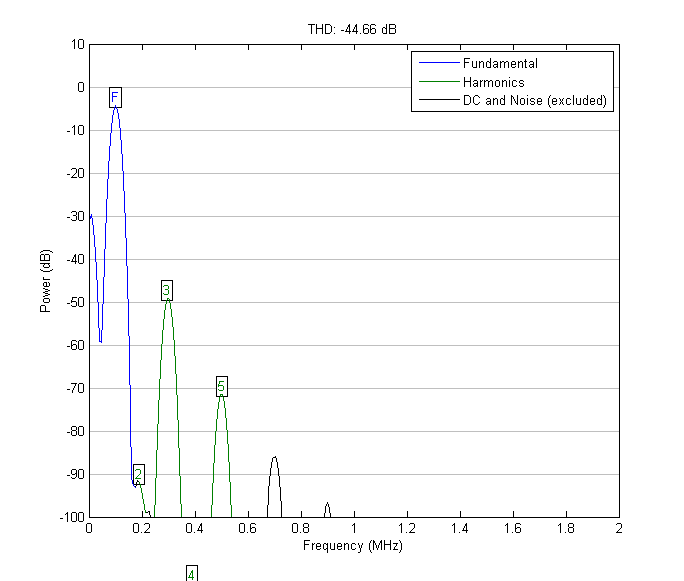
Спектр на выходе фильтра Баттерворта четвёртого порядка. Кг = 0.59%
Небольшое пояснения к графикам: логарифмические величины THD в шапках соответствуют только 5 первым гармоникам, поэтому эти величины отличаются от аналогичных, для которых предусматривается большее количество гармоник.
Стоит отметить, что Кг на выходе фильтров, полностью совпадают с расчётными. А вот Кг для прямоугольного сигнала меньше расчётного, т.к. спектр сигнала прямоугольной формы затухает медленно, и может понадобится несколько десятков гармоник для достижения расчётной величины — тут уже ничего не поделать.
Для автоматизации измерения Кг, дополнительно к предыдущему script'у, может понадобится поддержка команд испытуемого генератора с помощью Instrument Control Toolbox, но это только в том случае, если у устройства есть дистанционный интерфейс. Например, если команды реализованы как Command-line Interface (CLI), то всё должно быть просто.

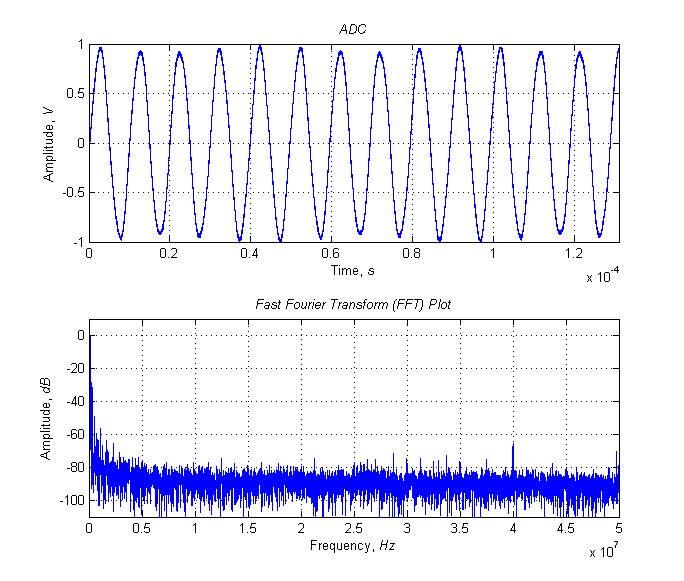
Собственно, таким образом и был измерен Кг генератора, который был разработан на базе ПЛИС, в модуле, предназначенном для проверки аналоговых систем передачи. В качестве примера, ниже приводятся графики спектров и величины Кг непосредственно на выходе ЦАП (ADC на рисунке) и после звена фильтра типа к, а также необходимый script для построения графиков.
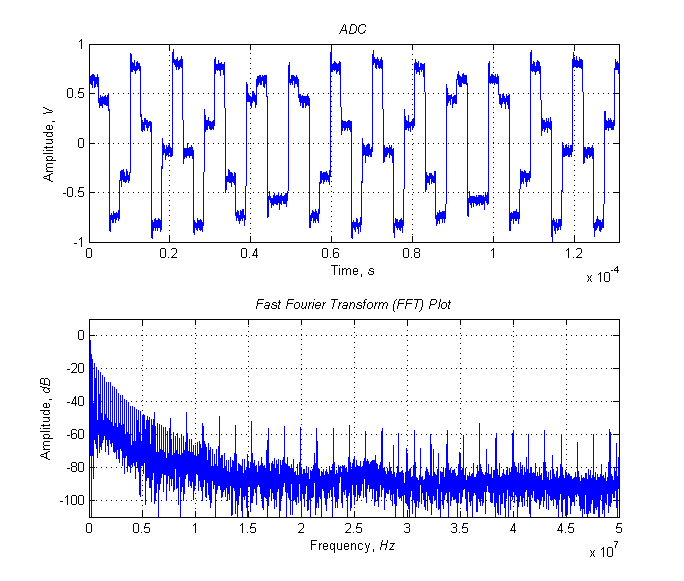
Сигнал и его спектр на выходе ЦАП, Кг = 28.3%
Сигнал и его спектр на выходе звена фильтра типа к, Кг = 2.5%
Хочется отметить, что вся эта работа была проведена только ради оценки наихудшего значения Кг максимальной частоты генератора. В рабочей полосе частот от 200Гц до 62кГц, Кг не превысил 0.34%. Для этих частот графики сигналов и спектров оказываются уже не столь интересными.
Таким образом, на примере генератора, построенного на ПЛИС с подключённым ЦАП и дополнительной фильтрацией сигнала с помощью звена ФНЧ типа к, показано, что измерение Кг в различных точках схемы можно проводить с помощью цифрового осциллографа, подключенного к компьютеру и Matlab. Такой механизм позволяет значительно сократить время на оценку качества функционирования устройства и избавляет инженера от рутины вычислений.
Измерить Кг можно с помощью различных приборов, например, в статье «Измерение коэффициента гармоник напряжения сигнала, заданного во временной области» приводится несколько вариантов измерения этого параметра как традиционными средствами измерений, так и перспективными. Но хочется отметить, что эти устройства более специализированные, чем, например, цифровой осциллограф или мультиметр. Поэтому, не каждый инженер или радиолюбитель отважится на покупку такого прибора.
Для того, чтобы понять как измерить Кг с помощью подручных инструментов, следует посмотреть на его формулу. Например, в статье «Коэффициент нелинейных искажений» подробно изложен физический смысл этого параметра. Простая формула, в которой используются только амплитуды гармоник сигнала. Таким образом, если измерить амплитуды гармоник сигнала на выходе генератора, то решение задачи об измерении Кг сведётся к одной формуле.
Цифровые осциллографы могут содержать опцию Fast Fourier Transform (FFT). В этом случае осциллограф переключается в режим измерения FFT, а затем с помощью маркеров, амплитуды гармоник измеряются и записываются на листочек.

Так обычно и происходит, но во-первых — это долго, т.к. измерения производятся вручную. И, во-вторых — длительность выборки сигнала, а следовательно разрешение FFT по частоте, как правило, значительно ограничено. Другое дело, если с помощью осциллографа захватить выборку сигнала нужной длины, для последующего расчёта спектра уже на компьютере.
С захватом временной выборки сигнала и её передачей в компьютер, справятся большинство цифровых осциллографов с дистанционным интерфейсом, например, USB или Ethernet. А для расчёта Кг по спектру можно выбрать Matlab. Тем более, что при наличии Instrument Control Toolbox, дистанционный захват выборки сигнала производится прямо из Matlab.
function [osc_data,fs] = osc_capture_ds2202()
ds2000 = visa('ni','USB0::0x1AB1::0x04B0::DS2A142900939::INSTR'); % Create VISA object.
ds2000.InputBufferSize = 2e6;
fopen(ds2000);
fprintf(ds2000,':CHAN1:BWLimit 20M'); % Set BandWidth Limit to 20MHz.
fprintf(ds2000,':ACQ:MDEPth 140000'); % Set Memory Depth from several typical values.
fs = str2double(query(ds2000,':ACQ:SRATe?')); % Get Sample Rate.
%% Setup Waveform
fprintf(ds2000,':STOP'); % Stop oscilloscope.
fprintf(ds2000,':WAV:SOURce CHAN1');
fprintf(ds2000,':WAV:MODE RAW');
fprintf(ds2000,':WAVeform:FORMat ASCII');
fprintf(ds2000,':WAV:POINts 131072'); % Number of points that must be less than MDEPth.
fprintf(ds2000,':WAV:RESet');
fprintf(ds2000,':WAV:BEGin');
pause(5); % Wait the end of the acquisition.
%% Get Waveform
while true
status = query(ds2000,':WAV:STATus?');
pause(1); % Not neccesary, but...
[state,rem] = strtok(status,',');
len = strtok(sscanf(rem,'%s'),',');
if eq(len,'0')
break;
end
if eq(state(1),'I')
osc_data = cell2mat(textscan(query(ds2000,':WAV:DATA?'),'%f','delimiter',','));
break;
else
osc_data = cell2mat(textscan(query(ds2000,':WAV:DATA?'),'%f','delimiter',','));
end
end
fprintf(ds2000,':WAV:END');
fprintf(ds2000,':RUN'); % Run the oscilloscope.
%% Delete instrument object
fclose(ds2000);
delete(ds2000);
clear ds2000;Но прежде чем воспользоваться методом расчёта Кг по спектру, надо бы удостовериться, что осциллограф подойдёт. Согласно исследованию, с которым можно познакомиться в статье «Analytic Method for the Computation of the Total Harmonic Distortion by the Cauchy Method of Residues», Кг меандра, а также сигналов, полученных после фильтрации меандра фильтрами различных порядков, имеют определённые величины, которые в данном случае могут быть эталонами. Для проверки понадобится генератор прямоугольных импульсов, который необходимо подключить к осциллографу.

А также соответствующие фильтры, которые можно реализовать программно с помощью Signal Processing Toolbox.
clear all
clc
%% Signal Acquisition
[s,fs] = osc_capture_ds2202(); % s - signal, fs - sample frequency.
%% Setup parameters
number_of_harmonics = 11; % Number of harmonics (including the fundamenal)...
% to use in the THD calculation.
L = length(s); % Length of the signal for FFT computing. It is used only for plot.
T = 1/fs;
t = (0:L-1)*T;
s_ac = s-mean(s); % Remove DC level. It is not neccesary for thd function.
s_ac = s_ac/max(abs(s_ac)); % Normalize signal. As above for thd.
%% Estimate the THD of the signal
[thd_dBc,harmpow,harmfreq] = thd(s_ac,fs,number_of_harmonics);
thd_perc = 10^(thd_dBc/20)*100 % Convert dB to Percents and display result.
figure(2);
thd(s_ac,fs); % Plot the Spectrum of the signal.
%% Apply Butterworth filter to signal and estimate THD for filtered signal
[lpFilter_b_II, lpFilter_a_II] = butter(2,2*harmfreq(1)/fs,'low'); % Design B-II filter.
filtII_s_ac = filter(lpFilter_b_II, lpFilter_a_II, s_ac); % Apply B-II filter to signal.
thd_perc_BII = 10^(thd(filtII_s_ac,fs,number_of_harmonics)/20)*100 % Convert dB to Percents and display result.
figure(3);
thd(filtII_s_ac,fs); % Plot the Spectrum of the B-II filter.
[lpFilter_b_IV, lpFilter_a_IV] = butter(4,2*harmfreq(1)/fs,'low'); % Design B-IV filter.
filtIV_s_ac = filter(lpFilter_b_IV, lpFilter_a_IV, s_ac); % Apply B-IV filter to signal.
thd_perc_BIV = 10^(thd(filtIV_s_ac,fs,number_of_harmonics)/20)*100 % Convert dB to Percents and display result.
figure(4);
thd(filtIV_s_ac,fs); % Plot the Spectrum of the B-IV filter.

Спектр выходного сигнала генератора прямоугольных импульсов. Кг = 43.98%

Спектр на выходе фильтра Баттерворта второго порядка. Кг = 5.36%

Спектр на выходе фильтра Баттерворта четвёртого порядка. Кг = 0.59%
Небольшое пояснения к графикам: логарифмические величины THD в шапках соответствуют только 5 первым гармоникам, поэтому эти величины отличаются от аналогичных, для которых предусматривается большее количество гармоник.
Стоит отметить, что Кг на выходе фильтров, полностью совпадают с расчётными. А вот Кг для прямоугольного сигнала меньше расчётного, т.к. спектр сигнала прямоугольной формы затухает медленно, и может понадобится несколько десятков гармоник для достижения расчётной величины — тут уже ничего не поделать.
Для автоматизации измерения Кг, дополнительно к предыдущему script'у, может понадобится поддержка команд испытуемого генератора с помощью Instrument Control Toolbox, но это только в том случае, если у устройства есть дистанционный интерфейс. Например, если команды реализованы как Command-line Interface (CLI), то всё должно быть просто.
[qty,b5_comport_list,~,b5] = b5_open_test; % Search connected devices.
if qty
b5.Port = b5_comport_list{1}; % Assign port to first device.
fopen(b5);
disp(b5_command(b5,'versions',.1)); % Display Versions of MCU and FPGA.
disp(b5_command(b5,'sn',.1)); % Display Serial Number.
b5_command(b5,'outrfreq 101050',.1); % Set output frequency.
b5_command(b5,'outrlvl 0',.1); % Set output level.
b5_command(b5,'outimp 600',.1); % Set output impedance.
b5_command(b5,'outpath output',.1); % Connect generator to output connector.
fclose(b5); % Close port.
delete(b5); % Clear buffer.
clear b5 % Remove var from memory.
else
disp('b5-vf is not connected');
delete(b5); % Clear buffer.
clear b5 % Remove var from memory.
end
Собственно, таким образом и был измерен Кг генератора, который был разработан на базе ПЛИС, в модуле, предназначенном для проверки аналоговых систем передачи. В качестве примера, ниже приводятся графики спектров и величины Кг непосредственно на выходе ЦАП (ADC на рисунке) и после звена фильтра типа к, а также необходимый script для построения графиков.
%% Window
win = tukeywin(length(s_ac),1); % Generate window.
% win = 1; % Disable window.
s_ac_win = s_ac.*win; % Apply the window.
%% FFT
nfft = 2^nextpow2(L); %% FFT length
fft_s_ac_win = fft(s_ac_win,nfft)/L;
f = fs/2*linspace(0,1,nfft/2+1);
win_scale = 1/mean(win); %% Normalization the result
fft_s_ac_win_lin = 2*win_scale*abs(fft_s_ac_win(1:nfft/2+1));
fft_s_ac_win_log = 20*log10(fft_s_ac_win_lin);
%% Fig 1
figure(1);
subplot(2,1,1), plot(t,s_ac), axis([0 max(t) -max(abs(s_ac)) max(abs(s_ac))]), grid on;
title('\itADC','fontsize',10);
xlabel('Time, \its','fontsize',10), ylabel('Amplitude, \itV','fontsize',10);
subplot(2,1,2), plot(f,fft_s_ac_win_log), axis([0 fs/2 -110 10]), grid on;
title('\itFast Fourier Transform (FFT) Plot','fontsize',10);
xlabel('Frequency, \itHz','fontsize',10), ylabel('Amplitude, \itdB','fontsize',10);
Сигнал и его спектр на выходе ЦАП, Кг = 28.3%

Сигнал и его спектр на выходе звена фильтра типа к, Кг = 2.5%
Хочется отметить, что вся эта работа была проведена только ради оценки наихудшего значения Кг максимальной частоты генератора. В рабочей полосе частот от 200Гц до 62кГц, Кг не превысил 0.34%. Для этих частот графики сигналов и спектров оказываются уже не столь интересными.
Таким образом, на примере генератора, построенного на ПЛИС с подключённым ЦАП и дополнительной фильтрацией сигнала с помощью звена ФНЧ типа к, показано, что измерение Кг в различных точках схемы можно проводить с помощью цифрового осциллографа, подключенного к компьютеру и Matlab. Такой механизм позволяет значительно сократить время на оценку качества функционирования устройства и избавляет инженера от рутины вычислений.
Поделиться с друзьями


AndriAnoBoTS
А собственные характеристики осциллографа вы учли? SFDR, IMD, IP3 и подобное?
sdy
Для того чтобы оценить собственные искажения осциллографа я измерил с помощью него Кг сигналов, полученных после фильтрации прямоугольного импульса. Т.е. сначала оцифровал сигнал, а потом произвёл его фильтрацию в Matlab. И сравнил результаты измерения с значениями, которые были получены аналитически. Разница Кг, полученных опытным путём и аналитически, составила сотые доли процентов. Допускаю, что это не является прямым доказательством возможности применения осциллографа для подобных измерений.
AndriAnoBoTS
А сотые доли процента для сигнала большой амплитуды дает какой уровень ошибки в абсолютных величинах? У вас на графиках я вижу измерения до уровней -80дБ(непонятно относительно чего). Сколько в дБ будут эти доли процента?
sdy
Для начала я нормализовал сигнал. И все графики построены относительно сигнала с нормализованной амплитудой. Максимальный уровень сигнала — это 0дБ. Другими словами результат не зависит от амплитуды сигнала. Но это не означает, что Кг устройства не зависит от уровня выходного сигнала. Чтобы избежать ошибки из-за зависимости Кг от амплитуды выходного сигнала, я сравнивал результаты своих измерений и результаты расчетов для сигналов с одинаковой амплитудой. В абсолютных значениях это около 1В пик-пик (1Vpp).
AndriAnoBoTS
Вопрос был не совсем про это. Даже если вы провели нормализацию сигнала(предположим по уровню первой гармоники), то сигнал остальных гармонических составляющих будет состоять из суммы сигнала искаженного исследуемым устройством и дополнительно искажениями внесенными трактом самого осциллографа. Частоты биений гармоник совпадают и Вы не можете по одному графику определить вклад каждой из составляющей(DUT и осциллографа)вы оцениваете только их сумму. Проблема в том что обычно входные цепи осциллографов не проектируются с целью минимизации гармонических искажений, после аналогового тракта ставиться АЦП c довольно низкой разрядностью 8-12 бит, и при обычном анализе сигнала (во временной форме) эти искажения не видны на экране осциллографа(при уровне гармоник -30/-40 dBFS). А отображение спектра сигнала это приятное дополнение к основному функционалу прибора. (В документации характеристики FFT никак не нормируются).
В вашем случае надо было для начала оценить уровень собственных искажений прибора для дальнейшего их учета в расчётах (хотя бы определить порядок величин).
Для этого в самом простом случае необходимо подать на вход прибора чистый синус с пиковым напряжением аналогичным напряжению с выхода генератора прямоугольных импульсов. А затем вычесть получившиеся уровни гармоник из спектра сигнала прямоугольной формы. Это не самый правильный но более менее простой способ оценки влияния самого измерительного устройства.
sdy
Да я так и хотел сделать, но чистого синуса не нашёл.
sdy
Я также согласен с тем, что полученный результат содержит Кг тракта осциллографа. Но порядок Кг тракта осциллографа существенно меньше Кг исследуемого генератора. Поэтому, я его и не учитывал. В данном случае не следует рассматривать осциллограф как средство измерения Кг.